26考研——查找_树形查找_二叉排序树(BST)(7)
408答疑
文章目录
- 三、树形查找
- 二叉排序树(BST)
- 二叉排序树中结点值之间的关系
- 二叉树形查找
- 二叉排序树的查找过程
- 示例
- 向二叉排序树中插入结点
- 插入过程
- 示例
- 构造二叉排序树的过程
- 构造示例
- 二叉排序树中删除结点的操作
- 情况一:被删除结点是叶结点
- 情况二:被删除结点只有一棵左子树或右子树
- 情况三:被删除结点有左、右两棵子树
- 二叉排序树中删除并插入某结点的分析
- 代码实操
- 结构定义
- 插入操作
- 查找操作
- 删除操作
- 中序遍历
- 六、参考资料
- 鲍鱼科技课件
- 26王道考研书
三、树形查找
二叉排序树(BST)
- 构造二叉排序树的目的并不是排序,而是提高查找、插入和删除关键字的速度,二叉排序树这种非线性结构也有利于插入和删除的实现。
- 二叉排序树(也称二叉查找树)或者是一棵空树,或者是具有下列特性的二叉树:
- 若左子树非空,则左子树上所有结点的值均小于根结点的值。
- 若右子树非空,则右子树上所有结点的值均大于根结点的值。
- 左、右子树也分别是一棵二叉排序树。
二叉排序树中结点值之间的关系
根据二叉排序树的定义,左子树结点值 < 根结点值 < 右子树结点值,因此对二叉排序树进行中序遍历,可以得到一个递增的有序序列。如下图所示二叉排序树的中序遍历序列为 123468。

二叉树形查找
- 二叉树形查找是以二叉排序树(BST)为基础进行查找,并演化出相应的平衡树AVL和红黑树RB。
- 除了掌握基础的查找,还需掌握平衡树的平衡调整过程。
二叉排序树的查找过程
二叉排序树的查找是从根结点开始,沿某个分支逐层向下比较的过程。若二叉排序树非空,先将给定值与根结点的关键字比较,若相等,则查找成功;若不等,若小于根结点的关键字,则在根结点的左子树上查找,否则在根结点的右子树上查找。这显然是一个递归的过程。
示例
如下图中查找值为 4 的结点。首先 4 与根结点 6 比较。由于 4 小于 6,所以在根结点 6 的左子树中继续查找。由于 4 大于 2,所以在结点 2 的右子树中查找,查找成功。

向二叉排序树中插入结点
二叉排序树作为一种动态树表,其特点是树的结构通常不是一次生成的,而是在查找过程中,当树中不存在关键字值等于给定值的结点时再进行插入的。
插入过程
- 若原二叉排序树为空,则直接插入;
- 否则,若关键字 k k k 小于根结点值,则插入到左子树,若关键字 k k k 大于根结点值,则插入到右子树。
- 插入的结点一定是一个新添加的叶结点,且是查找失败时的查找路径上访问的最后一个结点的左孩子或右孩子。
示例
下图展示了在一棵二叉排序树中依次插入结点 28 和结点 58 的过程,虚线表示的边是其查找的路径。

构造二叉排序树的过程
从一棵空树出发,依次输入元素,将它们插入二叉排序树中的合适位置。设查找的关键字序列为 {45, 24, 53, 45, 12, 24},则生成的二叉排序树如下图所示。
构造示例

每一步都是根据关键字与当前树中结点的比较结果,决定插入的位置。
二叉排序树中删除结点的操作
在二叉排序树中删除一个结点时,不能简单地删除该结点及其所有子结点,而是需要重新链接因删除结点而断开的二叉链表,确保二叉排序树的性质不丢失。删除操作的实现过程按以下三种情况来处理:
情况一:被删除结点是叶结点
- 若被删除结点 z z z 是叶结点,则直接删除,不会破坏二叉排序树的性质。

情况二:被删除结点只有一棵左子树或右子树
- 若结点 z z z 只有一棵左子树或右子树,则让 z z z 的子树成为 z z z 父结点的子树,替代 z z z 的位置。

情况三:被删除结点有左、右两棵子树
- 若结点 z z z 有左、右两棵子树,则令 z z z 的直接后继(或直接前驱)替代 z z z,然后从二叉排序树中删去这个直接后继(或直接前驱),这样就转变成了第一或第二种情况。

二叉排序树中删除并插入某结点的分析
若在二叉排序树中删除并插入某结点,得到的二叉排序树是否和原来的相同?
不一定。这个问题需要考虑删除和插入操作对树结构的影响,以及这些操作是否能够恢复到原始的树结构。具体分析可能涉及到树的平衡性、结点的相对位置以及操作的顺序等因素。
代码实操
结构定义
- 定义二叉排序树的结点结构体
BSTNode,包含数据域data,指向左子树的指针left和指向右子树的指针right。
typedef struct BSTNode {ElemType data;struct BSTNode *left;struct BSTNode *right;
} BSTNode, *BSTRoot;
插入操作
- 在二叉排序树中插入值 x,递归地找到正确的位置插入新结点。
bool insertBST(BSTNode *&t, int x) {if (t == NULL) {t = (BSTNode*)malloc(sizeof(BSTNode));t->data = x;t->left = t->right = NULL;return true; // 插入成功}if (x == t->data)return false; // 插入失败if (x < t->data)insertBST(t->left, x);elseinsertBST(t->right, x);return true;
}
查找操作
- 在二叉排序树中查找关键字 key,递归地遍历树直到找到或到达叶子结点。
BSTNode* searchBST(BSTNode *t, int key) {if (t == NULL || t->data == key)return t;if (key < t->data)return searchBST(t->left, key);else return searchBST(t->right, key);
}
删除操作
- 删除二叉排序树中关键字为 key 的结点,处理三种情况:无子结点、一个子结点、两个子结点。
bool removeBST(BSTNode *&t, int key) {if (t == NULL)return false; // 删除失败if (key < t->data)removeBST(t->left, key);else if (key > t->data)removeBST(t->right, key);else {BSTNode *p = NULL;if (t->left != NULL && t->right != NULL) {p = t->left;while (p->right != NULL)p = p->right;t->data = p->data;removeBST(t->left, p->data);} else {BSTNode *child = (t->left != NULL) ? t->left : t->right;p = t;t = child;free(p);}}return true;
}
中序遍历
- 对二叉排序树进行中序遍历,输出有序序列。
void sortBST(BSTNode *t) {if (t != NULL) {sortBST(t->left);printf("%d ", t->data);sortBST(t->right);}
}
六、参考资料
鲍鱼科技课件
b站免费王道课后题讲解:

网课全程班:

26王道考研书
相关文章:

26考研——查找_树形查找_二叉排序树(BST)(7)
408答疑 文章目录 三、树形查找二叉排序树(BST)二叉排序树中结点值之间的关系二叉树形查找二叉排序树的查找过程示例 向二叉排序树中插入结点插入过程示例 构造二叉排序树的过程构造示例 二叉排序树中删除结点的操作情况一:被删除结点是叶结点…...

美摄科技开启智能汽车车内互动及娱乐解决方案2.0
在科技飞速发展的今天,汽车已不再仅仅是简单的代步工具,而是逐渐演变为集出行、娱乐、社交于一体的智能移动空间。美摄科技,作为前沿视觉技术与人工智能应用的领航者,凭借其卓越的技术实力和创新精神,携手汽车行业&…...

【行驶证识别】批量咕嘎OCR识别行驶证照片复印件图片里的文字信息保存表格或改名字,基于QT和腾讯云api_ocr的实现方式
项目背景 在许多业务场景中,如物流管理、车辆租赁、保险理赔等,常常需要处理大量的行驶证照片复印件。手动录入行驶证上的文字信息,像车主姓名、车辆型号、车牌号码等,不仅效率低下,还容易出现人为错误。借助 OCR(光学字符识别)技术,能够自动识别行驶证图片中的文字信…...

Vue-admin-template安装教程
#今天配置后台管理模板发现官方文档的镜像网站好像早失效了,自己稍稍总结了一下方法# 该项目环境需要node17及以下,如果npm install这一步报错可能是这个原因 git clone https://github.com/PanJiaChen/vue-admin-template.git cd vue-admin-template n…...

21.Excel自动化:如何使用 xlwings 进行编程
一 将Excel用作数据查看器 使用 xlwings 中的 view 函数。 1.导包 import datetime as dt import xlwings as xw import pandas as pd import numpy as np 2.view 函数 创建一个基于伪随机数的DataFrame,它有足够多的行,使得只有首尾几行会被显示。 df …...

LabVIEW FPGA与Windows平台数据滤波处理对比
LabVIEW在FPGA和Windows平台均可实现数据滤波处理,但两者的底层架构、资源限制、实时性及应用场景差异显著。FPGA侧重硬件级并行处理,适用于高实时性场景;Windows依赖软件算法,适合复杂数据处理与可视化。本文结合具体案例&#x…...

【NLP 48、大语言模型的神秘力量 —— ICL:in context learning】
目录 一、ICL的优势 1.传统做法 2.ICL做法 二、ICL的发展 三、ICL成因的两种看法 1.meta learning 2.Bayesian Inference 四、ICL要点 ① 语言模型的规模 ② 提示词prompt中提供的examples数量和顺序 ③ 提示词prompt的形式(format) 五、fine-tune VS I…...

vue 中渲染 markdown 格式的文本
文章目录 需求分析第一步:安装依赖第二步:创建 Markdown 渲染组件第三步,使用实例扩展功能1. 代码高亮:2. 自定义渲染规则:需求 渲染 markdown 格式的文本 分析 在Vue 3中实现Markdown渲染的常见方法。通常有两种方式:使用现有的Markdown解析库,或者自己编写解析器…...

工业4G路由器赋能智慧停车场高效管理
工业4G路由器作为智慧停车场管理系统通信核心,将停车场内的各个子系统连接起来,包括车牌识别系统、道闸控制系统、车位检测系统、收费系统以及监控系统等。通过4G网络,将这些系统采集到的数据传输到云端服务器或管理中心,实现信息…...
)
卡尔曼滤波入门(二)
核心思想 卡尔曼滤波的核心就是在不确定中寻找最优,那么怎么定义最优呢?答案是均方误差最小的,便是最优。 卡尔曼滤波本质上是一种动态系统状态估计器,它回答了这样一个问题: 如何从充满噪声的观测数据中,…...

企业如何平稳实现从Tableau到FineBI的信创迁移?
之前和大家分享了《如何将Tableau轻松迁移到Power BI》。但小编了解到,如今有些企业更愿意选择国产BI平台。为此,小编今天以Fine BI为例子,介绍如何从Tableau轻松、低成本地迁移到国产BI平台。 在信创政策全面推进的背景下,企业数…...

蓝桥与力扣刷题(蓝桥 蓝桥骑士)
题目:小明是蓝桥王国的骑士,他喜欢不断突破自我。 这天蓝桥国王给他安排了 N 个对手,他们的战力值分别为 a1,a2,...,an,且按顺序阻挡在小明的前方。对于这些对手小明可以选择挑战,也可以选择避战。 身为高傲的骑士&a…...
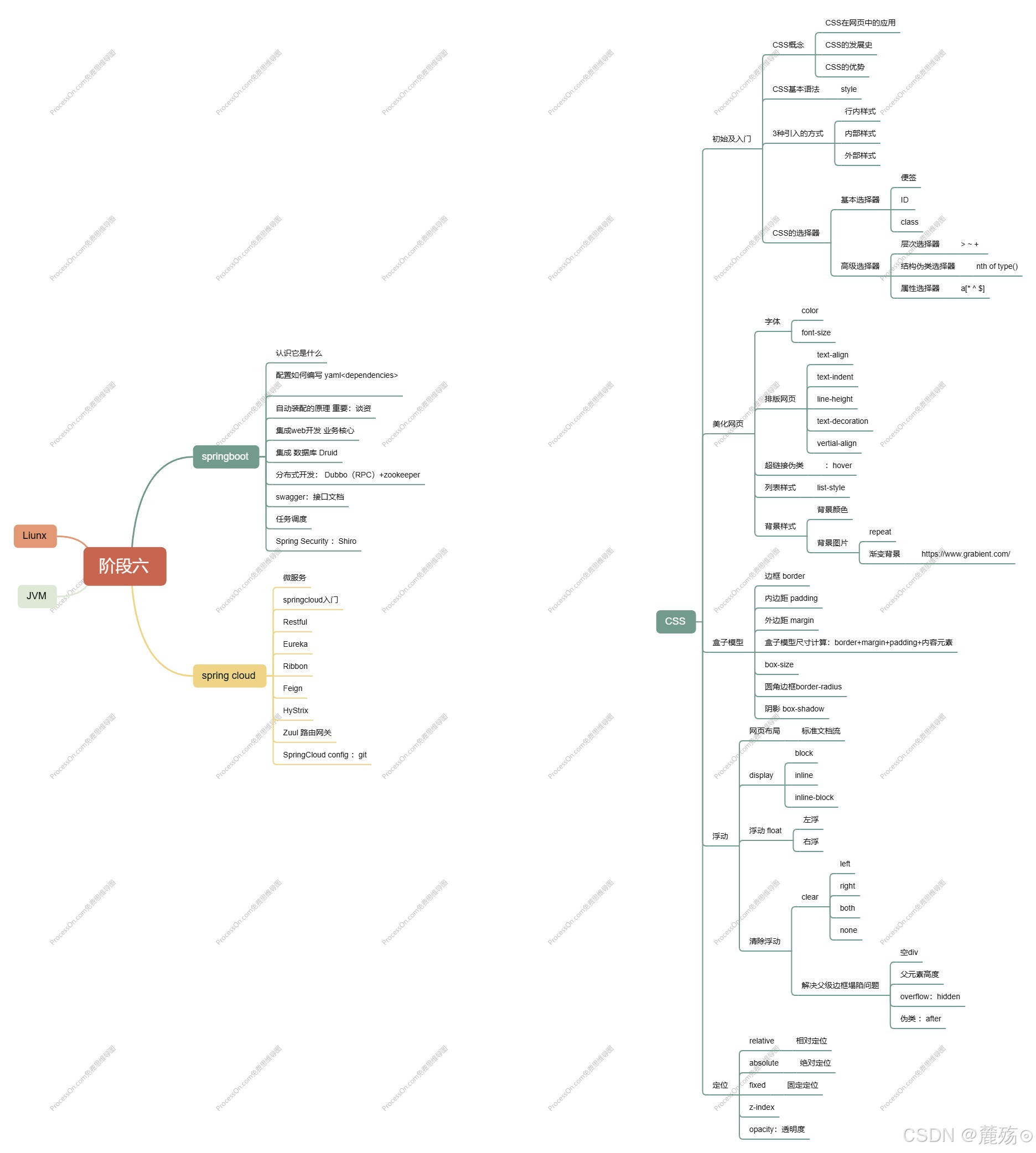
前端学习笔记--CSS
HTMLCSSJavaScript 》 结构 表现 交互 如何学习 1.CSS是什么 2.CSS怎么用? 3.CSS选择器(重点,难点) 4.美化网页(文字,阴影,超链接,列表,渐变。。。) 5…...

阶段一:Java基础语法
目标:掌握Java的基本语法,理解变量、数据类型、运算符、控制结构等。 1. Java开发环境搭建 安装JDK配置环境变量编写第一个Java程序 代码示例: // HelloWorld.java public class HelloWorld { // 定义类名为 HelloWorldpublic static vo…...

31天Python入门——第15天:日志记录
你好,我是安然无虞。 文章目录 日志记录python的日志记录模块创建日志处理程序并配置输出格式将日志内容输出到控制台将日志写入到文件 logging更简单的一种使用方式 日志记录 日志记录是一种重要的应用程序开发和维护技术, 它用于记录应用程序运行时的关键信息和…...
PyTorch张量简介)
深度学习框架PyTorch——从入门到精通(10)PyTorch张量简介
这部分是 PyTorch介绍——YouTube系列的内容,每一节都对应一个youtube视频。(可能跟之前的有一定的重复) 创建张量随机张量和种子张量形状张量数据类型 使用PyTorch张量进行数学与逻辑运算简单介绍——张量广播关于张量更多的数学操作原地修改…...

前端批量导入方式
webpack批量导入 webpack中使用 require.context 实现自动导入 const files require.context(./modules, false, /\.ts$/); const modules {}; files.keys().forEach((key) > {if (key ./index.ts) { return; }modules[key.replace(/(\.\/|\.ts)/g, )] files(key).def…...

使用ucharts写的小程序,然后让圆环中间的空白位置变大
将ringWidth属性调小 extra: { ring: { ringWidth: 20, activeOpacity: 1.5, activeRadius: 10, offsetAngle: 0, labelWidth: 15, border: true, borderWidth: 0, borderColor: #F…...

GPT-4o Image
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...

SpringMVC请求与响应深度解析:从核心原理到高级实践
一、SpringMVC架构与核心组件剖析 SpringMVC是基于Java的MVC设计模型实现的轻量级Web框架,其核心架构围绕前端控制器模式构建。以下是核心组件及其作用: DispatcherServlet 作为前端控制器,所有请求首先到达此处。它负责请求分发、协调组件协…...

大模型量化框架GPTQModel的基本使用方法
接上一篇博客:AutoGPTQ报torch._C._LinAlgError: linalg.cholesky: The factorization could not be completed的解决办法-CSDN博客 如果Llama factory量化一直报错,可以改用其他的量化框架,例如GPTQ:https://github.com/ModelCl…...

C++:函数(通识版)
一、函数的基础 1.什么是函数?(独立的功能单位) 函数是C中封装代码逻辑的基本单元,用于执行特定任务。 作用:代码复用、模块化、提高可读性。 2、函数的基本结构 返回类型 函数名(参数列表) {// 函数体return 返回值…...

Spring AI相关的面试题
以下是150道Spring AI相关的面试题目及答案: ### Spring AI基础概念类 **1. 什么是Spring AI?** Spring AI是Spring框架的扩展,旨在简化人工智能模型在Java应用中的集成与使用,提供与Spring生态无缝衔接的工具和抽象,…...

无线安灯按钮盒汽车零部件工厂的故障告警与人员调度专家
在汽车零部件制造领域,生产线故障与物料短缺等问题往往引发连锁反应,导致停机损失与成本激增。传统人工巡检与纸质工单模式已难以满足高效生产需求,而无线安灯按钮盒的智能化应用,正成为破解这一难题的关键利器。 一、精准告警&am…...

登录接口带验证码自动化(tesseract-OCR)
登录接口是很多网站和应用程序中必不可少的一部分。为了增加安全性,很多登录接口还会加入验证码的验证步骤,以防止恶意登录行为。 通常,遇到这样情况时有以下解决办法 1、使用万能验证码:如果遇到前台输入的是万能验证码…...

【Python】pillow库学习笔记2-ImageFilter类和ImageEnhance类
PIL库的ImageFilter类和ImageEnhance类提供了过滤图像和增强图像的方法。 3.ImageFilter类 ImageFilter类共提供10种预定义图像过滤方法: 方法表示描述ImageFilter.BLUR图像的模糊效果ImageFilter.CONTOUR图像的轮廓效果ImageFilter.DETAIL图像的细节效果ImageFi…...

3.Matplotlib:绘图参数文件和绘图的主要函数
一 绘图参数文件 1.绘图参数文件是什么 可以通过在程序中添加代码对参数进行配置,但是如果一个项日对于 Matplotlib 的特性参数总会设置相同的值,就没有必要在每次编写代码的时候都进行相同的配置。在代码之外使用一个永久的文件设定 Matplotlib 参数默认…...

飞书只有阅读权限的文档下载,飞书文档下载没有权限的文件
wx搜索公zhong号:"狮心王"回复"飞书文档保存"下载chrome扩展文件 拿到扩展文件之后给chrome添加扩展...
)
蓝桥杯C++基础算法-0-1背包(优化为一维)
这段代码实现了0-1 背包问题的动态规划解法,并且使用了滚动数组来优化空间复杂度。以下是代码的详细思路解析: 1. 问题背景 给定 n 个物品,每个物品有其体积 v[i] 和价值 w[i],以及一个容量为 m 的背包。目标是选择物品使得总价值…...

【开题报告+论文+源码】基于SpringBoot的智能安全与急救知识科普系统设计与实现
项目背景与意义 在全球范围内,安全与急救知识的普及已成为提升公众安全素养、减少意外伤害发生率、提高突发事件应对能力的重要举措。尤其是在当今社会,人们面临的生活、工作环境日益复杂,交通事故、火灾、溺水、突发疾病等各种意外事件的发生…...
