【day4】数据结构刷题 树
6-1 二叉树的遍历
函数接口定义:
void InorderTraversal( BinTree BT ); void PreorderTraversal( BinTree BT ); void PostorderTraversal( BinTree BT ); void LevelorderTraversal( BinTree BT );其中
BinTree结构定义如下:typedef struct TNode *Position; typedef Position BinTree; struct TNode{ElementType Data;BinTree Left;BinTree Right; };要求4个函数分别按照访问顺序打印出结点的内容,格式为一个空格跟着一个字符。
裁判测试程序样例:
#include <stdio.h> #include <stdlib.h>typedef char ElementType; typedef struct TNode *Position; typedef Position BinTree; struct TNode{ElementType Data;BinTree Left;BinTree Right; };BinTree CreatBinTree(); /* 实现细节忽略 */ void InorderTraversal( BinTree BT ); void PreorderTraversal( BinTree BT ); void PostorderTraversal( BinTree BT ); void LevelorderTraversal( BinTree BT );int main() {BinTree BT = CreatBinTree();printf("Inorder:"); InorderTraversal(BT); printf("\n");printf("Preorder:"); PreorderTraversal(BT); printf("\n");printf("Postorder:"); PostorderTraversal(BT); printf("\n");printf("Levelorder:"); LevelorderTraversal(BT); printf("\n");return 0; } /* 你的代码将被嵌在这里 */输出样例(对于图中给出的树):
Inorder: D B E F A G H C I Preorder: A B D F E C G H I Postorder: D E F B H G I C A Levelorder: A B C D F G I E H
解题思路
首先我们要知道前序遍历,中序遍历,后序遍历
前序遍历是从根节点出发,然后到左子树最后再到右子树
中序遍历是从遍历到左子树,然后再飞去根节点,最好到右子树
后序遍历是从遍历到左子树,然后再飞去右子树,最后到根节点
我们有来前序,中序和后序遍历的顺序之后,我就要开始编写代码了
层次遍历就是一层一层的从左边往右边进行遍历这棵树,这个就要用到队列的思想了
前序遍历
我们在进行前序遍历的时候,,是先遍历根然后再遍历左子树
所以我们在写递归的时候,就要先遍历根然后再遍历左子树void PreorderTraversal(BinTree BT){if(BT == NULL){return;}printf(" %c",BT -> Data);PreorderTraversal(BT -> Left);PreorderTraversal(BT -> Right); }这里我们进行根的遍历,然后再进入左子树,所以我们的printf是放在前面的
同理可得其他的情况是怎么个情况
中序遍历void InorderTraversal(BinTree BT){if(BT == NULL){return;}InorderTraversal(BT -> Left);printf(" %c",BT -> Data);InorderTraversal(BT -> Right); }后序遍历
void PostorderTraversal(BinTree BT){if(BT ==NULL){return;}PostorderTraversal(BT -> Left);PostorderTraversal(BT -> Right);printf(" %c",BT -> Data); }层次遍历
这种遍历一般是要用到队列的,但是在这个题目中,数据量没有这么大,所以博主就模拟了一个数组大小为100的队列进行操作void LevelorderTraversal(BinTree BT){BinTree array[100];int front = 0;int rear = 0;array[rear++] = BT;while(front < rear){BinTree current = array[front++];printf(" %c", current -> Data);if(current -> Left != NULL){array[rear++] = current -> Left;}if(current -> Right != NULL){array[rear++] = current -> Right;}} }这里我们可以运用这个数组再加两个变量作为队列的头指针和尾指针方便演示出队和进队的操作,然后就是我们放进来一个节点之后,就要去放入他的左孩子和右孩子,这样就可以做到层次遍历,因为是可以通过入队的顺序找到对应的孩子节点
我们数组的属性是要为树的节点的属性的,然后我们放入之后,不段的取出,然后取出之后判断这个有没有左孩子和右孩子,我们下一次取出的就是这个节点的左孩子和右孩子节点,然后按照顺序依次放入就好了
注意:我们是要从头取出,从对尾巴进入,很重要
当然博主也写出了队列的操作typedef struct Que{struct aNode* head;struct aNode* tail; }Que;typedef struct aNode{BinTree data;struct aNode* Next; }aNode;Que* creatQueue(){Que* temp = (Que*) malloc (sizeof(Que));temp -> head = NULL;temp -> tail = NULL;return temp; }void push(Que* q, BinTree root){if(q == NULL) return;aNode* temp = (aNode*) malloc (sizeof(aNode));temp -> data = root;temp -> Next = NULL;if(q -> head == NULL){q -> head = temp;q -> tail = temp;}else{q -> tail -> Next= temp;q -> tail = temp;} }BinTree pop(Que* q){if(q == NULL ||q -> head == NULL) return NULL;aNode* temp = q -> head;BinTree temp1 = temp -> data;q -> head = q -> head -> Next;if(q -> head == NULL)q -> tail = NULL;free(temp);return temp1; }void LevelorderTraversal(BinTree BT){if(BT == NULL) return;Que* q = creatQueue();push(q, BT);while(q->head != NULL){BinTree current = pop(q);printf(" %c", current -> Data);if(current -> Left != NULL){push(q, current -> Left);}if(current -> Right != NULL){push(q, current -> Right);}} }
7-1 是否同一棵二叉搜索树
给定一个插入序列就可以唯一确定一棵二叉搜索树。然而,一棵给定的二叉搜索树却可以由多种不同的插入序列得到。例如分别按照序列{2, 1, 3}和{2, 3, 1}插入初始为空的二叉搜索树,都得到一样的结果。于是对于输入的各种插入序列,你需要判断它们是否能生成一样的二叉搜索树。
输入格式:
输入包含若干组测试数据。每组数据的第1行给出两个正整数N (≤10)和L,分别是每个序列插入元素的个数和需要检查的序列个数。第2行给出N个以空格分隔的正整数,作为初始插入序列。随后L行,每行给出N个插入的元素,属于L个需要检查的序列。
简单起见,我们保证每个插入序列都是1到N的一个排列。当读到N为0时,标志输入结束,这组数据不要处理。
输出格式:
对每一组需要检查的序列,如果其生成的二叉搜索树跟对应的初始序列生成的一样,输出“Yes”,否则输出“No”。
输入样例:
4 2 3 1 4 2 3 4 1 2 3 2 4 1 2 1 2 1 1 2 0输出样例:
Yes No No
解题思路
这个题目的解题思路,我们不断地比较根节点,就是树的根节点,我们知道一棵树的有左子树和右子树,然后左子树和右子树也有对应的根节点,不断判断就好了bool dfs(int a[], int b[], int n){if(n == 0) return true;if(a[1] != b[1]) return false;int right1[20]; int left1[20]; int right2[20]; int left2[20];int r1 = 0; int l1 = 0; int r2 = 0; int l2 = 0;for(int i = 2; i<=n; i++){if(a[i] > a[1]) right1[++r1] = a[i];else left1[++l1] = a[i];if(b[i] > b[1]) right2[++r2] = b[i];else left2[++l2] = b[i];}if(r1 != r2||l1!= l2) return false;return dfs(right1, right2, r1) && dfs(left1, left2, l1); }int main(){int n, m;int num1[20]; int num2[20];while(1){scanf("%d",&n);if(n == 0) break;scanf("%d",&m);for(int i = 1; i<=n; i++){scanf("%d",&num1[i]);}for(int i = 1; i<=m; i++){bool key;for(int j = 1; j<=n; j++){scanf("%d",&num2[j]);key = dfs(num1,num2,n);}if(key== false){printf("No\n");}else{printf("Yes\n");}}} }我们再判断的时候加上四个数组和四个变量作为左子树和右子树的大小,这个比较大小的操作是可以没有的,但是为了计算量减少,我们就用了减枝
我们这个先把这个树分割为左子树和右子树,左子树和右子树的顺序很重要,我们要理解,如果子树得顺序不一样得话,那么节点得顺序就不一样
所以我们判断他们的顺序就好了,但是怎么判断顺序呢?就是不断地判断根节点就好了
7-2 堆中的路径
将一系列给定数字插入一个初始为空的最小堆 h。随后对任意给定的下标 i,打印从第 i 个结点到根结点的路径。
输入格式:
每组测试第 1 行包含 2 个正整数 n 和 m (≤103),分别是插入元素的个数、以及需要打印的路径条数。下一行给出区间 [−104,104] 内的 n 个要被插入一个初始为空的小顶堆的整数。最后一行给出 m 个下标。
输出格式:
对输入中给出的每个下标 i,在一行中输出从第 i 个结点到根结点的路径上的数据。数字间以 1 个空格分隔,行末不得有多余空格。
输入样例:
5 3 46 23 26 24 10 5 4 3输出样例:
24 23 10 46 23 10 26 10
我们要把这序列变成一个有序的一个顺序,这个也就是数组表示的一个二叉搜索树反制
#include<stdio.h> #include<string.h>long ans[10000];void adjust(int x) {while (x > 1) {int parent = x / 2;if (ans[x] < ans[parent]) {long temp = ans[x];ans[x] = ans[parent];ans[parent] = temp;x = parent;}else {break;}} }void mysort(int a[], int n, int x) {if (x == n + 1) return;ans[x] = a[x];adjust(x);mysort(a, n, x + 1); }int main() {int h, n;for (int i = 0; i < 10000; i++) {ans[i] = -10001;}scanf("%d %d", &h, &n);int num1[10000];for (int i = 1; i <= h; i++) {scanf("%d", &num1[i]);}mysort(num1, h, 1);// for (int i = 1; i <= h; i++) {// printf("%d ", ans[i]);// }for(int i = 1;i <= n; i++){int w;scanf("%d",&w);int first = 0;while(1){if(w == 0) break;if(first == 0){printf("%d",ans[w]);first = 1;}elseprintf(" %d",ans[w]);w = w/2;}printf("\n");}return 0; }解题思路
我们用递归的方法不断地排序我们的顺序,然后排序的方法我们单独写一个,递归出口就是n+1
最关键的void adjust(int x) {while (x > 1) {int parent = x / 2;if (ans[x] < ans[parent]) {long temp = ans[x];ans[x] = ans[parent];ans[parent] = temp;x = parent;}else {break;}} }这里是用到不断地对x/2来进行表示parent,然后再判断是否小于,如果小于就交换
总结
1 遍历的方法,这个后面很常用
2 判断是否是同一个二叉树,就是不断对树的根节点进行判断,而且顺序是一样的,因为插入的方法
3 堆的就是路径就是用一个while循环来往前面不断地比较
相关文章:

【day4】数据结构刷题 树
6-1 二叉树的遍历 函数接口定义: void InorderTraversal( BinTree BT ); void PreorderTraversal( BinTree BT ); void PostorderTraversal( BinTree BT ); void LevelorderTraversal( BinTree BT ); 其中BinTree结构定义如下: typedef struct TNode *Po…...

Elea AI:以人工智能之力推动病理实验室革新的技术突破与实践探索
Elea AI:以人工智能之力推动病理实验室革新的技术分析 一、病理实验室现状与 Elea AI 的革新契机 (一)传统病理实验室的痛点剖析 在医疗体系中,病理实验室扮演着至关重要的角色,其诊断结果是疾病确诊与后续治疗方案制定的关键依据。然而,当前传统病理实验室在实际运作过…...
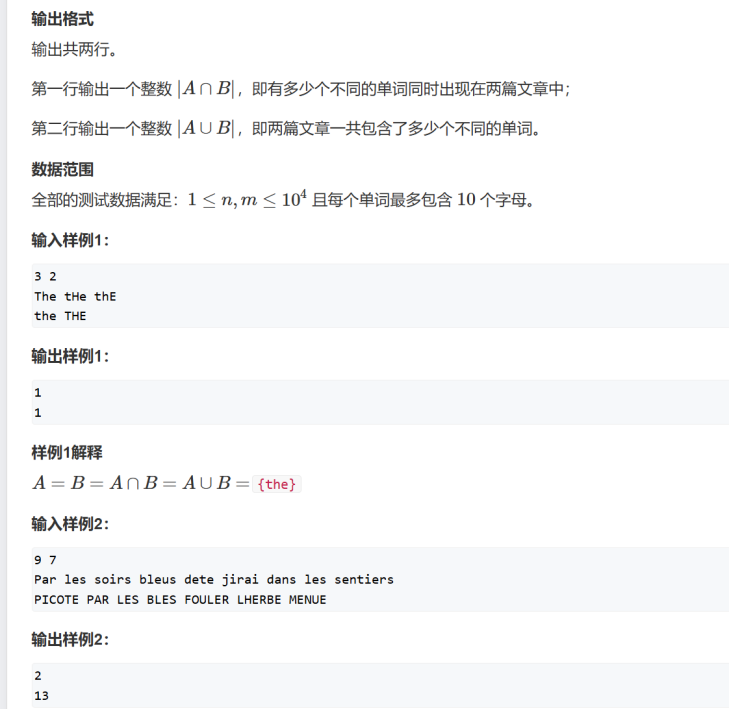
相似度计算 ccf-csp 2024-2-2
#include<bits/stdc.h> using namespace std;int main() {// 定义两个变量 n 和 m,分别用于存储两篇文章的单词个数int n, m;// 从标准输入读取 n 和 m 的值cin >> n >> m;// 定义三个 map 容器,A 用于存储并集,T 用于标记…...

多省发布!第27届中国机器人及人工智能大赛各赛区比赛通知
01 大赛介绍 中国机器人及人工智能大赛是由中国人工智能学会主办的极具影响力的全国性学科竞赛,旨在推动我国机器人及人工智能技术的创新与应用,促进相关专业的人才培养。作为全国高校学科竞赛A类赛事,该比赛吸引了众多高校和科研机构的积极…...

【Kafka】从理论到实践的深度解析
在当今数字化转型的时代,企业面临着数据量呈指数级增长、业务系统愈发复杂的挑战。在这样的背景下,高效的数据传输与处理技术成为了关键。Kafka,作为一款分布式消息队列系统,凭借其卓越的性能和丰富的特性,在众多企业的…...

对锁进行封装
目录 锁的封装 makefile编写 测试运行 RAII式封装 我们今天学习对锁进行封装。 我们在命名空间里面,在自己构建的类mutex里面完成对锁的封装。 锁的封装 我们要进行动态初始化锁,首先要有一个锁对象,所以mutex类里面的私有成员就是锁对…...
)
【学Rust写CAD】18 定点数2D仿射变换矩阵结构体(MatrixFixedPoint结构别名)
源码 // matrix/fixed.rs use crate::fixed::Fixed; use super::generic::Matrix;/// 定点数矩阵类型别名 pub type MatrixFixedPoint Matrix<Fixed, Fixed, Fixed, Fixed, Fixed, Fixed>;代码解析 这段代码定义了一个定点数矩阵的类型别名 MatrixFixedPointÿ…...

C++Primer学习(14.1 基本概念)
当运算符作用于类类型的运算对象时,可以通过运算符重载重新定义该运算符的含义。明智地使用运算符重载能令我们的程序更易于编写和阅读。举个例子,因为在Sales_item类中定义了输入、输出和加法运算符,所以可以通过下述形式输出两个Sales_item…...
)
接龙数列(最长上升 动规)
问题描述 对于一个长度为 KK 的整数数列:A1,A2,…,AKA1,A2,…,AK,我们称之为接龙数列当且仅当 AiAi 的首位数字恰好等于 Ai−1Ai−1 的末位数字 (2≤i≤K)(2≤i≤K)。例如 12,23,35,56,61,1112,23,35,56,61,11 是接龙数列;12,23,34…...

HTML跑酷
先看效果 再上代码 <!DOCTYPE html> <html> <head><title>火柴人跑酷</title><style>body {margin: 0;overflow: hidden;background: #87CEEB;}#gameCanvas {background: linear-gradient(to bottom, #87CEEB 0%, #87CEEB 50%, #228B22 …...

ChemBioServer: 一个在线“药物发现/再利用”的平台
ChemBioServer 是一个提供高级化学化合物过滤、聚类和网络分析的服务器,旨在支持药物发现和药物再利用(drug repurposing)。它集成了多种工具和网络服务,以便更高效地筛选、分析和可视化化学化合物。 网站地址: https:…...

数据结构(4)——带哨兵位循环双向链表
目录 前言 一、带哨兵的循环双向链表是什么 二、链表的实现 2.1规定结构体 2.2创建节点 2.3初始化 2.4打印 2.5检验是否为空 2.6销毁链表 2.7尾插 2.8尾删 2.9头插 2.10头删 2.11寻找特定节点 2.12任意位置插入(pos前) 2.13删除任意节点 …...

【MyBatis】MyBatis 操作数据库(入门)
文章目录 前言一、什么是MyBatis?二、MyBatis入门2.1、准备工作2.1.1 创建工程2.1.2、数据准备 2.2、配置数据库连接字符串2.3、写持久层代码2.4 单元测试 三、MyBatis的基础操作3.1 打印日志3.2、参数传递3.3、增(Insert)3.4、 删(Delete)3.5、改(Update)3.6、查(S…...

Numpy进行数组函数操作
在编程语言中,数组(Array)是最常用的数据结构之一,它可以存储一系列相同类型的元素,并且通过索引来访问或修改这些元素。在Python中,数组不仅可以通过内置的list数据类型实现,还可以借助第三方库,如NumPy来操作多维数组。掌握数组的内置函数和常用方法是成为熟练程序员…...

高速电路中的存储器应用与设计四
5 SRAM介绍及其应用要点 DRAM的性能在很大程度上受到刷新操作的影响,而SRAM则不涉及刷新,因此在相同时钟频率的条件下,SRAM的性能远高于DRAM。 SRAM的缺点是集成度低、容量小、功耗大、价格高。 在应用的场合上,SRAM毫不逊色于…...

Vue2 项目将网页内容转换为图片并保存到本地
🌟 前言 欢迎来到我的技术小宇宙!🌌 这里不仅是我记录技术点滴的后花园,也是我分享学习心得和项目经验的乐园。📚 无论你是技术小白还是资深大牛,这里总有一些内容能触动你的好奇心。🔍 &#x…...

汽车加气站操作工证书报考条件是什么?
关于汽车加气站操作工的资格证书: 一、核心证书要求 CNG充装人员上岗证 这是加气站加气工的核心资质证书,需通过专业培训并考核。该证书由相关部门颁发,证明持证人具备从事CNG(压缩天然气)充装操作的专业技能…...

动态规划--线性规划
一、https://www.lanqiao.cn/problems/3512/learning/ 解题步骤:1.dp[i]表示以i结尾最长接龙数列长度 2.每读入一个数字x...y,关注头尾的x,y来更新dp[y] 3.dp【y】 max(dp【y】,dp【x】1):如果当前数字接…...

HT81697——30W内置升压单声道D类/AB类音频功放
1 特性 ● 防削顶失真功能(防破音,Anti-Clipping Function,ACF) ● 扩频技术 ● 输出功率 28W (VBAT7.2V, RL4Ω, THDN10%, PVDD 15.5V, fiN 1kHz) 22W (VBAT7.2V,RL4Ω, THDN1%, PVDD 15.5V, fin 1kHz) 16.5W (VBAT3.7V, RL4Ω, THDN10%, PVDD 12V, fiN 1kHz) 12.8W (VBAT…...

关于ArcGIS中加载影像数据,符号系统中渲染参数的解析
今天遇到一个很有意思的问题,故记录下来,以作参考和后续的研究。欢迎随时沟通交流。如果表达错误或误导,请各位指正。 正文 当我们拿到一幅成果影像数据的时候,在不同的GIS软件中会有不同效果呈现,但这其实是影像是…...

GAMMA数据处理(十)
今天向别人请教了一个问题,刚无意中搜索到了一模一样的问题 不知道这个怎么解决... ok 解决了 有一个GAMMA的命令可转换 但是很奇怪 完全对不上 转换出来的行列号 不知道为啥 再试试 是因为经纬度坐标的小数点位数 de as...

Spring Boot属性设置方法及优先级完整说明+表格对比
Spring Boot属性设置方法及优先级完整说明 官网参考: https://docs.spring.io/spring-boot/3.4-SNAPSHOT/reference/features/external-config.html#features.external-config.files 属性设置方法优先级顺序(从高到低) 命令行参数…...

基于改进粒子群算法的多目标分布式电源选址定容规划(附带Matlab代码)
通过分析分布式电源对配电网的影响,以有功功率损耗、电压质量及分布式电源总容量为优化目标,基于模糊理论建立了分布式电源在配电网中选址定容的多目标优化模型,并提出了一种改进粒子群算法进行求解。在算例仿真中,基于IEEE-14标准…...

SAP 学习笔记 - 系统移行业务 - MALSY(由Excel 移行到SAP 的收费工具)
以前有关移行,也写过一些文章,比如 SAP 学习笔记 - 系统移行业务 - Migration cockpit工具 - 移行Material(品目)-CSDN博客 SAP 学习笔记 - 系统移行业务 - Migration cockpit工具2 - Lot导入_sap cockpit-CSDN博客 SAP学习笔记…...

2025美国网络专线国内服务商推荐
在海外业务竞争加剧的背景下,稳定高效的美国网络专线已成为外贸企业、跨国电商及跨国企业的刚需。面对复杂的国际网络环境和严苛的业务要求,国内服务商Ogcloud凭借其创新的SD-WAN技术架构与全球化网络布局,正成为企业拓展北美市场的优选合作伙…...

如何正确地在 Postman 中添加认证 Token?
在 Postman 中设置 token。我们知道 HTTP 是无状态的。token 是保持用户的登录状态或者其他数据的一种机制,从而让用户在不同页面之间保持一致的体验。 在 Postman 中添加认证 token 教程...

c++-引用
一、引用的基本概念 引用是C中一种特殊的变量别名机制,本质上是指针常量(编译器自动解引用),但语法更简洁安全。 核心特性: 必须初始化:引用在定义时必须绑定到一个已存在的对象。 类型严格匹配…...

SpringCould微服务架构之Docker(6)
容器的基本命令: 1. docker exec :进入容器执行命令 2. docker logs: -f 持续查看容器的运行日志 3. docker ps:查看所有运行的容器和状态 案例:创建运行一个容Nginx容器 docker run--name myNginx -p 80:80 -d nginx 命…...

Linux|gitlab|二进制快速安装部署gitlab-ce教程
一、 gitlab二进制文件下载地址: 官方网站: gitlab/gitlab-ce - Packages packages.gitlab.com 清华镜像站: Index of /gitlab-ce/yum/ | 清华大学开源软件镜像站 | Tsinghua Open Source Mirror gitlab分为ce也就是社区版本和ee版本,…...

java网盘项目,文件和文件夹用两个表还是一个表,两个表理论查询效率慢了为啥要用,有啥优势
java网盘项目,文件和文件夹用两个表还是一个表,两个表理论查询效率慢了为啥要用,有啥优势 根据网盘系统设计经验与数据库优化原则,独立文件夹表和文件表的设计在复杂场景下具有显著优势。以下是分表方案的核心价值与效率优化策略…...

