NO.63十六届蓝桥杯备战|基础算法-⼆分答案|木材加工|砍树|跳石头(C++)
⼆分答案可以处理⼤部分「最⼤值最⼩」以及「最⼩值最⼤」的问题。如果「解空间」在从⼩到⼤的「变化」过程中,「判断」答案的结果出现「⼆段性」,此时我们就可以「⼆分」这个「解空间」,通过「判断」,找出最优解。
这个「⼆分答案」的原理其实很容易理解,重点是如何去「判断」答案的可⾏性。
P2440 木材加工 - 洛谷
设要切成的⻓度为x ,能切成的段数为c 。根据题意,我们可以发现如下性质:
- 当x 增⼤的时候,c 在减⼩。也就是最终要切成的⻓度越⼤,能切的段数越少;
- 当x 减⼩的时候,c 在增⼤。也就是最终要切成的⻓度越⼩,能切的段数越多。
那么在整个「解空间」⾥⾯,设最终的结果是ret ,于是有: - 当x<=ret时,c>=k。也就是「要切的⻓度」⼩于等于「最优⻓度」的时候,最终切出来的段
数「⼤于等于」k ; - 当x > ret时,c < k 。也就是「要切的⻓度」⼤于「最优⻓度」的时候,最终切出来的段数
「⼩于」k;
在解空间中,根据ret的位置,可以将解集分成两部分,具有「⼆段性」,那么我们就可以「⼆分答案」。
当我们每次⼆分⼀个切成的⻓度x 的时候,如何算出能切的段数c ? - 很简单,遍历整个数组,针对每⼀根⽊头,能切成的段数就是
a[i] / x。
![![[Pasted image 20250403162611.png]]](https://i-blog.csdnimg.cn/direct/abcb1b9f15344764be1ec9fbb169cd22.png)
calc(mid) >= k -> left = mid;
calc(mid) < k -> right = mid - 1;
有-1,mid = (left + right + 1) / 2
x表示切割出来的小段的长度
c表示在x的基础下,最多能切出多少段
k表示最终要切割的段数
calc计算切割长度为x的时候,能切出来多少段
#include <bits/stdc++.h>
using namespace std;typedef long long LL;const int N = 1e5 + 10;
LL n, k;
LL a[N];LL calc(LL x)
{LL cnt = 0;for (int i = 1; i <= n; i++){cnt += a[i] / x; }return cnt;
}int main()
{ios::sync_with_stdio(false);cin.tie(0);cin >> n >> k;for (int i = 1; i <= n; i++) cin >> a[i];LL left = 0, right = 1e8;while (left < right){LL mid = (left + right + 1) / 2;if (calc(mid) >= k) left = mid;else right = mid - 1;}cout << left << endl;return 0;
}
P1873 [COCI 2011/2012 #5] EKO / 砍树 - 洛谷
设伐⽊机的⾼度为H ,能得到的⽊材为C 。根据题意,我们可以发现如下性质:
- 当H 增⼤的时候,C 在减⼩;
- 当H 减⼩的时候,C 在增⼤。
那么在整个「解空间」⾥⾯,设最终的结果是ret ,于是有: - 当H<=ret时,C>=M。也就是「伐⽊机的⾼度」⼤于等于「最优⾼度」时,能得到的⽊材
「⼩于等于」M; - 当H>ret时,C<M。也就是「伐⽊机的⾼度」⼩于「最优⾼度」时,能得到的⽊材「⼤
于」M。
在解空间中,根据ret的位置,可以将解集分成两部分,具有「⼆段性」,那么我们就可以「⼆分答案」。
当我们每次⼆分⼀个伐⽊机的⾼度H 的时候,如何算出得到的⽊材C ? - 很简单,遍历整个数组,针对每⼀根⽊头,能切成的⽊材就是
a[i] - H
![![[Pasted image 20250403165351.png]]](https://i-blog.csdnimg.cn/direct/903418fd194b449ebba770c83fb72229.png)
calc(mid) >= M -> left = mid;
calc(mid) < M -> right = mid - 1;
有-1,mid = (left + right + 1) / 2
h表示伐木机的高度
c表示在h的基础下,所能获得的木材
calc计算高度为h的时候,所能获得的木材
#include <bits/stdc++.h>
using namespace std;typedef long long LL;
const int N = 1e6 + 10;
LL n, m;
LL a[N];LL calc(LL x)
{LL ret = 0;for (int i = 1; i <= n; i++){if (a[i] > x) ret += a[i] - x; }return ret;
}int main()
{ios::sync_with_stdio(false);cin.tie(0);cin >> n >> m;for (int i = 1; i <= n; i++) cin >> a[i];LL left = 1, right = 2e9;while (left < right){LL mid = (left + right + 1) / 2;if (calc(mid) >= m) left = mid;else right = mid - 1;}cout << left << endl;return 0;
}
P2678 [NOIP 2015 提高组] 跳石头 - 洛谷
设每次跳的最短距离是x ,移⾛的⽯头块数为c 。根据题意,我们可以发现如下性质:
- 当x 增⼤的时候,c 也在增⼤;
- 当x 减⼩的时候,c 也在减⼩。
那么在整个「解空间」⾥⾯,设最终的结果是ret ,于是有: - 当x<=ret时,c<=M。也就是「每次跳的最短距离」⼩于等于「最优距离」时,移⾛的⽯头块数「⼩于等于」M;
- 当x>ret时,c>M。也就是「每次跳的最短距离」⼤于「最优距离」时,移⾛的⽯头块数「⼤于」M。
在解空间中,根据ret的位置,可以将解集分成两部分,具有「⼆段性」,那么我们就可以「⼆分答案」。
当我们每次⼆分⼀个最短距离x 时,如何算出移⾛的⽯头块数c ? - 定义前后两个指针i, j 遍历整个数组,设i ≤ j ,每次j 从i 的位置开始向后移动;
- 当第⼀次发现
a[j] - a[i] ≥ x时,说明[i + 1, j - 1]之间的⽯头都可以移⾛; - 然后将i 更新到j 的位置,继续重复上⾯两步。
![![[Pasted image 20250403193116.png]]](https://i-blog.csdnimg.cn/direct/3a2fd4cdf9ed4bfabc594eb83dad238f.png)
calc(mid) <= M -> left = mid;
calc(mid) > M -> right = mid - 1;
有-1,mid = (left + right + 1) / 2
x表示最短跳跃高度
c表示在x的基础下,移走岩石的数目
#include <bits/stdc++.h>
using namespace std;typedef long long LL;
const int N = 5e4 + 10;
LL l, n, m;
LL a[N];LL calc(LL x)
{LL ret = 0;for (int i = 0; i <= n; i++){int j = i+1;while (j <= n && a[j] - a[i] < x) j++;ret += j - i - 1;i = j-1;}return ret;
}int main()
{ios::sync_with_stdio(false);cin.tie(0);cin >> l >> n >> m;for (int i = 1; i <= n; i++) cin >> a[i];a[n + 1] = l;n++;LL left = 1, right = l;while (left < right){LL mid = (left + right + 1) / 2;if (calc(mid) <= m) left = mid;else right = mid - 1;}cout << left << endl;return 0;
}
相关文章:

NO.63十六届蓝桥杯备战|基础算法-⼆分答案|木材加工|砍树|跳石头(C++)
⼆分答案可以处理⼤部分「最⼤值最⼩」以及「最⼩值最⼤」的问题。如果「解空间」在从⼩到⼤的「变化」过程中,「判断」答案的结果出现「⼆段性」,此时我们就可以「⼆分」这个「解空间」,通过「判断」,找出最优解。 这个「⼆分答案…...

深层储层弹塑性水力裂缝扩展机理
弹性与弹塑性储层条件下裂缝形态对比 参考: The propagation mechanism of elastoplastic hydraulic fracture in deep reservoir | International Journal of Coal Science & Technology...

循环神经网络 - 机器学习任务之异步的序列到序列模式
前面我们学习了机器学习任务之同步的序列到序列模式:循环神经网络 - 机器学习任务之同步的序列到序列模式-CSDN博客 本文我们来学习循环神经网络应用中的第三种模式:异步的序列到序列模式! 一、基本概述: 异步的序列到序列模式…...

什么是检索增强生成(RAG)
1、什么是检索增强生成(RAG) 1.1 检索增强生成的概念 检索增强生成(Retrieval-Augmented Generation, RAG)是一种结合了信息检索和文本生成技术的新型自然语言处理方法。这种方法增强了模型的理解和生成能力。 相较于经典生成…...
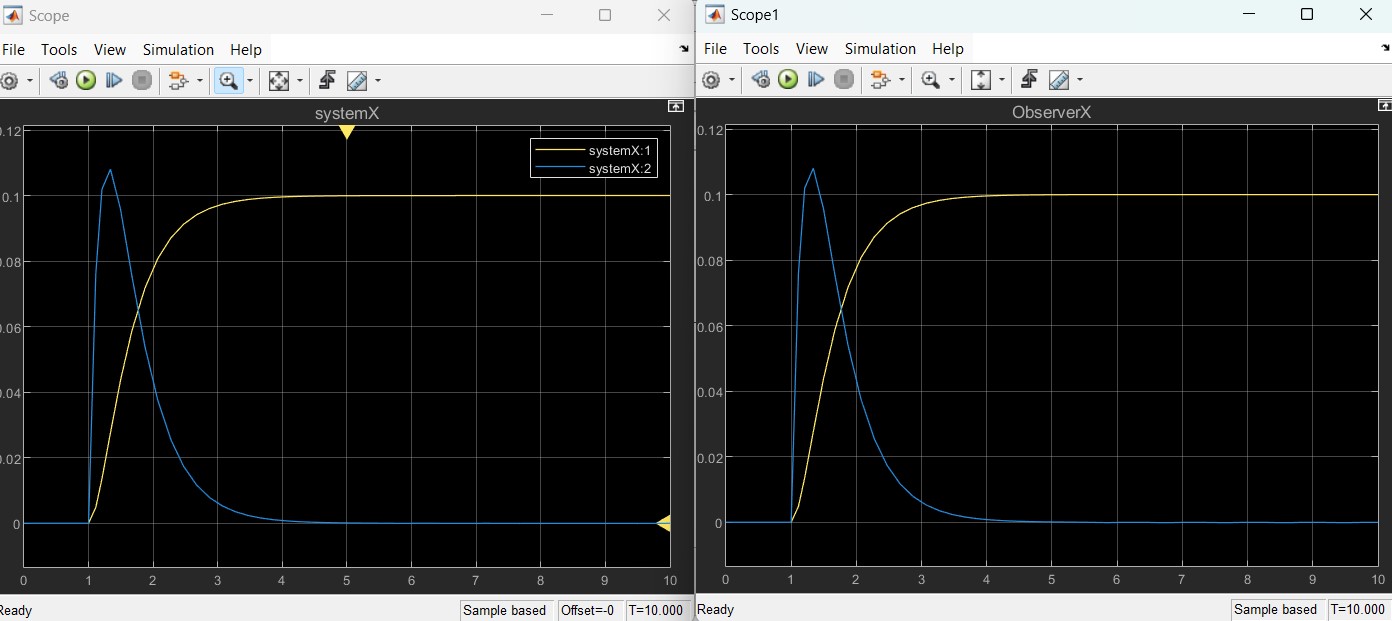
MATLAB 控制系统设计与仿真 - 33
状态反馈控制系统 -全维状态观测器的实现 状态观测器的建立解决了受控系统不能测量的状态重构问题,使得状态反馈的工程实现成为可能。 考虑到系统的状态方程表达式,如果{A,B}可控,{A,C}可观,且安装系统的性能指标,可…...

PM2 在 Node.js 项目中的使用与部署指南
一、PM2 简介 PM2 是一个带有负载均衡功能的 Node.js 应用程序的进程管理器。它可以让你的 Node.js 应用程序始终保持运行状态,即使出现错误或服务器重启也能自动恢复。同时,它还提供了诸如日志管理、性能监控等实用功能,极大地简化了 Nod…...

企业管理系统的功能架构设计与实现
一、企业管理系统的核心功能模块 企业管理系统作为现代企业的中枢神经系统,涵盖了多个核心功能模块,以确保企业运营的顺畅与高效。这些功能模块通常包括: 人力资源管理模块:负责员工信息的录入、维护、查询及统计分析,…...

RTOS基础 -- NXP M4小核的RPMsg-lite与端点机制回顾
一、RPMsg-lite与端点机制回顾 在RPMsg协议框架中: Endpoint(端点) 是一个逻辑通信端口,由本地地址(local addr)、远程地址(remote addr)和回调函数组成。每个消息都会发送到特定的…...

Cursor的主要好处
以下是Cursor的主要好处: 代码生成与优化 • 快速生成代码:根据简短描述或部分代码片段,Cursor能快速生成完整代码模块,还能智能预测下一步操作,将光标放在合适位置,让开发者一路Tab键顺滑编写代码。 • …...

覆盖学术、职场、生活的专业计算工具
软件介绍 今天要给大家介绍一款超给力的工具软件——CalcKit 计算器。它就像是你口袋里的智能计算专家,轻松化解日常生活中的各类计算难题。无论是简单的数字加减乘除,还是复杂的专业运算,它都不在话下。 这款软件内置了极为强大的计算功能…...

【大模型系列篇】大模型基建工程:基于 FastAPI 自动构建 SSE MCP 服务器 —— 进阶篇
🔥🔥🔥 上期 《大模型基建工程:基于 FastAPI 自动构建 SSE MCP 服务器》中我们使用fastapi-mcp自动挂载fastapi到mcp工具,通过源码分析和实践,我们发现每次sse请求又转到了内部fastapi RESTful api接口&…...

嵌入式硬件篇---USBUART串口
文章目录 前言一、UART 通信原理1.发送原理2.接收原理二、单片机UART接收十六进制数的处理方式1.数据解析2.数据存储3.执行相应操作三、USB通信原理四、USB 转串口通信1.硬件连接2.驱动程序3.数据传输过程五、通信特点与应用场景1.USB通信特点与应用场景2.串口通过特点与应用场…...

湖南移动广东电信DNS
湖南移动DNS: DNS 1: 111.8.14.18 DNS 2: 211.142.211.124 DNS 3: 2409:8050:2000::1 DNS 4: 2409:8050:2000:1000::1 湖南电信DNS: DNS 1: 59.51.78.210 DNS 2: 222.246.129.80 DNS 3: 240e:50:c800::210 DNS 4: 240e:50:5000::80 广东电信DNS: DNS 1…...

百度查询的ip与命令行输入 ipconfig 显示的IP地址有以下主要区别:
IP类型不同 百度中的IP是公网IP(WAN IP),由运营商分配,用于在互联网上标识你的网络出口。 ipconfig 显示的是本地IP(LAN IP),通常是路由器分配给设备的私有地址(如192.168.x.x、10.…...

【python】Plot a Square
文章目录 1、功能描述2、代码实现3、效果展示4、完整代码5、涉及到的库函数 更多有趣的代码示例,可参考【Programming】 1、功能描述 用 python 实现,以 A和B两个点为边长,方向朝 C 绘制正方形 思路: 计算向量 AB 和 AC。使用向…...

实战打靶集锦-37-Wpwnvm
文章目录 1. 主机发现2. 端口扫描&服务枚举3. 服务探查4. 系统提权 靶机地址:https://download.vulnhub.com/wpwn/wpwnvm.zip 1. 主机发现 目前只知道目标靶机在192.168.37.xx网段,通过如下的命令,看看这个网段上在线的主机。 $ nmap -…...

三、GPIO
一、GPIO简介 GPIO(General Purpose Input Output)通用输入输出口GPIO引脚电平:0V(低电平)~3.3V(高电平),部分引脚可容忍5V 容忍5V,即部分引脚输入5V的电压,…...

Guava Cache 实战:构建高并发场景下的字典数据缓存
一、场景背景 在系统开发中,字典数据(如状态类型、分类数据)具有以下特点: 高频读取(每个请求都可能涉及)低频变化(管理员修改后才会变更)数据一致性要求适中(允许分钟…...

混杂模式(Promiscuous Mode)与 Trunk 端口的区别详解
一、混杂模式(Promiscuous Mode) 1. 定义与工作原理 定义:混杂模式是网络接口的一种工作模式,允许接口接收通过其物理链路的所有数据包,而不仅是目标地址为本机的数据包。工作层级:OSI 数据链路层&#x…...

rknn_convert的使用方法
rknn_convert是RKNN-Toolkit2提供的一套常用模型转换工具,通过封装上述API接口,用户只需编辑模型对应的yml配置文件,就可以通过指令转换模型。以下是如何使用rknn_convert工具的示例命令以及支持的指令参数: python -m rknn.api.…...
)
Turtle综合案例实战(绘制复杂图形、小游戏)
在学习了 Turtle 基本的绘图技巧后,我们可以通过结合多个概念和技巧,绘制复杂的图形或实现简单的小游戏。本章将介绍两个实战案例: 绘制复杂图形:结合前面所学的知识,绘制一个精美的多层次复杂图案。简单的游戏:利用 Turtle 实现一个简单的小游戏——蛇形游戏,这是一个经…...

[dp5_多状态dp] 按摩师 | 打家劫舍 II | 删除并获得点数 | 粉刷房子
目录 1.面试题 17.16. 按摩师 题解 2.打家劫舍 II 题解 3.删除并获得点数 题解 4.粉刷房子 题解 一定要有这样的能力,碰到一个新题的时候,可以往之前做过的题方向靠! 打家劫舍问题模型: 不能选择相邻的两个数,并且要最终…...

DM数据库配置归档模式的两种方式
归档模式,联机日志文件中的内容保存到硬盘中,形成归档日志文件(REDO日志)。 采用归档模式会对系统的性能产生些许影响,然而系统在归档模式下运行会更安全,当 出现故障时其丢失数据的可能性更小,这是因为一旦出现介质故…...

Leetcode 2440 -- dfs | 枚举
题目描述 创建价值相同的连通块 思路 代码 class Solution { public:int componentValue(vector<int>& nums, vector<vector<int>>& edges) {// get max_val and sum_valint n nums.size();int max_val -1, sum_val 0;for(auto &x : nums) m…...
 和 :xx.sync 实现同步数据的做法)
Vue 中 this.$emit(“update:xx“,value) 和 :xx.sync 实现同步数据的做法
在 Vue 2.x 中,this.$emit(update:xx, value) 和 xx.sync 都是用来实现父子组件之间的数据同步的方式,它们背后的工作原理有些相似,但语法上有所不同。让我们逐个详细解释这两者的使用方式。 xx.sync(语法糖) xx.syn…...

Agent TARS与Manus的正面竞争
Agent TARS 是 Manus 的直接竞争对手,两者在 AI Agent 领域形成了显著的技术与生态对抗。 一、技术架构与功能定位的竞争 集成化架构 vs 模块化设计 Agent TARS 基于字节跳动的 UI-TARS 视觉语言模型,将视觉感知、推理、接地(grounding&#…...

【Tauri2】013——前端Window Event与创建Window
前言 【Tauri2】012——on_window_event函数-CSDN博客https://blog.csdn.net/qq_63401240/article/details/146909801?spm1001.2014.3001.5501 前面介绍了on_window_event,这个在Builder中的方法,里面有许多事件,比如Moved,Res…...
创建Linux虚拟环境并远程连接,finalshell自定义壁纸
安装VMware 这里不多赘述。 挂载Linux系统 1). 打开Vmware虚拟机,打开 编辑 -> 虚拟网络编辑器(N) 选择 NAT模式,然后选择右下角的 更改设置。 设置子网IP为 192.168.100.0,然后选择 应用 -> 确定。 解压 CentOS7-1.zip 到一个比较大…...

DBAPI设置服务器开机自启动
在 /etc/systemd/system 目录下创建一个新的服务文件,例如 dbapi.service [Unit] Descriptiondbapi standalone Service Afternetwork.target[Service] ExecStart/your-path/dbapi-enterprise-4.2.2/bin/dbapi.sh start standalone Restartalways Userroot[Install…...

基于pycharm的YOLOv11模型训练方法
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、前期准备1.1 软件环境配置1.2 训练集参考 二、训练步骤2.1 打开文件夹2.2 打开文件2.3 data.yaml最终代码 三、train.py四、最终结果五、detect.py六、 拓展…...
