【LeetCode Solutions】LeetCode 146 ~ 150 题解

LeetCode 146. LRU 缓存（中等）

【题目描述】

请你设计并实现一个满足 LRU（最近最少使用）缓存约束的数据结构。

实现 LRUCache 类：

• LRUCache(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存；
• int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1。
• void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value；如果不存在，则向缓存中插入该组 key-value。如果插入操作导致关键字数量超过 capacity，则应该逐出最久未使用的关键字。

函数 get 和 put 必须以 $O(1)$ 的平均时间复杂度运行。

【示例 1】

输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1);    // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2);    // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1);    // 返回 -1 (未找到)
lRUCache.get(3);    // 返回 3
lRUCache.get(4);    // 返回 4

【提示】

$1<=capacity<=3000$
$0<=key<=10000$
$0<=value<=10^5$
最多调用 $2\ast 10^5$ 次 get 和 put

---

【分析】

使用哈希表可以实现时间复杂度为 $O(1)$ 的增删改查，但是还需要实现 LRU 的机制，我们要能够修改每个键值对的时间戳，同时还能够快速找到时间戳最小的键值对。

可以用一个双链表维护这个时间戳，时间戳最新的节点在头部，最旧的节点在尾部，哈希表用于从 key 映射到对应的节点，这样查找双链表的节点就是 $O(1)$ 的，从而双链表的插入与删除操作也是 $O(1)$ 的。

---

【代码】

class LRUCache {
private:struct Node {int key, val;Node *left, *right;Node(int key, int val): key(key), val(val), left(nullptr), right(nullptr) {}}*L, *R;int n;unordered_map<int, Node*> hash;void insert(Node* p) {  // 将 p 插入到链表的首部p->left = L, p->right = L->right;L->right->left = p, L->right = p;}void remove(Node* p) {  // 将 p 从链表中删除p->left->right = p->right;p->right->left = p->left;}public:LRUCache(int capacity) {n = capacity;L = new Node(-1, -1), R = new Node(-1, -1);L->right = R, R->left = L;}int get(int key) {if (!hash.count(key)) return -1;Node* p = hash[key];remove(p);insert(p);return p->val;}void put(int key, int value) {if (!hash.count(key)) {if (hash.size() == n)  // 容量满了则删除链表的最后一个点hash.erase(R->left->key), remove(R->left);hash[key] = new Node(key, value);insert(hash[key]);} else {Node* p = hash[key];p->val = value;remove(p);insert(p);}}
};/*** Your LRUCache object will be instantiated and called as such:* LRUCache* obj = new LRUCache(capacity);* int param_1 = obj->get(key);* obj->put(key,value);*/

LeetCode 147. 对链表进行插入排序（中等）

【题目描述】

给定单个链表的头 head，使用插入排序对链表进行排序，并返回排序后链表的头。

插入排序算法的步骤：

1. 插入排序是迭代的，每次只移动一个元素，直到所有元素可以形成一个有序的输出列表。
2. 每次迭代中，插入排序只从输入数据中移除一个待排序的元素，找到它在序列中适当的位置，并将其插入。
3. 重复直到所有输入数据插入完为止。

下面是插入排序算法的一个图形示例。部分排序的列表（黑色）最初只包含列表中的第一个元素。每次迭代时，从输入数据中删除一个元素（红色），并就地插入已排序的列表中。

对链表进行插入排序。

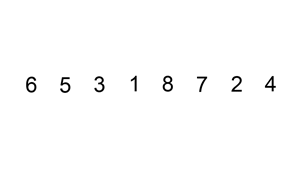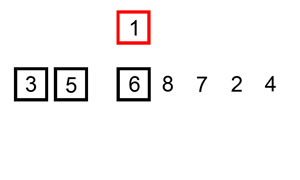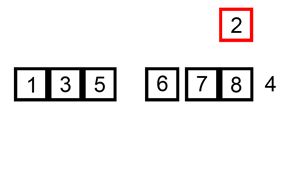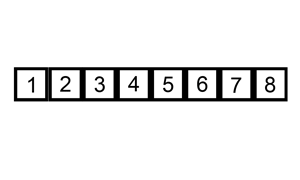
【示例 1】

输入: head = [4,2,1,3]
输出: [1,2,3,4]

【示例 2】

输入: head = [-1,5,3,4,0]
输出: [-1,0,3,4,5]

【提示】

列表中的节点数在 $[1,5000]$ 范围内
$-5000<=Node.val<=5000$

---

【分析】

对于当前要插入的点，我们要在已排序区间中找到第一个大于当前点的位置，将当前点插入到这个更大的点的前面。如果当前点前面的点都小于等于自身，则直接插入在区间末尾即可。

---

【代码】

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* insertionSortList(ListNode* head) {ListNode* dummy = new ListNode(-1, head);ListNode* p = head->next;head->next = nullptr;  // 刚开始已排序区间只有头节点，先将其 next 置为空标记排序区间的末尾while (p) {ListNode* cur = dummy;while (cur->next && cur->next->val <= p->val) cur = cur->next;ListNode* q = p->next;if (!cur->next)  // p 比已排序节点都更大则接在已排序区间的末尾p->next = nullptr, cur->next = p;else  // 否则 cur->next 是第一个大于 p 的节点，将 p 插入到 cur 后面p->next = cur->next, cur->next = p;p = q;}return dummy->next;}
};

LeetCode 148. 排序链表（中等）

【题目描述】

给你链表的头结点 head，请将其按升序排列并返回排序后的链表。

【示例 1】

输入：head = [4,2,1,3]
输出：[1,2,3,4]

【示例 2】

输入：head = [-1,5,3,4,0]
输出：[-1,0,3,4,5]

【示例 3】

输入：head = []
输出：[]

【提示】

链表中节点的数目在范围 $[0,5\ast 10^4]$ 内
$-10^5<=Node.val<=10^5$

进阶：你可以在 $O(nlogn)$ 时间复杂度和常数级空间复杂度下，对链表进行排序吗？

---

【分析】

由于快排和递归的归并排序都需要递归，空间复杂度为 $O(logn)$，只有迭代的归并排序可以实现 $O(1)$ 的空间复杂度。

用迭代实现归并排序其实就是自底向上做，即刚开始的时候每个节点自身就是一个独立的区间。

第一次迭代的时候将每个长度为 1 的区间两两进行合并，成为一个长度为 2 的有序区间，然后下一轮就将每个长度为 2 的区间合并成长度为 4 的区间，以此类推。

本题的代码实现比较复杂，不太理解可以画个图模拟一下。

---

【代码】

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* sortList(ListNode* head) {int n = 0;  // 链表长度for (ListNode* p = head; p; p = p->next) n++;for (int i = 1; i < n; i *= 2) {  // 枚举要合并的每一段长度ListNode *dummy = new ListNode(-1),*cur = dummy;  // dummy->next 是合并后上一层的头节点for (int j = 0; j < n; j += i * 2) {  // 需要合并的次数为 (n + 1) / i * 2ListNode *p = head, *q = head;for (int k = 0; k < i && q; k++) q = q->next;  // q 向后跳 i 次到另一段的头部int l = 0, r = 0;  // 左右两段已合并的节点数while (l < i && r < i && p && q) {  // 只要两段都不为空且还有节点没合并则进行对比合并if (p->val <= q->val) cur = cur->next = p, p = p->next, l++;else cur = cur->next = q, q = q->next, r++;}while (l < i && p) cur = cur->next = p, p = p->next, l++;  // 合并左段剩余的节点while (r < i && q) cur = cur->next = q, q = q->next, r++;  // 合并右段剩余的节点if (q) head = q;  // head 移动到后面两段区间的头部}cur->next = nullptr;  // 合并完成后将末尾节点的 next 置为空head = dummy->next;}return head;}
};

LeetCode 149. 直线上最多的点数（困难）

【题目描述】

给你一个数组 $points$，其中 $points[i]=[x_i,y_i]$ 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。

【示例 1】

输入：points = [[1,1],[2,2],[3,3]]
输出：3

【示例 2】

输入：points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
输出：4

【提示】

$1<=points.length<=300$
$points[i].length==2$
$-10^4<=x_i,y_i<=10^4$
points 中的所有点互不相同

---

【分析】

任意两点确定一条直线，我们可以先枚举每条直线，如果暴力枚举时间是 $O(n^2)$，然后再判断有多少个点在这条直线上，时间为 $O(n)$，因此总共的时间复杂度为 $O(n^3)$。

也可以枚举每个点，然后判断其他点到这个点的斜率是多少，也就是确定其他点与这个点所形成的直线，然后判断哪条直线上的点最多。由于垂直线没有斜率，因此可以用一个变量单独记一下。本题保证每个点不同，如果可能存在重复点那么还需要开个变量记录下相同点的数量，无论是哪条直线都要算上当前枚举点的重复点数量。

---

【代码】

class Solution {
public:int maxPoints(vector<vector<int>>& points) {int res = 0;for (auto a: points) {unordered_map<long double, int> cnt;  // long double 防止精度被卡int vc = 0;  // 与 a 在一条垂线上的点数for (auto b: points) {if (b == a) continue;if (b[0] == a[0]) vc++;else {long double k = (long double) (b[1] - a[1]) / (b[0] - a[0]);  // 记得要强制转换cnt[k]++;}}for (const auto &[k, v]: cnt) res = max(res, v + 1);res = max(res, vc + 1);}return res;}
};

LeetCode 150. 逆波兰表达式求值（中等）

【题目描述】

给你一个字符串数组 tokens，表示一个根据逆波兰表示法表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

注意：

• 有效的算符为 '+'、'-'、'*' 和 '/'。
• 每个操作数（运算对象）都可以是一个整数或者另一个表达式。
• 两个整数之间的除法总是 向零截断 。
• 表达式中不含除零运算。
• 输入是一个根据逆波兰表示法表示的算术表达式。
• 答案及所有中间计算结果可以用 32 位 整数表示。

【示例 1】

输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

【示例 2】

输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

【示例 3】

输入：tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出：22
解释：该算式转化为常见的中缀算术表达式为：((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

【提示】

$1<=tokens.length<=10^4$
tokens[i] 是一个算符（"+"、"-"、"*" 或 "/"），或是在范围 $[-200,200]$ 内的一个整数

逆波兰表达式：

逆波兰表达式是一种后缀表达式，所谓后缀就是指算符写在后面。

• 平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 )。
• 该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * )。

逆波兰表达式主要有以下两个优点：

• 去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
• 适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中。

---

【分析】

很经典的逆波兰表达式求值，提示中已经说明了做法，就是遇到数字就直接入栈，遇到运算符就出栈两个元素进行运算后将结果入栈，只要注意后出栈的那个才是被运算数，例如按顺序出栈 $x$ 和 $y$，当前操作符为 /，那么运算结果为 $y/x$。

---

【代码】

class Solution {
public:int evalRPN(vector<string>& tokens) {stack<int> stk;for (string s: tokens) {if (s != "+" && s != "-" && s != "*" && s != "/") stk.push(stoi(s));else {int x = stk.top(); stk.pop();int y = stk.top(); stk.pop();if (s == "+") stk.push(y + x);else if (s == "-") stk.push(y - x);else if (s == "*") stk.push(y * x);else stk.push(y / x);}}return stk.top();}
};