【GeoDa使用】空间自相关分析操作

使用 GeoDa 软件进行空间自相关分析

---

双击打开 GeoDa 软件

选择 .shp 文件

导入文件

 空间权重矩阵（*.gal / *.gwt）是进行任何空间分析的前提

构建空间权重矩阵

空间权重矩阵（Spatial Weights Matrix） 是一个用来描述空间对象之间相互关系的矩阵。

它反映了地理单位之间“邻接”或“距离接近”关系，是进行空间计量分析的基础。

空间权重矩阵是一个用来表示地理单元之间“谁和谁是邻居”的表格，它决定了你在进行空间分析时，哪些单元会被当作“周围环境”来计算

定义空间邻居关系

点---基于距离

Arc Distance基于球面经纬度，考虑地球曲率

	中文名称	说明	使用场景
Euclidean Distance	欧氏距离	最常见的直线距离计算方法，即“勾股定理”形式，单位与坐标系统一致。 例如： √[(x₂ - x₁)² + (y₂ - y₁)²]	坐标为投影坐标（如米、千米），一般城市区域或栅格数据分析
Arc Distance (mi)	弧线距离（英里）	基于地球球面模型计算两地之间的球面弧线距离，单位为英里	全球或跨区域分析，使用经纬度坐标数据
Arc Distance (km)	弧线距离（千米）	同上，单位为千米	全球范围分析，常用于交通、气候空间数据分析

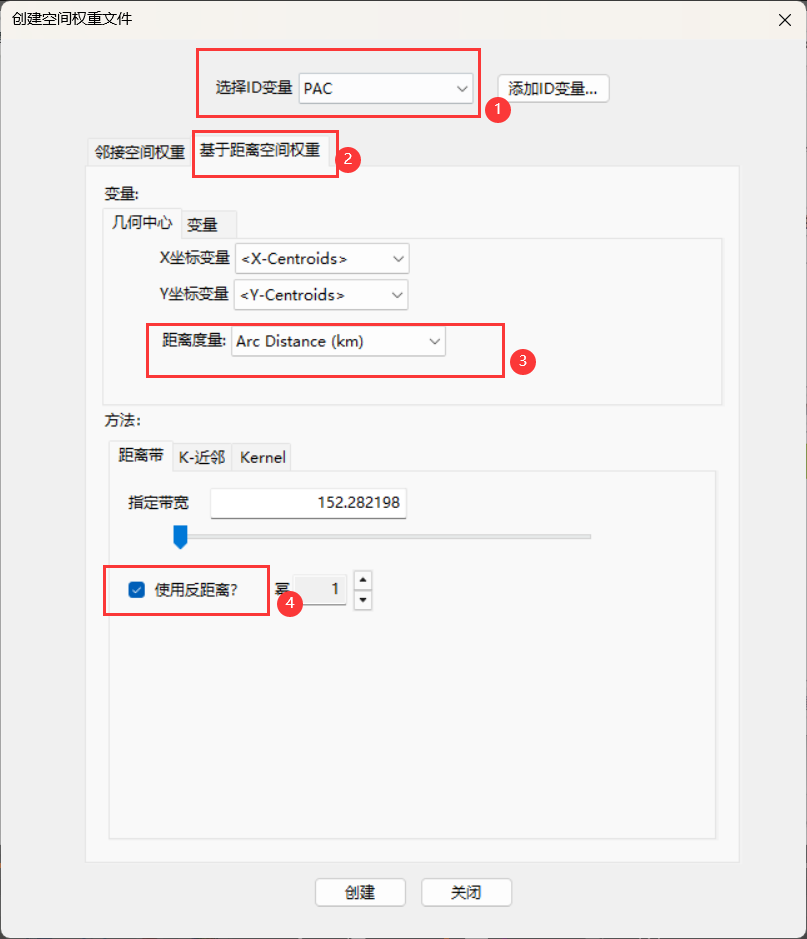
点击创建,选择保存的文件位置

创建成功后就可以关闭了

---

全局空间自相关

在菜单栏点击：

 

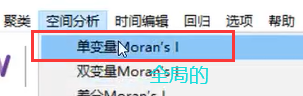
选择你想分析的变量（如：CI）

勾选使用的权重矩阵（默认的话会自动使用）

点击 ，软件会生成：

Moran’s I 值

Z-score 和 p 值（显著性）

散点图（Moran Scatter Plot）

📌 结果解读：

Moran’s I > 0：正自相关（聚集）

Moran’s I < 0：负自相关（离散）

Z 值越大，p 值越小 → 空间聚集越显著

局部空间自相关

菜单栏点击：

同样选择你分析的变量

使用默认的空间权重矩阵

点击 输出内容：

红色：High-High 聚集（热点）

蓝色：Low-Low 聚集（冷点）

粉红：High-Low（高值被低值包围）

浅蓝：Low-High（低值被高值包围）

灰色：不显著区域（p > 0.05）

选中高亮的数量

shift和鼠标配合

右下角可以看到选中数量

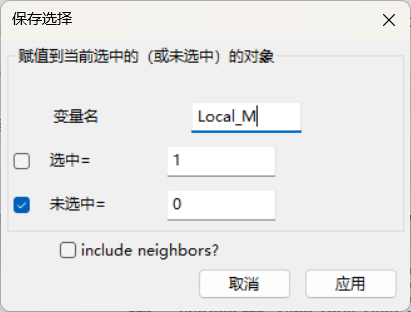
上面4步还要重做一下

点击保存,设置好后 

---

空间权重矩阵（Spatial Weight Matrix）是空间计量分析和空间数据建模中的核心工具，用来描述一个空间单元（比如一个区域、城市、网格等）与其他空间单元之间的“相邻”或“关联”关系

空间权重矩阵是一个 n × n 的矩阵，n 表示空间单元的数量，矩阵中的每一个元素 wij表示第 i 个单元与第 j 个单元之间的空间关系强度。

• 如果 wij=1，表示 i 与 jj是邻居；

• 如果 wij=0，表示两者不是邻居；

• 更复杂的形式中，wij可以是两个单元之间的距离的函数，比如反比距离 wij=1/dij

常见构建方法

邻接矩阵（Binary contiguity matrix）

• 仅表示是否相邻，常见的有：

  • Rook 邻接：四邻域（上下左右相邻才算邻居）；

  • Queen 邻接：八邻域（包括对角线）

距离衰减矩阵（Distance-based weight）

根据单元之间的实际距离构建，距离越远，权重越小

一般 α=1 或 2；d是距离

距离阈值：超出距离就设为 0

准化权重矩阵

对每一行做归一化，

可以防止单位之间邻居数量不一致带来的影响