图论:最小生成树
最小生成树 (无向无环图)
概念

1.Prim算法 P3366 【模板】最小生成树 - 洛谷

邻接矩阵实现
#include<iostream>
#include<cstring>
using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 5e3 + 10;
int dis[N]; //记录每个结点到其他结点的巨鹿
bool st[N];//记录每个节点是否被遍历过int edge[N][N];//记录每个结点到其他结点的巨鹿int n, m;//prim算法实现
int prim()
{//把dis初始化成无穷大memset(dis, INF, sizeof(dis));dis[1] = 0;//第一个结点开头int ret = 0;for (int i = 1; i <= n; i++){int t = 0;//找最近点for (int j = 1; j <= n; j++){if (!st[j] && dis[j] < dis[t])t = j;//更新最小值的下标}//判断是否联通if (dis[t] == INF)return INF;//把该点加进去st[t] = true;ret += dis[t];//更新disfor (int i = 1; i <= n; i++){if (dis[i] > edge[t][i])//如果距离大于新的结点距离其他节点的距离,更新dis[i] = edge[t][i];}}return ret;
}int main()
{cin >> n >> m;memset(edge, INF, sizeof(edge));for (int i = 1; i <= m; i++){int x, y, z; cin >> x >> y >> z;//注意有重边的情况,注意是取笑,初始化为无穷大edge[x][y] = edge[y][x] = min(edge[x][y], z);}int ret = prim();if (ret == INF)cout << "orz" << endl;elsecout << ret << endl;
}vector数组实现
#include<iostream>
#include<cstring>
#include<vector>
using namespace std;typedef pair<int, int> PII;//连接的点,权值
const int INF = 0x3f3f3f3f;
const int N = 5e3 + 10;int n, m;
int dis[N];
bool st[N];
vector<PII> dp[N];int prim()
{memset(dis, INF, sizeof(dis));dis[1] = 0;int ret = 0;for (int i = 1; i <= n; i++)//加入n个点,功德圆满{//找最近的点int t = 0;//dis[0]给初始化成INF了for (int j = 1; j<= n; j++){if (!st[j] && dis[j] < dis[t])//没有被访问过并且比t小,更新t{t = j;}}//判断是否联通if (dis[t] == INF)return INF;st[t] = true;ret += dis[t];//更新disfor (auto& x : dp[t]){int a = x.first;//相连的点int b = x.second;//相连的点的权值/*if (dis[a] > b)dis[a] = b;*/dis[a] = min(dis[a], b);//这里可以解决重边的情况}}return ret;
}int main()
{cin >> n >> m;for (int i = 1; i <= m; i++){int x, y, z; cin >> x >> y >> z;dp[x].push_back({ y,z });dp[y].push_back({ x,z });}int ret = prim();if (ret == INF)cout << "orz" << endl;elsecout << ret << endl;
}2.克鲁斯卡尔算法(并查集实现)


P3366 【模板】最小生成树 - 洛谷
#include<iostream>
#include<algorithm>
using namespace std;const int N = 5010;//点
const int M = 2e5 + 10;//边
const int INF = 0x3f3f3f3f;struct node
{int x, y, z;
}a[M];int f[N];//并查集
int n, m;int find(int x)
{return f[x] == x ? x : f[x] = find(f[x]);
}
void un(int x, int y)
{f[find(x)] = find(y);
}bool cmp(node& x, node& y)
{return x.z < y.z;
}int kruskal()
{int ret = 0;int cnt = 0;for (int i = 1; i <= m; i++){int x = a[i].x, y = a[i].y, z = a[i].z;if (find(x) != find(y))//没有并在一起,就整{cnt++;//记录边的个数,最小生成树,节点数n,边数n-1ret += z;un(x, y);}}if (cnt != n-1)return INF;//成功的话是n - 1,没有说明不联通return ret;
}int main()
{cin >> n >> m;for (int i = 1; i <= m; i++){cin >> a[i].x >> a[i].y >> a[i].z;}//并查集初始化for (int i = 1; i <= n; i++)f[i] = i;//排序,从小到大sort(a + 1, a + 1 + m, cmp);int ret = kruskal();if (ret == INF)cout << "orz" << endl;elsecout << ret << endl;
}
P1194 买礼物 - 洛谷


#include<iostream>
#include<algorithm>
using namespace std;const int N = 500*500+10;//结点*结点 == 边的个数,我们存的是边的个数
const int M = 1010;
int a, n;//A和节点数
int pos;//有几条边要存
int f[N];//并查集struct node
{int x, y, z;
}b[N];//存边之间的个数bool cmp(node& x, node& y)//排序
{return x.z < y.z;
}int find(int x)
{return f[x] == x ? x : f[x] = find(f[x]);
}
//克鲁斯卡尔算法
int kk()
{int ret = 0;//总价int cnt = 0;//几条边,用来计算分成几块,有几块就*多少个Afor (int i = 1; i <= pos; i++){int x = b[i].x, y = b[i].y, z = b[i].z;//取出边的数据int fx = find(x);int fy = find(y);if (fx != fy && z < a && z != 0){ret += z;cnt++;//计算有多少条边f[find(x)] = find(y);//合并}}ret += (n - cnt) * a;//有几块树return ret;
}int main()
{cin >> a >> n;for (int i = 1; i <= n; i++){for (int j = 1; j <= n; j++){int k; cin >> k;//只需要存一条边的关系//但其实就算不要也无所谓,因为并查集合并后,也不会要重复的//克鲁斯卡尔算法只需要存取,边的数据就好了,不重复更好if (i >= j)continue;pos++;b[pos].x = i, b[pos].y = j, b[pos].z = k;}}for (int i = 1; i <= n; i++)f[i] = i;sort(b + 1, b + 1 + pos,cmp);int ret = kk();cout << ret << endl;
}P2330 [SCOI2005] 繁忙的都市 - 洛谷

瓶颈树:生成所有生成树中,最大边权值最小的那棵树。
也就是最小生成树。
最小生成树的最大边值也就是最终结果
#include<iostream>
#include<algorithm>
using namespace std;const int N = 310;
const int M = 8010;
int n, m;
int pos;
int f[N];struct node
{int x, y, z;
}a[M];int find(int x)
{return f[x] == x ? x : f[x] = find(f[x]);
}bool cmp(node& x, node& y)
{return x.z < y.z;
}int ret = 0;
void kk()
{for (int i = 1; i <= m; i++){int x = a[i].x, y = a[i].y, z = a[i].z;int fx = find(x), fy = find(y);if (fx != fy){ret = max(ret, z);f[fx] = fy;}}
}int main()
{cin >> n >> m;for (int i = 1; i <= m; i++){int x, y, z;cin >> x >> y >> z;a[i].x = x, a[i].y = y, a[i].z = z;}cout << n - 1 << " ";for (int i = 1; i <= n; i++)f[i] = i;sort(a + 1, a + 1 + m, cmp);kk();cout << ret << endl;
}P2573 [SCOI2012] 滑雪 - 洛谷


#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;typedef long long LL;const int N = 1e5 + 10;
const int M = 2e6 + 10;//考虑两重变typedef pair<int, int> PII;//可以到的点,到该点的距离int n, m;//n个景点,m条边
int h[N];//每个景点的高度vector<PII> dp[N];//记录该点可以去的所有的点+到的距离bool st[N];
LL cnt;//记录有多少个景点被访问了
int pos;//记录有多少条边struct node
{int x, y, z;
}a[M];//记录边的数据int f[N];//并查集void dfs(int u)//找所有可以到达的边
{cnt++;st[u] = true;for (auto& s : dp[u])//遍历该点可以到达的每一条边,并且进行记录{int x = s.first, y = s.second;++pos;//多一条边a[pos].x = u, a[pos].y = x, a[pos].z = y;if (!st[x])//没有被访问过{dfs(x);}}
}
bool cmp(node& x, node& y)//从该点到宁一个点的高的优先,其次是距离
{int x1 = x.x, y1 = x.y, z1 = x.z;int x2 = y.x, y2 = y.y, z2 = y.z;if (h[y1] != h[y2])return h[y1] > h[y2];return z1 < z2;
}int find(int x)
{return f[x] == x ? x : f[x] = find(f[x]);
}LL ret;
void kk()
{sort(a + 1, a + 1 + pos, cmp);for (int i = 1; i <= n; i++)f[i] = i;for (int i = 1; i <= pos; i++){int x = a[i].x, y = a[i].y, z = a[i].z;int fx = find(x);int fy = find(y);if (fx != fy){ret += z;f[fx] = fy;}}}int main()
{cin >> n >> m;for (int i = 1; i <= n; i++)cin >> h[i];for (int i = 1; i <= m; i++){int x, y, z; cin >> x >> y >> z;if (h[x] >= h[y])dp[x].push_back({ y,z });if (h[y] >= h[x])dp[y].push_back({ x,z });//如果是 == 的话,那么两边的都要记录}dfs(1);kk();cout << cnt << " "<<ret << endl;
}有向图:
由于克鲁斯卡尔算法要把所有的边进行排序没所以我们要创建一个起点,终点,边的结构体
题目没有明确给出那就自己创建。
dfs:把所有的路径都找到。(遍历到一条边就加入路径)
用胶囊把所有可以到的点统计到。->生成最小生成树。最小生成树:利用dfs找到的路径据生成最小生成树
距离最短->所有距离的总和。--->最小生成树。选边的时候,优先去往高的位置的边,其次才是距离
相关文章:

图论:最小生成树
最小生成树 (无向无环图) 概念 1.Prim算法 P3366 【模板】最小生成树 - 洛谷 邻接矩阵实现 #include<iostream> #include<cstring> using namespace std; const int INF 0x3f3f3f3f; const int N 5e3 10; int dis[N]; //记录每个结点到…...

智能多媒体处理流水线——基于虎跃办公API的自动化解决方案
在内容爆炸的时代,多媒体文件处理(图片压缩、视频转码、音频降噪)已成为内容生产者的日常挑战。本文将演示如何基于虎跃办公的多媒体处理API,构建自动化处理流水线,实现: 批量文件智能分类格式自动转换质量…...

虚拟表、TDgpt、JDBC 异步写入…TDengine 3.3.6.0 版本 8 大升级亮点
近日,TDengine 3.3.6.0 版本正式发布。除了此前已亮相的时序数据分析 AI 智能体 TDgpt,本次更新还带来了多个针对性能与易用性的重要增强:虚拟表全面上线,支持更灵活的一设备一表建模;JDBC 写入机制全新升级࿰…...

virt-manager配置NAT
在 virt-manager 中配置 NAT 模式,可以通过以下步骤完成。NAT(Network Address Translation)模式允许虚拟机通过宿主机的网络连接访问外部网络,同时对外隐藏虚拟机的真实 IP 地址。以下是具体操作步骤: 步骤 1&a…...
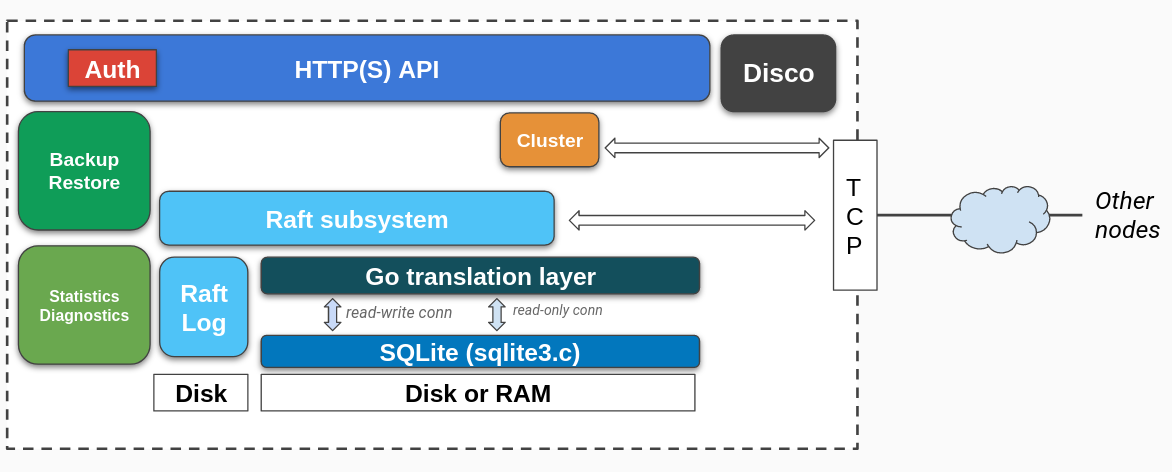
rqlite:一个基于SQLite构建的分布式数据库
今天给大家介绍一个基于 SQLite 构建的轻量级分布式关系型数据库:rqlite。 rqlite 基于 Raft 协议,结合了 SQLite 的简洁性以及高可用分布式系统的稳健性,对开发者友好,操作极其简便,其核心设计理念是以最低的复杂度实…...

Dynamics 365 Business Central Recurring Sales Lines 经常购买销售行 来作 订阅
#D365 BC ERP# #Navision# 前面有节文章专门介绍了BC 2024 Wave 2 支持的更好的Substription & Recurring Billing。 其实在D365 BC ERP中一直有一个比较简单的订阅模块Recrring Sales Lines。本文将介绍一下如何用Recurring Sales Lines来 实施简易的订阅Substription。具…...

【WebRTC】开源项目Webrtc-streamer介绍
WebRTC-Streamer 这是一个用于通过简单的信令机制(参见 api)流式传输 WebRTC 媒体源的实验项目,支持以下媒体源: 捕获设备 屏幕捕获 mkv 文件 RMTP/RTSP 源 同时该项目也兼容 WHEP 接口。 注意 * 在线演示已停止,…...

探索生成式AI在游戏开发中的应用——3D角色生成式 AI 实现
概述 自从开创性论文 Denoising Diffusion Probabilistic Models 发布以来,此类图像生成器一直在改进,生成的图像质量在多个指标上都击败了 GAN,并且与真实图像无法区分。 NeRF: Representing Scenes as Neural Radiance Fields for View S…...

androd的XML页面 跳转 Compose Activity 卡顿问题
解决 XML 点击跳转到 Compose Activity 卡顿问题 当从 XML 布局的 Activity 跳转到 Compose Activity 时出现卡顿现象,这通常是由以下几个原因导致的: 可能的原因及解决方案 1. Compose 首次初始化开销 问题:Compose 框架首次初始化需要时…...

神经网络能不能完全拟合y=x² ???
先说结论:关键看激活函数的选择 ReLU神经网络对非线性函数的拟合分析 ReLU神经网络对非线性函数(如 y x 2 y x^2 yx2)的拟合只能是逼近,而无法实现数学意义上的完全重合。这一结论源于ReLU的分段线性本质与目标函数的非线性结…...
与非逻辑视图(JSON、Excel、PDF、XML)详解及示例)
Spring MVC 逻辑视图(JSP、Thymeleaf、FreeMarker)与非逻辑视图(JSON、Excel、PDF、XML)详解及示例
Spring MVC 逻辑视图与非逻辑视图详解及示例 一、逻辑视图与非逻辑视图的定义 类型定义逻辑视图通过视图解析器(ViewResolver)将逻辑名称(如 success)映射到具体视图实现。非逻辑视图直接返回具体视图对象(如 JsonVie…...

K8s 老鸟的配置管理避雷手册
Yining, China 引言 对于这种案例,你们的处理思路是怎么样的呢,是否真正的处理过,如果遇到,你们应该怎么处理。 最后有相关的学习群,有兴趣可以加入。 开始 一、血泪教训:环境变量引发的真实灾难 1.1 …...

云原生周刊:深入探索 kube-scheduler-simulator
开源项目推荐 mcp-server-kubernetes mcp-server-kubernetes 是一个实现了模型上下文协议(MCP)的服务器,旨在通过自然语言与 K8s 集群进行交互。它支持连接到 K8s 集群,列出所有 Pod、服务、部署和节点,创建、描述、…...
3-Visual Studio 2022打包NET开发项目为安装包
引言 本文将上一期博文>>>门店管理系统开发<<<开发的项目打包为Windows安装包 一,安装扩展 安装此扩展:installer Projects 二,创建安装程序项目 创建项目 右键解决方案-添加-新建项目 选择setup Project项目 填写项目名…...

国内外网络安全政策动态(2025年3月)
▶︎ 1.《关于进一步加强智能网联汽车产品准入、召回及软件在线升级管理的通知》发布 3月1日,工业和信息化部、市场监管总局联合发布《关于进一步加强智能网联汽车产品准入、召回及软件在线升级管理的通知》(以下简称《通知》)。 该通知旨在…...

Kafka 和 Flink的讲解
一、Kafka:分布式消息队列 1. 核心概念 角色:Kafka 是一个分布式、高吞吐量的消息队列(Pub-Sub 模型),用于实时传输数据流。关键术语: Producer(生产者):发送数据的客户端(如传感器、应用日志)。Consumer(消费者):接收…...

已知Word内容格式固定,通过宏实现Word转Excel
文章目录 需求描述一、宏是什么?二、使用步骤1.启用开发工具2.VBA基础知识3.单个Word文件转为Excel4.批量将Word文件转为Excel文件 总结 需求描述 现在有多个Word文档,Word文档格式固定,假如Word内容分为单选题和多选题,每个题目…...

一文详解OpenGL环境搭建:Ubuntu20.4使用CLion配置OpenGL开发环境
在计算机图形学的广阔领域中,OpenGL作为行业标准的图形库,为开发者提供了强大的工具集来创建从简单的2D图形到复杂的3D世界。然而,对于初学者而言,配置一个合适的开发环境是迈向成功的第一步。本文将详细介绍如何在Ubuntu 20.04.3 LTS操作系统上搭建基于CLion的OpenGL开发环…...

Java面试黄金宝典41
1. IO 种类 定义 在 Java 里,IO(输入 / 输出)主要分为字节流和字符流这两种类型。字节流以字节为单位处理数据,适合处理二进制数据,像图片、音频、视频等;字符流以字符为单位处理数据,适用于处理文本数据。 要点 字节流处理二进制数据,字符流处理文本数据。字节流的基类…...

边缘计算革命:低功耗GPU在自动驾驶实时决策中的应用
边缘计算革命:低功耗GPU在自动驾驶实时决策中的应用 ——分析NVIDIA Jetson与华为昇腾的嵌入式方案差异 一、自动驾驶的实时决策挑战与边缘计算需求 自动驾驶系统需在30ms内完成环境感知、路径规划与车辆控制的全流程闭环。传统云端计算受限于网络延迟…...

【Java面试系列】Spring Boot中自动配置原理与自定义Starter开发实践详解 - 3-5年Java开发必备知识
【Java面试系列】Spring Boot中自动配置原理与自定义Starter开发实践详解 - 3-5年Java开发必备知识 引言 Spring Boot作为Java生态中最流行的框架之一,其自动配置机制和Starter开发是面试中的高频考点。对于3-5年经验的Java开发者来说,深入理解这些原理…...

MySQL的子查询
一、前言 MySQL 子查询是指嵌套在其他 SQL 语句(如 SELECT、WHERE、FROM 等)内部的查询。用于辅助主查询完成复杂的数据筛选或计算。 二、子查询分类 标量子查询 描述:返回 单行单列(一个值),常用于比较运…...

SpringDoc【使用详解】
SpringDoc使用详解 一、何为SpringDoc二、概念解释三、SpringDoc使用2.1简单集成2.2 配置SpringDoc2.2.1 yml方式配置2.2.2配置文档信息 2.3配置文档分组2.4使用注解2.4.1 Tag2.4.2 Operation2.4.3 Schema2.4.4 NotNull2.4.5 Parameter2.4.6 Parameters2.4.7 ApiResponses 和Ap…...

Redis持久化 | RDB AOF | 常见问题
目录 RDB(Redis DataBase) 给什么内存数据做快照——(全量) 触发机制 RDB文件生成的时候会阻塞主线程吗? 关闭持久化命令 bgsave执行流程 RDB文件怎么配置?有哪些优缺点 优点: 缺点&am…...

判断矩阵A是否可以相似对角化
【例题1】 【例题2】...

React 列表渲染
开发环境:Reacttsantd 你可能经常需要通过 JavaScript 的数组方法 来操作数组中的数据,从而将一个数据集渲染成多个相似的组件。在这篇文章中,你将学会如何在 React 中使用 filter() 筛选需要渲染的组件和使用 map() 把数组转换成组件数组。 …...
面向对象--封装(7)终章 C#内部类和分部类、密封类)
C#核心学习(八)面向对象--封装(7)终章 C#内部类和分部类、密封类
目录 一、内部类(Inner Class) 1. 什么是内部类? 2. 内部类的作用 3. 如何定义内部类? 4. 常见应用场景 二、分部类(Partial Class) 1. 什么是分部类? 2. 分部类的写法 3.…...

[ctfshow web入门] web25
信息收集 要想拿到flag,需要突破两层if。 解题 第一个if 传入r0,拿到mt_rand的值,由于每一次访问都会重新设置种子,所以每一次访问都是一样的随机数。 所以我们的r mt_rand-显示的值 1799250188 r1799250188就可以突破第一…...

局域网访问 Redis 方法
局域网访问 Redis 方法 默认情况下,Redis 只允许本机 (127.0.0.1) 访问。如果你想让局域网中的其他设备访问 Redis,需要 修改 Redis 配置,并确保 防火墙放行端口。 方法 1:修改 Redis 配置 1. 修改 redis.conf(或 me…...

oracle 索引失效
在 Oracle 11g 中,索引失效的常见原因包括函数修改列、隐式类型转换、统计信息过时等,解决方法需结合版本特性(如虚拟列、索引跳跃扫描)。通过执行计划分析、统计信息维护和合理使用提示(Hints),…...

