蓝桥杯刷题--宝石组合
在一个神秘的森林里,住着一个小精灵名叫小蓝。有一天,他偶然发现了一个隐藏在树洞里的宝藏,里面装满了闪烁着美丽光芒的宝石。这些宝石都有着不同的颜色和形状,但最引人注目的是它们各自独特的 “闪亮度” 属性。每颗宝石都有一个与生俱来的特殊能力,可以发出不同强度的闪光。小蓝共找到了 N 枚宝石,第 i 枚宝石的 “闪亮度” 属性值为 HiHi,小蓝将会从这 N 枚宝石中选出三枚进行组合,组合之后的精美程度SS 可以用以下公式来衡量:

其中 LCM 表示的是最小公倍数函数。
小蓝想要使得三枚宝石组合后的精美程度 S 尽可能的高,请你帮他找出精美程度最高的方案。如果存在多个方案 S 值相同,优先选择按照 H 值升序排列后字典序最小的方案。
输入格式
第一行包含一个整数 N 表示宝石个数。
第二行包含 N 个整数表示 N 个宝石的 “闪亮度”。
输出格式
输出一行包含三个整数表示满足条件的三枚宝石的 “闪亮度”。
思路
- 统计每个闪亮度出现的次数,存到cnt中。
- 从大到小枚举最大的gcd。在cnt中找它的倍数,累加个数并添到ans数组中。当个数大于等于3时,直接输出ans的值。
- 注意ans数组创建的时机,是每枚举一个gcd然后创建一个ans。
for(int i = max_a;i >= 1;i--){int cnt = 0; vector<int> ans;for(int j = i;j <= max_a;j+=i){//}化简题目思路
p都是底数,a b c 是指数
- 设Ha=p1a1p2a2⋯pnan,Hb=p1b1p2b2⋯pnbn,Hc=p1c1p2c2⋯pncn(分解质因数形式)
根据最小公倍数的质因数求法:对于两个数m=p1x1p2x2⋯pnxn,n=p1y1p2y2⋯pnyn ,LCM(m,n)=p1max(x1,y1)p2max(x2,y2)⋯pnmax(xn,yn) 。- LCM(Ha,Hb)=p1max(a1,b1)p2max(a2,b2)⋯pnmax(an,bn) ;
- LCM(Ha,Hc)=p1max(a1,c1)p2max(a2,c2)⋯pnmax(an,cn) ;
- LCM(Hb,Hc)=p1max(b1,c1)p2max(b2,c2)⋯pnmax(bn,cn) ;
- LCM(Ha,Hb,Hc)=p1max(a1,b1,c1)p2max(a2,b2,c2)⋯pnmax(an,bn,cn) 。
- HaHbHc=p1a1+b1+c1p2a2+b2+c2⋯pnan+bn+cn 。
- 分析分子分母中质因数的指数关系
对于质因数pi :- 分子中pi的指数为ai+bi+ci+max(ai,bi,ci) 。
- 分母中pi的指数为max(ai,bi)+max(ai,ci)+max(bi,ci) 。
通过分析指数大小关系(分多种情况讨论ai,bi,ci的大小顺序,如ai≥bi≥ci 时:分子指数为ai+bi+ci+ai,分母指数为ai+ai+bi ,相减得ci ;其他大小顺序情况类似分析 ),可以发现分子分母相除后,对于每个质因数pi ,化简后指数为gcd(ai,bi,ci)(gcd表示最大公约数)。 - 所以S=gcd(Ha,Hb,Hc) 。
最终答案
#include <iostream>
//#include <bits/stdc++.h>
#include <vector>
#include <unordered_map>
using namespace std;int main()
{// 请在此输入您的代码ios::sync_with_stdio(false);cin.tie(nullptr);int n; cin >> n;int mp[500100] = {0};int max_a = 0;for(int i = 0;i < n;i++){int a; cin >> a;mp[a]++;if(a > max_a) max_a = a;}for(int i = max_a;i >= 1;i--){int cnt = 0; vector<int> ans;for(int j = i;j <= max_a;j+=i){if(mp[j]){cnt += mp[j];for(int k = 0;k < mp[j] && ans.size() < 3;k++){ans.push_back(j);}if(cnt >= 3){for(int l = 0;l < 3;l++){cout << ans[l] << " ";}return 0;}}}}return 0;
}相关文章:

蓝桥杯刷题--宝石组合
在一个神秘的森林里,住着一个小精灵名叫小蓝。有一天,他偶然发现了一个隐藏在树洞里的宝藏,里面装满了闪烁着美丽光芒的宝石。这些宝石都有着不同的颜色和形状,但最引人注目的是它们各自独特的 “闪亮度” 属性。每颗宝石都有一个…...

红宝书第三十一讲:通俗易懂的包管理器指南:npm 与 Yarn
红宝书第三十一讲:通俗易懂的包管理器指南:npm 与 Yarn 资料取自《JavaScript高级程序设计(第5版)》。 查看总目录:红宝书学习大纲 一、基础概念 包管理器:帮你自动下载和管理第三方代码库(如…...

进程状态的转换
进程处于运行态时,它必须已获得所需的资源,在运行结束后就撤销。只有在时间片到或出现了比现在进程优先级更高的进程时才转变成就绪态。 就绪 → 运行 触发条件:进程被调度器选中(如时间片轮转或优先级调度&…...

SpringAOP新链浅析
前言 在复现CCSSSC软件攻防赛的时候发现需要打SpringAOP链子,于是跟着前人的文章自己动手调试了一下 参考了大佬的文章 https://gsbp0.github.io/post/springaop/#%E6%B5%81%E7%A8%8B https://mp.weixin.qq.com/s/oQ1mFohc332v8U1yA7RaMQ 正文 依赖于Spring-AO…...

【动手学深度学习】现代卷积神经网络:ALexNet
【动手学深度学习】现代卷积神经网络:ALexNet 1,ALexNet简介2,AlexNet和LeNet的对比3, AlexNet模型详细设计4,AlexNet采用ReLU激活函数4.1,ReLU激活函数4.2,sigmoid激活函数4.3,为什…...

PyTorch深度学习框架60天进阶学习计划 - 第37天:元学习框架
PyTorch深度学习框架60天进阶学习计划 - 第37天:元学习框架 嘿,朋友们!欢迎来到我们PyTorch进阶之旅的第37天。今天我们将深入探索一个非常有趣且强大的领域——元学习(Meta-Learning),也被称为"学会学习"(Learning to…...

【中检在线-注册安全分析报告】
前言 由于网站注册入口容易被黑客攻击,存在如下安全问题: 1. 暴力破解密码,造成用户信息泄露 2. 短信盗刷的安全问题,影响业务及导致用户投诉 3. 带来经济损失,尤其是后付费客户,风险巨大,造…...

UE5 运行时动态将玩家手部模型设置为相机的子物体
在编辑器里,我们虽然可以手动添加相机,但是无法将网格体设置为相机的子物体,只能将相机设置为网格体的子物体 但是为了使用方便,我们希望将网格体设置为相机的子物体,这样我们直接旋转相机就可以旋转网格体࿰…...

EasyExcel-一款好用的excel生成工具
EasyExcel是一款处理excel的工具类,主要特点如下(官方): 特点 高性能读写:FastExcel 专注于性能优化,能够高效处理大规模的 Excel 数据。相比一些传统的 Excel 处理库,它能显著降低内存占用。…...

WEB攻防-Java安全JNDIRMILDAP五大不安全组件RCE执行不出网不回显
目录 1. RCE执行-5大类函数调用 1.1 Runtime方式 1.2 Groovy执行命令 1.3 脚本引擎代码注入 1.4 ProcessImpl 1.5 ProcessBuilder 2. JNDI注入(RCE)-RMI&LDAP&高版本 2.1 RMI服务中的JNDI注入场景 2.2 LDAP服务中的JNDI注入场景 攻击路径示例&#…...

UML组件图
一、UML 组件图 组件图(Component Diagram)主要用于描述系统的物理结构,用于展示可独立部署的软件模块(如微服务、动态链接库、API网关)及其交互关系。组件图中的主要元素包括: 组件(Component…...

DrissionPage移动端自动化:从H5到原生App的跨界测试
一、移动端自动化测试的挑战与机遇 移动端测试面临多维度挑战: 设备碎片化:Android/iOS版本、屏幕分辨率差异 混合应用架构:H5页面与原生组件的深度耦合 交互复杂性:多点触控、手势操作、传感器模拟 性能监控:内存…...

从 Excel 到你的表格应用:条件格式功能的嵌入实践指南
一、引言 在日常工作中,面对海量数据时,如何快速识别关键信息、发现数据趋势或异常值,是每个数据分析师面临的挑战。Excel的条件格式功能通过自动化的视觉标记,帮助用户轻松应对这一难题。 本文将详细介绍条件格式的应用场景&am…...

redis 和 MongoDB都可以存储键值对,并且值可以是复杂json,用完整例子分别展示说明两者在存储json键值对上的使用对比
Redis 存储 JSON 键值对示例 存储操作: // 存储用户信息(键:user:1001,值:JSON对象) SET user:1001 {"name":"Alice", "age":30, "address":"New York&quo…...

SQLI打靶
文章目录 一、DVWA0. Mysql与Mariasql1. 单/双引号 - 十六进制编码绕过**原理:** 2. limit 1的绕过3. 参数化查询绕过一、介绍二、PDO是一种PHP实现参数化查询的机制 三、预编译绕过 之 结构化参数 4. 反自动化手段 之 Anti-CSRF token静态:动态…...

STM32单片机入门学习——第22节: [7-2] AD单通道AD多通道
写这个文章是用来学习的,记录一下我的学习过程。希望我能一直坚持下去,我只是一个小白,只是想好好学习,我知道这会很难,但我还是想去做! 本文写于:2025.04.07 STM32开发板学习——第22节: [7-2] AD单通道&AD多通道 前言开发板说明引用解…...

python基础语法1:输入输出
1. 输出 (Output) 1.1 print() 基础 Python 使用 print() 函数向控制台输出内容。 # 输出字符串 print("Hello, World!") # 输出多个值(自动用空格分隔) print("Name:", "Alice", "Age:", 25) # 修改分隔符&…...

对Android中zygote的理解
1. Zygote的作用 Zygote是Android系统的核心进程,核心作用可归纳为以下三点: 核心作用详细说明进程孵化器作为所有应用进程的父进程,通过fork快速创建新进程(避免重复初始化虚拟机)。(system server也由z…...

【Survival Analysis】【机器学习】【1】
前言: 今年在做的一个博士课题项目,主要是利用病人的数据,训练出一个AI模型,做因果分析, 以及个性化治疗。自己一直是做通讯AI方向的,这个系列主要参考卡梅隆大学的教程,以及临床医生的角度 了…...

WebShell详解:原理、分类、攻击与防御
目录 一、WebShell的定义与核心概念 二、WebShell的分类 三、WebShell的攻击原理与常见手法 1. 攻击原理 2. 常见攻击路径 四、WebShell的危害 五、防御与检测策略 六、总结 一、WebShell的定义与核心概念 WebShell是一种以ASP、PHP、JSP等网页脚本形式存在的恶…...

JavaScript---原型和原型链
目录 一、引用类型皆为对象 二、原型和原型链是什么 三、__proto__与prototype 总结 四、原型链顶层 五、constructor 六、函数对象的原型链 一、引用类型皆为对象 原型和原型链都是来源于对象而服务于对象: JavaScript中一切引用类型都是对象,…...

离散数学问题集--问题5.9
问题 5.9 综合了计算机组成原理、数字逻辑和离散数学中的关键概念,旨在帮助学生理解二进制算术运算的硬件实现、逻辑门与算术运算的关系,以及如何使用数学方法来验证数字系统的正确性。它强调了从规范到实现再到验证的完整过程。 思想 函数抽象…...

手游防DDoS攻击SDK接入
在手游中集成防DDoS攻击SDK是抵御流量型和应用层攻击的核心手段之一。以下从SDK选型、接入流程、防护策略优化三个维度提供完整指南,并附关键代码示例: 一、SDK选型与核心能力对比 服务商优势劣势适用场景…...

Java—HTML:CSS选择器
今天我要介绍的知识点内容是Java HTML中的CSS选择器; CSS选择器用于定位HTML元素并为其添加样式。它允许我们控制网页的颜色、字体、布局和其他视觉元素。通过分离内容与样式。 下面我将介绍CSS中选择器的使用,并作举例说明; 选择器基本语…...

如何将/dev/ubuntu-vg/lv-data的空间扩展到/dev/ubuntu-vg/ubuntu-lv的空间上
要将 /dev/ubuntu-vg/lv-data 的空间扩展到 /dev/ubuntu-vg/ubuntu-lv 上,实际上是将 lv-data 的空间释放出来,并将其分配给 ubuntu-lv。以下是详细的步骤和操作说明: 已知信息 你有两个逻辑卷: /dev/ubuntu-vg/lv-data/dev/ubun…...

SSM阶段性总结
0 Pojo类 前端给后端:DTO 后端给前端:VO 数据库:PO/VO 业务处理逻辑:BO 统称pojo 1 代理模式 实现静态代理: 1定义接口2实现类3写一个静态代理类4这样在调用时就可以使用这个静态代理类来实现某些功能 实现动态代…...
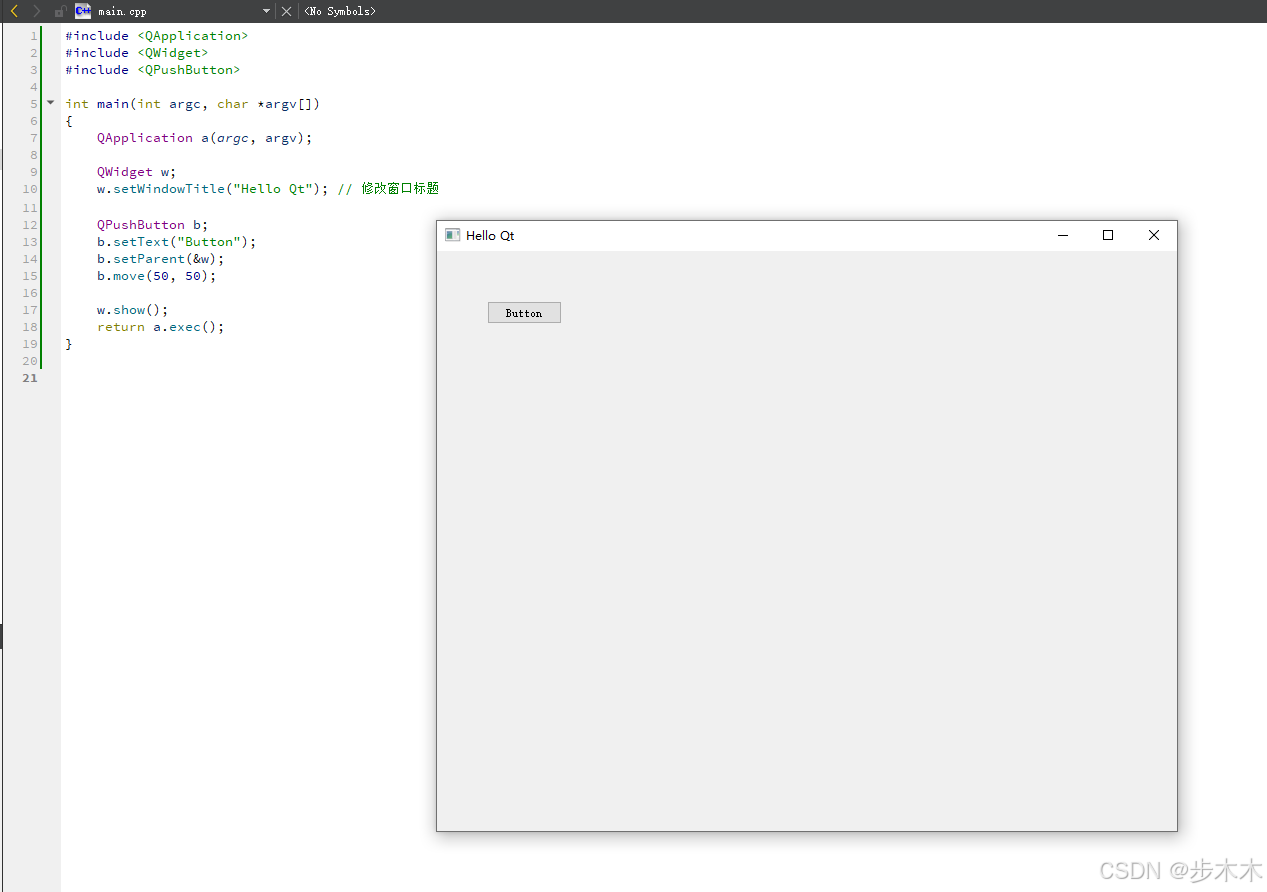
Qt 5.14.2入门(一)写个Hello Qt!程序
目录 参考链接:一、新建项目二、直接运行三、修改代码增加窗口内容1、Qt 显示一个 QLabel 标签控件窗口2、添加按键 参考链接: Qt5教程(一):Hello World 程序 Qt 编程指南 一、新建项目 1、新建一个项目(…...

Jmeter分布式测试启动
代理客户端配置 打开jmeter.properties文件,取消注释并设置端口(如server_port1099), 并添加server.rmi.ssl.disabletrue禁用SSL加密。 (Linux系统)修改jmeter-server文件中的RMI_HOST_DEF为代理机实际IP。…...

redis itheima
缓存问题 核心是如何避免大量请求到达数据库 缓存穿透 既不存在于 redis,也不存在于 mysql 的key,被重复请求 public Result queryById(Long id) {String key CACHE_SHOP_KEYid;// 1. redis & mysqlString shopJson stringRedisTemplate.opsFo…...

mysql 执行计划中eq_ref是什么意思?
在 MySQL 的执行计划中,eq_ref 是一种连接类型(type),表示查询优化器在使用**主键(PRIMARY KEY)或唯一索引(UNIQUE INDEX)**进行等值匹配()时,对表…...
