KF V.S. GM-PHD
在计算机视觉的多目标跟踪(MOT)任务中,卡尔曼滤波(KF)和高斯混合概率假设密度(GM-PHD)滤波器是两种经典的状态估计方法,但它们的原理和应用场景存在显著差异。以下是两者的核心机制和对比:
1. 卡尔曼滤波(KF)
核心思想
• 状态估计:基于线性动态模型和高斯噪声假设,通过“预测-更新”循环迭代估计目标的状态(如位置、速度)。
• 恒定速度模型(CV模型):假设目标在短时间内运动速度恒定,适用于简单运动场景。
工作流程(以目标跟踪为例)
-
预测(Predict):
• 根据上一时刻的状态 x k − 1 \mathbf{x}_{k-1} xk−1和状态转移矩阵 F \mathbf{F} F,预测当前状态 x k − \mathbf{x}_k^- xk−和协方差 P k − \mathbf{P}_k^- Pk−。
• 例如:
x k − = F x k − 1 , F = [ 1 0 Δ t 0 0 1 0 Δ t 0 0 1 0 0 0 0 1 ] \mathbf{x}_k^- = \mathbf{F} \mathbf{x}_{k-1}, \quad \mathbf{F} = \begin{bmatrix} 1 & 0 & \Delta t & 0 \\ 0 & 1 & 0 & \Delta t \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} xk−=Fxk−1,F= 10000100Δt0100Δt01
(状态向量通常为 x = [ x , y , v x , v y ] ⊤ \mathbf{x} = [x, y, v_x, v_y]^\top x=[x,y,vx,vy]⊤, Δ t \Delta t Δt为时间间隔) -
更新(Update):
• 将预测状态与当前帧的检测结果(观测 z k \mathbf{z}_k zk)融合,通过卡尔曼增益 K \mathbf{K} K修正状态和协方差。
• 更新公式:
x k = x k − + K ( z k − H x k − ) \mathbf{x}_k = \mathbf{x}_k^- + \mathbf{K}(\mathbf{z}_k - \mathbf{H} \mathbf{x}_k^-) xk=xk−+K(zk−Hxk−)
( H \mathbf{H} H为观测矩阵,将状态映射到观测空间) -
数据关联:
• 通常与匈牙利算法或IoU匹配结合,将检测框与预测状态关联。
优点
• 计算高效,适合实时系统。
• 对线性高斯运动模型表现稳定。
局限性
• 依赖线性模型,难以处理复杂运动(如急转弯)。
• 需手动设计状态向量和噪声参数。
2. 高斯混合概率假设密度(GM-PHD)滤波器
核心思想
• 多目标贝叶斯滤波:直接估计所有目标的联合概率密度(PHD),避免显式数据关联。
• 随机有限集(RFS):将目标和观测建模为随机集合,处理目标出现、消失和杂波。
工作流程
-
预测步骤:
• 根据上一时刻的PHD(高斯混合形式)和运动模型,预测当前PHD。
• 例如:
D k ∣ k − 1 ( x ) = ∑ i w k − 1 ( i ) N ( x ; F μ k − 1 ( i ) , Q + F P k − 1 ( i ) F ⊤ ) D_{k|k-1}(\mathbf{x}) = \sum_{i} w_{k-1}^{(i)} \mathcal{N}(\mathbf{x}; \mathbf{F} \mathbf{\mu}_{k-1}^{(i)}, \mathbf{Q} + \mathbf{F} \mathbf{P}_{k-1}^{(i)} \mathbf{F}^\top) Dk∣k−1(x)=i∑wk−1(i)N(x;Fμk−1(i),Q+FPk−1(i)F⊤)
( w k − 1 ( i ) w_{k-1}^{(i)} wk−1(i)为权重, Q \mathbf{Q} Q为过程噪声) -
更新步骤:
• 将当前帧的观测 z k \mathbf{z}_k zk与预测PHD融合,计算后验PHD。
• 更新公式(考虑漏检和杂波):
D k ( x ) = ( 1 − p D ) D k ∣ k − 1 ( x ) + ∑ z ∈ Z k p D D k ∣ k − 1 ( x ) g ( z ∣ x ) λ c ( z ) + ∫ p D g ( z ∣ ξ ) D k ∣ k − 1 ( ξ ) d ξ D_k(\mathbf{x}) = (1 - p_D) D_{k|k-1}(\mathbf{x}) + \sum_{\mathbf{z} \in \mathbf{Z}_k} \frac{p_D D_{k|k-1}(\mathbf{x}) g(\mathbf{z}|\mathbf{x})}{\lambda_c(\mathbf{z}) + \int p_D g(\mathbf{z}|\mathbf{\xi}) D_{k|k-1}(\mathbf{\xi}) d\mathbf{\xi}} Dk(x)=(1−pD)Dk∣k−1(x)+z∈Zk∑λc(z)+∫pDg(z∣ξ)Dk∣k−1(ξ)dξpDDk∣k−1(x)g(z∣x)
( p D p_D pD为检测概率, λ c \lambda_c λc为杂波强度) -
目标提取:
• 从后验PHD中提取高斯分量,保留权重大于阈值的分量作为目标状态估计。
优点
• 自动处理目标数量的变化(新生、消失)。
• 无需显式数据关联,适合高杂波场景。
局限性
• 计算复杂度高于KF(尤其高斯分量多时)。
• 需调参(如杂波强度、检测概率)。
3. 对比总结
| 特性 | 卡尔曼滤波(KF) | GM-PHD滤波器 |
|---|---|---|
| 适用场景 | 线性运动、目标数量固定 | 目标数量动态变化、高杂波环境 |
| 数据关联 | 需显式匹配(如匈牙利算法) | 隐式处理(通过PHD融合) |
| 计算效率 | 高效(适合实时) | 较高(高斯分量多时慢) |
| 参数依赖 | 运动模型、噪声协方差 | 杂波模型、检测概率 |
| 典型应用 | SORT、DeepSORT | MOT中的杂波场景(如雷达跟踪) |
4. 现代改进与联合方法
• KF的扩展:
• EKF/UKF:处理非线性运动(如转弯模型)。
• 自适应KF:动态调整噪声参数。
• GM-PHD的改进:
• LMB/PHD:结合标签管理,避免ID切换。
• 联合检测跟踪(如FairMOT、CenterTrack):
• 将检测、运动估计、关联模型端到端训练,平衡精度与效率。
相关文章:

KF V.S. GM-PHD
在计算机视觉的多目标跟踪(MOT)任务中,卡尔曼滤波(KF)和高斯混合概率假设密度(GM-PHD)滤波器是两种经典的状态估计方法,但它们的原理和应用场景存在显著差异。以下是两者的核心机制和…...

numpy.ma.masked_where:屏蔽满足条件的数组
1.函数功能 屏蔽满足条件的数组内容,返回值为掩码数组 2.语法结构 np.ma.masked_where(condition, a, copyTrue)3. 参数 参数含义condition屏蔽条件a要操作的数组copy布尔值,取值为True时,结果复制数组(原始数据不变),否则返回…...

python ftplib 上传文件名 乱码的解决办法
公司安排我用RPA把各电商平台昨天直播和视频相关的曝光、销售等数据下载下来,我用rpa基本一个星期完成了,最后用影刀RPA自带的ftp文件上传工具,都指定的ftp服务器上,用RPA上传后,文件名都是乱码,默认RPA内嵌…...

【解决】bartender软件换网之后神秘变慢
下的山寨版本bartender软件,用着一直都挺好,结果一次换网之后,启动,排版,打印各种动作都要转个几分钟才行,非常奇怪。直接说解决过程。 首先联想网络没有动以及脱机的时候,都没有这个问题。那么…...

Python小程序 - 文件处理3:正则表达式
正则表达式:文本年鉴表。遗留的问题很多。。。用AI再想想 需求:读入txt文件,过滤文件有关年记录 0)读入txt文件 1)以“。”,中文句号,为界区分一句,最小统计单位 2)年格…...
)
swift菜鸟教程11-12(数组与字典)
一个朴实无华的目录 今日学习内容:1.Swift 数组1.1创建数组1.2访问数组1.3修改数组使用 append() 方法或者赋值运算符 在数组末尾添加元素通过索引修改数组元素的值: 1.4遍历数组 使用for-in循环同时需要每个数据项的值和索引值 1.5合并数组1.6count 属…...

[福游宝——AI智能旅游信息查询平台]全栈AI项目-阶段二:聊天咨询业务组件开发
简言 本项目旨在构建一个以AI智能体为核心的福建省旅游信息查询系统,聚焦景点推荐、路线规划、交通天气查询等功能,为游客提供智能化、便捷化的旅游信息服务。项目采用前后端分离架构,前端基于Vite TypeScript Vue3技术栈,搭配…...

迷你世界脚本之容器接口:WorldContainer
容器接口:WorldContainer 彼得兔 更新时间: 2023-04-26 10:21:02 具体函数名及描述如下: 序号 函数名 函数描述 1 addFurnace(...) 新增熔炉 2 removeFurnace(...) 移除熔炉 3 checkFurnace(...) 检测是否为熔炉 4 getFurnaceHeatPerce…...
【教学类-102-11】蝴蝶外轮廓01——Python对黑白图片进行PS填充三种颜色+图案描边+图案填充白色+制作1图2图6图24图
背景需求: 用Python,对白色255背景的图片进行了透明化、制作点状或线段的描边裁剪线 【教学类-102-10】剪纸图案全套代码09——Python线条虚线优化版04(原图放大白背景)+制作1图2图6图24图-CSDN博客文章浏览阅读1k次,点赞27次,收藏8次。【教学类-102-10】剪纸图案全套代…...

MCP的另一面
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...

微信小程序 - swiper轮播图
官方文档:https://developers.weixin.qq.com/miniprogram/dev/component/swiper.html <swiper indicator-color"ivory" indicator-active-color"#d43c33" indicator-dots autoplay><swiper-item><image src"/images/banner…...

JSON-Server 极速入门教程
JSON-Server 入门教程 什么是 JSON-Server? JSON-Server 是一个零代码的 REST API 模拟工具,它可以在不到 30 秒的时间内为你创建一个完整的假 REST API。它非常适合前端开发者在没有后端支持的情况下进行开发和测试。 快速开始 1. 安装 首先&#…...

2025年第十六届蓝桥杯省赛C++ 研究生组真题
2025年第十六届蓝桥杯省赛C 研究生组真题 1.说明2.题目A:数位倍数(5分)3.题目B:IPv6(5分)4.题目C:变换数组(10分)5.题目D:最大数字(10分ÿ…...

七、自动化概念篇
自动化测试概念 自动化测试是把以人为驱动的测试行为转化为机器执行的一种过程。通常,在设计了测试用例并通过评审之后,由测试人员根据测试用例中描述的过程一步步执行测试,得到实际结果与期望结果的比较。在此过程中,为了节省人…...

【第43节】实验分析windows异常分发原理
目录 前言 一、异常处理大致流程图 二、实验一:分析 KiTrap03 三、实验二:分析CommonDispatchException 四、代码探究:分析 KiDispatchException 函数 五、代码探究:伪代码分析用户层KiUserExceptionDispatcher 前言 在Wind…...

如何在AMD MI300X 服务器上部署 DeepSeek R1模型?
DeepSeek-R1凭借其深度推理能力备受关注,在语言模型性能基准测试中可与顶级闭源模型匹敌。 AMD Instinct MI300X GPU可在单节点上高效运行新发布的DeepSeek-R1和V3模型。 用户通过SGLang优化,将MI300X的性能提升至初始版本的4倍,且更多优化将…...

RTX 5060 Ti 3DMark跑分首次流出:比RTX 4060 Ti快20%
快科技4月14日消息,根据VideoCardz拿到的数据,RTX 5060 Ti 16GB在3DMark的系列基准测试中,平均较上一代RTX 4060 Ti 16GB高出20%。 具体来看,RTX 5060 Ti 16GB在3DMark的测试中表现如下: TimeSpy(1440p&a…...

【STL】set
在 C C C S T L STL STL 标准库中, s e t set set 是一个关联式容器,表示一个集合,用于存储唯一元素的容器。 s e t set set 中的元素会自动按照一定的顺序排序(默认情况下是升序)。这意味着在 s e t set set 中不能…...

深入剖析C++中 String 类的模拟实现
目录 引言 一、基础框架搭建 成员变量与基本构造函数 析构函数 二、拷贝与赋值操作 深拷贝的拷贝构造函数 赋值运算符重载 三、字符串操作功能实现 获取字符串长度 字符串拼接 字符串比较 字符访问 四、迭代器相关实现(简单模拟) 迭代器类型…...

STL之priority_queue的用法与实现
目录 1. priority_queue的介绍 1.1. priority_queue的概念 1.2. priority_queue的特点 2. 仿函数 2.1. 仿函数的概念 2.2. 仿函数的应用 2.3 仿函数的灵活性 3. priority_queue的用法 4. 模拟实现priority_queue 4.1. 插入 4.2. 删除 5. 源码 priority_…...

深度学习中的数值稳定性处理详解:以SimCLR损失为例
文章目录 1. 问题背景SimCLR的原始公式 2. 数值溢出问题为什么会出现数值溢出?浮点数的表示范围 3. 数值稳定性处理方法核心思想数学推导 4. 代码实现分解代码与公式的对应关系 5. 具体数值示例示例:相似度矩阵方法1:直接计算exp(x)方法2&…...
散户使用算法交易怎么做?
智能算法交易是量化交易里面最常见的一种,也是大多数散户被套住的股票,想要解套,降低成本最直接有效的方式。但是往往这种波动速度小,担心速度跟不上的情况,我们就要叠加快速通道。 第一:算法交易的应用场…...

Docker详细使用
Docker详细使用 文章目录 Docker详细使用使用场景docker安装常用命令帮助启动类命令镜像命令网络命令容器命令compose(服务编排) 功能列表存储(挂载本地)介绍使用⽬录挂载卷映射 网络介绍使用 DockerfileCompose介绍使用 使用场景…...

mongodb 安装配置
1.官网下载地址:MongoDB Community Download | MongoDB 2.解压包安装:https://pan.baidu.com/s/1Er56twK9UfxoExuCPlJjhg 提取码: 26aj 3.配置环境: (1)mongodb安装包位置: (2)复…...

CSV文件中的中文乱码--UTF-8 with BOM
文章目录 1. 现象2. 原因3. BOM3.1 什么是BOM?3.2 BOM的作用3.3 特殊性 4. 如何解决乱码?4.1 手动设置格式4.2 自动设置格式4.2.1 Python如何设置:4.2.2 java如何设置 1. 现象 在使用了UTF-8格式编码之后,CSV文件在Excel中打开还…...
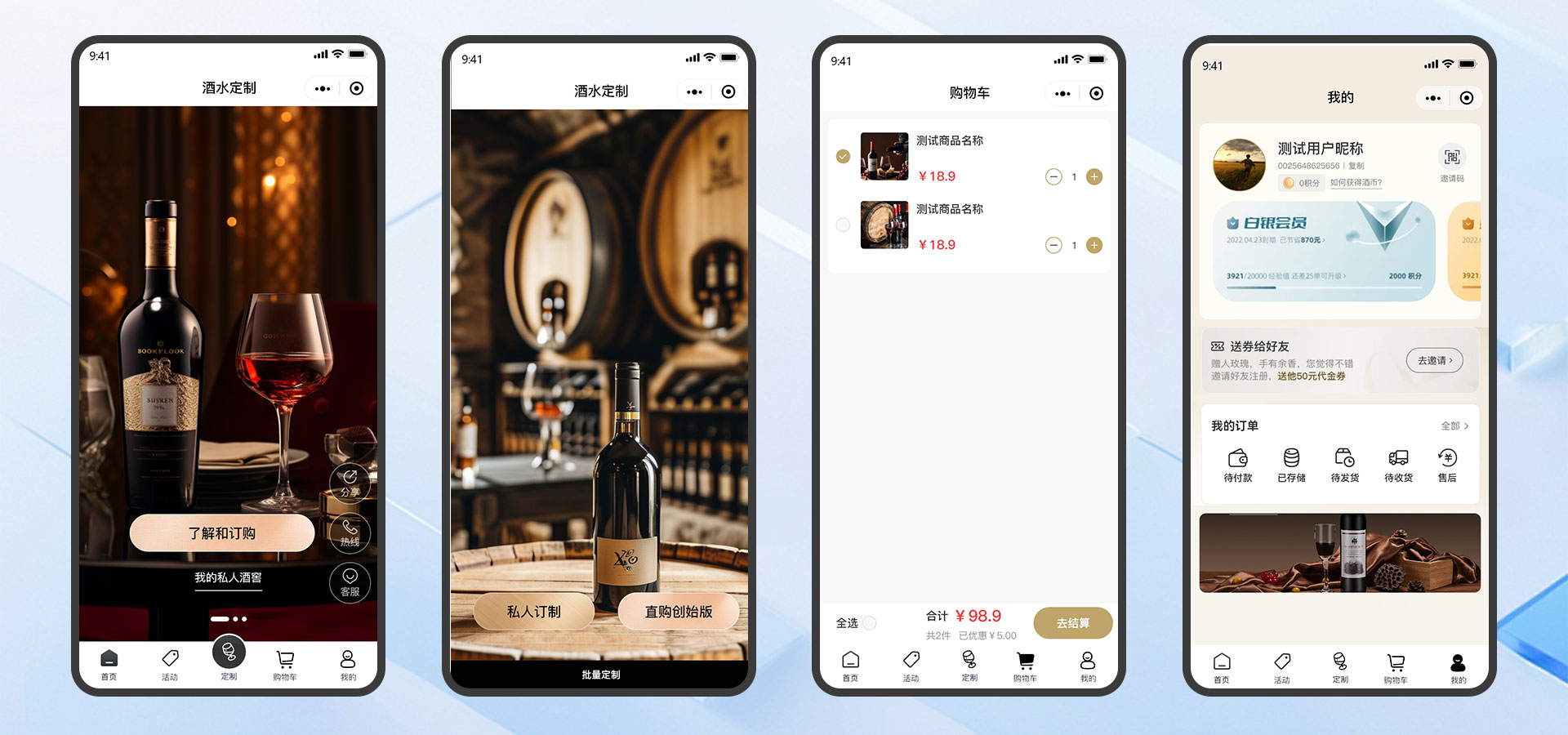
榕壹云酒水定制系统:基于THinKPHP+MySQL+UniApp打造数字化时代的个性化购酒新体验
数字化浪潮下的酒水定制新机遇 在消费升级与个性化需求崛起的背景下,传统酒水行业正面临数字化转型的迫切需求。为此,我们团队基于ThinkPHP+MySQL+UniApp技术栈,开发了一套榕壹云酒水定制系统,旨在通过数字化手段解决消费者个性化购酒痛点,为酒类品牌提供全链路数字化解决…...

Leetcode——137 260找出只出现一次的数
文章目录 找出只出现一次的数引入Leetcode 260Leetcode 137 找出只出现一次的数 对于数组中有一类题,即某些数据在数组中只出现一遍,需要我们找出,今天我们来看看这个类型的题。 引入 想必大家应该见过这么一道题: 现给定一个数…...

算法:定义一个数组的的陡峭值为:相邻两个元素之差的绝对值之和。
定义一个数组的的陡峭值为:相邻两个元素之差的绝对值之和。现在小红拿到了一个数组,她有多次询问,每次查询一段连续子数组的陡峭值。你能帮帮她吗? 连续子数组为从原数组中,连续的选择一段元素(可以全选、可以不选)得到的新数组。 输入描述 …...

uniapp自定义tabbar,根据角色动态显示不同tabbar,无闪动问题
🤵 作者:coderYYY 🧑 个人简介:前端程序媛,目前主攻web前端,后端辅助,其他技术知识也会偶尔分享🍀欢迎和我一起交流!🚀(评论和私信一般会回!!) 👉 个人专栏推荐:《前端项目教程以及代码》 ✨一、前言 这个需求在开发中还是很常见的,搜索了网络其他教程,…...

OpenTiny使用指南
最近项目里用到了一个新的组件库——OpenTiny,但是官方文档的使用指南的描述很复杂,花了一些时间尝试才正常使用。下面是一个使用步骤的描述,可放心食用: 一、安装 TinyVue 组件库同时支持 Vue 2.0 和 Vue 3.0 框架,…...
