【笔记】对抗训练-GAN
对抗训练-GAN
- 深度学习中 GAN 的对抗目标函数详解与最优解推导
- 一、GAN 的基本对抗目标函数
- 二、判别器与生成器的博弈目标
- 三、判别器的最优解推导
- 四、最优判别器的含义
- 五、总结
- 六、WGAN 的动机(为后续铺垫)
深度学习中 GAN 的对抗目标函数详解与最优解推导
生成对抗网络(GAN)是深度生成模型中的经典方法,其核心思想是两个网络之间的博弈:生成器 G G G 试图“伪造”样本,而判别器 D D D 尽力分辨真伪。本篇博客将从 GAN 的基本目标函数出发,逐步推导出判别器的最优形式,并分析其背后的数学含义。
一、GAN 的基本对抗目标函数
GAN 的原始目标是一个 min-max 游戏:
min G max D ( E x ∼ P r [ log D ( x ) ] + E z ∼ P z [ log ( 1 − D ( G ( z ) ) ) ] ) \min_G \max_D \left( \mathbb{E}_{x \sim P_r}[\log D(x)] + \mathbb{E}_{z \sim P_z}[\log(1 - D(G(z)))] \right) GminDmax(Ex∼Pr[logD(x)]+Ez∼Pz[log(1−D(G(z)))])
其中:
- P r ( x ) P_r(x) Pr(x) 表示真实数据的分布;
- P z ( z ) P_z(z) Pz(z) 是先验噪声分布(如高斯);
- G ( z ) G(z) G(z) 是生成器生成的假样本;
- D ( x ) D(x) D(x) 是判别器输出 x x x 为真实样本的概率。
二、判别器与生成器的博弈目标
-
判别器 D 的目标:让 D ( x ) D(x) D(x) 趋近于 1, D ( G ( z ) ) D(G(z)) D(G(z)) 趋近于 0,即正确分辨真实与生成样本。
对应目标函数为最大化:
E x ∼ P r [ log D ( x ) ] + E z ∼ P z [ log ( 1 − D ( G ( z ) ) ) ] \mathbb{E}_{x \sim P_r}[\log D(x)] + \mathbb{E}_{z \sim P_z}[\log(1 - D(G(z)))] Ex∼Pr[logD(x)]+Ez∼Pz[log(1−D(G(z)))]
-
生成器 G 的目标:生成样本让 D ( G ( z ) ) D(G(z)) D(G(z)) 尽量大,即“骗过”判别器。
对应目标函数为最小化:
E z ∼ P z [ log ( 1 − D ( G ( z ) ) ) ] \mathbb{E}_{z \sim P_z}[\log(1 - D(G(z)))] Ez∼Pz[log(1−D(G(z)))]
这是一个典型的零和对抗过程。
三、判别器的最优解推导
我们接下来推导:在固定生成器 G G G 的前提下,判别器 D D D 的最优形式是怎样的?
令目标函数为:
V ( D ) = ∫ x P r ( x ) log D ( x ) + P g ( x ) log ( 1 − D ( x ) ) d x V(D) = \int_x P_r(x) \log D(x) + P_g(x) \log(1 - D(x)) \, dx V(D)=∫xPr(x)logD(x)+Pg(x)log(1−D(x))dx
对每个 x x x,令:
f ( D ( x ) ) = P r ( x ) log D ( x ) + P g ( x ) log ( 1 − D ( x ) ) f(D(x)) = P_r(x) \log D(x) + P_g(x) \log(1 - D(x)) f(D(x))=Pr(x)logD(x)+Pg(x)log(1−D(x))
对 D ( x ) D(x) D(x) 求导并令导数为 0:
d f d D ( x ) = P r ( x ) D ( x ) − P g ( x ) 1 − D ( x ) = 0 \frac{d f}{d D(x)} = \frac{P_r(x)}{D(x)} - \frac{P_g(x)}{1 - D(x)} = 0 dD(x)df=D(x)Pr(x)−1−D(x)Pg(x)=0
解得最优判别器为:
D ∗ ( x ) = P r ( x ) P r ( x ) + P g ( x ) D^*(x) = \frac{P_r(x)}{P_r(x) + P_g(x)} D∗(x)=Pr(x)+Pg(x)Pr(x)
四、最优判别器的含义
-
D ∗ ( x ) D^*(x) D∗(x) 的输出值反映了 样本 x x x 来自真实分布的概率。
- 如果 P r ( x ) = P g ( x ) P_r(x) = P_g(x) Pr(x)=Pg(x),则 D ∗ ( x ) = 1 2 D^*(x) = \frac{1}{2} D∗(x)=21;
- 如果 P r ( x ) ≫ P g ( x ) P_r(x) \gg P_g(x) Pr(x)≫Pg(x),则 D ∗ ( x ) ≈ 1 D^*(x) \approx 1 D∗(x)≈1;
- 如果 P g ( x ) ≫ P r ( x ) P_g(x) \gg P_r(x) Pg(x)≫Pr(x),则 D ∗ ( x ) ≈ 0 D^*(x) \approx 0 D∗(x)≈0。
-
将 D ∗ D^* D∗ 代入 GAN 原始目标函数:
V ( D ∗ ) = E x ∼ P r [ log D ∗ ( x ) ] + E x ∼ P g [ log ( 1 − D ∗ ( x ) ) ] V(D^*) = \mathbb{E}_{x \sim P_r}[\log D^*(x)] + \mathbb{E}_{x \sim P_g}[\log(1 - D^*(x))] V(D∗)=Ex∼Pr[logD∗(x)]+Ex∼Pg[log(1−D∗(x))]
可推导出最终目标:
min G V ( D ∗ ) = − log 4 + 2 ⋅ JS ( P r ∥ P g ) \min_G V(D^*) = -\log 4 + 2 \cdot \text{JS}(P_r \parallel P_g) GminV(D∗)=−log4+2⋅JS(Pr∥Pg)
即:GAN 实质上是在最小化真实分布 P r P_r Pr 与生成分布 P g P_g Pg 之间的 Jensen-Shannon 散度。
五、总结
| 内容 | 含义 |
|---|---|
| D ∗ ( x ) = P r ( x ) P r ( x ) + P g ( x ) D^*(x) = \frac{P_r(x)}{P_r(x) + P_g(x)} D∗(x)=Pr(x)+Pg(x)Pr(x) | 判别器在每个样本点处的最优输出 |
| GAN 的优化目标 | 最小化 JS 散度 |
| 最优时的结果 | 当 P r = P g P_r = P_g Pr=Pg 时,GAN 达到最优, D ( x ) = 0.5 D(x)=0.5 D(x)=0.5,分不出真假 |
六、WGAN 的动机(为后续铺垫)
由于 Jensen-Shannon 散度在 P r P_r Pr 与 P g P_g Pg 没有交集时不连续(导致梯度消失),Wasserstein GAN(WGAN)改用 Wasserstein 距离替代 JS 散度,并要求判别器满足 1-Lipschitz 条件,这会在后续单独展开讲解。
相关文章:

【笔记】对抗训练-GAN
对抗训练-GAN 深度学习中 GAN 的对抗目标函数详解与最优解推导一、GAN 的基本对抗目标函数二、判别器与生成器的博弈目标三、判别器的最优解推导四、最优判别器的含义五、总结六、WGAN 的动机(为后续铺垫) 深度学习中 GAN 的对抗目标函数详解与最优解推导…...
安卓开发中数据存储之Room详解)
(二十三)安卓开发中数据存储之Room详解
在安卓开发中,Room 是一个强大的本地数据库解决方案,它是 Android Jetpack 的一部分,基于 SQLite 构建,提供了更高层次的抽象。Room 简化了数据库操作,减少了样板代码,同时支持与 LiveData 和 ViewModel 的…...

AIoT 智变浪潮演讲实录 | 刘浩然:让硬件会思考:边缘大模型网关助力硬件智能革新
4 月 2 日,由火山引擎与英特尔联合主办的 AIoT “智变浪潮”技术沙龙在深圳成功举行,活动聚焦 AI 硬件产业的技术落地与生态协同,吸引了芯片厂商、技术方案商、品牌方及投资机构代表等 700 多位嘉宾参会。 会上,火山引擎边缘智能高…...
【Windows】系统安全移除移动存储设备指南:告别「设备被占用」弹窗
Windows系统安全移除移动存储设备指南:告别「设备被占用」弹窗 解决移动硬盘和U盘正在被占用无法弹出 一、问题背景 使用Windows系统时,经常遇到移动硬盘/U盘弹出失败提示「设备正在使用中」,即使已关闭所有可见程序。本文将系统梳理已验证…...

C++运算符重载全面总结
C运算符重载全面总结 运算符重载是C中一项强大的特性,它允许程序员为自定义类型定义运算符的行为。以下是关于C运算符重载的详细总结: 一、基本概念 1. 什么是运算符重载 运算符重载是指为自定义类型(类或结构体)重新定义或重…...
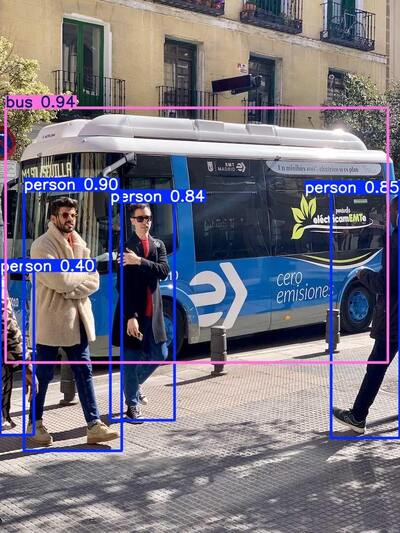
ArmSoM Sige5 CM5:RK3576 上 Ultralytics YOLOv11 边缘计算新标杆
在计算机视觉技术加速落地的今天,ArmSoM 正式宣布其基于 Rockchip RK3576 的旗舰产品 Sige5 开发板 和 CM5 核心板 全面支持 Ultralytics YOLOv11 模型的 RKNN 部署。这一突破标志着边缘计算领域迎来新一代高性能、低功耗的 AI 解决方案&am…...

【计算机网络】什么是路由?核心概念与实战详解
📌 引言 路由(Routing)是互联网的“导航系统”,负责将数据包从源设备精准送达目标设备。无论是浏览网页、发送消息还是视频通话,背后都依赖路由技术。本文将用通俗类比技术深度的方式,解析路由的核心机制。…...

【ubuntu】linux开机自启动
目录 开机自启动: /etc/rc.loacl system V 使用/etc/rc*.d/系统运行优先级 遇到的问题: 1. Linux 系统启动阶段概述 方法1:/etc/rc5.d/ 脚本延时日志 方法二:使用 udev 规则来触发脚本执行 开机自启动: /etc/…...

dnf install openssl失败的原因和解决办法
网上有很多编译OpenSSL源码(3.x版本)为RPM包的文章,这些文章在安装RPM包时都是执行rpm -ivh openssl-xxx.rpm --nodeps --force 这个命令能在缺少依赖包的情况下能强行执行安装 其实根据Centos的文档,安装RPM包一般是执行yum install或dnf install。后者…...

Java 在人工智能领域的突围:从企业级架构到边缘计算的技术革新
一、Java AI 的底层逻辑:从语言特性到生态重构 在 Python 占据 AI 开发主导地位的当下,Java 正通过技术重构实现突围。作为拥有 30 年企业级开发经验的编程语言,Java 的核心优势在于强类型安全、内存管理能力和分布式系统支持,这…...

操作系统导论——第19章 分页:快速地址转换(TLB)
使用分页作为核心机制来实现虚拟内存,可能会带来较高的性能开销。使用分页,就要将内存地址空间切分成大量固定大小的单元(页),并且需要记录这些单元的地址映射信息。因为这些映射信息一般存储在物理内存中,…...

计算机网络:流量控制与可靠传输机制
目录 基本概念 流量控制:别噎着啦! 可靠传输:快递必达服务 传输差错:现实中的意外 滑动窗口 基本概念 换句话说:批量发货排队验收 停止-等待协议 SW(发1份等1份) 超时重传:…...

SaaS、Paas、IaaS、MaaS、BaaS五大云计算服务模式
科普版:通俗理解五大云计算服务模式 1. SaaS(软件即服务) 一句话解释:像“租用公寓”,直接使用现成的软件,无需操心维护。 案例:使用钉钉办公、在网页版WPS编辑文档。服务提供商负责软件更新和…...

计算机网络 - 三次握手相关问题
通过一些问题来讨论 TCP 协议中的三次握手机制 说一下三次握手的大致过程?为什么需要三次握手?2 次不可以吗?第三次握手,可以携带数据吗?第二次呢?三次握手连接阶段,最后一次ACK包丢失…...

通过使用 include 语句加载并执行一个CMake脚本来引入第三方库
通过使用 include 语句加载并执行一个CMake脚本来引入第三方库 当项目中使用到第三方库时,可以通过使用 include 语句来加载并执行一个CMake脚本,在引入的CMake脚本中进行第三方库的下载、构建和库查找路径的设置等操作,以这种方式简化项目中…...

架构生命周期(高软57)
系列文章目录 架构生命周期 文章目录 系列文章目录前言一、软件架构是什么?二、软件架构的内容三、软件设计阶段四、构件总结 前言 本节讲明架构设计的架构生命周期概念。 一、软件架构是什么? 二、软件架构的内容 三、软件设计阶段 四、构件 总结 就…...

JMeter使用
1.简介 1.1 打开方式 ①点击bat,打开 ②添加JMeter系统环境变量,输⼊命令jmeter即可启动JMeter⼯具 1.2 配置 简体中文 放大字体 1.3 使用 ①添加线程组 ②创建http请求 2. 组件 2.1 线程组 控制JMeter将⽤于执⾏测试的线程数,也可以把⼀个线程理解为⼀个测…...

Ant Design Vue 表格复杂数据合并单元格
Ant Design Vue 表格复杂数据合并单元格 官方合并效果 官方示例 表头只支持列合并,使用 column 里的 colSpan 进行设置。 表格支持行/列合并,使用 render 里的单元格属性 colSpan 或者 rowSpan 设值为 0 时,设置的表格不会渲染。 <temp…...

Fiddler为什么可以看到一次HTTP请求数据?
1、作为代理服务器 Fiddler作为代理服务器,拦截了设备与互联网服务器之间的所有HTTP和HTTPS流量。当客户端(如浏览器)发送请求时,请求先到达Fiddler,然后由Fiddler转发到目标服务器;服务器的响应也会返回给…...

第十九讲 | XGBoost 与集成学习:精准高效的地学建模新范式
🟨 一、为什么要学习集成学习? 集成学习(Ensemble Learning) 是一种将多个弱学习器(如决策树)组合成一个强学习器的策略。它在地理学、生态学、遥感分类等领域表现尤为突出。 📌 应用优势&#…...

基于 GoFrame 框架的电子邮件发送实践:优势、特色与经验分享
1. 引言 如果你是一位有1-2年Go开发经验的后端开发者,可能已经熟悉了Go语言在性能和并发上的天然优势,也曾在项目中遇到过邮件发送的需求——无论是用户注册时的激活邮件、系统异常时的通知,还是营销活动中的批量促销邮件,邮件功…...

ECharts 如何实现柱状图悬停时,整个背景区域均可触发点击事件
1. 前言 ECharts 柱状图的点击事件默认仅响应柱子本身的点击,本文旨在实现整个背景区域均可触发点击事件 2. 实现思路 核心:全局监听 坐标判断 数据转换 通过 getZr() 监听整个画布点击,结合像素坐标判断是否在图表区域内通过 containPi…...

金融简单介绍及金融诈骗防范
在当今社会,金融学如同一股无形却强大的力量,深刻影响着我们生活的方方面面。无论是个人的日常收支、投资理财,还是国家的宏观经济调控,都与金融学紧密相连。 一、金融学的概念 金融学,简单来说,是研…...

cursor+高德MCP:制作一份旅游攻略
高德开放平台 | 高德地图API (amap.com) 1.注册成为开发者 2.进入控制台选择应用管理----->我的应用 3.新建应用 4.点击添加Key 5.在高德开发平台找到MCP的文档 6.按照快速接入的步骤,进行操作 一定要按照最新版的cursor, 如果之前已经安装旧的版本卸载掉重新安…...

软件版本命名规范Semantic Versioning
语义化版本控制(Semantic Versioning,简称 SemVer)是一种广泛采用的版本号管理规范,旨在通过版本号传达软件更新的性质和影响,帮助开发者和用户理解每次发布的变更内容 🔢 版本号结构 语义化版本号通常采…...

Uniapp: 大纲
目录 一、基础巩固1.1、Uniapp:下拉选择框ba-tree-picker1.2、Uniapp:确认框1.3、Uniapp:消息提示1.4、Uniapp:获取当前定位坐标 二、项目配置2.1、Uniapp:修改端口号2.2、Uniapp:本地存储 一、基础巩固 1.1、Uniapp:…...

Kubernetes控制平面组件:API Server Webhook 授权机制 详解
云原生学习路线导航页(持续更新中) kubernetes学习系列快捷链接 Kubernetes架构原则和对象设计(一)Kubernetes架构原则和对象设计(二)Kubernetes架构原则和对象设计(三)Kubernetes控…...

【KWDB 创作者计划】_产品技术解读_1
【KWDB 创作者计划】_产品技术解读_1 一、存储引擎:高性能混合存储架构1. 存储模型设计2. 存储压缩与编码3. 持久化策略二、KWDB 组件源码解析1. 核心模块分层架构2. 关键组件源码剖析三、KWDB 特性代码通读1. 实时分析能力(Real-Time OLAP)2. 混合负载隔离(HTAP)3. 智能索…...

Python Cookbook-6.2 定义常量
任务 你需要定义一些模块级别的变量(比如命名的常量),而且客户代码无法将其重新绑定。 解决方案 你可以把任何对象当做模块一样安装。将下列代码存为一个模块const.py,并放入你的Python的sys.path 指定的目录中: class _const(object):class ConstEr…...

【Python爬虫】简单案例介绍2
本文继续接着我的上一篇博客【Python爬虫】简单案例介绍1-CSDN博客 目录 跨页 3.2 环境准备 跨页 当对单个页面的结构有了清晰的认识并成功提取数据后,接下来就需要考虑页面之间的跨页问题。此时我们便迎来了下一个关键任务:如何实现跨页爬取…...
