剑指Offer(数据结构与算法面试题精讲)C++版——day12
剑指Offer(数据结构与算法面试题精讲)C++版——day12
- 题目一:小行星碰撞
- 题目二:每日温度
- 题目三:直方图最大矩形面积
- 附录:源码gitee仓库
题目一:小行星碰撞
题目:输入一个表示小行星的数组,数组中每个数字的绝对值表示小行星的大小,数字的正负号表示小行星运动的方向,正号表示向右飞行,负号表示向左飞行。如果两颗小行星相撞,那么体积较小的小行星将会爆炸最终消失,体积较大的小行星不受影响。如果相撞的两颗小行星大小相同,那么它们都会爆炸消失。飞行方向相同的小行星永远不会相撞。求最终剩下的小行星。例如,有6颗小行星[4, 5, -6, 4, 8, -5],如图6.2所示(箭头表示飞行的方向),它们相撞之后最终剩下3颗小行星[-6, 4, 8]。

由题意可知,这里我们可使用栈来实现,依次检查每个小行星的运动方向以及小行星大小,比如,这里拿[+4,+5,-6]三颗行星举例,由于-6的小行星比+4和+5行星大,那么由于-6行星和+4、+5两个行星一定会相撞,最后只剩下-6行星。如果使用栈结构来存储就能够很好的解决这个问题,一开始+4直接压入到栈中,然后遇到了+5由于不存在反向,于是同样压入栈中,遇到-6(待入栈元素)之后,由于与栈顶元素方向不一致,弹出栈顶元素,比较,发现栈顶元素应该被销毁,于是接着弹出直到这个待入栈元素要么消失,要么入栈,或者栈为空。通过这样的分析可以得到如下代码:
int getDirection(int number) {return number > 0 ? 1 : -1;
}
vector<int> getRemain(vector<int> arr) {stack<int> st;int top=0;for(int i=0,size=arr.size(); i<size; ++i) {if(st.empty()) {st.push(arr[i]);continue;} else {top=st.top();if(getDirection(top)==1&&getDirection(arr[i])==-1) {if(abs(top)>abs(arr[i])) {continue;} else if(arr[i]==top) {st.pop();} else {while(!st.empty()&&abs(top)<abs(arr[i])) {st.pop();if(st.empty()) {break;} else {top=st.top();}}if(st.empty()) {st.push(arr[i]);} else if(top==arr[i]) {st.pop();}}} else {st.push(arr[i]);}}}vector<int> result= {};while(!st.empty()) {result.push_back(st.top());st.pop();}return result;
}

题目二:每日温度
题目:输入一个数组,它的每个数字是某天的温度。请计算每天需要等几天才会出现更高的温度。例如,如果输入数组[35, 31, 33, 36, 34],那么输出为[3, 1, 1, 0, 0]。由于第1天的温度是35℃,要等3天才会出现更高的温度36℃,因此对应的输出为3。第4天的温度是36℃,后面没有更高的温度,它对应的输出是0。其他的以此类推。
这里存在一个关键问题,对于前面出现过的数据,无法知道后面还有几个数,无法判断距离更大气温的天数,比如[4,3,2,1,6],只有等到所有的数都获取之后才知道最终确认距离更高气温的天数。如果是使用暴力法,那么对于第i个数,最坏情况下需要遍历其后的(n-i)个数,这样最坏的时间复杂度为O(n^2)。
分析可以发现,对于示例数组[35,31,33,36,34],可以利用栈结构保存暂时没有确认距离更大的元素的下标,比如这里从左到右遍历,最开始遍历[35,31]都没有出现过更高气温,所以压入到栈中[0,1],接下来遍历到新元素[33],可以从栈取出栈顶元素判断,发现找到了一个更大的,用当前新来的元素的下标减去栈中元素的下标即可得到距离更大元素的下标。按照这样的方式就能够一次遍历拿到所有元素距离更大元素的个数了,最终得到代码如下:
vector<int> getRemainDays(vector<int> arr) {stack<int> st;int size=arr.size(),top=0;vector<int> result(size,0);for(int i=0; i<size; ++i) {if(st.empty()||arr[st.top()]>=arr[i]) {st.push(i);} else {top=st.top();while(arr[top]<arr[i]) {result[top]=i-top;st.pop();if(st.empty()) {break;} else {top=st.top();}}}}return result;
}

这题得思路比较巧妙,很值得积累。利用了栈去保留前面没有被计算出结果,然后再利用栈得特性在之后得运算中弹出栈中元素,利用已知数据推理出结果。这里得时间复杂度为O(n),因为在最坏情况下每个元素入栈一次,出栈一次。
题目三:直方图最大矩形面积
题目:直方图是由排列在同一基线上的相邻柱子组成的图形。输入一个由非负数组成的数组,数组中的数字是直方图中柱子的高。求直方图中最大矩形面积。假设直方图中柱子的宽都为1。例如,输入数组[3, 2, 5, 4, 6, 1, 4, 2],其对应的直方图如图6.3所示,该直方图中最大矩形面积为12,如阴影部分所示。

这道题似曾相识,应该也是leetcode上面的题目。这题如果先不考虑使用栈相关的数据结构,使用前面提到的双指针法是否可行呢,设置前后指针,一开始让前后两指针都指向第一个数,然后第一个数后移,移到一定程度之后前指针也后移。分析发现这个方法是不行的,因为前一个指针往前移的过程中可能矩形会缩小,不满足双指针适用条件。
这样不行那蛮力法呢,显然是可行的,双重遍历数组进行组合定界,比如锁定一组下标[min,max],然后矩形的面积就等于(max-min)*min{arr[min-max]},但是这样的事件复杂度太高了。
其实,这里有一个更加巧妙的方法——单调栈法。分析发现,对于每个矩形面积的计算,可以以当前扫描到的柱子作为基准,然后向该柱子左右两次查找比基准柱子矮的柱子,比如以下标为3的坐标为例(也就是数组中第一次出现的4),扫描两侧可以发现左侧更矮的柱子下标为1(也就是数组中第一次数显的2),右侧更矮的柱子下标为5(也就是数组中的1),从而可以得到以数值4为基准的最大矩形面积为4*(5-1-1)=12。
受到这一点的启发,我们可以得到一个非常巧妙的方法,现在的关键就在于为每个矩形左右两侧更矮的柱子定界,和前面题目2的方法类似,我们从左到右遍历数组(也就是这里矩形柱),构建一个柱子高度严格递增的矩形柱栈(为了方便获取柱子的高度和计算矩形宽度,这里和题目2一致存储下标),如果当前遍历的柱子比栈顶已有的柱子矮,那么说明当前栈顶柱子的左右下界都找到了,那么可以根据定界计算其最大矩形面积。如果当前遍历的柱子的高度比当前栈顶的柱子的高度高,那么直接入栈(以存储下标的形式)。最终得到如下代码:
int getMaxRectSquare(vector<int> arr) {stack<int> st;int result=0,size=arr.size(),top=0,height=0,width=0;for(int i=0; i<size; ++i) {while(!st.empty()&&arr[st.top()]>=arr[i]) {//构建一个严格递增的单调栈 height=arr[st.top()];st.pop();width=st.empty() ? i:(i-st.top()-1);if(width*height>result) {result=width*height;}}st.push(i);}while(!st.empty()) {top=st.top();height=arr[top];st.pop();width=st.empty()?arr.size():(arr.size()-st.top()-1);//左侧元素边界,否则取所有 if(width*height>result) {result=width*height;}}return result;
}

附录:源码gitee仓库
考虑到有些算法需要模拟数据,如果全部放进来代码显得过长,不利于聚焦在算法的核心思路上。于是把所有的代码整理到了开源仓库上,如果想要看详细模拟数据,可在开源仓库自取:【凌空暗羽/剑指offer-C++版手写代码】。
我是【Jerry说前后端】,本系列精心挑选的算法题目全部基于经典的《剑指 Offer(数据结构与算法面试题精讲)》。在如今竞争激烈的技术求职环境下,算法能力已成为前端开发岗位笔试考核的关键要点。通过深入钻研这一系列算法题,大家能够系统地积累算法知识和解题经验。每一道题目的分析与解答过程,都像是一把钥匙,为大家打开一扇通往高效编程思维的大门,帮助大家逐步提升自己在数据结构运用、算法设计与优化等方面的能力。
无论是即将踏入职场的应届毕业生,还是想要进一步提升自己技术水平的在职开发者,掌握扎实的算法知识都是提升竞争力的有力武器。希望大家能跟随我的步伐,在这个系列中不断学习、不断进步,为即将到来的前端笔试做好充分准备,顺利拿下心仪的工作机会!快来订阅吧,让我们一起开启这段算法学习之旅!
相关文章:

剑指Offer(数据结构与算法面试题精讲)C++版——day12
剑指Offer(数据结构与算法面试题精讲)C版——day12 题目一:小行星碰撞题目二:每日温度题目三:直方图最大矩形面积附录:源码gitee仓库 题目一:小行星碰撞 题目:输入一个表示小行星的数…...
(java)距离相等的条形码)
贪心算法(18)(java)距离相等的条形码
在一个仓库里,有一排条形码,其中第 i 个条形码为 barcodes[i]。 请你重新排列这些条形码,使其中任意两个相邻的条形码不能相等。 你可以返回任何满足该要求的答案,此题保证存在答案。 示例 1: 输入:barco…...
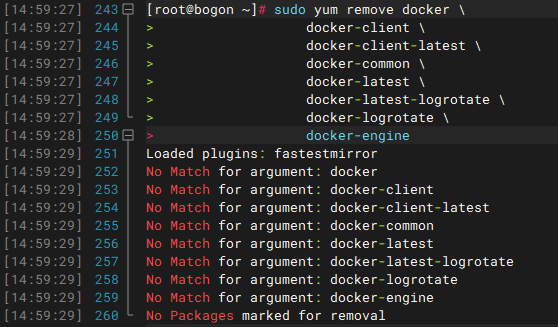
Docker学习笔记-docker安装、删除
一、在centOS 7中docker的默认安装目录 # Docker 主配置文件目录 ls /etc/docker# Docker 数据目录(镜像、容器、卷等) ls /var/lib/docker# Docker 可执行文件路径 which docker # 输出类似 /usr/bin/docker 二、docker文件目录说明 目录/文件用途/…...

【Python 开源】你的 Windows 关机助手——PyQt5 版定时关机工具
🖥️ 你的 Windows 关机助手——PyQt5 版定时关机工具 相关资源文件已经打包成EXE文件,可双击直接运行程序,且文章末尾已附上相关源码,以供大家学习交流,博主主页还有更多Python相关程序案例,秉着开源精神的…...

STM32 HAL库 ADC+TIM+DMA 3路 1S采样一次电压
一、引言 在很多嵌入式系统应用中,需要对多路模拟信号进行周期性采样,例如在工业控制、环境监测等领域。STM32F407 是一款高性能的微控制器,其丰富的外设资源可以方便地实现这样的功能。通过结合 ADC(模拟 - 数字转换器ÿ…...

汉诺塔问题——用贪心算法解决
目录 一:起源 二:问题描述 三:规律 三:解决方案 递归算法 四:代码实现 复杂度分析 一:起源 汉诺塔(Tower of Hanoi)问题起源于一个印度的古老传说。在世界中心贝拿勒斯&#…...

【Python爬虫】简单介绍
目录 一、基本概念 1.1 什么是爬虫 1.2 Python为什么适合爬虫 1.3 Python爬虫应用领域 (1)数据采集与分析 市场调研 学术研究 (2)内容聚合与推荐 新闻聚合 视频内容聚合 (3)金融领域 股票数据获…...

使用MCP服务通过自然语言操作数据库(vscode+cline版本)
使用MCP服务操纵数据库(vscodecline版本) 本文主要介绍,在vscode中使用cline插件调用deepseek模型,通过MCP服务器 使用自然语言去操作指定数据库。本文使用的是以己经创建号的珠海航展数据库。 理解MCP服务: MCP(Model Context…...

Vue 3 + TypeScript 实现一个多语言国际化组件(支持语言切换与内容加载)
文章目录 一、项目背景与功能概览二、项目技术架构与依赖安装2.1 技术栈2.2 安装依赖 三、国际化组件实现3.1 创建 i18n 实例3.2 配置 i18n 到 Vue 应用3.3 在组件中使用国际化内容3.4 支持语言切换 四、支持类型安全4.1 添加类型支持4.2 自动加载语言文件 一、项目背景与功能概…...

PhalApi 2.x:让PHP接口开发从“简单”到“极简”的开源框架
—— 专为高效开发而生,助你轻松构建高可用API接口 一、为什么选择PhalApi 2.x? 1.轻量高效,性能卓越 PhalApi 2.x 是一款专为接口开发设计的轻量级PHP框架,其核心代码精简但功能强大。根据开发者实测,在2核2G服务器…...

库magnet使用指南
Magnet 多线程控制库使用指南 目录 库功能概述环境配置核心类与接口基础使用示例代码生成工具高级功能与改进建议完整示例代码常见问题解答 https://blink.csdn.net/details/1872803?spm1001.2014.3001.5501 1. 库功能概述 Magnet 库提供以下核心功能: 多线程…...
 导出、导入补充>)
Oracle数据库数据编程SQL<9.3 数据库逻辑备份和迁移Data Pump (EXPDP/IMPDP) 导出、导入补充>
Oracle Data Pump 是 Oracle 10g 引入的高效数据迁移工具,相比传统的 EXP/IMP 工具,它提供了更强大的功能和显著的性能提升。以下是对 EXPDP 和 IMPDP 工具的全面讲解。 目录 一、高级功能扩展 1. 数据过滤与转换 2. 加密与安全 二、性能调优进阶 1. 并行处理优化 2. …...

Java 企业级应用:SOA 与微服务的对比与选择
企业级应用开发中,架构设计是决定系统可扩展性、可维护性和性能的关键因素。SOA(面向服务的架构)和微服务架构是两种主流的架构模式,它们各自有着独特的和设计理念适用场景。本文将深入探讨 SOA 和微服务架构的对比,并…...
)
Linux LED驱动(设备树)
Linux LED驱动(设备树) 之前的LED驱动直接在驱动文件中定义有关寄存器物理地址,然后使用io_remap函数进行内存映射,得到对应的虚拟地址,最后操作寄存器对应的虚拟地址完成对GPIO的初始化。 但也可以先在设备树文件中创…...

Zookeeper的典型应用场景?
大家好,我是锋哥。今天分享关于【Zookeeper的典型应用场景?】面试题。希望对大家有帮助; Zookeeper的典型应用场景? 1000道 互联网大厂Java工程师 精选面试题-Java资源分享网 ZooKeeper 是一个开源的分布式协调服务,主要用于管理和协调大…...

数据分析不只是跑个SQL!
数据分析不只是跑个SQL! 数据分析五大闭环,你做到哪一步了?闭环一:认识现状闭环二:原因分析闭环三:优化表现闭环四:预测走势闭环五:主动解读数据 数据思维:WHY-WHAT-HOW模…...
模型)
面试篇 - GPT-3(Generative Pre-trained Transformer 3)模型
GPT-3(Generative Pre-trained Transformer 3)模型 模型结构 与GPT-2一样,但是应用了Sparse attention: Dense attention:每个token之间两两计算attention,复杂度为O(n2)。 Sparse attention:…...

Dify智能体平台源码二次开发笔记(4) - 多租户的SAAS版实现
前言 Dify 的多租户功能是其商业版的标准功能,我们应当尊重其盈利模式。只有保持良性的商业运作,Dify 才能持续发展,并为用户提供更优质的功能。因此,此功能仅限学习使用。 我们的需求是:实现类似 SaaS 版的账号隔离&a…...

C# 13新特性 - .NET 9
转载: C# 13 中的新增功能 | Microsoft Learn C# 13 包括以下新增功能。 可以使用最新的 Visual Studio 2022 版本或 .NET 9 SDK 尝试这些功能:Introduced in Visual Studio 2022 Version 17.12 and newer when using C# 13 C# 13 中的新增功能 | Micr…...

【Code】《代码整洁之道》笔记-Chapter9-单元测试
第9章 单元测试 过去十年以来,编程专业领域进步很大。1997年时,没人听说过测试驱动开发。对于我们之中的大多数人来说,单元测试是那种用来确保程序“可运行”的用过即扔的短代码。我们辛勤地编写类和方法,再弄出一些特殊代码来测…...

java -jar 如何持久化运行
在 Linux 中,直接通过 java -jar 启动服务后关闭 SSH 客户端(如 Xshell)会导致服务终止,因为进程默认与当前终端会话绑定。以下是几种解决方案,确保服务在后台持久运行: (1)使用nohup命令,让进程忽略挂断信号,并在后台运行。 ps -ef | grep xxx.jar 或者 ps -ef …...
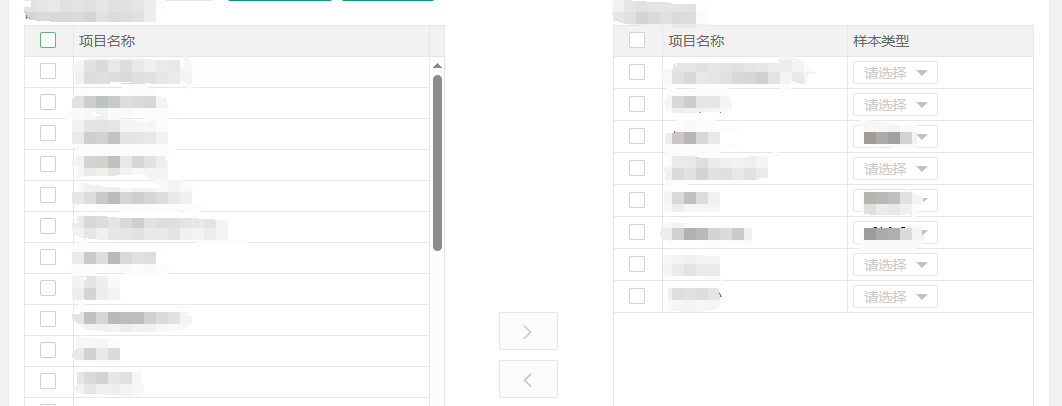
layui中transfer两个table展示不同的数据列
在项目的任务开发中需要达到transfer右侧table需要有下拉框可选择状态,左侧table不变 使用的layui版本为2.4.5,该版本没有对transfer可自定义数据列的配置,所以改动transfer.js中的源码 以下为transfer.js部分源码 也是transfer.js去render的…...

如何通过Radius认证服务器实现虚拟云桌面安全登录认证:安当ASP身份认证系统解决方案
引言:虚拟化时代的安全挑战 随着云计算和远程办公的普及,虚拟云桌面(如VMware Horizon、Citrix)已成为企业数字化办公的核心基础设施。然而,传统的用户名密码认证方式暴露了诸多安全隐患:弱密码易被暴力破…...

如何用DeepSeek大模型提升MySQL DBA工作效率?实战案例解析
如何用DeepSeek大模型提升MySQL DBA工作效率?实战案例解析 MySQL DBA(数据库管理员)的工作涉及数据库监控、SQL优化、故障排查、备份恢复等复杂任务,传统方式依赖手动操作和经验判断,效率较低。而DeepSeek大模型可以结…...

【机器学习】机器学习笔记
1 机器学习定义 计算机程序从经验E中学习,解决某一任务T,进行某一性能P,通过P测定在T上的表现因经验E而提高。 eg:跳棋程序 E: 程序自身下的上万盘棋局 T: 下跳棋 P: 与新对手下跳棋时赢的概率…...

CFD中的动量方程非守恒形式详解
在计算流体力学(CFD)中,动量方程可以写成守恒形式和非守恒形式,两者在数学上等价,但推导方式和应用场景不同。以下是对非守恒形式的详细解释: 1. 动量方程的守恒形式 首先回顾守恒形式的动量方程ÿ…...

如何在本地修改 Git 项目的远程仓库地址
✅ 场景说明 你当前的 Git 项目地址是: http://192.168.0.16/xxx.git你希望把它改成: http://192.168.0.22:8099/xxx.git🧩 操作步骤 步骤 ①:进入项目所在目录 你已经在正确路径下了: cd C:\Develop\xxx确认这个…...

clickhouse中的窗口函数
窗口函数 边界核心参数 窗口边界通过 ROWS、RANGE 或 GROUPS 模式定义,语法为: ROWS BETWEEN AND 基于 物理行位置 定义窗口,与排序键的实际值无关,适用于精确控制窗口行数 – 或 RANGE BETWEEN AND 基于 排序键的数值范围 定义窗口,适用于时间序列或连续数值的场景(…...

如何从项目目标到成功标准:构建可量化、可落地的项目评估体系
引言 在项目管理领域,"项目成功"的定义往往比表面看起来更复杂。根据PMI的行业报告,67%的项目失败源于目标与成功标准的不匹配。当项目团队仅关注"按时交付"或"预算达标"时,常会忽视真正的价值创造。本文将通…...

fbx/obj/glb/gltf/b3dm等通用格式批量转换成osgb
fbx/obj/glb/gltf/b3dm等通用格式批量转换成osgb fbx/obj/glb/gltf/b3dm等通用格式批量转换成osgb...
