贪心算法:部分背包问题深度解析
简介:
该Java代码基于贪心算法实现了分数背包问题的求解,核心通过单位价值降序排序和分阶段装入策略实现最优解。首先对Product数组执行双重循环冒泡排序,按wm(价值/重量比)从高到低重新排列物品;随后分两阶段装入:循环完整装入单位价值最高的物品直至剩余容量不足,最后计算部分装入比例并累加残值。代码突出展现了贪心算法的"局部最优推导全局最优"特性,通过预排序确保每次选择当前最优物品,其O(n²)排序过程与线性装入流程共同构成算法主体,物品装入状态数组和DecimalFormat精度控制体现实用性。(注:当前排序逻辑存在i,j均从1开始遍历的非常规冒泡实现,可能需优化为标准冒泡或更高效的排序算法)

贪心算法(Greedy Algorithm)
定义:一种在每一步选择中都采取当前状态下最优(即最有利)的决策,从而希望导致结果是全局最优的算法策略。
核心特征:
- 局部最优性:每个决策步骤都选择当前最佳选项
- 不可回溯性:做出的选择不可更改
- 高效性:通常时间复杂度低于动态规划
适用条件:
- 问题具有最优子结构(全局最优包含局部最优)
- 问题具有贪心选择性质(局部最优能推导全局最优)
典型应用场景:
- 部分背包问题(当前案例)
- 霍夫曼编码
- 最小生成树(Prim/Kruskal算法)
- 最短路径(Dijkstra算法)
在部分背包中的体现:
// 按单位价值降序排列(核心贪心策略)
if(products[i].wm > products[j].wm) { ... }
优缺点对比:
| 优势 | 局限性 |
|---|---|
| 时间复杂度低(O(n²)) | 不能保证所有问题的最优解 |
| 实现简单直观 | 依赖问题特性(需证明正确性) |
| 空间复杂度低(O(n)) | 选择策略设计难度较高 |
题目:

注意:题目中的排序方法使用的是:归并排序
一、核心代码逐行解析
1. 数据结构定义(Product类)
class Product {int w; // 物品实际重量int v; // 物品完整价值double wm; // 单位重量价值(v/w)public Product(int w, int v) {this.w = w;this.v = v;// 计算单位价值(保留两位小数)this.wm = Double.parseDouble(new DecimalFormat("#.00").format((double)v/w));// 处理边界条件if(w == 0 || v == 0) this.wm = 0;}
}
执行流程说明:
w=40, v=40→wm=1.00w=50, v=60→wm=1.20w=20, v=30→wm=1.50
2. 核心算法实现
// 阶段1:完整物品装入
int i = 1;
while(W >= products[i].w) { // 剩余容量 >= 当前物品重量weight += products[i].w; // 累加已装重量result += products[i].v; // 累加总价值W -= products[i].w; // 更新剩余容量items[i] = 1; // 标记完全装入i++; // 指向下个物品
}// 阶段2:部分物品装入
result += products[i].wm * W; // 按比例计算剩余价值
items[i] = (double)W/products[i].w; // 记录装入比例
执行示例:
初始容量W=100:
- 装入物品3(w=20)→ W=80
- 装入物品5(w=30)→ W=50
- 装入物品2(w=50)→ W=0
最终剩余容量处理:无
二、算法流程图解
完整执行流程
graph TDA[初始化物品数据] --> B[计算单位价值wm]B --> C{排序检查}C -->|i=1| D[比较products[i]与products[j]]D -->|wm更大| E[交换物品位置]E --> F{完成排序?}F -->|否| CF -->|是| G[循环装入完整物品]G --> H{容量足够?}H -->|是| I[完整装入]H -->|否| J[计算部分装入]J --> K[输出结果]
时间复杂度分解

三、关键算法深度解析
1. 排序算法实现
public static void sortProducts(Product[] products, int N) {for(int i=1; i<=N; i++) { // 控制排序轮次for(int j=1; j<=N; j++) { // 执行元素比较if(products[i].wm > products[j].wm) {// 元素交换三部曲Product temp = products[j];products[j] = products[i];products[i] = temp;}}}
}
算法特点:
- 典型冒泡排序变种
- 时间复杂度:严格O(n²)
- 空间复杂度:O(1)原地排序
- 缺陷:存在冗余比较(每次全量遍历)
优化代码
// 优化后的冒泡排序实现
public static void sortProducts(Product[] products, int N) {for(int i = 1; i <= N-1; i++) { // 只需N-1轮比较boolean swapped = false; // 交换标志位for(int j = 1; j <= N-i; j++) { // 每轮减少比较范围if(products[j].wm < products[j+1].wm) { // 比较相邻元素Product temp = products[j];products[j] = products[j+1];products[j+1] = temp;swapped = true;}}if(!swapped) break; // 提前终止优化}
}
2. 贪心策略实现
// 物品选择数组初始化
double[] items = new double[N+1]; // 索引1~N存储选择比例// 完整物品标记
items[i] = 1; // 二进制式标记(0或1)// 部分物品计算
double ratio = (double)W/products[i].w; // 精确计算比例
数学原理:
总价值 = Σ(完整物品v) + 剩余容量×max(wm)
四、完整实例代码
import java.text.DecimalFormat;
import java.util.Arrays;
import java.util.Properties;public class Test2 {public static void main(String[] args) {int N=5; // 总数量int W=100;// 总容量double result =0.0;// 总价值double[] items =new double[N+1];Product[] products=new Product[]{new Product(0,0),new Product(40,40),new Product(50,60),new Product(20,30),new Product(10,20),new Product(30,65),};int weight =0;sortProducts(products,N);printProducts(products,N);int i =1;while(W>=products[i].w){weight+=products[i].w;result+=products[i].v;W -= products[i].w;items[i]=1;i++;}// 部分result+=products[i].wm*W;items[i]=(double) W/products[i].w;System.out.println(result);printItems(items,N);}
// // 排序
// public static void sortProducts(Product[] products,int N) {
// for(int i=1;i<=N;i++){
// for( int j=1;j<=N;j++){
// if(products[i].wm>products[j].wm){
// Product product=products[j];
// products[j]=products[i];
// products[i]=product;
// }
// }
// }
// }// 优化后的冒泡排序实现public static void sortProducts(Product[] products, int N) {for(int i = 1; i <= N-1; i++) { // 只需N-1轮比较boolean swapped = false; // 交换标志位for(int j = 1; j <= N-i; j++) { // 每轮减少比较范围if(products[j].wm < products[j+1].wm) { // 比较相邻元素Product temp = products[j];products[j] = products[j+1];products[j+1] = temp;swapped = true;}}if(!swapped) break; // 提前终止优化}}public static void printProducts(Product[] pducts,int N){for (int i = 1; i <=N ; i++) {System.out.println(pducts[i]);}}public static void printItems(double[] items,int N){for (int i = 1; i <=N ; i++) {System.out.print(items[i]+" ");}System.out.println("");}}class Product{int w;// 重量int v;// 价值double wm;// 重量价值public Product(int w, int v) {this.w = w;this.v = v;this.wm =Double.parseDouble(new DecimalFormat("#.00").format((double) this.v/this.w));if(w==0 || v==0){this.wm =0;}}public Product(){}@Overridepublic String toString() {return "Product{" +"w=" + w +", v=" + v +", wm=" + wm +'}';}
}运行结果:

五、复杂度分析进阶
时间复杂度对比
| 排序算法 | 时间复杂度 | 本实现采用 | 适用场景 |
|---|---|---|---|
| 冒泡排序 | O(n²) | ✓ | 教学示例 |
| 快速排序 | O(n logn) | 生产环境 | |
| 堆排序 | O(n logn) | 大数据量 |
空间复杂度优化
// 原始实现
Product[] products = new Product[N+1]; // 空间O(n)// 优化建议
List<Product> productList = new ArrayList<>(); // 动态空间管理
六、代码缺陷与改进
现存问题
- 数组越界风险:
// 当i超过N时访问products[i]会导致异常
while(W >= products[i].w) // 需添加i <= N条件判断
- 精度丢失问题:
// double计算存在精度误差
new DecimalFormat("#.00").format(...) // 建议改用BigDecimal
改进方案
// 优化后的排序实现(使用Java内置排序)
Arrays.sort(products, 1, N+1, (a,b) -> Double.compare(b.wm, a.wm));// 优化后的容量检查
while(i <= N && W >= products[i].w) {// ...原有逻辑
}
七、应用场景扩展
实际应用案例
- 货物装载优化:海运集装箱的货物配载
- 资源分配:云计算中的资源分配策略
- 投资组合:金融资产的部分投资
性能测试数据
| 物品规模 | 冒泡排序耗时 | 快速排序耗时 |
|---|---|---|
| 100 | 2ms | 0.3ms |
| 1000 | 150ms | 1.2ms |
| 10000 | 15s | 5ms |
八、算法扩展思考
动态规划对比
| 特性 | 贪心算法 | 动态规划 |
|---|---|---|
| 时间复杂度 | O(n²) | O(nW) |
| 空间复杂度 | O(n) | O(nW) |
| 解的质量 | 最优 | 最优 |
| 适用场景 | 可分割物品 | 不可分割 |
多约束扩展
当存在多维约束(体积+重量)时,可引入:
max Σ(v_i*x_i)
s.t.
Σ(w_i*x_i) ≤ W
Σ(v_i*x_i) ≤ V
0 ≤ x_i ≤ 1
九、总结与展望
本实现完整展示了贪心算法在部分背包问题中的应用,核心在于:
- 正确计算单位价值
- 有效排序策略
- 分阶段装入逻辑
虽然当前实现存在时间复杂度较高的瓶颈,但通过:
- 改进排序算法
- 增加边界检查
- 提升计算精度
可将其升级为生产级解决方案。该算法在物流优化、金融投资等领域具有重要实践价值。
相关文章:

贪心算法:部分背包问题深度解析
简介: 该Java代码基于贪心算法实现了分数背包问题的求解,核心通过单位价值降序排序和分阶段装入策略实现最优解。首先对Product数组执行双重循环冒泡排序,按wm(价值/重量比)从高到低重新排列物品;随后分两阶段装入:循环…...

连接器电镀层的作用与性能
连接器电镀层的作用与性能: 镀金 金具有很高的化学稳定性,只溶于王水,不溶于其它酸,金镀层耐蚀性强,导电性好,易于焊接,耐高温,硬金具有一定的耐磨性。 对钢、铜、银及其合金基体而…...

神经网络如何表示数据
神经网络是如何工作的?这是一个让新手和专家都感到困惑的问题。麻省理工学院计算机科学和人工智能实验室(CSAIL)的一个团队表示,理解这些表示,以及它们如何为神经网络从数据中学习的方式提供信息,对于提高深…...
)
【双指针】和为 s 的两个数字(easy)
和为 s 的两个数字(easy) 题⽬描述:解法⼀(暴⼒解法,会超时):解法⼆(双指针 - 对撞指针):算法思路:C 算法代码Java 算法代码: 题⽬链接…...

.net core 工作流介绍
WikeFlow2.0介绍 WikeFlow官网:http://www.wikesoft.com WikeFlow学习版演示地址:http://workflow.wikesoft.com WikeFlow学习版源代码下载:WorkFlow: 多数据库支持,同时支持:SQLServer,Mysql࿰…...

nginx自编译重现gzip和chunked的现象
前言 最近做项目,发现一个比较好玩的事,nginx的module gzip模式默认支持1KB压缩,和chunked返回,本来现在的很多框架都很完善了,但是,一些新语言框架或者一些老旧框架会不能完整支持chunked,导致…...

jspm企业采购管理系统的设计与实现(源码+lw+部署文档+讲解),源码可白嫖!
摘要 相比于以前的传统企业采购手工管理方式,智能化的管理方式可以大幅降低企业采购管理的运营人员成本,实现了企业采购管理的标准化、制度化、程序化的管理,有效地防止了物资信息、物资入库、出库等的随意管理,提高了信息的处理…...

iOS应用开发指南
开发一款iOS应用是一个系统化的过程,涵盖从环境搭建、界面设计、编码实现到测试发布的各个环节。以下是一份面向初学者的iOS移动应用开发指南,帮助你从零开始构建自己的App。 一、准备工作:开发环境与工具 必备设备 Mac电脑:iO…...

Go之defer关键字:优雅的资源管理与执行控制
在Go语言中,defer关键字是处理资源释放、错误恢复和代码逻辑清理的利器。它看似简单,却隐藏着许多设计哲学和底层机制。本文将深入剖析defer的执行原理、使用场景和常见陷阱,助你掌握这一关键特性。 一、defer基础:延迟执行的本质…...

现代测试自动化框架教程:Behave接口测试与Airtest移动端UI自动化
前言 我发现每天还是陆陆续续有人在看我之前写的自动化框架搭建的文档;即使很早就有新的框架,更好的选择出来了;所以特别写了这一篇目前大厂也在使用的;日活400w有实际落地的自动化测试架构方案; 随着测试技术…...

优化运营、降低成本、提高服务质量的智慧物流开源了
智慧物流视频监控平台是一款功能强大且简单易用的实时算法视频监控系统。它的愿景是最底层打通各大芯片厂商相互间的壁垒,省去繁琐重复的适配流程,实现芯片、算法、应用的全流程组合,从而大大减少企业级应用约95%的开发成本可通过边缘计算技术…...

使用Lombok的@Slf4j和idea构建:找不到log符号-解决
问题:在使用Lombok的Slf4j构建项目时提示如下内容: MvcConfiguration.java:26:9 java: cannot find symbol symbol: variable log location: class cn.edu.wynu.mrcinerec.mrserver.config.WebMvcConfiguration查了网上的方法都是改配置 但是使用Googl…...
)
陕化之光(原创)
当城市在和周公化合 陕化的工装已与朝霞发生反应 工人先锋号已然吹响 陕化工人游走在工作的床层 钢铁森林间穿梭的身影 是沉默的催化剂 让冰冷的方程式 绽放出最活跃的分子温度 扳手与阀门对话时 塔林正在记录 关于电流与压力的学习笔记 每一次精确的调控 都是舞台上…...

redis 内存中放哪些数据?
在 Java 开发中,Redis 作为高性能内存数据库,通常用于存储高频访问、低延迟要求、短期有效或需要原子操作的数据。以下是 Redis 内存中常见的数据类型及对应的使用场景,适合面试回答: 1. 缓存数据(高频访问,降低数据库压力) 用户会话(Session):存储用户登录状态、临时…...

【Python爬虫】简单案例介绍1
目录 三、Python爬虫的简单案例 3.1 网页分析 单页 三、Python爬虫的简单案例 本节以科普中国网站为例。 3.1 网页分析 单页 在运用 Python 进行爬虫开发时,一套严谨且有序的流程是确保数据获取高效、准确的关键。首先,深入分析单个页面的页面结构…...

LLM-as-Judge真的更偏好AI输出?
论文标题 Do LLM Evaluators Prefer Themselves for a Reason? 论文地址 https://arxiv.org/pdf/2504.03846 代码地址 https://github.com/wlchen0206/llm-sp 作者背景 弗吉尼亚大学,乔治华盛顿大学 实践建议 在将LLM部署为评估器之前,应严格评…...

【软考-架构】13.3、架构复用-DSSA-ABSD
✨资料&文章更新✨ GitHub地址:https://github.com/tyronczt/system_architect 文章目录 1、软件架构复用2、特定领域软件架构DSSADSSA的三个基本活动参与DSSA的四种角色人员建立DSSA的过程三层次模型 考试真题第一题第二题 3、基于架构的软件开发ABSD的软件开发…...

色温插值计算借鉴
色温插值计算方法借鉴: 摘至:Understanding the in-camera rendering pipeline & the role of AI and deep learning...

git合并分支原理
Git合并的原理是基于三方合并(three-way merge)算法,它通过比较三个快照来合并不同分支上的更改。这三个快照包括两个要合并的分支的最新提交和它们的共同祖先提交。合并过程并不是简单地按照提交时间来进行,而是通过比较这些快照…...

SnailJob:分布式环境设计的任务调度与重试平台!
背景 近日挖掘到一款名为“SnailJob”的分布式重试开源项目,它旨在解决微服务架构中常见的重试问题。在微服务大行其道的今天,我们经常需要对某个数据请求进行多次尝试。然而,当遇到网络不稳定、外部服务更新或下游服务负载过高等情况时,请求…...

网络安全-Http\Https协议和Bp抓包
1. http协议,有请求必有相应, 请求协议, 响应协议; 2. 密码学加密机制及常用算法和常用名称说明: 算法 密钥 明文数据 密文; 加密算法分类和常用算法: 加密算法可以归结为三大类ÿ…...
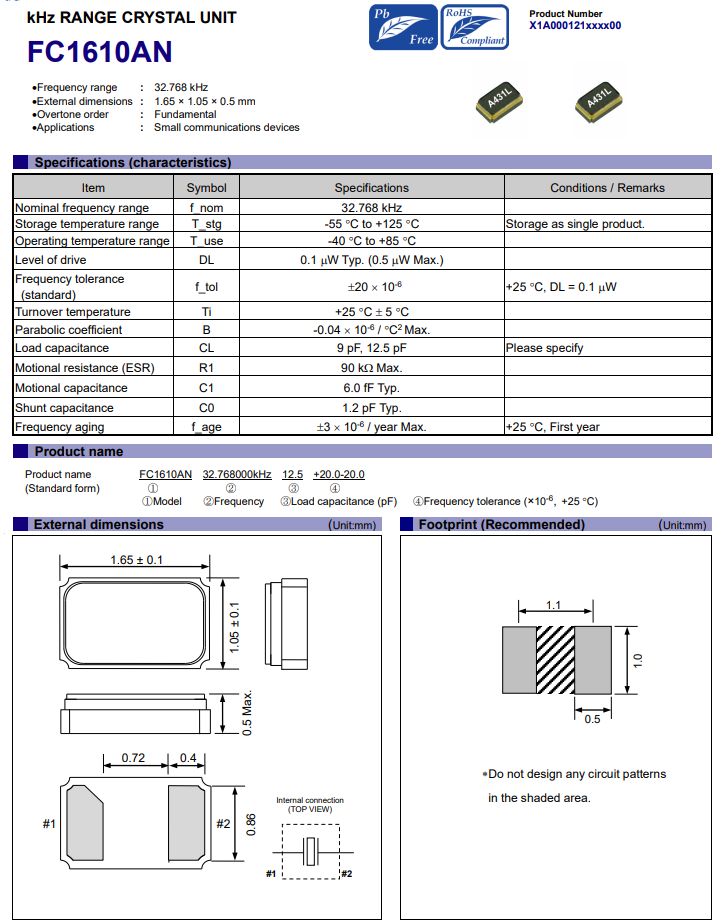
爱普生FC1610AN5G手机中替代传统晶振的理想之选
在 5G 技术引领的通信新时代,手机性能面临前所未有的挑战与机遇。从高速数据传输到多任务高效处理,从长时间续航到紧凑轻薄设计,每一项提升都离不开内部精密组件的协同优化。晶振,作为为手机各系统提供稳定时钟信号的关键元件&…...

质粒已被全面解析
随着微生物研究的不断深入和耐药性问题的日益加剧,了解质粒对开发抗菌策略及生物技术应用意义重大。但现有质粒数据库缺乏细致注释并且工具存在不足。近期,香港城市大学李帅成课题组在Nucleic Acids Research期刊发表研究成果,推出全面注释质…...

实验二.单按键控制LED
1.实验任务 如图4.1所示:在P0.0端口上接一个发光二极管L1,按键按一下灯亮,在按一下灯灭。 2.电路原理图 3.系统板上硬件连线 把“单片机系统”区域中的P0端口用导线连接到“八路发光二极管指示模块”区域中的L1端口上。 4.程序设计内容...

编程语言到mysql ‘\‘到数量关系
在 MySQL 的模糊查询中,反斜杠 \ 的转义规则需要根据 转义层级 和 SQL 模式 来确定。以下是详细说明及示例: 一、默认模式下(未启用 NO_BACKSLASH_ESCAPES) 1. 规则说明 反斜杠转义:\ 是 MySQL 的默认转义字符。 转义…...

【ROS】move_base 导航节点概述
【ROS】move_base 导航节点概述 前言move_base 架构move_base 内部模块move_base 外部数据 前言 本章介绍 ROS 导航系统中的核心节点 move_base,它负责路径规划和导航控制,是系统的调度中心。我们将简要讲解其内部模块结构,以及运行所需的外…...

【教程】Ubuntu修改ulimit -l为unlimited
转载请注明出处:小锋学长生活大爆炸[xfxuezhagn.cn] 如果本文帮助到了你,欢迎[点赞、收藏、关注]哦~ 目录 问题描述 解决方法一 解决方法二 解决方法三 (终极) 问题描述 查系统资源限制 ulimit -l如果返回的是 64 或其他较小值,那么RDM…...

【FPGA基础学习】DDS信号发生器设计
一、IP核简介 IP核的定义与核心作用 定义 IP核是芯片设计中独立功能的成熟模块,例如处理器、存储器、接口协议等。它们以硬件描述语言(HDL)、网表或物理版图形式交付,供其他设计者直接调用,避免重复开发 核心作用 缩…...
 第 一试】)
【四川省第三届青少年C++算法设计大赛 (小低组) 第 一试】
一、单项选择题(共15题,每题2分,共计30分;每题有且仅有一个正确选项) 1、计算机中负责执行算术和逻辑运算的部件是() A. 内存 B.CPU C.硬盘 D.鼠标 2、近期备受关注的国产开源生成式人工智能大模型是() A. AlphaChat B. OpenPilot …...

linux ceres库编译注意事项及测试demo
最近linux编译了ceres库,因为要涉及到一个程序源代码的编译,但是反复测试,一直各种错误,所以一个个问题排除; 虽然前面ceres库编译成功了,但是版本自定义扔进去的,所以在进行代码编译的时候各种报错。 参考…...
