排序（java）

一.概念

排序：对一组数据进行从小到大/从大到小的排序

稳定性：即使进行排序相对位置也不受影响如：

如果再排序后 L  在  i   的前面则稳定性差，像图中这样就是稳定性好。 

二.常见的排序

 三.常见算法的实现

1.插入排序

1.1 直接插入排序

时间复杂度

 最好情况：数据完全有序的时候O(N)

最坏的情况：数据完全逆序的时候O(N^2)

当前数据越有序越快

空间复杂度：O(1)

稳定性：稳定

 public static void insertSort(int[] array) {for (int i = 1; i < array.length; i++) {int tmp = array[i];int j = i - 1;for (; j >= 0; j--) {if (array[j] > tmp) {array[j + 1] = array[j];} else {break;}}array[j + 1] = tmp;}}

该排序就是从第二个数据开始进行比较，以第4个数据进行举例，假设第三个数据大于第四个数据则第一个数据的值就改为第三个数据，第二个数据不大于第四个数据循环结束，当前第二个数据后面的数据就是当时第四个数据的值。

1.2 希尔排序

public static void shellSort(int[] array) {int gap = array.length;while (gap > 1) {gap /= 2;shell(array, gap);}}private static void shell(int[] array, int gap) {for (int i = gap; i < array.length; i += gap) {int tmp = array[i];int j = i - gap;for (; j >= 0; j -= gap) {if (array[j] > tmp) {array[j + gap] = array[j];} else {break;}}array[j + gap] = tmp;}}

                                                                                                           c                      ,

 通过对数据分成多个组，随着组数越来越多，组的大小越来越小，数据也越归于有序，通常gap大小都是gap/=2，这种方法是对于插入算法的优化，但是因为gap不固定所以时间复杂度不固定。

稳定性：不稳定

2.选择排序

基本思想：每次都从元素中找一个最大/最小的值，放在初始/末尾位置。

2.1直接选择排序

方法一：

 public static void selectSort(int[] array) {for (int i = 0; i < array.length; i++) {int minIndex = i;for (int j = i + 1; j < array.length ; j++){if (array[j] < array[minIndex]) {minIndex = j;}}swap(array, minIndex, i);}
}

方法一就是找到一个最小的值放在初始位置。 

方法二：

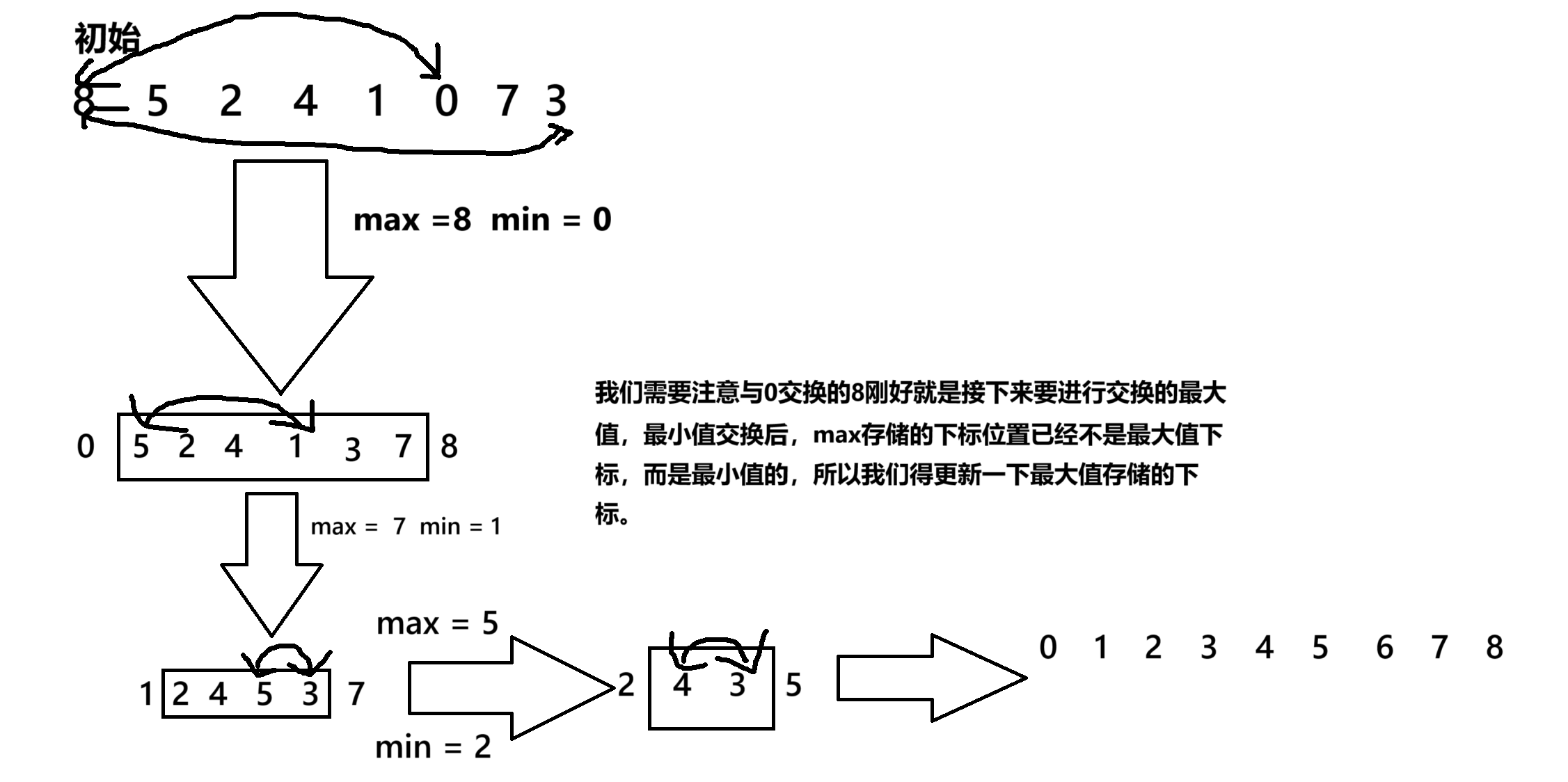
  public static void selsectSort2(int[] array){int left = 0;int right = array.length - 1;while (left < right){int minIndex = left;int maxIndex = left;for (int j = left + 1; j <= right; j++) {if (array[minIndex] > array[j]){minIndex = j;}if (array[maxIndex] < array[j]) {maxIndex = j;}}swap(array,left,minIndex);if(maxIndex == left){maxIndex =minIndex;}swap(array,right,maxIndex);left++;right--;}}

方法二就是找到最大值和最小值，然后进行交换，需要注意的是我们在进行最小值交换的时候。如果与最小值交换的元素刚好就是最大值，我们就需要进行判断一下。 然后将最大值的下标更新一下。

1.时间复杂度: O(N^2)

2.空间复杂度：O（1）

3.稳定性：不稳定

2.2堆排序

在使用堆时，我们已经知道可以根据创建一个大根堆来实现对于元素的排序，这种方法是因为大根堆的根结点是最大的，所以我们可以将它和最后一个交换位置，然后对排序元素个数减一后进行向下排序，此时可以确定的是最后一个元素是最大的。

 public static void heapSort(int[] array){creatBigHeap(array);int end = array.length - 1;while(end > 0){swap(array,0 ,end);end--;siftDown(0,array,end);}}public static void creatBigHeap(int[] arrray){for (int parent = (arrray.length - 1 - 1)/2; parent >= 0 ; parent--) {siftDown(parent, arrray,arrray.length);}}private static void siftDown(int parent,int[] array,int end) {int child = 2*parent + 1;while(child < end){if(child + 1 < end && array[child] < array[child+1]){child++;}if(array[child] > array[parent]){swap(array,child,parent);parent = child;child = parent*2 + 1;}else{break;}}}

时间复杂度：O（n*logN)

空间复杂度：O(1)

稳定性：不稳定的

3.交换排序

概念：通过比较大小来交换元素，元素大的向后走，元素小的向前走。

3.1冒泡排序

冒泡排序就是通过遍历来进行前后比较，来进行排序，通过这种方法，数组的末尾总是当前的最大值，所以我们在进行遍历比较是时，应该减去我们我们进行整体排序的次数，之所以给外循环的上限减去一，是因为我们在对n个数据进行在整体排序时，我们只需要排序n-1次就好，因为最后一个数据应该也是有序，没必要再进行排序。

时间复杂度：O(N^2)

空间复杂度： O(1)

稳定性：稳定

public static void popSort(int[] array){boolean flag = false;for (int i = 0; i < array.length - 1; i++) {for (int j = 0; j < array.length - 1 -i ; j++) {if (array[j] > array[j+1]) {swap(array, j, j + 1);flag = true;}}if (flag == false){break;}}}

3.2快速排序

基本思想就是取一个基准值，将当前数据分为大于基准值和小于基准值两个部分，然后再对这两个部分进行同样的操作，直到所有的元素都有序为止。

最好情况：O（N*logN)       满二叉树/完全二叉树

最坏情况：O（N^2)       单分支的树

空间复杂度：

最好情况：O(logN)       满二叉树/完全二叉树

最坏情况：O(N)            单分支的树

稳定性：不稳定              

3.2.1递归版

 private static void quick(int[] array,int start,int end) {if(start >= end){return;}int pivot = partition3(array,start,end);quick(array,start,pivot - 1);quick(array,pivot+1,end);}

3.2.1.1 Hoare版

  private static int parttionHoare(int[] array,int left,int right){int key = array[left];int i = left;while(left < right){while(left < right && array[right] >= key){right--;}while(left < right && array[left] <= key){left++;}swap(array,left,right);}swap(array,left,i);return left;}

Hoare版的快速排序就是从两边进行调整，左边一碰到大于基准的值就停下来，右边碰到小于基准的值就停下来，然后进行交换，就这样进行下去知道left >= right，最后我们left所停留的位置就是基准应该再的位置，但是基准开始被设为就是left，所以我们提前存的left就有了价值了，让他俩交换，就完成了一次快排。

3.2.1.2挖坑法

 private static int parttion2(int[] array,int left,int right){int key = array[left];while(left < right){while(left < right && array[right] >= key){right--;}array[left] = array[right];while(left < right && array[left] <= key){left++;}array[right] = array[left];}array[left] = key;return left;}

挖坑法就是先挖个坑让右边小于基准的值给填进去，这样右边就也有个坑了，然后再在左边找，找到一个大于基准的数，填满右边的坑，之后肯定有一个坑是空的，这就是我们要找的基准位置。 

3.2.1.3 双指针法

 private static int partition3(int[] array, int left, int right) {int prev = left;int pcur = left + 1;while(pcur <= right){if (array[left] > array[pcur] && array[++prev] != array[pcur]){swap(array,prev,pcur);}pcur++;}swap(array,left,prev);return prev;}

我们会以左边第一个元素为基准，如果碰到比基准小的值，我们会用用pcur来进行记录，而prev移动的条件就是当pcur遇到小的值时，而prev的下一个元素也必然时大于基准的，因为当前这个元素不大于基准pcur不能走。我们来画图举例：

3.2.2 非递归

public static void quickSortNor(int[] array){Stack<Integer> stack = new Stack<>();int left = 0;int right = array.length - 1;int pivot  = parttionHoare(array,left,right);if(pivot - 1 > left) {stack.push(left);stack.push(pivot - 1);}if(pivot + 1 < right) {stack.push(pivot+1);stack.push(right);}while(!stack.isEmpty()){right = stack.pop();left = stack.pop();pivot = parttionHoare(array,left,right);if(pivot - 1 > left){stack.push(left);stack.push(pivot - 1);}if(pivot + 1 < right){stack.push(pivot + 1);stack.push(right);}}}

非递归使用了栈，首先将元素分为大于基准和小于基准两组，然后重复进行操作，通过HOare操作来对数组进行排序。 

 快速排序优化

 private static void insertSortRange(int[] array,int begain,int end) {for (int i = begain + 1; i <= end; i++) {int tmp = array[i];int j = i - 1;for (; j >= begain; j--) {if (array[j] > tmp) {array[j + 1] = array[j];} else {break;}}array[j + 1] = tmp;}}private static void quick(int[] array,int start,int end) {if(start >= end){return;}if (end - start + 1 <= 15){//插入排序insertSortRange(array,start,end);return;}//三数取中int index =  midOfThree(array,start,end);swap(array,index,start);int pivot = parttionHoare(array,start,end);quick(array,start,pivot - 1);quick(array,pivot+1,end);}

当我们遇到小的区间可以用插入排序来解决，在选择基准时我们可以尽量选择取中间值来进行排序，所以我们又有了一个方法就是三数取中。

4.归并排序

基本思想：将一组数据分成两组，然后对分开的组在进行分组，直到分为一个组，然后进行合并，在合并过程中进行排序，开始时一 一排序，然后是二二，知道全部组都合并为一个组。

归并排序总结

1.归并排序缺点在于时间复杂度过高，因为占用外部空间来排序很多。 

2.时间复杂度：O(N*logN)

3.空间复杂度：O(N)

4.稳定性：稳定

代码实现

 public static void mergeSort(int[] array){mergeSortFunc(array,0,array.length - 1);}private static void mergeSortFunc(int[] array, int left, int right) {if(left >= right){return ;}int mid = (left + right) / 2;mergeSortFunc(array,left,mid);mergeSortFunc(array,mid + 1,right);merge(array,left,right,mid);}private static void merge(int[] array, int left, int right, int mid) {int s1 = left;int s2 = mid + 1;int[] tmpArr = new int[right - left + 1];int k = 0;while(s1 <= mid && s2 <= right){if (array[s2] <= array[s1]){tmpArr[k++] = array[s2++];}else{tmpArr[k++] = array[s1++];}}while (s1 <= mid){tmpArr[k++] = array[s1++];}while(s2 <= right){tmpArr[k++] = array[s2++];}for (int i = 0; i < tmpArr.length; i++) {array[i + left ] = tmpArr[i];}}

非递归实现

 public static void mergeSortNor(int[] array){int gap = 1;while(gap < array.length ){for (int i = 0; i < array.length; i += 2*gap ) {int left = i;int mid = left + gap - 1;int right = mid + gap;if (mid >= array.length){mid = array.length - 1;}if (right >= array.length){right = array.length - 1;}merge(array,left,right,mid);}gap*=2;}}

在这七大排序中稳定的只有归并排序，冒泡排序，插入排序，其中归并排序，快速排序，插入排序应当作为重点。

其他排序

计数排序

 public static void countSort(int[] array){int minVal = array[0];int maxVal = array[0];for (int i = 1; i < array.length; i++) {if (array[i] < minVal){minVal = array[i];}if (array[i] > maxVal){maxVal = array[i];}}int[] count = new int[maxVal - minVal + 1];for (int i = 0; i < array.length; i++) {count[array[i] - minVal]++;}int index = 0;for (int i = 0; i < count.length; i++) {while(count[i] > 0){array[index] = i+minVal;index++;count[i]--;}}}

通过对相同元素出现的次数来进行排序。