DAY09:【pytorch】nn网络层
1、卷积层
1.1 Convolution
1.1.1 卷积操作
- 卷积运算:卷积核在输入信号(图像)上滑动,相应位置上进行乘加
- 卷积核:又称为滤波器、过滤器,可认为是某种模式、某种特征
1.1.2 卷积维度
一般情况下,卷积核在几个维度上滑动就是几维卷积
- 一维卷积

- 二维卷积

- 三维卷积

1.2 nn.Conv2d

# nn.Conv2d(
# in_channels,
# out_channels,
# kernel_size,
# stride=1,
# padding=0,
# dilation=1,
# groups=1,
# bias=True,
# padding_mode='zeros'
# )
1.2.1 基本介绍
功能:对多个二维信号进行二维卷积
主要参数:
in_channels:输入通道数out_channels:输出通道数,等价于卷积核个数kernel_size:卷积核尺寸stride:步长padding:填充个数dilation:空洞卷积大小groups:分组卷积设置,默认为1,即不分组bias:是否使用偏置
尺寸计算:
H o u t = ⌊ H i n + 2 × p a d d i n g [ 0 ] − d i l a t i o n [ 0 ] × ( k e r n e l _ s i z e [ 0 ] − 1 ) − 1 s t r i d e [ 0 ] + 1 ⌋ H_{out} = \lfloor \frac{H_{in} + 2 \times padding[0] - dilation[0] \times (kernel\_size[0] - 1) - 1}{stride[0]} + 1 \rfloor Hout=⌊stride[0]Hin+2×padding[0]−dilation[0]×(kernel_size[0]−1)−1+1⌋
1.2.2 代码框架
conv_layer = nn.Conv2d(3, 1, 3) # input:(i, o, size) weights:(o, i , h, w)nn.init.xavier_normal_(conv_layer.weight.data)img_conv = conv_layer(img_tensor)
1.3 nn.ConvTranspose
# nn.ConvTranspose(
# in_channels,
# out_channels,
# kernel_size,
# stride=1,
# padding=0,
# output_padding=0,
# groups=1,
# bias=True,
# dilation=1,
# padding_mode='zeros'
# )
1.3.1 基本介绍
功能:用于对图像进行上采样
对比:
- 正常卷积:假设图像尺寸为4×4,卷积核为3×3,padding=0,stride=1,
则图像: I 16 ∗ 1 I_{16*1} I16∗1,卷积核: K 4 ∗ 16 K_{4*16} K4∗16,输出: O 4 ∗ 1 = K 4 ∗ 16 × I 16 ∗ 1 O_{4*1}=K_{4*16}×I_{16*1} O4∗1=K4∗16×I16∗1 - 转置卷积:假设图像尺寸为2×2,卷积核为3×3,padding=0,stride=1,
则图像: I 4 ∗ 1 I_{4*1} I4∗1,卷积核: K 16 ∗ 4 K_{16*4} K16∗4,输出: O 16 ∗ 1 = K 16 ∗ 4 × I 4 ∗ 1 O_{16*1}=K_{16*4}×I_{4*1} O16∗1=K16∗4×I4∗1
主要参数:
in_channels:输入通道数out_channels:输出通道数kernel_size:卷积核大小stride:步长padding:填充dilation:空洞卷积大小groups:分组卷积bias:是否使用偏置
尺寸计算: H o u t = ( H i n − 1 ) × s t r i d e [ 0 ] − 2 × p a d d i n g [ 0 ] + d i l a t i o n [ 0 ] × ( k e r n e l _ s i z e [ 0 ] − 1 ) + o u t p u t _ p a d d i n g [ 0 ] + 1 H_{out} = (H_{in} - 1) \times stride[0] - 2 \times padding[0] + dilation[0] \times (kernel\_size[0] - 1) + output\_padding[0] + 1 Hout=(Hin−1)×stride[0]−2×padding[0]+dilation[0]×(kernel_size[0]−1)+output_padding[0]+1
1.3.2 代码框架
conv_layer = nn.ConvTranspose2d(3, 1, 3, stride=2) # input:(i, o, size)nn.init.xavier_normal_(conv_layer.weight.data)img_conv = conv_layer(img_tensor)
2、池化层
2.1 概念

对信息进行收集并总结,类似水池收集水资源,因而得名池化层
- 收集:多变少
- 总结:最大值/平均值
2.2 nn.MaxPool2d
# nn.MaxPool2d(
# kernel_size,
# stride=None,
# padding=0,
# dilation=1,
# return_indices=False,
# ceil_mode=False,
# )
2.2.1 基本介绍
功能:对二维信号(图像)进行最大值池化
主要参数:
kernel_size:池化核大小stride:步长padding:填充dilation:池化核间隔大小return_indices:是否返回最大值索引ceil_mode:是否向上取整
2.2.2 代码框架
MaxPool2d
maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2)) # input:(i, o, size) weights:(o, i , h, w)img_pool = maxpool_layer(img_tensor)
MaxPool2dunpool
# poolingimg_tensor = torch.randint(high=5, size=(1, 1, 4, 4), dtype=torch.float)maxpool_layer = nn.MaxPool2d((2, 2), stride=(2, 2), return_indices=True)img_pool, indices = maxpool_layer(img_tensor)# unpoolingimg_reconstruct = torch.randn_like(img_pool, dtype=torch.float)maxunpool_layer = nn.MaxUnpool2d((2, 2), stride=(2, 2))img_unpool = maxunpool_layer(img_reconstruct, indices)
2.3 nn.AvgPool2d
# nn.AvgPool2d(
# kernel_size,
# stride=None,
# padding=0,
# ceil_mode=False,
# count_include_pad=True,
# divisor_override=None
# )
2.3.1 基本介绍
功能:对二维信号(图像)进行平均值池化
主要参数:
kernel_size:池化核大小stride:步长padding:填充ceil_mode:是否向上取整count_include_pad:是否包含填充的像素divisor_override:除数重写
2.3.2 代码框架
AvgPool2d
avgpoollayer = nn.AvgPool2d((2, 2), stride=(2, 2)) # input:(i, o, size) weights:(o, i , h, w)img_pool = avgpoollayer(img_tensor)
AvgPool2ddivisor_override
img_tensor = torch.ones((1, 1, 4, 4))avgpool_layer = nn.AvgPool2d((2, 2), stride=(2, 2), divisor_override=3)img_pool = avgpool_layer(img_tensor)
3、线性层
3.1 概念

又称全连接层,其每个神经元与上一层所有神经元相连实现对前一层的线性组合、线性变换
3.2 nn.Linear
# nn.Linear(
# in_features,
# out_features,
# bias=True
# )
3.2.1 基本介绍
功能:对一维信号(向量)进行线性组合
主要参数:
in_features:输入结点数out_features:输出结点数bias:是否使用偏置
计算公式: y = x W T + b i a s y = xW^T + bias y=xWT+bias
3.2.2 代码框架
inputs = torch.tensor([[1., 2, 3]])linear_layer = nn.Linear(3, 4)linear_layer.weight.data = torch.tensor([[1., 1., 1.],[2., 2., 2.],[3., 3., 3.],[4., 4., 4.]])linear_layer.bias.data.fill_(0.5)output = linear_layer(inputs)
4、激活函数层
4.1 nn.Sigmoid

计算公式: y = 1 1 + e − x y = \frac{1}{1 + e^{-x}} y=1+e−x1
梯度公式: y ‘ = y × ( 1 − y ) y^{`} = y \times (1 - y) y‘=y×(1−y)
特性:
- 输出值在(0, 1),符合概率
- 导数范围是[0, 0.25],易导致梯度消失
- 输出为非0,破坏数据分布
4.2 nn.tanh

计算公式: y = s i n x c o s x = e x − e − x e − + e − x = 2 1 + e − 2 x + 1 y = \frac{sinx}{cosx} = \frac{e^x - e^{-x}}{e^{-} + e^{-x}} = \frac{2}{1 + e^{-2x}} + 1 y=cosxsinx=e−+e−xex−e−x=1+e−2x2+1
梯度公式: y ‘ = 1 − y 2 y^{`} = 1 - y^2 y‘=1−y2
特性:
- 输出值在(-1, 1),数据符合0均值
- 导数范围是(0, 1),易导致梯度消失
4.3 nn.ReLU

计算公式: y = m a x ( 0 , x ) y = max(0, x) y=max(0,x)
梯度公式:
y ′ = { 1 , x > 0 undefined , x = 0 0 , x < 0 y' = \begin{cases} 1, & x > 0 \\ \text{undefined}, & x = 0 \\ 0, & x < 0 \end{cases} y′=⎩ ⎨ ⎧1,undefined,0,x>0x=0x<0
特性:
- 输出值均为正数,负半轴导致死神经元
- 导数是1,缓解梯度消失,但易引发梯度爆炸

4.3.1 nn.LeakuReLU
negative_slope: 负斜率的值,默认为0.01,即负斜率
4.3.2 nn.PReLU
init:可学习斜率
4.3.3 nn.RReLU
lower:均匀分布下限upper:均匀分布上限
微语录:黑暗中有人擎花而来,惊动火焰,燃烧万千蝴蝶迷了眼。
相关文章:

DAY09:【pytorch】nn网络层
1、卷积层 1.1 Convolution 1.1.1 卷积操作 卷积运算:卷积核在输入信号(图像)上滑动,相应位置上进行乘加卷积核:又称为滤波器、过滤器,可认为是某种模式、某种特征 1.1.2 卷积维度 一般情况下…...

大模型面试题
分布式训练相关面试题解答 什么是分布式训练? 分布式训练是一种利用多个计算节点(如多个 GPU 或多个机器)协同工作来加速训练机器学习模型的方法。它通过将训练任务分配给多个计算资源并行执行,以减少训练时间和处理大规模数据。…...

跟康师傅学Java-面向对象(基础)
跟康师傅学Java-面向对象(基础) 学习面向对象内容的三条主线(非官方) ①Java类及类的成员:(重点)属性、方法、构造器;(熟悉)代码块、内部类 ②面向对象的特征:封装、继承、多态、(抽象) ③其他关键字的使用:this、super、package、import、static、final、inte…...
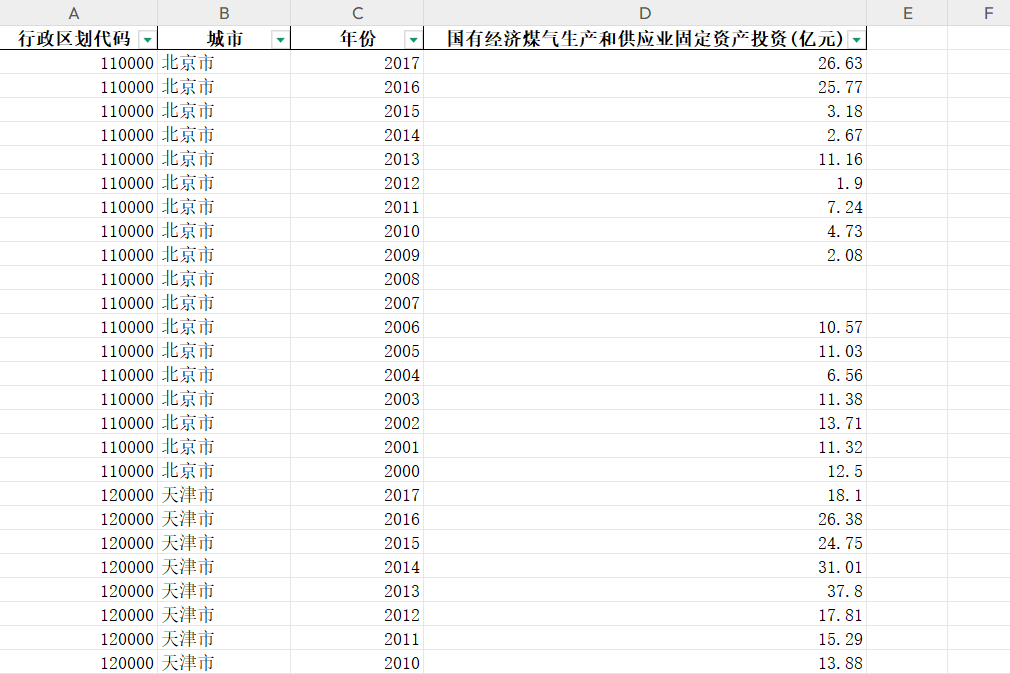
2000-2017年各省国有经济煤气生产和供应业固定资产投资数据
2000-2017年各省国有经济煤气生产和供应业固定资产投资数据 1、时间:2000-2017年 2、来源:国家统计局、能源年鉴 3、指标:行政区划代码、城市、年份、国有经济煤气生产和供应业固定资产投资 4、范围:31省 5、指标说明&#x…...

线性代数 | 知识点整理 Ref 3
注:本文为 “线性代数 | 知识点整理” 相关文章合辑。 因 csdn 篇幅合并超限分篇连载,本篇为 Ref 3。 略作重排,未整理去重。 图片清晰度限于引文原状。 如有内容异常,请看原文。 《线性代数》总复习要点、公式、重要结论与重点释…...

从原理到实践:NFS复杂故障处理方法论
#作者:孙德新 文章目录 一、nfs使用概述二、疑难故障现象描述三、原理分析四、解决方案五、优化服务器资源配置:六、故障案例总结七、故障预防建议八、nfs优化方法 一、nfs使用概述 NFS(Network File System)是一种分布式文件系…...

网络层IP协议知识大梳理
全是通俗易懂的讲解,如果你本节之前的知识都掌握清楚,那就速速来看我的IP协议笔记吧~ 自己写自己的八股!让未来的自己看懂! (全文手敲,受益良多) 网路基础3 网路层 TCP并没有把数据发到网路…...

【Web前端技术】第二节—HTML标签(上)
hello!好久不见—— 做出一个属于自己的网站! 云边有个稻草人-个人主页 Web前端技术—本篇文章所属专栏 目录 一、HTML 语法规范 1.1 基本语法概述 1.2 标签关系 二、HTML 基本结构标签 2.1 第一个 HTML 网页 2.2 基本结构标签总结 三、网页开发…...

1.Axum 与 Tokio:异步编程的完美结合
摘要 深入解析 Axum 核心架构与 Tokio 异步运行时的集成,掌握关键原理与实践技巧。 一、引言 在当今的软件开发领域,高并发和高性能是衡量一个系统优劣的重要指标。对于 Web 服务器而言,能够高效地处理大量并发请求是至关重要的。Rust 语言…...

08软件测试需求分析案例-删除用户
删除用户是后台管理菜单的一个功能模块,只有admin才有删除用户的权限。不可删除admin。 1.1 通读文档 通读需求规格说明书是提取信息,提出问题,输出具有逻辑、规则、流程的业务步骤。 信息:此功能应为用户提供确认删除的功能。…...

SDL基础
SDL SDL(Simple DirectMedia Layer)是一个开源的跨平台多媒体开发库,主要用于开发需要图形、音频和输入设备支持的应用程序。它使用C语言编写,提供了简单易用的API,**能够帮助开发者快速实现跨平台的多媒体功能。**SD…...
十三种通信接口芯片——《器件手册--通信接口芯片》
目录 通信接口芯片 简述 基本功能 常见类型 应用场景 详尽阐述 1 RS485/RS422芯片 1. RS485和RS422标准 2. 芯片功能 3. 典型芯片及特点 4. 应用场景 5. 设计注意事项 6. 选型建议 2 RS232芯片 1. RS232标准 2. 芯片功能 3. 典型芯片及特点 4. 应用场景 5. 设计注意事项 6…...
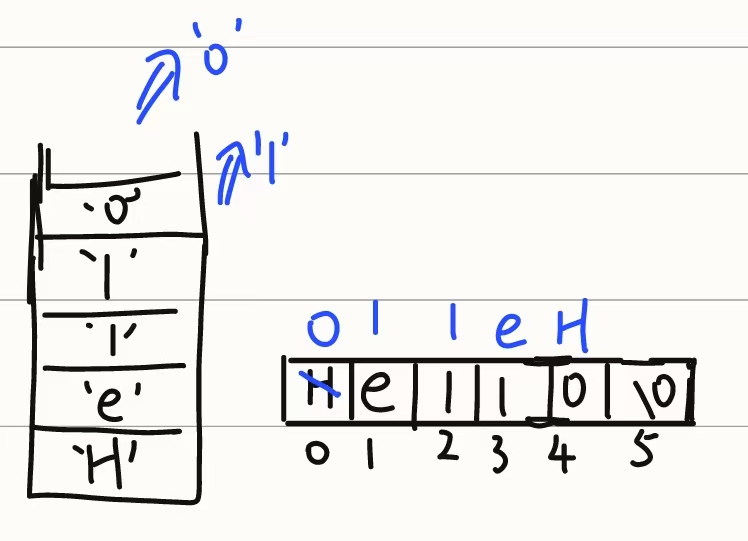
反转一个字符串
用数组栈实现 void Reverse(char *C, int len) {top -1;for(int i 0; i < len; i){push(C[i]);}for(int i 0; i < len; i){C[i] Top();pop();} } 全部函数 #include <stdio.h> #include <stdlib.h> #include <string.h>#define MAX_SIZE 101int …...

从GPT到Gemini 大模型进化史
从GPT到Gemini:大模型进化史 在过去的几年里,人工智能领域经历了翻天覆地的变化,其中最引人注目的莫过于大规模语言模型的发展。从最初的GPT系列到最近的Gemini,这些模型不仅在技术上取得了重大突破,还在实际应用中展…...

【限流算法】计数器、漏桶、令牌桶算法
1 计数器 使用计数器实现限流,可限制在指定时间间隔内请求数小于阈值的情况,但存在临界问题。如图1-17所示,假设每分钟系统限流500个请求,在XX:00:59时刻系统接收到500个请求,在XX:01:00时刻系统又接收到500个请求&am…...

秘密任务 2.0:如何利用 WebSockets + DTOs 设计实时操作
在之前的文章中,我们探讨了为什么 DTO 是提升 API 效率和安全性的秘密武器。现在,我们进入了一个全新的场景——我们将深入探讨如何通过 WebSockets DTOs 实现实时操作! Agent X 正在进行一项高风险的卧底任务。突然,总部更新了…...

RAII 技术详解
1. 核心概念 定义:RAII(Resource Acquisition Is Initialization,资源获取即初始化)是 C 中通过对象生命周期管理资源的核心机制,核心思想是将资源的获取与对象构造绑定、资源释放与对象析构绑定,确…...

Windows快速切换屏幕/桌面
windows自带的切屏 需要winctrl 小键盘左右键 但是! Windows使用还是键盘加鼠标舒服! 教程 安装autohotkey 代码 ~LWin & LButton::{SendInput "^#{Left}" ; 发送 Win Ctrl Left (切换到左侧虚拟桌面) } ; 使用花括号包裹命令&a…...

SpringAI+DeepSeek大模型应用开发——3 SpringAI简介
SpringAI整合了全球(主要是国外)的大多数大模型,而且对于大模型开发的三种技术架构都有比较好的封装和支持,开发起来非常方便; 不同的模型能够接收的输入类型、输出类型不一定相同。SpringAI根据模型的输入和输出类型…...

使用 Function 来编写策略模式:优雅而高效的设计模式实践
引言:为什么选择策略模式? 策略模式(Strategy Pattern)是行为设计模式中的经典之一,它允许我们定义一系列的算法或操作,并使得它们可以互换使用。策略模式的关键思想是将算法的实现与使用它们的上下文分离…...

Java字符串处理
Java字符串处理全解析:String、StringBuilder与StringBuffer 一、String类基础 1. String的本质 不可变对象:Java中的String对象一旦创建就不能修改底层实现:基于private final char value[]字符数组字符串池:JVM维护的特殊存储…...

JS实现RSA加密
目录 目标 环境 实现RSA加解密 计算RSA加密允许的最大字节长度 目标 使用JS实现RSA加密解密。计算RSA加密允许的最大字节长度。 环境 node-rsa 实现RSA加解密 const NodeRSA require(node-rsa);function getKey() {const keyLength512// 创建 RSA 密钥对const key new …...

MySQL GTID集合运算函数总结
MySQL GTID 有一些运算函数可以帮助我们在运维工作中提高运维效率。 1 GTID内置函数 MySQL 包含GTID_SUBSET、GTID_SUBTRACT、WAIT_FOR_EXECUTED_GTID_SET、WAIT_UNTIL_SQL_THREAD_AFTER_GTIDS 4个内置函数,用于GTID集合的基本运算。 1.1 GTID_SUBSET(set1,set2) …...

从“链主”到“全链”:供应链数字化转型的底层逻辑
1. 制造业与供应链数字化转型的必然性 1.1. 核心概念与战略重要性 制造业的数字化转型,是利用新一代数字技术(如工业互联网、人工智能、大数据、云计算、边缘计算等)对制造业的整体价值链进行根本性重塑的过程。这不仅涉及技术的应用&#…...
 -> impl Fn(y)` 的同学点进来!)
学习笔记十五——rust柯里化,看不懂 `fn add(x) -> impl Fn(y)` 的同学点进来!
🧠 Rust 柯里化从零讲透:看不懂 fn add(x) -> impl Fn(y) 的同学点进来! 🍔 一、什么是柯里化?先用一个超好懂的生活比喻 假设你在点一个汉堡: 你说:我要点一个鸡腿汉堡! 店员…...

定制化突围:遨游防爆手机的差异化竞争策略
在石油、化工、矿山等危险作业场景中,随着工业智能化与安全生产需求的升级,行业竞争逐渐从单一产品性能的比拼转向场景化解决方案的深度较量。遨游通讯以九重防爆标准为技术底座,融合多模稳控系统与全景前瞻架构,开辟出"千行…...

【Java学习笔记】进制与进制转换
进制与进制转换 一、进制介绍 二进制:0、1,满 2 进 1,以 0b 或 0B 开头。 十进制:0-9,满 10 进 1。 八进制:0-7,满 8 进 1,以数字 0 开头表示。 十六进制:0-9 及 A(10…...

士兵乱斗(贪心)
问题 B: 士兵乱斗 - USCOJ...

【C++面向对象】封装(下):探索C++运算符重载设计精髓
🔥个人主页 🔥 😈所属专栏😈 每文一诗 💪🏼 年年岁岁花相似,岁岁年年人不同 —— 唐/刘希夷《代悲白头翁》 译文:年年岁岁繁花依旧,岁岁年年看花之人却不相同 目录 C运…...

JVM初探——走进类加载机制|三大特性 | 打破双亲委派SPI机制详解
目录 JVM是什么? 类加载机制 Class装载到JVM的过程 装载(load)——查找和导入class文件 链接(link)——验证、准备、解析 验证(verify)——保证加载类的正确性 准备(Prepare&…...
