PyTorch - Tensor 学习笔记
上层链接:PyTorch 学习笔记-CSDN博客
Tensor
初始化Tensor
import torch
import numpy as np# 1、直接从数据创建张量。数据类型是自动推断的
data = [[1, 2],[3, 4]]
x_data = torch.tensor(data)torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
''' 输出:
tensor([[2, 1, 4, 3],[1, 2, 3, 4],[4, 3, 2, 1]])
'''# 2、从 NumPy 数组创建张量(反之亦然)
np_array = np.array(data)
x_np = torch.from_numpy(np_array)3、从另一个张量创建:
# 从另一个张量创建张量,新张量保留参数张量的属性(形状、数据类型),除非显式覆盖
x_ones = torch.ones_like(x_data) # retains the properties of x_data 保留原有属性
print(f"Ones Tensor: \n {x_ones} \n")x_rand = torch.rand_like(x_data, dtype=torch.float) # overrides the datatype of x_data 覆盖原有类型
print(f"Random Tensor: \n {x_rand} \n") 
4、使用随机值或常量值:(三个皆是数据类型默认为浮点型(torch.float32))
# 使用随机值或常量值创建张量:
shape = (2,3,) # shape是张量维度的元组,确定输出张量的维数
rand_tensor = torch.rand(shape) # 元素为 [0, 1) 中的随机浮点型,
ones_tensor = torch.ones(shape) # 元素为全 1
zeros_tensor = torch.zeros(shape) # 元素为全 0print(f"Random Tensor: \n {rand_tensor} \n")
print(f"Ones Tensor: \n {ones_tensor} \n")
print(f"Zeros Tensor: \n {zeros_tensor}")
torch.zeros((2, 3, 4))
''' 输出:
tensor([[[0., 0., 0., 0.],[0., 0., 0., 0.],[0., 0., 0., 0.]],[[0., 0., 0., 0.],[0., 0., 0., 0.],[0., 0., 0., 0.]]])
'''torch.ones((2, 3, 4))
''' 输出:
tensor([[[1., 1., 1., 1.],[1., 1., 1., 1.],[1., 1., 1., 1.]],[[1., 1., 1., 1.],[1., 1., 1., 1.],[1., 1., 1., 1.]]])
'''若想指定生成其他数据类型的张量,可以通过
dtype参数显式指定。例如:# 整数类型 rand_tensor_int = torch.rand((2, 3), dtype=torch.int32) print(rand_tensor_int.dtype) # 输出: torch.int32# 双精度浮点型 ones_tensor_double = torch.ones((2, 3), dtype=torch.float64) print(ones_tensor_double.dtype) # 输出: torch.float64
动手学深度学习的内容
x = torch.arange(12) # 创建行向量 x,其包含以0开始的前12个整数,默认创建为整数
# 除非额外指定,新的张量将存储在内存中,并采用基于CPU的计算。
# 输出:tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])x.shape # 访问张量(沿每个轴的长度)的形状
# 输出:torch.Size([12])x.numel() # 张量中元素的总数,即形状的所有元素乘积,可以检查它的大小(size)。因为这里在处理的是一个向量,所以它的shape与它的size相同
# 输出:12X = x.reshape(3, 4) # 改变张量的形状,而不改变其元素数量和元素值。
'''
把张量x从形状为(12,)的行向量转换为形状为(3,4)的矩阵。
这个新的张量包含与转换前相同的值,但是它被看成一个3行4列的矩阵。
重点说明:虽然张量的形状发生了改变,但其元素值并没有变。
注意,通过改变张量的形状,张量的大小不会改变。
输出:
tensor([[ 0, 1, 2, 3],[ 4, 5, 6, 7],[ 8, 9, 10, 11]])
'''属性
Tensor 属性描述其形状、数据类型和存储它们的设备
tensor = torch.rand(3,4)
print(f"Shape of tensor: {tensor.shape}") # 形状
print(f"Datatype of tensor: {tensor.dtype}") # 数据类型
print(f"Device tensor is stored on: {tensor.device}") # 存储其的设备
操作(形状相同的两个矩阵)
索引和切片:(类似 numpy )
tensor = torch.ones(4, 4)
# tensor = torch.tensor([[1, 2, 3, 4],
# [5, 6, 7, 8],
# [9, 10, 11, 12],
# [13, 14, 15, 16]])print(f"First row: {tensor[0]}")
print(f"First column: {tensor[:, 0]}")
print(f"Last column: {tensor[..., -1]}")
tensor[:,1] = 0
print(tensor)

与任何Python数组一样:第一个元素的索引是0,最后一个元素索引是-1; 可以指定范围以包含第一个元素和最后一个之前的元素,即。
x = torch.arange(12) # 创建行向量 x,其包含以0开始的前12个整数,默认创建为整数
# 除非额外指定,新的张量将存储在内存中,并采用基于CPU的计算。
# 输出:tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])X = x.reshape(3, 4) # 改变张量的形状,而不改变其元素数量和元素值。
'''
把张量x从形状为(12,)的行向量转换为形状为(3,4)的矩阵。
这个新的张量包含与转换前相同的值,但是它被看成一个3行4列的矩阵。
重点说明:虽然张量的形状发生了改变,但其元素值并没有变。
注意,通过改变张量的形状,张量的大小不会改变。
输出:
tensor([[ 0, 1, 2, 3],[ 4, 5, 6, 7],[ 8, 9, 10, 11]])
'''X[-1], X[1:3] # [-1]选择最后一个元素,[1:3]选择第二个和第三个元素
'''
(tensor([ 8., 9., 10., 11.]),tensor([[ 4., 5., 6., 7.],[ 8., 9., 10., 11.]]))
'''X[1, 2] = 9 # 指定索引第二行第三列,将元素9写入矩阵
'''
array([[ 0., 1., 2., 3.],[ 4., 5., 9., 7.],[ 8., 9., 10., 11.]])
'''# 多个元素赋值相同的值
X[0:2, :] = 12 # [0:2, :]访问第1行和第2行,其中“:”代表沿轴1(列)的所有元素
'''
array([[12., 12., 12., 12.],[12., 12., 12., 12.],[ 8., 9., 10., 11.]])
'''torch.cat() 拼接张量 (沿给定维度连接一系列张量)。
另请参见 torch.stack, 另一个与 . 略有不同的 Tensor Joining 运算符。torch.cattorch.cat
'''
dim=1 :沿着第 1 维(通常是列)进行拼接
如果 tensor 的形状是 (a, b),
则沿着第 1 维拼接三次后,结果张量 t1 的形状将是 (a, b * 3)。
'''
t1 = torch.cat([tensor, tensor, tensor], dim=1) # 沿着第 1 维拼接三次
print(t1)

- 沿行连结(轴-0,形状的第一个元素)
- 按列连结(轴-1,形状的第二个元素)
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
torch.cat((X, Y), dim=0), torch.cat((X, Y), dim=1)
''' 输出:
(tensor([[ 0., 1., 2., 3.],[ 4., 5., 6., 7.],[ 8., 9., 10., 11.],[ 2., 1., 4., 3.],[ 1., 2., 3., 4.],[ 4., 3., 2., 1.]]),tensor([[ 0., 1., 2., 3., 2., 1., 4., 3.],[ 4., 5., 6., 7., 1., 2., 3., 4.],[ 8., 9., 10., 11., 4., 3., 2., 1.]]))
'''单个张量 (tensor.sum()求和 & 转int/float)
.sum() 聚合所有 值转换为一个值;.item() 将其转换为 Python 数值使用。
agg = tensor.sum() # 所有元素求和,返回新的张量(标量张量)
agg_item = agg.item() # 将标量张量agg转成Python的基本数据类型(如 float或int,具体取决于张量中数据的类型)
print(agg_item, type(agg_item))# 输出 agg的值为 tensor(12.)![]()
a = torch.tensor([3.5])
a, a.item(), float(a), int(a)
# (tensor([3.5000]), 3.5, 3.5, 3)算术运算
矩阵乘法 和 元素积(逐元素乘积)
计算两张量间的 矩阵乘法 和 元素积(逐元素乘积)
# 计算两个张量间的矩阵乘法
# This computes the matrix multiplication between two tensors. y1, y2, y3 will have the same value
# ``tensor.T`` 返回张量的转置 returns the transpose of a tensor
y1 = tensor @ tensor.T # “@”是矩阵乘法的简写,用于张量之间的矩阵乘法; tensor.T 返回 tensor 的转置
y2 = tensor.matmul(tensor.T) # matmul用于矩阵乘法,与 @ 功能等价y3 = torch.rand_like(y1) # 创建与 y1 形状相同的新张量,元素为随机值
torch.matmul(tensor, tensor.T, out=y3) # 进行矩阵乘法,并将结果存储在 y3 中print("Matrix Multiplication Results:") # y1, y2, y3 三者相等
print("y1:\n", y1)
print("y2:\n", y2)
print("y3:\n", y3)# 计算元素积
# This computes the element-wise product. z1, z2, z3 will have the same value
z1 = tensor * tensor # 对 tensor 进行逐元素相乘
z2 = tensor.mul(tensor) # 与 * 相同的逐元素相乘z3 = torch.rand_like(tensor)
torch.mul(tensor, tensor, out=z3) # 使用 torch.mul 函数对 tensor 进行逐元素相乘,并将结果存储在 z3 中print("\nElement-wise Product Results:") # z1, z2, z3 三者相等
print("z1:\n", z1)
print("z2:\n", z2)
print("z3:\n", z3)

按元素操作 (加减乘除 **幂 等)
对于任意具有相同形状的张量, 常见的标准算术运算符(+、-、*、/和**)都可以被升级为按元素运算。 我们可以在同一形状的任意两个张量上调用按元素操作。
在下面的例子中,使用逗号来表示一个具有5个元素的元组,其中每个元素都是按元素操作的结果。
x = torch.tensor([1.0, 2, 4, 8])
y = torch.tensor([2, 2, 2, 2])
x + y, x - y, x * y, x / y, x ** y # **运算符是求幂运算
''' 输出:
(tensor([ 3., 4., 6., 10.]),tensor([-1., 0., 2., 6.]),tensor([ 2., 4., 8., 16.]),tensor([0.5000, 1.0000, 2.0000, 4.0000]),tensor([ 1., 4., 16., 64.]))
'''逻辑运算符构建二元张量
以X == Y为例: 对于每个位置,如果X和Y在该位置相等,则新张量中相应项的值为1。 这意味着逻辑语句X == Y在该位置处为真,否则该位置为0。
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
X == Y
''' 输出:
tensor([[False, True, False, True],[False, False, False, False],[False, False, False, False]])
'''torch.exp() 对张量中每个元素计算自然指数
“按元素”方式可以应用更多的计算,包括像求幂这样的一元运算符:
用于对张量中每个元素计算自然指数函数 的函数,常用于 实现 softmax、log-normalization、指数增长建模 等场景:
对输入张量中的每个元素 执行:
其中
import torch
x = torch.tensor([1.0, 2, 4, 8])
torch.exp(x)
''' 输出:
tensor([2.7183e+00, 7.3891e+00, 5.4598e+01, 2.9810e+03])
'''x = torch.tensor([0.0, 1.0, 2.0])
y = torch.exp(x)
print(y) # 输出:tensor([1.0000, 2.7183, 7.3891])x = torch.tensor([[0.0, -1.0], [1.0, -2.0]])
print(torch.exp(x))
''' 输出:
tensor([[1.0000, 0.3679],[2.7183, 0.1353]])
'''常见应用:Softmax 的实现
x = torch.tensor([1.0, 2.0, 3.0]) softmax = torch.exp(x) / torch.sum(torch.exp(x)) print(softmax)常见应用:概率建模中的对数概率反变换
log_probs = torch.tensor([-1.0, -2.0]) probs = torch.exp(log_probs)常见应用:正态化、注意力机制等。
注意:
- 输入为负数时,输出仍为正数(因为
对任意实数
成立)。
- 大数值可能导致数值溢出(输出为
inf),因此常配合数值稳定性处理(如在 softmax 前减去最大值)使用。
使用NumPy桥接
- 共享内存:Tensor 和 NumPy 数组在
.numpy()和torch.from_numpy()转换时,会 共享底层内存(共享底层数据存储),因此对一方的修改会直接影响另一方。 - 潜在风险:如果对共享内存的张量或数组进行了非原地安全的操作(如直接赋值),可能导致数据竞争或意外覆盖。
以下例子中 t 和 n 的值始终同步,因为它们共享相同的内存。这种特性在需要高效数据传递时非常有用,但需要谨慎操作以避免数据竞争。
Tensor 转 NumPy 数组
t = torch.ones(5) # 创建一个包含 5 个 1.0 的张量
print(f"t: {t}")# 将张量 t 转换为 NumPy 数组
n = t.numpy() # .numpy() 方法将 PyTorch 张量转换为 NumPy 数组
print(f"n: {n}")![]()
张量的变化反映在 NumPy 数组中:
t.add_(1) # 使用 add_ 进行原地加法
print(f"t: {t}")
print(f"n: {n}") # n 的值也会改变,因为 t 和 n 共享内存![]()
NumPy 数组 转 Tensor
n = np.ones(5) # 创建一个包含 5 个 1.0 的 NumPy 数组
t = torch.from_numpy(n) # 将 NumPy 数组转换为 PyTorch 张量NumPy 数组中的更改反映在张量中:
np.add(n, 5, out=n) # 对 NumPy 数组,使用 out 参数 进行原地加法操作
print(f"t: {t}") # 由于 t 和 n 底层共享内存,t 的值也会随之改变
print(f"n: {n}")
x = torch.arange(12) # 创建行向量 x,其包含以0开始的前12个整数,默认创建为整数
# 除非额外指定,新的张量将存储在内存中,并采用基于CPU的计算。
# 输出:tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])X = x.reshape(3, 4) # 改变张量的形状,而不改变其元素数量和元素值。
'''
把张量x从形状为(12,)的行向量转换为形状为(3,4)的矩阵。
这个新的张量包含与转换前相同的值,但是它被看成一个3行4列的矩阵。
重点说明:虽然张量的形状发生了改变,但其元素值并没有变。
注意,通过改变张量的形状,张量的大小不会改变。
输出:
tensor([[ 0, 1, 2, 3],[ 4, 5, 6, 7],[ 8, 9, 10, 11]])
'''A = X.numpy()
B = torch.tensor(A)
type(A), type(B) # 输出:(numpy.ndarray, torch.Tensor)广播机制(形状不同的两个矩阵)
在上面的部分中,我们看到了如何在相同形状的两个张量上执行按元素操作。 在某些情况下,即使形状不同,我们仍然可以通过调用 广播机制(broadcasting mechanism)来执行按元素操作。 这种机制的工作方式如下:
-
通过适当复制元素来扩展一个或两个数组,以便在转换之后,两个张量具有相同的形状;
-
对生成的数组执行按元素操作。
在大多数情况下,我们将沿着数组中长度为1的轴进行广播,如下例子:
a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
a, b
''' 输出
(tensor([[0],[1],[2]]),tensor([[0, 1]]))
'''由于a和b分别是形状不同的 3*3 和 1*2 矩阵,若让它们相加,它们的形状不匹配。 我们将两个矩阵广播为一个更大的3*2 矩阵,如下所示:
# 矩阵a将复制列, 矩阵b将复制行,然后再按元素相加。
a + b
''' 输出
tensor([[0, 1],[1, 2],[2, 3]])
'''节省内存
运行一些操作可能会导致为新结果分配内存。
例如,执行 Y = X + Y,我们将取消引用Y指向的张量,而是指向新分配的内存处的张量。
id() 返回内存中引用对象的确切地址
before = id(Y)
Y = Y + X
id(Y) == before # 输出:False如上,运行Y = Y + X后,id(Y) 指向了另一个位置。 这是因为Python首先计算Y + X,为结果分配新的内存,然后使Y指向内存中的这个新位置。
这可能是不可取的,原因有两个:
-
在机器学习中,可能会有数百兆的参数,且在一秒内多次更新所有参数。因此,为避免不必要地分配内存,我们希望原地执行这些参数更新;
-
若不原地更新,其他引用仍然会指向旧的内存位置,这样某些代码可能会无意中引用旧的参数。
执行原地操作 (避免不必要地分配内存)
使用切片表示法将操作的结果分配给先前分配的数组,例如Y[:] = <expression>。
Z = torch.zeros_like(Y) # 创建 形状与Y相同的新矩阵Z,zeros_like将元素设全0
print('id(Z):', id(Z))
Z[:] = X + Y
print('id(Z):', id(Z))
'''
id(Z): 140327634811696
id(Z): 140327634811696
'''若后续计算中没有重复使用X,也可以使用 X[:]=X+Y 或 X+=Y 来减少操作的内存开销:
before = id(X)
X += Y
id(X) == before # 输出:TrueIn-place 操作
add_是一个 in-place 操作,会直接修改原张量tensor的值,而不会创建新的张量。- 若不想修改原张量,可使用非 in-place 操作
tensor + 5,这样会返回一个新的张量,而原张量保持不变。
# 使用 in-place 操作对张量中的每个元素加 5
print(f"{tensor} \n")
tensor.add_(5) # add_ 是 in-place 操作,会直接修改原张量
print(tensor)
in-place 的优缺点
优点:节省内存。(直接在原张量上操作,避免额外分配内存)
缺点:因为是直接修改原数据,会丢失历史记录,因此不鼓励使用。
相关文章:

PyTorch - Tensor 学习笔记
上层链接:PyTorch 学习笔记-CSDN博客 Tensor 初始化Tensor import torch import numpy as np# 1、直接从数据创建张量。数据类型是自动推断的 data [[1, 2],[3, 4]] x_data torch.tensor(data)torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])输出&am…...

Navicat、DataGrip、DBeaver在渲染 BOOLEAN 类型字段时的一种特殊“视觉风格”
文章目录 前言✅ 为什么 Boolean 字段显示为 [ ]?✅ 如何验证实际数据类型?✅ 小结 前言 看到的 deleted: [ ] 并不是 Prisma 的问题,而是数据库客户端(如 Navicat、DataGrip、DBeaver)在渲染 BOOLEAN 类型字段时的一种…...

基于 Vue3 + ECharts + GeoJson 实现区域地图钻取功能详解
文章目录 前言一、实现步骤1. 项目初始化2. 准备GeoJson数据3. 创建地图组件4. 创建主页面组件5. 使用组件 二、功能亮点三、性能优化建议四、常见问题解决五、结语六、实战demo七、资源下载 前言 在数据可视化领域,地图展示是一种非常直观的表现形式。而地图钻取&…...

安卓学习24 -- 网络
1 整体架构 (出处见水印) 这两张是能找到的比较清楚的图。目前可以看出,底层的网络业务,还是传统的linux内核提供。(注:这两个图我个人觉得不是非常对。。。) 在安卓上增加的两个比较重要的部…...

github新建一个远程仓库并添加了README.md,本地git仓库无法push
1.本地git仓库与远程仓库绑定 2.push时报错,本地的 main 分支落后于远程仓库的 main 分支(即远程有更新,但你本地没有),需要拉取远程的仓库--->在merge合并(解决冲突)--->push 3.但是git …...

Python:使用web框架Flask搭建网站
Date: 2025.04.19 20:30:43 author: lijianzhan Flask 是一个轻量级的 Python Web 开发框架,以简洁灵活著称,适合快速构建中小型 Web 应用或 API 服务。以下是 Flask 的核心概念、使用方法和实践指南 Flask 的核心特点: 轻量级 核心代码仅约…...

FTP协议命令和响应码
文章目录 📦 一、什么是 FTP 协议?🧾 二、FTP 常见命令(客户端发送)📡 三、FTP 响应码(服务端返回)📌 响应码分类(第一位)✅ 常见成功响应码&…...

*数字信号基础
数字信号基础:从采样到处理的完整解析 数字信号是离散时间、离散幅度的信号,与连续时间的模拟信号相对。它在现代通信、音频处理、图像识别等领域有广泛应用。以下是数字信号的核心概念、处理流程及关键技术。 1. 数字信号 vs. 模拟信号 特性模拟信号数…...
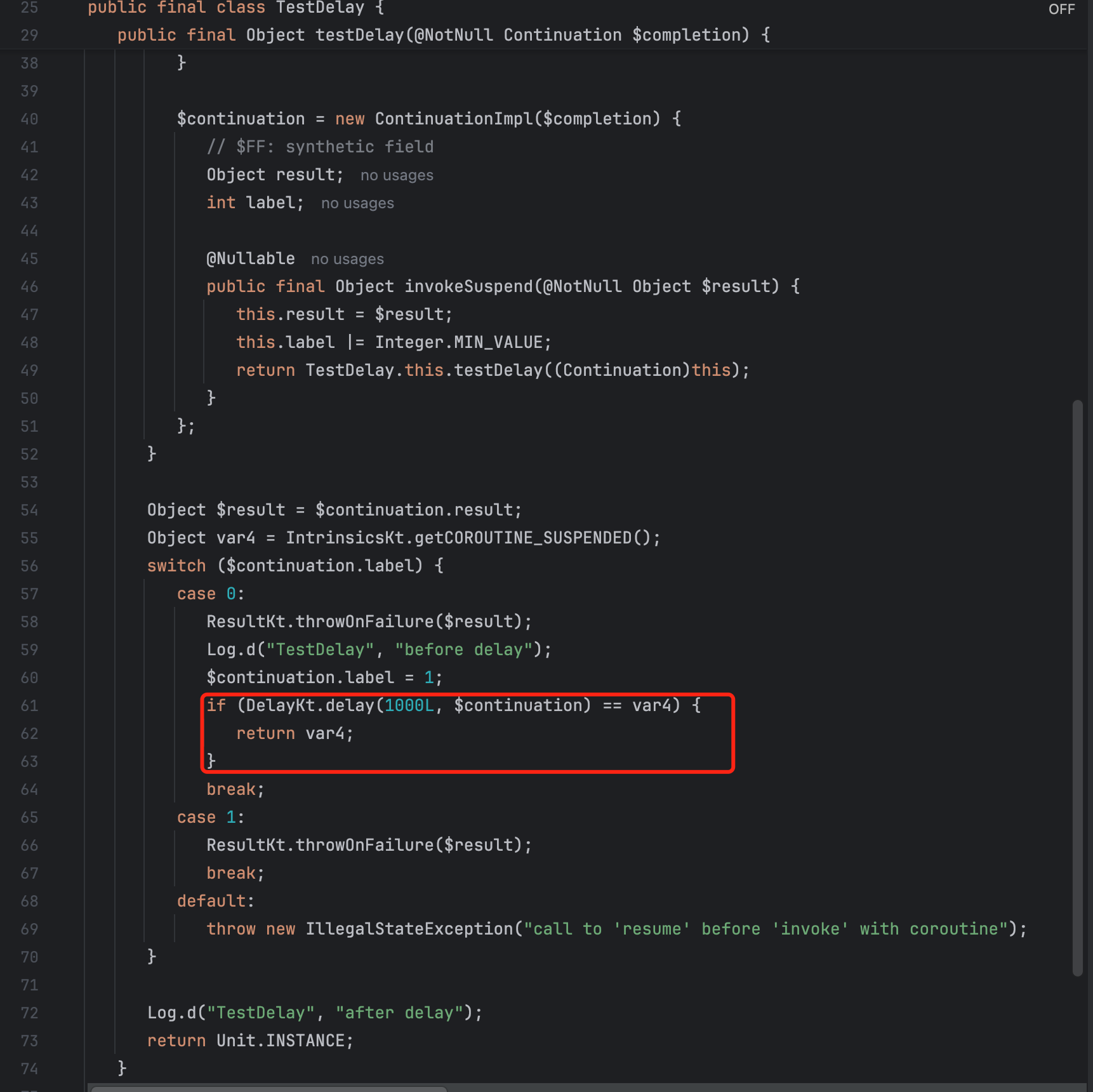
Kotlin delay方法解析
本文记录了kotlin协程(Android)中delay方法的字节码实现,并解析了delay方法如何实现挂起操作。 一、delay方法介绍 1.1、delay方法使用举例 class TestDelay {suspend fun testDelay() {Log.d("TestDelay", "before delay")delay(1000)Log.d…...

PHP框架在大规模分布式系统中的适用性如何?
随着互联网业务的指数级增长,大规模分布式系统已成为支撑高并发、高可用服务的核心技术架构,同时也成为众多互联网企业的首选架构。本文将带大家全面剖析PHP框架在分布式系统中的适用性,并结合实战案例帮大家提供技术选型建议。 一、PHP框架…...

【Vulkan 入门系列】创建描述符集布局和图形管线(五)
描述符集布局定义了着色器如何访问资源(如缓冲区和图像),是渲染管线配置的关键部分。图形管线定义了从顶点数据到最终像素输出的整个处理流程,包括可编程阶段(如顶点和片段着色器)和固定功能阶段࿰…...

Web前端:百度首页克隆 - 前端开发练习
一、项目概述 1.1 练习目标:通过实现百度首页经典布局掌握HTMLCSS基础布局能力 1.2 功能要求: 顶部导航栏布局中央搜索区布局底部信息栏布局基础交互效果 二、技术栈 HTML5 语义化标签CSS3 样式传统布局方案(浮动布局)基础CSS…...

mysql中in的用法详解
MySQL 中 IN 操作符用法详解 IN 是 MySQL 中用于多值筛选的高效操作符,常用于 WHERE 子句,可替代多个 OR 条件,简化查询逻辑并提升可读性。以下从基础语法、应用场景、性能优化、常见问题及高级技巧进行全方位解析。 一、基础语法与优势 1.…...

MySQL为什么默认使用RR隔离级别?
大家好,我是锋哥。今天分享关于【MySQL为什么默认使用RR隔离级别?】面试题。希望对大家有帮助; MySQL为什么默认使用RR隔离级别? 1000道 互联网大厂Java工程师 精选面试题-Java资源分享网 MySQL 默认使用 RR(Repeatable Read)…...

施磊老师基于muduo网络库的集群聊天服务器(二)
文章目录 Cmake简单介绍Cmake与MakefileCmake配置CmakeLists.txt 编写完整cmake例子文件夹杂乱问题多级目录Cmakevscode 极其推荐 的 cmake方式 Mysql环境与编程mysql简单使用User表Friend表AllGroup表GroupUser表OfflineMessage表 集群聊天项目工程目录创建网络模块代码Chatse…...

Git拉分支技巧:从零开始创建并推送分支
Git拉分支技巧:从零开始创建并推送分支 在团队协作开发中,Git 分支管理是不可或缺的技能。合理地创建、同步和推送分支,不仅能提高开发效率,还能避免代码冲突。本文将基于以下技巧,详细讲解如何从零开始创建并推送一个…...

Kotlin实现Android应用保活方案
Kotlin实现Android应用保活优化方案 以下的Android应用保活实现方案,更加符合现代Android开发规范,同时平衡系统限制和用户体验。 1. 前台服务方案 class OptimizedForegroundService : Service() {private val notificationId 1private val channel…...

Mysql insert一条数据的详细过程
以下是MySQL在接收到INSERT语句后存储数据的详细过程解析,结合存储引擎(以InnoDB为例)和物理存储机制分步说明。 一、SQL解析与事务启动 1.语法解析 MySQL首先解析INSERT语句,验证字段是否存在、数据类型是否匹配、约束…...

线性DP:最长上升子序列(子序列可不连续,子数组必须连续)
目录 Q1:简单遍历 Q2:变式(加大数据量) Q1:简单遍历 Dp问题 状态表示 f(i,j) 集合所有以第i个数结尾的上升子序列集合-f(i,j)的值存的是什么序列长度最大值max- 状态计算 (其实质是集合的划分)…...

C语言之文本加密程序设计
🌟 嗨,我是LucianaiB! 🌍 总有人间一两风,填我十万八千梦。 🚀 路漫漫其修远兮,吾将上下而求索。 文本加密程序设计 摘要:本文设计了一种文本加密程序,旨在提高信息安…...

生成器模式深入解析与 Spring 源码应用
摘要 本文以生成器模式为研究对象,采用通俗易懂的表述方式,详细阐释其核心概念与运行机制。通过构建游戏角色创建、电商订单生成等实际 Java 案例,直观呈现该模式在复杂对象构建中的应用优势。同时,深入剖析 Spring 框架源码&…...

云效部署实现Java项目自动化部署图解
前言 记录下使用云效部署Java项目,实现java项目一键化自动化部署。 云效流程说明: 1.云效拉取最新git代码后 2.进行maven编译打包后,上传到指定服务器目录 3.通过shell脚本,先kill java项目后,通过java -jar 启动项…...

0801ajax_mock-网络ajax请求1-react-仿低代码平台项目
0 vite配置proxy代理 vite.config.ts代码如下图所示: import { defineConfig } from "vite"; import react from "vitejs/plugin-react";// https://vite.dev/config/ export default defineConfig({plugins: [react()],server: {proxy: {&qu…...

基于Python智能体API的Word自动化排版系统:从零构建全流程模块化工作流与版本控制研究
基于Python智能体API的Word自动化排版系统:从零构建全流程模块化工作流与版本控制实践研究 1. 引言2. 研究背景与意义3. 自动排版工作流的设计原理3.1 文档内容提取与解析3.2 样式参数与格式化规则3.3 智能体API接口调用3.4 自动生成与批量处理3.5 与生成式AI的协同4. 系统架构…...

Java【网络原理】(4)HTTP协议
目录 1.前言 2.正文 2.1自定义协议 2.2HTTP协议 2.2.1抓包工具 2.2.2请求响应格式 2.2.2.1URL 2.2.2.2urlencode 2.2.3认识方法 2.2.3.1GET与POST 2.2.3.2PUT与DELETE 2.2.4请求头关键属性 3.小结 1.前言 哈喽大家好啊,今天来继续给大家带来Java中网络…...

每天学一个 Linux 命令(27):head
可访问网站查看,视觉品味拉满: http://www.616vip.cn/27/index.html head 是 Linux 中用于查看文件开头部分内容的命令,默认显示文件前 10 行,适合快速预览文件结构或日志头部信息。 命令格式 head [选项] [文件]常用选项 选项说明-n <行数>指定显示前 N 行(如…...

【2025软考高级架构师】——计算机系统基础(7)
摘要 本文主要介绍了计算机系统的组成,包括硬件和软件两大部分。硬件由处理器、存储器、总线、接口和外部设备等组成,软件则涵盖系统软件和应用软件。文章还详细阐述了冯诺依曼计算机的组成结构,包括 CPU、主存储器、外存等,并解…...

自定义 strlen 函数:递归实现字符串长度计算
目录 自定义 strlen 函数:递归实现字符串长度计算 一.引言 二.代码呈现 三.代码结构与功能概述 1.自定义 my_strlen 函数 1.函数参数与功能 2.代码逻辑分析 1.参数有效性检查: 2.递归计算字符串长度: 2.main 函数 1.变量定义 2.函…...

LeetCode 打家劫舍+删除并获得点数
题目描述 打家劫舍题目传送门1 删除并获得点数传送门2 思路 这两道题看似毫无关系,但竟然可以用桶数组联系起来!! 先说打家劫舍这道题 限制条件是不能走相邻的屋,再联想到跳台阶(走一格或两格)&#x…...

图解MCP:Model Context Protocol
🧠 向所有学习者致敬! “学习不是装满一桶水,而是点燃一把火。” —— 叶芝 我的博客主页: https://lizheng.blog.csdn.net 🌐 欢迎点击加入AI人工智能社区! 🚀 让我们一起努力,共创…...
