位运算---总结
位运算
基础
1. & 运算符 : 有 0 就是 0
2. | 运算符 : 有 1 就是 1
3. ^ 运算符 : 相同为0 相异为1 and 无进位相加
-
位运算的优选级
不用在意优先级,能加括号就加括号 -
给一个数 n ,确定它的二进制位中第 x 位是 0 还是 1?
规定: 题中所说的第x位指:int 在32位机器下4个字节32位,从右向左依次增加,从0位开始,即 第 0 位 到第 31 位.
(n >> x) & 1
- 将一个数 n 的二进制位表示的第 x 位修改为 1
n |= (1 << x)
- 将一个数 n 的二进制表示的 第 x 位修改为 0
n &= ~(1 << x)
- 提取一个数 n 二进制表示中最右侧的1
n & -n;
-n : 将最右侧的1左边的区域全部变为相反数,右边的1的数不变(本来就是0)0 1 1 0 1 0 1 0 0 0
~ 1 0 0 1 0 1 0 1 1 1
+1 1 0 0 1 0 1 1 0 0 0
n: 0 1 1 0 1 0 1 0 0 0
------------------------0 0 0 0 0 0 1 0 0 0
- 干掉一个数( n )二进制表示中最右侧的1
n &= (n -1)
- 异或(^)运算的运算律
1. a ^ 0 = a;
2. a ^ a = 0; 消消乐
3. a ^ b ^ c = a ^ (b ^ c) 符合交换律和结合律异或
无进位相加解释:
1 0 1 1 0 1 0
0 0 1 0 1 0 1
1 0 1 0 0 0 0
-------------
0 0 1 1 1 1 1 --> 两个 1 会消消乐(本质就是1的抵消), 即无进位相加
题目练习
191.位1的个数
思路一:依次判断每个位是否为1,为 1 ans++;
class Solution {
public:int hammingWeight(int n) {int ans = 0;int sum = 32;for(int i = 0; i < 32; i++){if((n >> i) & 1){ans++;}}return ans;}
};思路二:依次消除最低位的 1, 消除一次 ans++;
class Solution {
public:int hammingWeight(int n) {int ans = 0;while(n){n &= (n -1);ans++;}return ans;}
};
338. 比特位计数
思路:依次消除最低位的 1, 消除一次 count++; 对每个数字统计一次即可
class Solution {
public:vector<int> countBits(int n) {vector<int> ans;for(int i = 0; i <= n; i++){int count = 0;int temp = i;while(temp){temp &= (temp - 1);count++;}ans.push_back(count);}return ans;}
};
461. 汉明距离
//思路:先异或(相同为0相异为1)后统计1的个数
class Solution {
public:int hammingDistance(int x, int y) {x ^= y;int ans = 0;while(x){x &= (x -1);++ans;}return ans;}
};
136. 只出现一次的数字
//思路:利用异或运算规律:
// 1. a ^ a = 0;
// 2. a ^ 0 = a
// 3. 交换律和结合律
class Solution {
public:int singleNumber(vector<int>& nums) { int ans = 0;for(int iter : nums){ans ^= iter;}return ans;}
};
260. 只出现一次的数字 III
//思路:利用异或的规律,将所有数据异或一次,结果一定是只出现一次的两个元素异或后的结果,然后利用异或的相同为 0 相异为 1,并用最低位 1 来区分两个只出现一次的元素,划分为两个集合(此时每个集合中只有一个数出现一次,其他数都出现了两次),分别异或即可得到结果
class Solution {
public:vector<int> singleNumber(vector<int>& nums) {unsigned int xor_all = 0; //为什么使用unsigned int ?//使用int可能会导致溢出//unsigned int 自动会进行模运算,保证结果始终在unsigned int 表示范围内//int: (-2^31 到 2^31 - 1)//unsigned int: (0 ~ 2^32 -1)for(int iter : nums){xor_all ^= iter;}//获取异或结果的最低位为 1 的位 int lowbit = xor_all & (-xor_all);vector<int> ans(2);for(int x : nums){if((x & lowbit) == 0){ans[1] ^= x;}else{ans[0] ^= x;}}return ans;}
};
面试题 01.01. 判定字符是否唯一
思路:使用hash表统计每个字符出现的次数,然后遍历hash表即可
class Solution {
public:bool isUnique(string astr) {unordered_map<char,int> hash;for(int i = 0; i < astr.size(); i++){hash[astr[i]]++;}for(auto iter : hash){if(iter.second > 1){return false;}}return true;}
};class Solution {
public:bool isUnique(string astr) {//利用位图思想来解决问题if(astr.size() > 26){return false;}int bitmap = 0;for(char c : astr){int n = c - 'a';//判断字符是否已经出现过if(bitmap & (1 << n)){return false;} else{bitmap |= (1 << n);}}return true;}
};
268. 丢失的数字
//利用异或的规则:将0~n的数字和 nums中的数字都异或一次结果即为没有出现的那个数,其他数都出现了两次
class Solution {
public:int missingNumber(vector<int>& nums) {unsigned int xor_all = 0;int n = nums.size();for(int i = 0; i <= n; i++){xor_all ^= i;}for(int x : nums){xor_all ^= x;}return xor_all;}
};
371. 两整数之和
//思路:先使用无进位相加,计算进位,无进位相加直到进位为0
class Solution {
public:int getSum(int a, int b) {while(b != 0){int x = a ^ b;//计算无进位相加int carry = ( a & b) << 1; ;//计算进位a = x;b = carry;}return a;}
};
137. 只出现一次的数字 II
//思路:统计每个数字第i位的和sum, sum %= 3 即可判断只出现一次的数字第i位
//3n 0 + 0 = 0 %=3 == 0
//3n 0 + 1 = 1 %=3 == 1
//3n 1 + 1 = 3n + 1 %3 == 1
//3n 1 + 0 = 3n %=3 == 1 -->此方法可推广到n,即除某个元素只出现一次外,其他元素都出现了n次,%=n 即可判断只出现一次的数字的第i位
class Solution {
public:int singleNumber(vector<int>& nums) {int ans = 0;for(int i = 0; i < 32; i++){int sum = 0;for(int x : nums){if(x & (1 << i)){++sum;}}sum %= 3; if(sum == 1){ans |= (1 << i);}}return ans;}
};
面试题 17.19. 消失的两个数字
//思路:将所有数字全部异或,转换为题目只出现了一次的数字3
class Solution {
public:vector<int> missingTwo(vector<int>& nums) {unsigned int xor_all = 0;int n = nums.size();for(int x : nums){xor_all ^= x;}for(int i = 1; i <= n+2; i++){xor_all ^= i;}//计算最低位为1的位int lowbit = xor_all & (-xor_all);vector<int> ans(2);for(int x : nums){if((lowbit & x) == 0){ans[0] ^= x;}else{ans[1] ^= x;}}for(int i = 1; i <= n+2; i++){if((lowbit & i) == 0){ans[0] ^= i;}else{ans[1] ^= i;}}return ans;}
};
结束!
相关文章:

位运算---总结
位运算 基础 1. & 运算符 : 有 0 就是 0 2. | 运算符 : 有 1 就是 1 3. ^ 运算符 : 相同为0 相异为1 and 无进位相加位运算的优选级 不用在意优先级,能加括号就加括号给一个数 n ,确定它的二进制位中第 x 位是 0 还是 1? 规定: 题中所说的第x位指:int 在32位机器下4个…...

2. 什么是最普通的自动化“裸奔状态”?
什么是最普通的自动化"裸奔状态"?从大厂案例看测试代码的生存困境 一个典型的"裸奔代码"示例 # 打开目标网站 driver.get(http://test-site.com/login-page)# 登录操作 driver.find_element_by_id(user).send_keys(tester) driver.find_eleme…...
)
头歌java课程实验(函数式接口及lambda表达式)
第1关:利用lambda表达式对Book数组按多个字段进行排序 任务描述 本关任务:利用Comparator接口完成对Book数组同时按多个字段进行排序。 编程要求 1、本任务共有三个文件,可查看各文件的内容 2、无需修改SortBy.java枚举文件及Book.java类文…...

微信小程序三种裁剪动画有效果图
效果图 .wxml <image class"img inset {{status?action1:}}" src"{{src}}" /> <image class"img circle {{status?action2:}}" src"{{src}}" /> <image class"img polygon {{status?action3:}}" src&quo…...

C语言笔记(鹏哥)上课板书+课件汇总(结构体)-----数据结构常用
结构体 目录: 1、结构体类型声明 2、结构体变量的创建和初始化 3、结构体成员访问操作符 4、结构体内存对齐*****(重要指数五颗星) 5、结构体传参 6、结构体实现位段 一、结构体类型声明 其实在指针中我们已经讲解了一些结构体内容了&…...

git清理--解决.git文件过大问题
背景:为什么.git比我仓库中的文件大很多 为什么我的git中只有一个1KB的README,但是.git却又1G多?当我想把这个git库push到gitee时,还会报错: 根据报错信息,可看出失败的原因是:有文件的大小超过…...

Jetson Orin NX 部署YOLOv12笔记
步骤一.创建虚拟环境 conda create -n yolov12 python3.8.20 注意:YOLOv12/YOLOv11/YOLOv10/YOLOv9/YOLOv8/YOLOv7a/YOLOv5 环境通用 步骤二.激活虚拟环境 conda activate yolov12 #激活环境 步骤三.查询Jetpack出厂版本 Jetson系列平台各型号支持的最高Jetp…...

微服务2--服务治理与服务调用
前言 :本文主要阐述微服务架构中的服务治理,以及Nacos环境搭建、服务注册、服务调用,负载均衡以及Feign实现服务调用。 服务治理 服务治理是微服务架构中最核心最基本的模块。用于实现各个微服务的自动化注册与发现。 服务注册:在…...

Arduino示例代码讲解:Project 08 - Digital Hourglass 数字沙漏
Arduino示例代码讲解:Project 08 - Digital Hourglass 数字沙漏 Project 08 - Digital Hourglass 数字沙漏程序功能概述功能:硬件要求:输出:代码结构全局变量`setup()` 函数`loop()` 函数计时和点亮LED:读取倾斜开关状态:重置LED和计时器:运行过程注意事项Project 08 - …...

python生成项目依赖文件requirements.txt
文章目录 通过pip freeze去生成通过pipreqs去生成 通过pip freeze去生成 pip freeze > requirements.txt会将整个python的Interceptor的环境下lib包下所有的依赖都生成到这个文件当中,取决于我们使用的python的版本下所有的安装包。不建议使用这种方式ÿ…...

C语言之高校学生信息快速查询系统的实现
🌟 嗨,我是LucianaiB! 🌍 总有人间一两风,填我十万八千梦。 🚀 路漫漫其修远兮,吾将上下而求索。 C语言之高校学生信息快速查询系统的实现 目录 任务陈述与分析 问题陈述问题分析 数据结构设…...
:打破创业幻想,拥抱数据驱动)
精益数据分析(7/126):打破创业幻想,拥抱数据驱动
精益数据分析(7/126):打破创业幻想,拥抱数据驱动 在创业的道路上,我们都怀揣着梦想,但往往容易陷入自我编织的幻想中。我希望通过和大家一起学习《精益数据分析》,能帮助我们更清醒地认识创业过…...

Spring Boot 项目中发布流式接口支持实时数据向客户端推送
1、pom依赖添加 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-webflux</artifactId></dependency>2、事例代码 package com.pojo.prj.controller;import com.pojo.common.core.utils.String…...

Ubuntu安装MySQL步骤及注意事项
一、安装前准备 1. 系统更新:在安装 MySQL 之前,确保你的 Ubuntu 系统软件包是最新的,这能避免因软件包版本问题导致的安装错误,并获取最新的安全补丁。打开终端,执行以下两条命令: sudo apt update sudo …...

【网络篇】从零写UDP客户端/服务器:回显程序源码解析
大家好呀 我是浪前 今天讲解的是网络篇的第四章:从零写UDP客户端/服务器:回显程序源码解析 从零写UDP客户端/服务器:回显程序源码解析 UDP 协议特性核心类介绍 UDP的socket应该如何使用:1: DatagramSocket2: DatagramPacket回…...
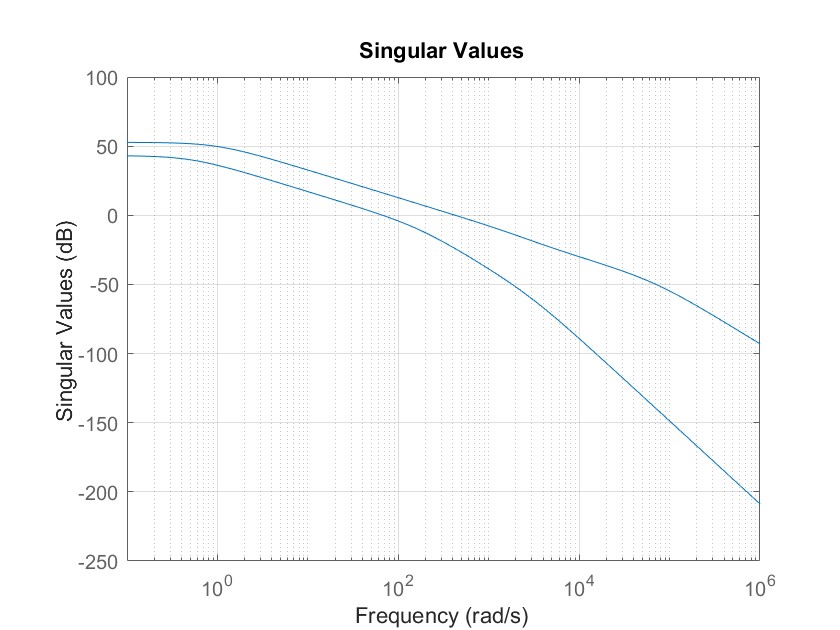
MATLAB 控制系统设计与仿真 - 38
多变量系统控制器设计实例1 考虑如下给出的多变量系统模型: 考虑混合灵敏度问题,引入加权矩阵: 设计鲁棒控制器,并绘制闭环系统的阶跃响应曲线及开环系统的奇异值曲线。 MATLAB代码如下: clear all;clc; stf(s); g1…...

轻量化高精度的视频语义分割
Video semantic segmentation (VSS)视频语义分割 Compact Models(紧凑模型) 在深度学习中,相对于传统模型具有更小尺寸和更少参数数量的模型。这些模型的设计旨在在保持合理性能的同时,减少模型的计算和存储成本。 紧凑模型的设计可以涉及以下一些技术: 深度剪枝(Deep…...

Spring Boot 版本与对应 JDK 版本兼容性
Spring Boot 版本与对应 JDK 版本兼容性 以下是 Spring Boot 主要版本与所需 JDK 版本的对应关系,以及长期支持(LTS)信息: 最新版本对应关系 (截至2024年) Spring Boot 版本发布日期支持的 JDK 版本备注3.2.x (最新)2023-11JDK 17-21推荐使用 JDK 173…...

[密码学实战]详解gmssl库与第三方工具兼容性问题及解决方案
[密码学实战]详解gmssl库与第三方工具兼容性问题及解决方案 引言 国密算法(SM2/SM3/SM4)在金融、政务等领域广泛应用,但开发者在集成gmssl库实现SM2签名时,常遇到与第三方工具(如OpenSSL、国密网关)验证不…...

JavaScript模块化开发:CommonJS、AMD到ES模块
引言 在Web开发的早期阶段,JavaScript代码通常被编写在一个庞大的文件中或分散在多个脚本标签里,这种方式导致了全局变量污染、依赖关系难以管理、代码复用困难等问题。随着Web应用日益复杂,模块化编程成为了解决这些问题的关键。本文将带您…...

【k8s系列1】一主两从结构的环境准备
环境准备 虚拟机软件准备及安装,这里就不详细展开了,可以看文章:【一、虚拟机vmware安装】 linux环境准备及下载,下载镜像centOS7.9,以前也有写过这个步骤的文章,可以看:【二、安装centOS】 开始进入正题…...

dubbo SPI插件扩展点使用
参考:SPI插件扩展点 Dubbo SPI概述 使用IoC容器帮助管理组件的生命周期、依赖关系注入等是很多开发框架的常用设计,Dubbo中内置了一个轻量版本的IoC容器,用来管理框架内部的插件,实现包括插件实例化、生命周期、依赖关系自动注入…...

青少年编程与数学 02-016 Python数据结构与算法 26课题、生物信息学算法
青少年编程与数学 02-016 Python数据结构与算法 26课题、生物信息学算法 一、序列比对算法二、基因表达分析算法三、蛋白质结构预测算法四、系统生物学模型构建算法五、单细胞分析算法六、遗传关联分析算法七、机器学习与数据挖掘算法八、数据可视化算法九、代谢组学分析算法十…...

【Rust 精进之路之第2篇-初体验】安装、配置与 Hello Cargo:踏出 Rust 开发第一步
系列: Rust 精进之路:构建可靠、高效软件的底层逻辑 **作者:**码觉客 发布日期: 2025-04-20 引言:磨刀不误砍柴工,装备先行! 在上一篇文章中,我们一起探索了 Rust 诞生的缘由&…...
)
洛谷题目:P7775 [COCI 2009/2010 #2] VUK 题解 (本题简)
题目传送门: P7775 [COCI 2009/2010 #2] VUK - 洛谷 (luogu.com.cn) 前言: 这道题的核心目标是找出狼从起点 V 到终点 J 的路径,使得狼在途中离它最近的树的距离的最小值最大。下面为大家详细讲解: #整体思路概述: 这道题我们可以采用“先计算距离,再来二分查找”的…...

腾讯旗下InstantCharacter框架正式开源 可高度个性化任何角色
目前基于学习的主题定制方法主要依赖于 U-Net 架构,但其泛化能力有限,图像质量也大打折扣。同时,基于优化的方法需要针对特定主题进行微调,这不可避免地会降低文本的可控性。为了应对这些挑战,我们提出了 “即时角色”…...

Python爬虫实战:获取fenbi网最新备考资讯
一、引言 1.1 研究背景 伴随互联网技术的迅猛发展,在线教育平台积累了海量备考数据。以粉某网为例,其备考数据涵盖考试资讯、备考资料、用户评价等,对备考者意义重大。然而,获取并分析这些数据颇具挑战,需借助先进的爬虫技术和数据分析方法。 1.2 研究目的 本研究旨在…...

详讲Linux下进程等待
3.进程等待 引言:什么是进程等待 想象有两个小伙伴,一个是 “大强”(父进程 ),一个是 “小强”(子进程 )。大强给小强安排了任务,比如去收集一些石头。 …...

JBoss + WildFly 本地开发环境完全指南
JBoss WildFly 本地开发环境完全指南 本篇笔记主要实现在本地通过 docker 创建 JBoss 和 WildFly 服务器这一功能,基于红帽的禁制 EAP 版本的重新分发,所以我这里没办法放 JBoss EAP 的 zip 文件。WildFly 是免费开源的版本,可以在红帽官网找…...

【网络原理】TCP协议如何实现可靠传输(确认应答和超时重传机制)
目录 一. TCP协议 二. 确定应答 三. 超时重传 一. TCP协议 1)端口号 源端口号:发送方端口号目的端口号:接收方端口号 16位(2字节)端口号,可以表示的范围(0~65535) 源端口和目的…...
