【数据结构和算法】3. 排序算法
本文根据 数据结构和算法入门 视频记录
文章目录
- 1. 排序算法
- 2. 插入排序 Insertion Sort
- 2.1 概念
- 2.2 具体步骤
- 2.3 Java 实现
- 2.4 复杂度分析
- 3. 快排 QuickSort
- 3.1 概念
- 3.2 具体步骤
- 3.3 Java实现
- 3.4 复杂度分析
- 4. 归并排序 MergeSort
- 4.1 概念
- 4.2 递归具体步骤
- 4.3 Java实现
- 4.4 复杂度分析
1. 排序算法
搜索是计算机中非常重要的步骤,但是从无序的数据中寻找特定的数字往往很难,我们之前提到的二分查找只能运用在排好序的数组中。所以排序算法是一个很重要的工作,如果我们能够将数值排好序,那么当我们寻找特定数值的时候,能省下不少功夫。
排序算法有很多,每种排序算法各有优缺点:

在这章节中,我们就来学习其中最经典的三种排序方法:插入排序Insertion Sort,快排Quick Sort,归并排序Merge Sort。
2. 插入排序 Insertion Sort
2.1 概念
插入排序是一种简单直观的排序算法。在插入排序中,我们从前到后依次处理未排好序的元素,对于每个元素,我们将它与之前排好序的元素进行比较,找到对应的位置后并插入。本质上,对于每一个要被处理的元素,我们只关心它与之前元素的关系,当前元素之后的元素我们下一轮才去处理。

在实现上,每个元素和之前元素比较的过程,是一个从后到前扫描的过程。在扫描时,我们将已排好序的元素先后挪位,为新的元素提供插入位置。这也叫做 in-place 排序,这样我们就不需要额外的内存空间了。
2.2 具体步骤
- 从第二个元素(第一个要被排序的新元素)开始,从后向前扫描之前的元素序列
- 如果当前扫描的元素大于新元素,将扫描元素移动到下一位
- 重复步骤2,直到找到一个小于或者等于新元素的位置
- 将新元素插入到该位置
- 对于之后的元素重复步骤1~4
伪代码 pseudo code
function insertion_sort(array[]):for (i = 1; i < array.length; i++):cur = array[i]j = i - 1while (j >= 0 && array[j] > cur):array[j + 1] = array[j]j--array[j + 1] = cur
2.3 Java 实现
public void insertionSort(int[] array) {for(int i = 1; i < array.length; i++) {int cur = array[i];int insertionIndex = i - 1;while(insertionIndex >= 0 && array[insertionIndex] > cur) {array[insertionIndex + 1] = array[insertionIndex];insertionIndex--;}array[insertionIndex + 1] = cur;}
}
2.4 复杂度分析
时间复杂度:O(n²)
空间复杂度:O(1)
「时间复杂度」在此算法中就是计算比较的次数,第一个元素我们需要比较1次,第二个元素2次,对于第n个元素,我们需要和之前的元素比较n次,比较总数量也就是 1 + 2 + … + n = n(n + 1) / 2
≈ n^2。因为我们调换位置时采用「原地操作」(in place),所以不需要额外空间,既空间复杂度为O(1)。
3. 快排 QuickSort
3.1 概念
快排是一种分治(Divide and Conquer)算法,在这种算法中,我们把大问题变成小问题,然后将小问题逐个解决,当小问题解决完时,大问题也迎刃而解。
快排的基本概念就是选取一个目标元素,然后将目标元素放到数组中正确的位置。然后根据排好序后的元素,将数组切分为两个子数组,用相同的方法,在没有排好序的范围使用相同的操作。

3.2 具体步骤
- 对于当前的数组,取最后一个元素当做基准数(pivot)
- 将所有比基准数小的元素排到基准数之前,比基准数大的排在基准数之后
- 当基准数被放到准确的位置之后,根据基数数的位置将元素切分为前后两个子数组
- 对子数组采用步骤1~4的递归操作,直到子数组的长度小于等于1为止
伪代码(Pseudo code)
function quickSort(array[], left, right):partitionIndex = partition(array, left, right)quickSort(array, left, partitionIndex - 1)quickSort(array, partitionIndex + 1, right)function partition(array[], left, right):pivot = array[right]smallerElementIndex = leftbiggerElementIndex = right - 1while(true):while(smallerElementIndex < right && array[smallerElementIndex] <= pivot):smallerElementIndex++while(biggerElementIndex >= left && array[biggerElementIndex] > pivot):rightIndex--if(smallerElementIndex > biggerElementIndex) breakswap(array, smallerElementIndex, biggerElementIndex)# Now array[smallerElementIndex] is the first element bigger than pivotswap(array, smallerElementIndex, right)return smallerElementIndex
3.3 Java实现
public void quickSort(int[] array, int left, int right) {if(left >= right) return;int partitionIndex = partition(array, left, right);quickSort(array, left, partitionIndex - 1);quickSort(array, partitionIndex + 1, right);
}
public int partition(int[] array, int left, int right) {int pivot = array[right];int leftIndex = left;int rightIndex = right - 1;while(true) { while(leftIndex < right & array[leftIndex] <= pivot) {leftIndex++;}while(rightIndex >= left && array[rightIndex] > pivot) {rightIndex--;}if (leftIndex > rightIndex) break;swap(array, leftIndex, rightIndex);}swap(array, leftIndex, right); // swap pivot to the right positionreturn leftIndex;
}
public void swap(int[] array, int left, int right) {int temp = array[left];array[left] = array[right];array[right] = temp;
}
3.4 复杂度分析
时间复杂度:O(n^2),平均时间复杂度:O(nlogN)
空间复杂度:O(n),平均空间复杂度:O(logN)
在最坏的情况下,如果元素一开始就是从大到小倒序排列的,那么我们每个元素都需要调换,时间复杂度就是O(n^2)。当正常情况下,我们不会总碰到这样的情况,假设我们每次都找到一个中间的基准数,那么我们需要切分logN次,每层的划分(Partition)是O(N),平均时间复杂度就是O(nlogN)。空间的复杂度取决于递归的层数,最糟糕的情况我们需要O(N)层,一般情况下,我们认为平均时间复杂度是O(logN)。
4. 归并排序 MergeSort
4.1 概念
归并排序也是一种基于归并操作的有效排序算法。在此算法中,我们将一个数组分为两个子数组,通过递归重复将数组切分到只剩下一个元素为止。然后将每个子数组中的元素排序后合并,通过不断合并子数组,最后就会拿到一个排好序的大数组。
归并排序和快排一样,也是一种分而治之算法,简单理解就是将大问题变为小问题,然后把所有小问题都解决掉,大问题就迎刃而解了。其中主要包括两个步骤:
- 切分步骤:将大问题变为小问题,通过递归解决更小的子问题。
- 解决步骤:将小问题的结果合并,以此找到大问题的答案。
以数组 [38, 27, 43, 3, 9, 82, 10] 为例,我们通过递归分组,之后原数组被分成长度小于等于2的子数组:
[38, 27], [43, 3], [9, 82], [10]
并将子数组中的元素排序好:
[27, 28], [3, 43], [9, 82], [10]
然后两两合并,归并成排好序的子数组:
[3, 27, 38, 43], [9, 10, 82]
最后将子数组合并为一个排好序的大数组:
[3, 9, 10, 27, 38, 43, 82]

4.2 递归具体步骤
- 递归切分当前数组
- 如果当前数组数量小于等于1,无需排序,直接返回结果
- 否则将当前数组分为两个子数组,递归排序这两个子数组
- 在子数组排序结束后,将子数组的结果归并成排好序的数组
伪代码 Pseudocode
function mergeSort(array[], start, end):if (end - start < 1) returnmid = (start + end) / 2mergeSort(array, start, mid)mergeSort(array, mid + 1, end);merge(array, start, mid, end)function merge(array[], start, mid, end):helper[] = array.copy()leftStart = start, rightStart = mid + 1while(leftStart <= mid || rightStart <= end):if(helper[leftStart] <= helper[rightStart]):array[start++] = helper[leftStart++]else:array[start++] = helper[rightStart++]if(leftStart <= mid): while(leftStart <= mid):array[start++] = helper[leftStart++]else:while(rightStart <= end):array[start++] = helper[rightStart++]
4.3 Java实现
public void mergeSort(int[] array) {int[] helper = copy(array);mergeSort(array, helper, 0, array.length - 1);return array;
}
public void mergeSort(int[] array, int[] helper, int left, int right) {if(right - left < 1) return;int mid = left + (right - left) / 2;mergeSort(array, helper, left, mid);mergeSort(array, helper, mid + 1, right);merge(array, helper, left, mid, right);
}
public void merge(int[] array, int[] helper, int left, int mid, int right) {for(int i = left; i <= right; i++) {helper[i] = array[i];}int leftStart = left;int rightStart = mid + 1;for (int i = left; i <= right; i++) { if (leftStart > mid) { array[i] = helper[rightStart++];} else if (rightStart > right) {array[i] = helper[leftStart++];} else if (helper[leftStart] < helper[rightStart]) {array[i] = helper[leftStart++];} else {array[i] = helper[rightStart++];}}
}
public int[] copy(int[] array) {int[] newArray = new int[array.length];for(int i = 0; i < array.length; i++) { newArray[i] = array[i];}return newArray;
}
4.4 复杂度分析
时间:O(nlogN)
空间:O(N)
在将大问题切分为小问题的过程中,我们每次都将数组切一半,所以需要logN次才能将数组切到一个元素,所以递归的层级就是logN。在每一层中,我们要对子数组进行归并,我们要扫描所有的元素,所以每一层需要N次扫描。那么,时间复杂度就是层级乘以每层的操作 = logN * N = O(NLogN)。在每一层中,我们需要一个临时的数组来存放原先的数据,然后在这个数组中扫描子数组的元素,并将其排好序放回原来的数组,所以空间复杂度就是O(N)。
相关文章:

【数据结构和算法】3. 排序算法
本文根据 数据结构和算法入门 视频记录 文章目录 1. 排序算法2. 插入排序 Insertion Sort2.1 概念2.2 具体步骤2.3 Java 实现2.4 复杂度分析 3. 快排 QuickSort3.1 概念3.2 具体步骤3.3 Java实现3.4 复杂度分析 4. 归并排序 MergeSort4.1 概念4.2 递归具体步骤4.3 Java实现4.4…...

LintCode第192题-通配符匹配
描述 给定一个字符串 s 和一个字符模式 p ,实现一个支持 ? 和 * 的通配符匹配。匹配规则如下: ? 可以匹配任何单个字符。* 可以匹配任意字符串(包括空字符串)。 两个串完全匹配才算匹配成功。 样例 样例1 输入: "aa&q…...

redis常用的五种数据类型
redis常用的五种数据类型 文档 redis单机安装redis数据类型-位图bitmap 说明 官网操作命令指南页面:https://redis.io/docs/latest/commands/?nameget&groupstring 常用命令 keys *:查看所有键exists k1 k2:键存在个数type k1&…...

Linux 进程与线程间通信方式及应用分析
Linux 进程与线程间通信方式及应用分析 文章目录 Linux 进程与线程间通信方式及应用分析 1. 管道(Pipe)1.1 匿名管道(Anonymous Pipe)示例代码:结果: 1.2 命名管道(FIFO)示例代码&am…...

AI日报 - 2024年04月22日
🌟 今日概览(60秒速览) ▎🤖 模型进展 | Google发布Gemini 2.5 Flash,强调低延迟与成本效益;Kling AI 2.0展示多轴运动视频生成;研究揭示SLM在知识图谱上优于LLM,RLHF在推理提升上存局限。 ▎💼…...

FreeRTos学习记录--2.内存管理
后续的章节涉及这些内核对象:task、queue、semaphores和event group等。为了让FreeRTOS更容易使用,这些内核对象一般都是动态分配:用到时分配,不使用时释放。使用内存的动态管理功能,简化了程序设计:不再需…...

HAL库(STM32CubeMX)——高级ADC学习、HRTIM(STM32G474RBT6)
系列文章目录 文章目录 系列文章目录前言存在的问题HRTIMcubemx配置前言 对cubemx的ADC的设置进行补充 ADCs_Common_Settings Mode:ADC 模式 Independent mod 独立 ADC 模式,当使用一个 ADC 时是独立模式,使用两个 ADC 时是双模式,在双模式下还有很多细分模式可选 ADC_Se…...

单例模式(线程安全)
1.什么是单例模式 单例模式(Singleton Pattern)是一种创建型设计模式,旨在确保一个类只有一个实例,并提供一个全局访问点来访问该实例。这种模式涉及到一个单一的类,该类负责创建自己的对象,同时确保只有单…...

FreeRTos学习记录--1.工程创建与源码概述
1.工程创建与源码概述 1.1 工程创建 使用STM32CubeMX,可以手工添加任务、队列、信号量、互斥锁、定时器等等。但是本课程不想严重依赖STM32CubeMX,所以不会使用STM32CubeMX来添加这些对象,而是手写代码来使用这些对象。 使用STM32CubeMX时&…...

基于大模型的血栓性外痔全流程风险预测与治疗管理研究报告
目录 一、引言 1.1 研究背景与目的 1.2 研究意义 二、血栓性外痔概述 2.1 定义与发病机制 2.2 临床表现与诊断方法 2.3 现有治疗手段综述 三、大模型在血栓性外痔预测中的应用原理 3.1 大模型技术简介 3.2 模型构建与训练数据来源 3.3 模型预测血栓性外痔的工作流程…...

进程控制(linux+C/C++)
目录 进程创建 写时拷贝 fork 进程终止 退出码 进程退出三种情况对应退出信号 :退出码: 进程退出方法 进程等待 两种方式 阻塞等待和非阻塞等待 小知识 进程创建 1.在未创建子进程时,父进程页表对于数据权限为读写,对于…...

C++如何处理多线程环境下的异常?如何确保资源在异常情况下也能正确释放
多线程编程的基本概念与挑战 多线程编程的核心思想是将程序的执行划分为多个并行运行的线程,每个线程可以独立处理任务,从而充分利用多核处理器的性能优势。在C中,开发者可以通过std::thread创建线程,并使用同步原语如std::mutex、…...

TensorBoard如何在同一图表中绘制多个线条
1. 使用不同的日志目录 TensorBoard 会根据日志文件所在的目录来区分不同的运行。可以为每次运行指定一个独立的日志目录,TensorBoard 会自动将这些目录中的数据加载并显示为不同的运行。 示例(TensorFlow): import tensorflow…...

微软Entra新安全功能引发大规模账户锁定事件
误报触发大规模锁定 多家机构的Windows管理员报告称,微软Entra ID新推出的"MACE"(泄露凭证检测应用)功能在部署过程中产生大量误报,导致用户账户被大规模锁定。这些警报和锁定始于昨夜,部分管理员认为属于误…...

基于FPGA的一维时间序列idct变换verilog实现,包含testbench和matlab辅助验证程序
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 4.1 DCT离散余弦变换 4.2 IDCT逆离散余弦变换 4.3 树结构实现1024点IDCT的原理 5.算法完整程序工程 1.算法运行效果图预览 (完整程序运行后无水印) matlab仿真结果 FPGA仿真结果 由于FP…...
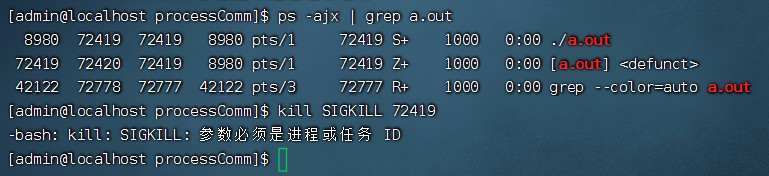
Linux进程5-进程通信常见的几种方式、信号概述及分类、kill函数及命令、语法介绍
目录 1.进程间通信概述 1.1进程通信的主要方式 1.2进程通信的核心对比 2.信号 2.1 信号的概述 2.1.1 信号的概念 2.2信号的核心特性 2.3信号的产生来源 2.4信号的处理流程 2.5关键系统调用与函数 2.6常见信号的分类及说明 2.6.1. 标准信号(Standard Sig…...

[架构之美]一键服务管理大师:Ubuntu智能服务停止与清理脚本深度解析
[架构之美]一键服务管理大师:Ubuntu智能服务停止与清理脚本深度解析 服务展示: 运行脚本: 剩余服务: 一、脚本设计背景与核心价值 在Linux服务器运维中,服务管理是日常操作的重要环节。本文介绍的智能服务管理脚本&a…...

C++算法(10):二叉树的高度与深度,(C++代码实战)
引言 在二叉树的相关算法中,高度(Height)和深度(Depth)是两个容易混淆的概念。本文通过示例和代码实现,帮助读者清晰区分二者的区别。 定义与区别 属性定义计算方式深度从根节点到该节点的边数根节点深度…...

k8s 基础入门篇之开启 firewalld
前面在部署k8s时,都是直接关闭的防火墙。由于生产环境需要开启防火墙,只能放行一些特定的端口, 简单记录一下过程。 1. firewall 与 iptables 的关系 1.1 防火墙(Firewall) 定义: 防火墙是网络安全系统&…...

Psychology 101 期末测验(附答案)
欢呼 啦啦啦~啦啦啦~♪(^∇^*) 终于考过啦~ 开心(*^▽^*) 撒花✿✿ヽ(▽)ノ✿ |必须晒下证书: 判卷 记录下判卷,还是错了几道,填空题2道压根填不上。惭愧~ 答案我隐藏了,实在想不出答案的朋友可以留言,不定时回复。 建议还是认认真真的学习~认认真真的考试~,知识就…...
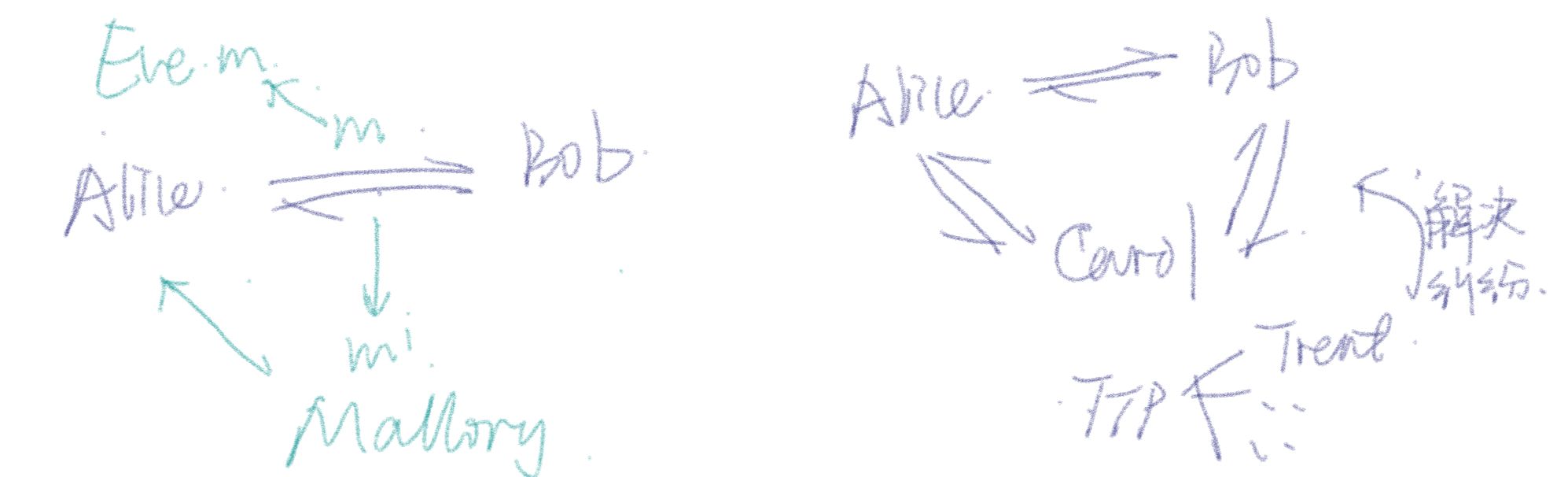
安全协议分析概述
一、概念 安全协议(security protocol),又称密码协议。是以密码学为基础的消息交换协议,在网络中提供各种安全服务。(为解决网络中的现实问题、满足安全需求) 1.1 一些名词 那什么是协议呢? …...

基础学习:(7)nanoGPT 剩下的细节
文章目录 前言3 继续巴拉结构3.1 encode 和 embedding3.2 全局layernorm3.3 lm_head(language modeling) 和 softmax3.4 softmax 和 linear 之间的 temperature和topk3.5 weight tying 前言 在 基础学习:(6)中, 在运行和训练代码基础上,向代…...

【HDFS】verifyEC命令校验EC数据正确性
verifyEC命令是HDFS里用于验证EC文件正确性的一个工具。这是一个非常实用的工具,能帮助我们确定EC的数据内容是否正确,并且如果不正确的话,还有可能会触发reportBadBlock给NN,让NN进行块的重构。 本文先介绍一下verifyEC命令的使用方法,再描述其实现原理细节。 一、命令…...

YOLO11改进,尺度动态损失函数Scale-based Dynamic Loss,减少标签不准确对损失函数稳定性的影响
在目标检测领域,标签噪声与尺度敏感问题始终是制约模型性能提升的"阿喀琉斯之踵"。2025年CVPR最佳论文提出的尺度动态损失函数(Scale-based Dynamic Loss, SDL),通过构建自适应损失调节机制,不仅实现了对YOLOv11检测精度的指数级提升,更重新定义了损失函数的设…...

Spark-SQL连接Hive总结及实验
一、核心模式与配置要点 1. 内嵌Hive 无需额外配置,直接使用,但生产环境中几乎不使用。 2. 外部Hive(spark-shell连接) 配置文件:将hive-site.xml(修改数据库连接为node01)、core-site.xml、…...

ROS 2的跨平台优势:国产芯片与Ubuntu系统的深度协同
一、国产硬件全场景适配:从教育到工业的ROS 2革命 瑞芯微三剑客性能解析 芯片架构特性ROS 2优化方案典型延迟/算力RK3399双核A72四核A53启用rmw_fastrtps内存池隔离通信延迟≤1.5msRK3588四核A766TOPS NPUrknn_ros2中间件实现算法热加载目标检测15ms4KRK3576六核A…...

Linux Wlan-四次握手(eapol)框架流程
协议基础 基于 IEEE 802.1X 标准实现的协议 抓包基础 使用上一章文章的TPLINK wn722n v1网卡在2.4G 频段抓包(v2、v3是不支持混杂模式的) eapol的四个交互流程 根据不同的认证模式不同,两者的Auth流程有所不同,但是握手流程基…...

web组件和http协议
1.web组件 2.自定义元素 3.影子DOM 4.HTML模板 5.http协议 6.tcp ip协议...

软件工程师中级考试-上午知识点总结(下)
6. 知识产权和标准化 软件著作权客体:指的是受软件著作权保护的对象,即计算机程序和相关文档。知识产权具有严格的地域性。不受保护期限制:著名权、修改权、保护作品完整权;注意的是,发表权受保护期限制。专利权在期满…...

IO流--字节流详解
IO流 用于读写数据的(可以读写文件,或网络中的数据) 概述: I指 Input,称为输入流:负责从磁盘或网络上将数据读到内存中去 O指Output,称为输出流,负责写数据出去到网络或磁盘上 因…...
