C++ round 函数笔记 (适用于算法竞赛)
在算法竞赛中,处理浮点数并将其转换为整数是常见的需求,round 函数是标准库提供的用于执行“四舍五入”到最近整数的工具。理解其工作方式和潜在问题对于避免错误至关重要。
1. 基本用法
头文件
要使用 round 函数,需要包含 <cmath> 头文件 (C++ 风格) 或 <math.h> (C 风格)。推荐使用 <cmath>。
#include <cmath>
#include <iostream>int main() {double num1 = 3.14;double num2 = 3.75;double num3 = -2.3;double num4 = -2.8;double num5 = 4.5;double num6 = -4.5;std::cout << "round(" << num1 << ") = " << std::round(num1) << std::endl; // 输出 3.0std::cout << "round(" << num2 << ") = " << std::round(num2) << std::endl; // 输出 4.0std::cout << "round(" << num3 << ") = " << std::round(num3) << std::endl; // 输出 -2.0std::cout << "round(" << num4 << ") = " << std::round(num4) << std::endl; // 输出 -3.0std::cout << "round(" << num5 << ") = " << std::round(num5) << std::endl; // 输出 5.0std::cout << "round(" << num6 << ") = " << std::round(num6) << std::endl; // 输出 -5.0return 0;
}
函数签名
round 函数有多个重载版本,接受不同的浮点类型:
double round(double x);
float roundf(float x); // C++11 起通常也有 round(float)
long double roundl(long double x); // C++11 起通常也有 round(long double)
在 C++ 中,通常可以直接使用 std::round(),编译器会根据参数类型自动选择合适的版本。
2. 核心规则:四舍五入到最近整数
round 函数将浮点数 x 舍入到最接近的整数值。
关键点:中间值处理 (Handling Halves)
- 当小数部分恰好为
0.5时,round函数遵循**“远离零”**的原则进行舍入。round(2.5)结果是3.0round(-2.5)结果是-3.0
- 这与某些其他编程语言或场景下的“四舍五入到偶数”(Round half to even / Banker’s rounding)不同。
3. 返回值类型
非常重要: round 函数的返回值类型仍然是浮点类型 (double, float, long double),即使它表示的是一个整数值。
如果你需要一个真正的整数类型 (int, long long 等),你需要进行显式类型转换。
#include <cmath>
#include <iostream>int main() {double val = 9.8;double rounded_val_double = std::round(val); // rounded_val_double 是 10.0 (double类型)// 显式转换为整数类型int rounded_val_int = static_cast<int>(rounded_val_double); // 推荐的C++风格转换long long rounded_val_ll = static_cast<long long>(std::round(1e10 + 0.3)); // 处理可能较大的数std::cout << "Rounded (double): " << rounded_val_double << std::endl;std::cout << "Rounded (int): " << rounded_val_int << std::endl;std::cout << "Rounded (long long): " << rounded_val_ll << std::endl; // 输出 10000000000// 注意潜在的溢出问题double large_val = 3e9; // 3 * 10^9int overflow_int = static_cast<int>(std::round(large_val));// 上一行可能导致整数溢出,结果未定义或取决于实现std::cout << "Potential overflow: " << overflow_int << std::endl;return 0;
}
4. 注意事项与竞赛技巧
a. 浮点数精度问题 (Floating-Point Precision Issues)
- 这是在算法竞赛中使用浮点数(包括
round)时最需要注意的问题。 - 计算机存储浮点数存在误差。一个看似是
x.5的数,在内存中可能是x.4999999999999999或x.5000000000000001。 - 这会导致
round的结果与预期不符。例如,你期望round(a / b * c)得到某个整数,但由于中间计算的精度损失,结果可能差一点点,导致round结果错误。
竞赛建议:
- 尽量避免浮点数: 如果问题可以通过全程使用整数算术解决,优先选择整数。例如,比较
a/b和c/d时,转换为比较a*d和c*b(注意溢出)。 - 使用 Epsilon (eps): 在判断浮点数相等或比较大小时,引入一个极小值
eps(如1e-8或1e-9)。例如,判断x是否接近整数n,可以用fabs(x - n) < eps。 - 谨慎使用
round: 只有在确实需要四舍五入,并且能接受微小误差带来的潜在风险时使用。
b. 手动实现整数“四舍五入”
有时,为了完全避免浮点误差,或者需要对整数运算结果进行类似四舍五入的操作,可以手动实现:
- 对于非负数
x:(int)(x + 0.5)或(long long)(x + 0.5) - 对于负数
x:(int)(x - 0.5)或(long long)(x - 0.5)
#include <iostream>
#include <vector> // 仅用于演示// 简化的手动四舍五入到整数 (int)
int manual_round_int(double x) {if (x >= 0.0) {return static_cast<int>(x + 0.5);} else {return static_cast<int>(x - 0.5);}
}// 更通用的手动四舍五入到长整型 (long long)
long long manual_round_ll(double x) {if (x >= 0.0) {return static_cast<long long>(x + 0.5);} else {return static_cast<long long>(x - 0.5);}
}int main() {std::cout << "Manual round(3.7): " << manual_round_int(3.7) << std::endl; // 4std::cout << "Manual round(3.2): " << manual_round_int(3.2) << std::endl; // 3std::cout << "Manual round(3.5): " << manual_round_int(3.5) << std::endl; // 4std::cout << "Manual round(-3.7): " << manual_round_int(-3.7) << std::endl; // -4std::cout << "Manual round(-3.2): " << manual_round_int(-3.2) << std::endl; // -3std::cout << "Manual round(-3.5): " << manual_round_int(-3.5) << std::endl; // -4// 示例:整数除法的四舍五入int a = 10, b = 3;// int result = a / b; // 结果是 3 (整数截断)// 要实现 a/b 的四舍五入结果:int rounded_div = static_cast<int>(static_cast<double>(a) / b + 0.5); // 先转double再加0.5// 或者,更推荐的整数算术方法(避免浮点):// rounded_div = (a + b / 2) / b; // 对于正数 a, bstd::cout << "Rounded division 10/3: " << rounded_div << std::endl; // 输出 3 (这里10/3=3.33, round是3)a = 11; b = 3; // 11/3 = 3.66...rounded_div = static_cast<int>(static_cast<double>(a) / b + 0.5);std::cout << "Rounded division 11/3: " << rounded_div << std::endl; // 输出 4return 0;
}
注意: 手动加 0.5 的方法仍然依赖于浮点数 x 的精度。如果 x 本身由于计算误差变成了 y.49999...,x + 0.5 可能会小于 y + 1.0,导致转换后仍为 y 而不是预期的 y+1。只有当你知道输入 x 是精确的,或者这种微小误差不影响结果时,它才是可靠的。
c. 考虑 ceil, floor, trunc
<cmath> 还提供了其他相关的取整函数:
ceil(x): 向上取整 (Ceiling)。返回>= x的最小整数值 (仍为浮点类型)。floor(x): 向下取整 (Floor)。返回<= x的最大整数值 (仍为浮点类型)。trunc(x): 向零取整 (Truncate)。直接截断小数部分,取整数部分 (仍为浮点类型)。等价于(double)((int)x)(如果x在int范围内且非负)。
根据具体需求选择合适的函数。
d. 输出格式化
有时,你可能只是为了输出一个四舍五入的整数,并不需要在程序内部使用这个整数值。可以使用 printf 的格式化功能:
#include <cstdio> // for printf
#include <cmath>int main() {double val = 9.8;double val2 = 9.4;double val3 = -9.8;printf("%.0f\n", val); // 输出 10 (%.0f 通常执行四舍五入,规则类似 round)printf("%.0f\n", val2); // 输出 9printf("%.0f\n", val3); // 输出 -10return 0;
}
注意: printf 的 %.0f 的具体舍入规则(尤其是对 0.5 的处理)可能依赖于 C++ 标准库的实现,但通常是“远离零”。最好通过测试确认。
5. 总结
std::round用于将浮点数四舍五入到最接近的整数(中间值0.5远离零),返回浮点类型。- 在竞赛中要高度警惕浮点数精度问题对
round结果的影响。 - 如果需要整数结果,必须进行显式类型转换 (
static_cast<int>,static_cast<long long>),并注意溢出。 - 优先考虑全程整数算术,如果可能的话。
- 了解
ceil,floor,trunc作为替代方案。 - 了解
printf("%.0f")可以用于格式化输出。 - 手动实现
(int)(x + 0.5)(非负) /(int)(x - 0.5)(负) 是避免调用库函数的一种方式,但仍受输入x精度影响。
在竞赛中,选择哪种方法取决于问题的具体要求、数据范围以及对精度的要求。理解各种方法的优缺点和潜在陷阱是取得好成绩的关键。
相关文章:
)
C++ round 函数笔记 (适用于算法竞赛)
在算法竞赛中,处理浮点数并将其转换为整数是常见的需求,round 函数是标准库提供的用于执行“四舍五入”到最近整数的工具。理解其工作方式和潜在问题对于避免错误至关重要。 1. 基本用法 头文件 要使用 round 函数,需要包含 <cmath>…...

1.5软考系统架构设计师:架构师的角色与能力要求 - 超简记忆要点、知识体系全解、考点深度解析、真题训练附答案及解析
超简记忆要点 角色职责 需求规划→架构设计→质量保障 能力要求 技术(架构模式/性能优化) 业务(模型抽象→技术方案) 管理(团队协作/风险控制) 知识体系 基础:CAP/设计模式/网络协议案例&am…...

单例模式与消费者生产者模型,以及线程池的基本认识与模拟实现
前言 今天我们就来讲讲什么是单例模式与线程池的相关知识,这两个内容也是我们多线程中比较重要的内容。其次单例模式也是我们常见设计模式。 单例模式 那么什么是单例模式呢?上面说到的设计模式又是什么? 其实单例模式就是设计模式的一种。…...

JAVA程序获取SVN提交记录
1.获取文件提交记录 private String userName "userName "; //svn账号 private String password "password "; //svn密码 private String urlString "urlString "; //svnurl 换成自己对应的svn信息 package com.tengzhi.common.dao;import…...

STM32配置系统时钟
1、STM32配置系统时钟的步骤 1、系统时钟配置步骤 先配置系统时钟,后面的总线才能使用时钟频率 2、外设时钟使能和失能 STM32为了低功耗,一开始是关闭了所有的外设的时钟,所以外设想要工作,首先就要打开时钟,所以后面…...

React 与 Vue:两大前端框架的深度对比
在前端开发领域,React 和 Vue 无疑是当下最受欢迎的两大框架。它们各自拥有独特的优势和特点,吸引了大量开发者。无论是初学者还是经验丰富的工程师,选择 React 还是 Vue 都是一个常见的问题。本文将从多个角度对 React 和 Vue 进行对比&…...

Node.js 学习入门指南
Node.js 学习入门指南 Node.js 是一种流行的开源、跨平台的 JavaScript 运行时环境,它使开发者能够在服务器端运行JavaScript代码。本篇文章旨在帮助初学者快速入门并掌握Node.js的基础知识和常用技巧。 一、什么是Node.js? 定义 Node.js 是一个基于…...

Java24新增特性
Java 24(Oracle JDK 24)作为Java生态的重要更新,聚焦AI开发支持、后量子安全、性能优化及开发者效率提升,带来20余项新特性和数千项改进。以下是核心特性的分类解析: 一、语言特性增强:简化代码与模式匹配 …...

Sentinel源码—6.熔断降级和数据统计的实现一
大纲 1.DegradeSlot实现熔断降级的原理与源码 2.Sentinel数据指标统计的滑动窗口算法 1.DegradeSlot实现熔断降级的原理与源码 (1)熔断降级规则DegradeRule的配置Demo (2)注册熔断降级监听器和加载熔断降级规则 (3)DegradeSlot根据熔断降级规则对请求进行验证 (1)熔断降级…...
Volcano 实战快速入门 (一)
一、技术背景 随着大型语言模型(LLM)的蓬勃发展,其在 Kubernetes (K8s) 环境下的训练和推理对资源调度与管理提出了前所未有的挑战。这些挑战主要源于 LLM 对计算资源(尤其是 GPU)的巨大需求、分布式任务固有的复杂依…...
)
快速体验tftp文件传输(嵌入式设备)
一、参考资料 Linux tftp 命令 | 菜鸟教程 Ubuntu最新版本(Ubuntu22.04LTS)安装Tftp服务及其使用教程-CSDN博客 Windows下的Tftpd32(Tftpd64)软件下载和使用教程-集成了Tftp服务器、客户端-CSDN博客 tftpd32 tftpd64文件传输安装和使用教程【图文并茂】-CSDN博客 二、快速…...

用交换机连接两台电脑,电脑A读取/写电脑B的数据
1、第一步,打开控制面板中的网络和共享中心,如下图配置,电脑A和电脑B均要配置; 注意:要保证电脑A和电脑B在同一子网掩码下,不同的IP地址; 2、在电脑上同时按‘CommandR’,在弹出的输…...

问道数码兽 怀旧剧情回合手游源码搭建教程(反查重优化版)
本文将对"问道数码兽"这一经典卡通风格回合制手游的服务端部署与客户端调整流程进行详细拆解,适用于具备基础 Windows 运维和手游源码调试经验的开发者参考使用。教程以实战为导向,基于原始说明内容重构优化,具备较高的内容查重避重…...

WLAN共享给以太网后以太网IP为169.254.xx.xx以及uboot无法使用nfs下载命令的的解决方案
WLAN共享网络给以太网,实际上是把以太网口当作一个路由器,这个路由器的IP是由WLAN给他分配的,169.254.xx.xx是windows设定的ip,当网络接口无法从上一级网络接口获得ip时,该网络接口的ip被设置为169.254 ,所…...
:环境安装与基础使用)
Gazebo 仿真环境系列教程(一):环境安装与基础使用
文章目录 一、版本说明与技术背景1.1 Gazebo 版本分支1.2 版本选择建议 二、系统环境准备2.1 硬件要求2.2 软件依赖 三、Gazebo Garden 安装流程3.1 添加官方软件源3.2 执行安装命令3.3 环境验证 四、Gazebo Classic 安装方法4.1 添加软件仓库4.2 安装核心组件4.3 验证安装 五、…...

ROS 快速入门教程03
8.编写Subscriber订阅者节点 8.1 创建订阅者节点 cd catkin_ws/src/ catkin_create_pkg atr_pkg rospy roscpp std_msgs ros::Subscriber sub nh.subscribe(话题名, 缓存队列长度, 回调函数) 回调函数通常在你创建订阅者时定义。一个订阅者会监听一个话题,并在有…...

在 macOS 上合并 IntelliJ IDEA 的项目窗口
在使用 IntelliJ IDEA 开发时,可能会打开多个项目窗口,这可能会导致界面变得混乱。为了提高工作效率,可以通过合并项目窗口来简化界面。本文将介绍如何在 macOS 上合并 IntelliJ IDEA 的项目窗口。 操作步骤 打开 IntelliJ IDEA: 启动你的 I…...
相关知识点)
SEO(Search Engine Optimization,搜索引擎优化)相关知识点
SEO(Search Engine Optimization)是指搜索引擎优化,是计算机领域中通过技术手段和内容策略,提升网站在搜索引擎(如Google、Bing、百度)中自然(非付费)排名的系统性方法。是一种通过优…...
)
C#森林中的兔子(力扣题目)
C#森林中的兔子(力扣题目) 题目介绍 森林中有未知数量的兔子。提问其中若干只兔子 “还有多少只兔子与你(指被提问的兔子)颜色相同?” ,将答案收集到一个整数数组 answers 中,其中 answers[i] 是第 i 只兔子的回答。 给你数组…...
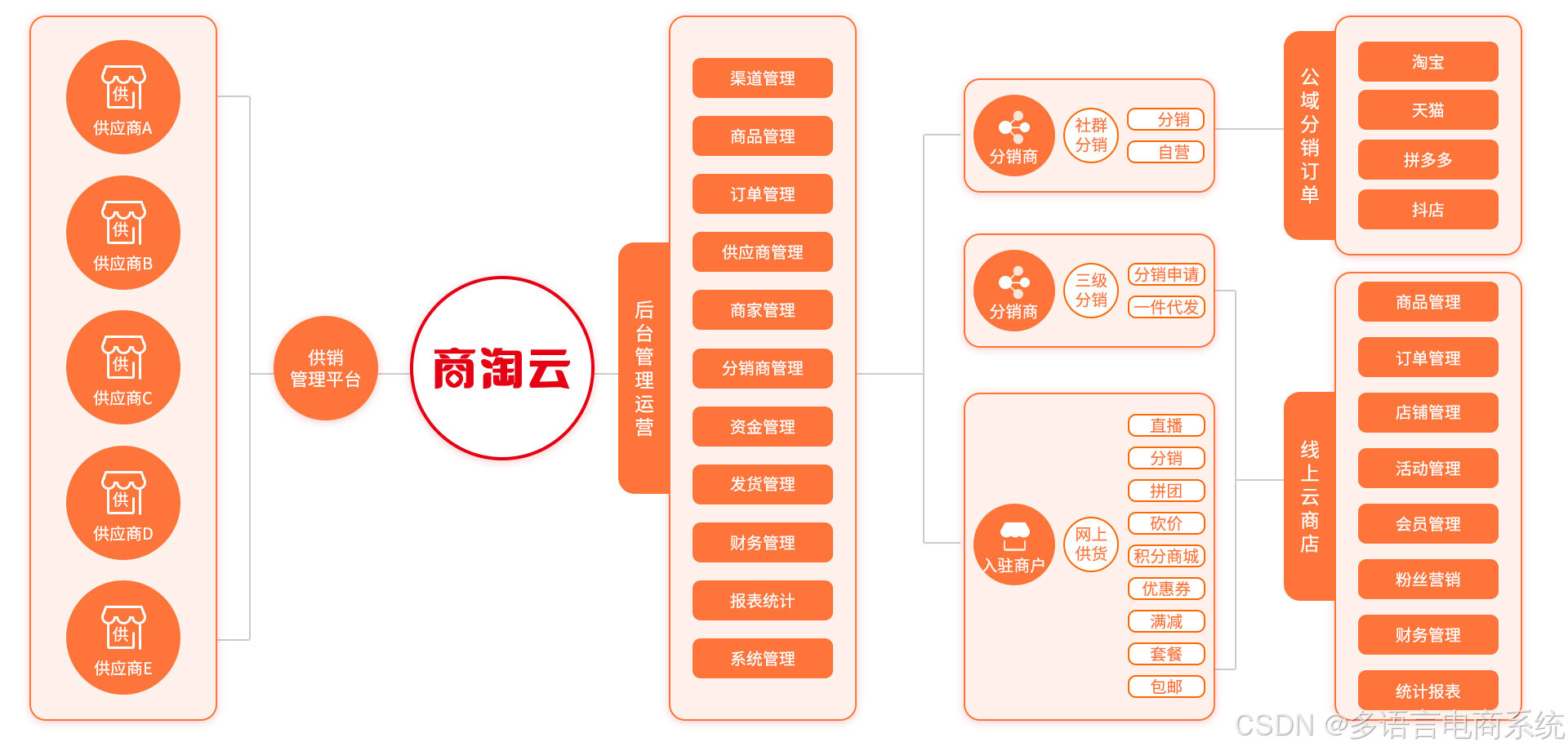
基于多用户商城系统的行业资源整合模式与商业价值探究
随着电子商务的蓬勃发展,传统的单一商家电商模式逐渐显现出一定的局限性。为了解决商家成本过高、市场竞争激烈等问题,多用户商城系统应运而生,成为一种新型的电商平台模式。通过整合行业资源,这种模式不仅极大地提升了平台和商家…...

Three.js + React 实战系列 : 从零搭建 3D 个人主页
可能你对tailiwindcss毫不了解,别紧张,记住我们只是在学习,学习的是作者的思想和技巧,并不是某一行代码。 在之前的几篇文章中,我们已经熟悉了 Three.js 的基本用法,并通过 react-three-fiber 快速构建了一…...

如何用大模型技术重塑物流供应链
摘要 在数字化转型加速的背景下,大模型技术凭借其强大的数据分析、逻辑推理和决策优化能力,正成为物流供应链领域的核心驱动力。本文深入探讨大模型如何通过需求预测、智能调度、供应链协同、风险管控等关键环节,推动物流行业从 "经验驱…...

敏捷开发管理流程
以下是敏捷开发管理流程的详细说明,包含流程框架、关键步骤及案例示例: 敏捷开发管理流程 1. 敏捷核心原则 迭代交付:分小周期(Sprint)交付可工作的软件,通常2~4周为一个迭代。用户需求驱动:以…...

【银河麒麟高级服务器操作系统】磁盘只读问题分析
系统环境及配置 系统环境 物理机/虚拟机/云/容器 虚拟机 网络环境 外网/私有网络/无网络 私有网络 硬件环境 机型 KVM Virtual Machine 处理器 Kunpeng-920 内存 32 GiB 整机类型/架构 arm64 固件版本 EFI Development Kit II / OVMF 软件环境 具体操作系统版…...

机器视觉的智能手机屏贴合应用
在智能手机制造领域,屏幕贴合工艺堪称"微米级的指尖芭蕾"。作为影响触控灵敏度、显示效果和产品可靠性的关键工序,屏幕贴合精度直接决定了用户体验。传统人工对位方式已无法满足全面屏时代对极窄边框和超高屏占比的严苛要求,而Mast…...

ETL 数据集成都包含哪些?
一、ETL 数据集成都包含哪些? 数字化时代数据已成为企业最为宝贵的资产之一。然而,企业的数据往往分散在多个不同的系统和平台中,如关系型数据库、文件系统、API 等。为了将这些分散的数据整合起来,为企业决策提供全面、准确的支…...

AIM Robotics电动胶枪:智能分配,让机器人点胶涂胶精准无误
在现代工业自动化和智能制造领域,精确的液体分配技术正成为提升生产效率和产品质量的重要因素。AIM Robotics作为这一领域的创新者,提供了多种高效、灵活的点胶涂胶分配解决方案。本文将带您了解AIM Robotics的核心技术、产品系列以及在各行业的成功应用…...

负环-P3385-P2136
通过选择标签,洛谷刷一个类型的题目还是很方便的 模版题P3385 P3385 【模板】负环 - 洛谷 Tint(input())def bellman(n,edges,sta):INFfloat(inf)d[INF]*(n1)d[sta]0for i in range(n-1):for u,v,w in edges:ncostd[u]wif ncost<d[v]:d[v]ncostfor u,v,w in e…...

抖音的逆向工程获取弹幕(websocket和protobuf解析)
目录 声明前言第一节 获取room_id和ttwid值第二节 signture值逆向python 实现signature第三节 Websocket实现长链接请求protubuf反序列化pushFrame反序列化Response解压和反序列化消息体Message解析应答ack参考博客声明 本文章中所有内容仅供学习交流使用,不用于其他任何目的…...

点云配准算法之NDT算法原理详解
一、算法概述 NDT(Normal Distributions Transform)最初用于2D激光雷达地图构建(Biber & Straer, 2003),后扩展为3D点云配准。它将点云数据空间划分为网格单元(Voxel),在每个体…...
