【差分隐私】假设检验的视角(高斯差分隐私)
在差分隐私中,假设检验的框架被用来量化攻击者通过机制输出区分两个相邻数据集 S S S 和 S ′ S' S′ 的难度。这种区分的根本困难直接反映了隐私保护强度。以下是对问题的详细解释:
1. 假设检验的基本设定
- 原假设 H 0 H_0 H0:数据集为 S S S,对应机制输出分布 P = M ( S ) P = M(S) P=M(S)。
- 备择假设 H 1 H_1 H1:数据集为 S ′ S' S′,对应机制输出分布 Q = M ( S ′ ) Q = M(S') Q=M(S′)。
- 拒绝规则 ϕ \phi ϕ:一个函数 ϕ : 输出域 → [ 0 , 1 ] \phi: \text{输出域} \to [0,1] ϕ:输出域→[0,1],表示基于机制输出结果拒绝 H 0 H_0 H0 的概率。例如:
- 若 ϕ ( 输出 ) = 1 \phi(\text{输出}) = 1 ϕ(输出)=1,则完全拒绝 H 0 H_0 H0;
- 若 ϕ ( 输出 ) = 0 \phi(\text{输出}) = 0 ϕ(输出)=0,则完全接受 H 0 H_0 H0;
- 若 ϕ ( 输出 ) = 0.7 \phi(\text{输出}) = 0.7 ϕ(输出)=0.7,则以 70% 的概率拒绝 H 0 H_0 H0。
2. 第一类错误与第二类错误的定义
-
第一类错误(Type I Error, α ϕ \alpha_\phi αϕ):
- 定义:当数据实际来自 S S S(即 H 0 H_0 H0 为真)时,错误拒绝 H 0 H_0 H0 的概率。
- 公式: α ϕ = E P [ ϕ ] = ∫ ϕ ( 输出 ) d P ( 输出 ) \alpha_\phi = \mathbb{E}_P[\phi] = \int \phi(\text{输出}) \, dP(\text{输出}) αϕ=EP[ϕ]=∫ϕ(输出)dP(输出)。
- 直观解释:攻击者在数据为 S S S 时误判为 S ′ S' S′ 的概率,对应“假阳性”。
-
第二类错误(Type II Error, β ϕ \beta_\phi βϕ):
- 定义:当数据实际来自 S ′ S' S′(即 H 1 H_1 H1 为真)时,错误接受 H 0 H_0 H0 的概率。
- 公式: β ϕ = 1 − E Q [ ϕ ] = 1 − ∫ ϕ ( 输出 ) d Q ( 输出 ) \beta_\phi = 1 - \mathbb{E}_Q[\phi] = 1 - \int \phi(\text{输出}) \, dQ(\text{输出}) βϕ=1−EQ[ϕ]=1−∫ϕ(输出)dQ(输出)。
- 直观解释:攻击者在数据为 S ′ S' S′ 时未能拒绝 H 0 H_0 H0 的概率,对应“假阴性”。
3. 错误权衡与隐私保护的关系
(1) 错误权衡曲线(ROC Curve)
攻击者需在两种错误之间权衡:降低 α ϕ \alpha_\phi αϕ(减少误判)会增加 β ϕ \beta_\phi βϕ(漏判风险),反之亦然。
- 理想情况:若 P = Q P = Q P=Q(即机制无法区分 S S S 和 S ′ S' S′),则所有 ϕ \phi ϕ 均满足 α ϕ = 1 − β ϕ \alpha_\phi = 1 - \beta_\phi αϕ=1−βϕ,即错误完全不可分。
- 实际隐私机制:差分隐私要求 P P P 和 Q Q Q 足够接近,使得任何 ϕ \phi ϕ 的 α ϕ \alpha_\phi αϕ 和 β ϕ \beta_\phi βϕ 均无法同时很小。
(2) 差分隐私的约束
对于满足 ( ϵ , 0 ) (\epsilon, 0) (ϵ,0)-差分隐私的机制 M M M,所有事件 A A A 满足:
P ( A ) ≤ e ϵ Q ( A ) 和 Q ( A ) ≤ e ϵ P ( A ) . P(A) \leq e^\epsilon Q(A) \quad \text{和} \quad Q(A) \leq e^\epsilon P(A). P(A)≤eϵQ(A)和Q(A)≤eϵP(A).
代入拒绝规则 ϕ \phi ϕ,可推导出:
α ϕ + e ϵ β ϕ ≥ 1 (约束攻击者的错误权衡) . \alpha_\phi + e^\epsilon \beta_\phi \geq 1 \quad \text{(约束攻击者的错误权衡)}. αϕ+eϵβϕ≥1(约束攻击者的错误权衡).
- 含义:当 ϵ → 0 \epsilon \to 0 ϵ→0 时, α ϕ + β ϕ ≥ 1 \alpha_\phi + \beta_\phi \geq 1 αϕ+βϕ≥1,即攻击者无法同时降低两种错误(隐私性最强);
- 当 ϵ \epsilon ϵ 增大时,约束放宽,攻击者可能找到更好的 ϕ \phi ϕ 降低错误率(隐私性减弱)。
4. 数学推导示例
以 ( ϵ , 0 ) (\epsilon, 0) (ϵ,0)-DP 为例,对任意拒绝规则 ϕ \phi ϕ,有:
E P [ ϕ ] ≤ e ϵ E Q [ ϕ ] + δ ( 当 δ = 0 时 ) . \mathbb{E}_P[\phi] \leq e^\epsilon \mathbb{E}_Q[\phi] + \delta \quad (\text{当 } \delta=0 \text{ 时}). EP[ϕ]≤eϵEQ[ϕ]+δ(当 δ=0 时).
代入 α ϕ = E P [ ϕ ] \alpha_\phi = \mathbb{E}_P[\phi] αϕ=EP[ϕ] 和 β ϕ = 1 − E Q [ ϕ ] \beta_\phi = 1 - \mathbb{E}_Q[\phi] βϕ=1−EQ[ϕ],可得:
α ϕ ≤ e ϵ ( 1 − β ϕ ) . \alpha_\phi \leq e^\epsilon (1 - \beta_\phi). αϕ≤eϵ(1−βϕ).
整理得:
α ϕ + e ϵ β ϕ ≥ 1. \alpha_\phi + e^\epsilon \beta_\phi \geq 1. αϕ+eϵβϕ≥1.
这表明攻击者的错误率必须满足此不等式,从而无法自由优化两类错误。
5. 直观解释
- 隐私保护视角:差分隐私通过限制分布 P P P 和 Q Q Q 的相似性,使得攻击者无法设计高效的拒绝规则 ϕ \phi ϕ 来显著降低错误率。
- 技术本质:无论攻击者如何选择 ϕ \phi ϕ,其区分 S S S 和 S ′ S' S′ 的能力被机制 M M M 的隐私参数 ϵ \epsilon ϵ 严格约束。
- 极端情况:
- 若 ϵ = 0 \epsilon = 0 ϵ=0,则 P = Q P = Q P=Q,此时 α ϕ + β ϕ = 1 \alpha_\phi + \beta_\phi = 1 αϕ+βϕ=1(完全无法区分);
- 若 ϵ → ∞ \epsilon \to \infty ϵ→∞,则约束消失,攻击者可能完美区分 S S S 和 S ′ S' S′。
6. 实际意义
- 评估隐私机制:通过分析最优 ϕ \phi ϕ 的错误率,可量化机制的实际隐私泄露风险。
- 设计隐私算法:在机制设计中需确保 P P P 和 Q Q Q 的相似性满足差分隐私约束,从而限制攻击者的假设检验能力。
- 与统计检验的联系:Neyman-Pearson引理指出,似然比检验是最优的,但差分隐私通过限制似然比的上界( e ϵ e^\epsilon eϵ)直接约束了检验的效力。
总结
第一类错误( α ϕ \alpha_\phi αϕ)和第二类错误( β ϕ \beta_\phi βϕ)的定义反映了攻击者通过机制输出区分相邻数据集的困难程度。差分隐私通过数学约束 P P P 和 Q Q Q 的相似性,使得攻击者无法同时降低两种错误率,从而保护个体隐私。这种错误权衡的严格约束是差分隐私理论的核心贡献之一。
相关文章:
)
【差分隐私】假设检验的视角(高斯差分隐私)
在差分隐私中,假设检验的框架被用来量化攻击者通过机制输出区分两个相邻数据集 S S S 和 S ′ S S′ 的难度。这种区分的根本困难直接反映了隐私保护强度。以下是对问题的详细解释: 1. 假设检验的基本设定 原假设 H 0 H_0 H0:数据集为 …...

计算机组成原理 课后练习
例一: 例二: 1. 原码一位乘 基本原理 原码是一种直接表示数值符号和大小的方式:最高位为符号位(0表示正,1表示负),其余位表示数值的绝对值。原码一位乘的核心思想是逐位相乘,并通…...

pytorch手动调整学习率
文章目录 1. 为什么引入学习率衰减?2. 针对不同层设置不一样的学习率3. 手动更新学习率4. 使用学习率调度器5. 推荐做法 在前面的文章中,介绍了各种学习率。在此,将进行拓展,学习如何手动更新学习率(即不使用pytorch自…...

SVN仓库突然没有权限访问
如果svn仓库突然出现无法访问的情况,提示没有权限,所有账号都是如此,新创建的账号也不行。 并且会突然提示要输入账号密码。 出现这个情况时,大概率库里面的文件有http或者https的字样,因为单独给该文件添加权限导致…...

【Qt】文件
🌈 个人主页:Zfox_ 🔥 系列专栏:Qt 目录 一:🔥 Qt 文件概述 二:🔥 输入输出设备类 三:🔥 文件读写类 四:🔥 文件和目录信息类 五&…...
)
7.DJI-PSDK:psdk负载应用固件升级(基于RTOS)
DJI-PSDK:psdk负载应用固件升级(基于RTOS): 在单片机应用程序开发阶段,我们可以借助keil5和J-LINK来直接下载应用程序进行开发和调试, 但在产品交付之后,我们对应用程序做了改动和升级,是断然不可能采用这种方式的,我们应该将新版本的程序固件打包发给客户, 能够方便用…...

ArrayUtils:数组操作的“变形金刚“——让你的数组七十二变
各位数组操控师们好!今天给大家带来的是Apache Commons Lang3中的ArrayUtils工具类。这个工具就像数组界的"孙悟空",能让你的数组随心所欲地变大、变小、变长、变短,再也不用对着原生数组的"死板"叹气了! 一…...

架构-系统可靠性分析与设计
一、可靠性相关基本概念 1. 可靠性与可用性 可靠性:软件系统在遇到错误、意外操作或系统故障时,仍能维持自身功能特性的能力。 举例:手机银行APP在用户误操作(如快速点击多次转账)时,仍能正确处理交易并避…...

【AI】[特殊字符]生产规模的向量数据库 Pinecone 使用指南
一、Pinecone 的介绍 Pinecone是一个完全托管的向量数据库服务,专为大规模机器学习应用设计。它允许开发者轻松存储、搜索和管理高维向量数据,为推荐系统、语义搜索、异常检测等应用提供强大的基础设施支持。 1.1 Pinecone的核心特性 1. 高性能向量搜…...

大模型备案对模型训练语料的要求
昨天接到一位客户的咨询,说他们的模型还在开发阶段,想提前了解一下大模型备案政策中对于模型训练语料有什么具体要求,提前规避一下。客户确实有前瞻性,考虑得比较充分。训练语料在研发阶段至关重要,直接影响模型的性能…...

dstream
DStream转换DStream 上的操作与 RDD 的类似,分为 Transformations(转换)和 Output Operations(输出)两种,此外转换操作中还有一些比较特殊的原语,如:updateStateByKey()、transform(…...

CentOS系统中MySQL安装步骤分享
在 CentOS 系统上安装 MySQL,需要依次进行环境检查、软件源配置、安装 MySQL、启动服务等操作。我将按照规范流程,为你详细分享完整且具体的安装步骤。 在 CentOS 系统中安装 MySQL 数据库,能够为各类应用提供高效稳定的数据存储和管理服务。…...
HFSS5(李明洋)——设置激励(波端口激励)
Magnetic是适用于铁磁氧导体的,只有前三种激励类型可以用于计算S参数 1波端口激励 也可以设置在模型内部,如果是设置在模型内部必须加一段理想导体,用于指定端口方向 1.1——模式 number 输入N:计算1-N的模式都计算 1.2——模式…...
ubiquant比赛系列——用docker准备ubipoker开发环境
比赛过程: 环境准备: #在云服务器上拉python官方的docker镜像并下载到本地 https://hub.docker.com/_/python/ sudo docker pull python:3.11.12-slim-bullseye sudo docker images sudo docker save -o 3.11.12-slim-bullseye.tar python:3.11.12-slim…...

运维打铁:Mysql 分区监控以及管理
文章目录 一、简介二、设计逻辑1、配置文件检查2、创建逻辑3、 删除逻辑4、重建表分区逻辑5、recognize maxvalue分区表逻辑6、创建多个未来分区逻辑7、定时检测分区是否创建成功,否则发送告警邮件。 三、解决的问题四、配置例子与介绍 一、简介 操作数据库…...

Rust实现高性能目录扫描工具ll的技术解析
Rust实现高性能目录扫描工具ll的技术解析 一、项目概述 本项目使用Rust构建了一个类ls命令行工具,具备以下核心特性: 多格式文件信息展示并行目录扫描加速人类可读文件大小运行时性能统计交互式进度提示 二、技术架构 1. 关键技术栈 clapÿ…...

深入理解C语言变量:从基础到实践
在编程世界中,变量是最基础也是最重要的概念之一。作为C语言的核心组成部分,变量承载着程序运行时数据的存储和传递功能。理解变量的工作原理和正确使用方法,是成为一名合格C程序员的必经之路。本文将全面介绍C语言变量的各个方面,…...

深入解析 SMB 相关命令:smbmap、smbclient、netexec 等工具的使用指南
Server Message Block(SMB)协议是广泛应用于文件共享、打印机共享和进程间通信的网络协议,尤其在 Windows 环境中常见。渗透测试和网络安全审计中,SMB 是一个重要的攻击面,相关工具如 smbmap、smbclient 和 netexec 提…...

RK3562/3588 系列之0—NPU基础概念
RK3562/3588 系列之0—NPU基础概念 1.处理器分类2.算力衡量指标TOPS参考文献 1.处理器分类 中央处理器(CPU); 图形处理器 (GPU); 神经网络处理器(NPU)。 每个处理器擅长不同的任务:CPU擅长顺序控制和即时性;GPU适合并行数据流处理,NPU擅长…...

springboot如何管理多数据源?
静态多数据源管理 配置多个数据源 :创建多个数据源的配置类,通常使用 @ConfigurationProperties 注解来绑定配置文件中的数据源属性,并通过 @Bean 注解定义多个 DataSource Bean 。例如: 配置类: @Configuration public class DataSourceConfig {@Bean(name = "prima…...

为什么vue的key值,不用index?
在 Vue 中,key 的作用是帮助框架高效地识别和复用 DOM 节点或组件实例。使用数组索引 (index) 作为 key 值可能会导致以下问题,因此通常不建议这样做: 1. 列表数据变化时,可能导致错误的 DOM 复用 问题:当列表的顺序…...

canvas画板!随意画!!
希望你天天开心 代码: <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>绘画板</title…...

Float32、Float16、BFloat16
我们先介绍 Float32、Float16、BFloat16 的 浮点数表示方法 然后根据浮点数表示,来分析总结他们是怎么控制 精度和 数值范围 的 最后再来对比的说明 Float32、Float16、BFloat16 的 应用场景 和 硬件支持 1、浮点数的表示方法 Float32 : 单精度浮点数…...
C# new Bitmap(32043, 32043, PixelFormat.Format32bppArgb)报错:参数无效,如何将图像分块化处理?
C#处理非常大的图像(如 32043x32043 像素)时,确实需要采取分块化处理的方法来避免内存不足的问题。分块化处理可以将大图像分割成多个较小的块,分别进行处理和保存,最后再合并这些块以形成完整的图像。以下是一个详细的…...

5V 1A充电标准的由来与技术演进——从USB诞生到智能手机时代的电力革命
点击下面图片带您领略全新的嵌入式学习路线 🔥爆款热榜 88万阅读 1.6万收藏 一、起源:USB标准与早期电力传输需求 1. USB的诞生背景 1996年,由英特尔、微软、IBM等公司组成的USB-IF(USB Implementers Forum)发布了…...

微信小程序蓝牙连接打印机打印单据完整Demo【蓝牙小票打印】
文章目录 一、准备工作1. 硬件准备2. 开发环境 二、小程序配置1. 修改app.json 三、完整代码实现1. pages/index/index.wxml2. pages/index/index.wxss3. pages/index/index.js 四、ESC/POS指令说明五、测试流程六、常见问题解决七、进一步优化建议 下面我将提供一个完整的微信…...

龙虎榜——20250425
指数依然在震荡,等待方向选择,整体量能不搞但个股红多绿少。 2025年4月25日龙虎榜行业方向分析 一、核心主线方向 绿色电力(政策驱动业绩弹性) • 代表标的:华银电力(绿电运营)、西昌电力&…...

计算机组成原理:指令系统
计算机组成原理:指令集系统 指令集体系结构(ISA)ISA定义ISA包含的内容举个栗子指令的基本组成(操作码+地址码)指令分类:地址码的个数定长操作码变长操作码变长操作码的原则变长操作码的设计指令寻址寻址方式的目的寻址方式分类有效地址直接在指令中给出有效地址间接给出有效地…...

【Go语言】RPC 使用指南(初学者版)
RPC(Remote Procedure Call,远程过程调用)是一种计算机通信协议,允许程序调用另一台计算机上的子程序,就像调用本地程序一样。Go 语言内置了 RPC 支持,下面我会详细介绍如何使用。 一、基本概念 在 Go 中&…...
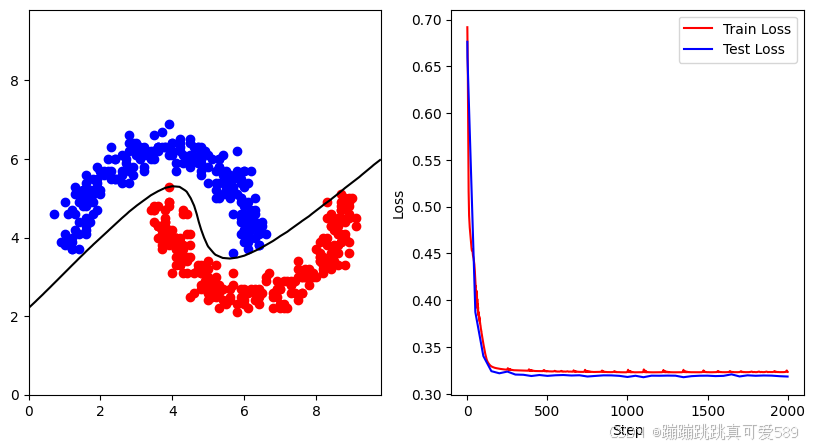
Python----深度学习(基于深度学习Pytroch簇分类,圆环分类,月牙分类)
一、引言 深度学习的重要性 深度学习是一种通过模拟人脑神经元结构来进行数据学习和模式识别的技术,在分类任务中展现出强大的能力。 分类任务的多样性 分类任务涵盖了各种场景,例如簇分类、圆环分类和月牙分类,每种任务都有不同的…...
