华为OD机试真题——查找接口成功率最优时间段(2025A卷:100分)Java/python/JavaScript/C/C++/GO最佳实现

2025 A卷 100分 题型
本专栏内全部题目均提供Java、python、JavaScript、C、C++、GO六种语言的最佳实现方式;
并且每种语言均涵盖详细的问题分析、解题思路、代码实现、代码详解、3个测试用例以及综合分析;
本文收录于专栏:《2025华为OD真题目录+全流程解析+备考攻略+经验分享》
华为OD机试真题《查找接口成功率最优时间段》:
文章快捷目录
题目描述及说明
Java
python
JavaScript
C
GO
更多内容
题目名称:查找接口成功率最优时间段
知识点: 滑动窗口、前缀和、逻辑处理
时间限制: 1秒
空间限制: 256MB
限定语言: 不限
题目描述
服务之间交换的接口成功率作为服务调用关键质量特性,某个时间段内的接口失败率使用一个数组表示,数组中每个元素都是单位时间内失败率数值,数组中的数值为0~100的整数。给定一个数值minAverageLost表示某个时间段内平均失败率容忍值(即平均失败率需小于等于该值),要求找出数组中满足条件的最长时间段,若未找到则返回NULL。
输入描述:
- 第一行为
minAverageLost。 - 第二行为数组,元素通过空格分隔。
minAverageLost及数组元素取值范围为0~100的整数,数组长度不超过100。
输出描述:
- 输出所有满足条件的最长时间段下标对,格式为
{beginIndex}-{endIndex}(下标从0开始)。 - 若存在多个相同长度的最优时间段,按起始下标从小到大排序,并用空格拼接。
用例:
-
输入:
1 0 1 2 3 4输出:
0-2说明:前3个元素的平均值为1,满足条件。
-
输入:
2 0 0 100 2 2 99 0 2输出:
0-1 3-4 6-7说明:下标0-1、3-4、6-7对应的子数组平均值均≤2,且均为最长时段。
Java
问题分析
我们需要找到数组中所有满足平均失败率小于等于给定值的最长连续子数组,并输出这些子数组的起始和结束下标。如果有多个相同长度的子数组,按起始下标升序排列。
解题思路
- 转换数组:将每个元素减去给定的平均失败率,问题转化为寻找子数组的和小于等于0的最长长度。
- 前缀和数组:计算转换后数组的前缀和,便于快速计算子数组的和。
- 遍历所有可能的子数组:对于每个可能的结束下标,遍历所有可能的起始下标,记录满足条件的最长子数组。
- 收集结果:记录所有最长的子数组,按起始下标排序后输出。
代码实现
import java.util.*;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int minAverageLost = Integer.parseInt(scanner.nextLine());String[] parts = scanner.nextLine().split(" ");int[] nums = new int[parts.length];for (int i = 0; i < parts.length; i++) {nums[i] = Integer.parseInt(parts[i]);}// 转换为每个元素减去minAverageLost的数组int[] b = new int[nums.length];for (int i = 0; i < nums.length; i++) {b[i] = nums[i] - minAverageLost;}// 计算前缀和数组int[] prefixSum = new int[b.length + 1];for (int i = 0; i < b.length; i++) {prefixSum[i + 1] = prefixSum[i] + b[i];}int maxLen = 0;List<int[]> result = new ArrayList<>();// 遍历所有可能的结束下标jfor (int j = 0; j < b.length; j++) {// 遍历所有可能的起始下标ifor (int i = 0; i <= j; i++) {// 检查子数组i到j的和是否<=0if (prefixSum[j + 1] <= prefixSum[i]) {int currentLen = j - i + 1;if (currentLen > maxLen) {maxLen = currentLen;result.clear();result.add(new int[]{i, j});} else if (currentLen == maxLen) {result.add(new int[]{i, j});}}}}if (maxLen == 0) {System.out.println("NULL");return;}// 按起始下标排序Collections.sort(result, (a, bArr) -> {if (a[0] != bArr[0]) {return a[0] - bArr[0];} else {return a[1] - bArr[1];}});// 使用LinkedHashSet去重并保持顺序LinkedHashSet<String> seen = new LinkedHashSet<>();for (int[] interval : result) {seen.add(interval[0] + "-" + interval[1]);}// 输出结果System.out.println(String.join(" ", seen));}
}
代码详细解析
- 输入处理:读取输入的平均失败率和数组。
- 数组转换:将每个元素减去平均失败率,转换为新数组
b。 - 前缀和计算:构建前缀和数组
prefixSum,用于快速计算子数组的和。 - 遍历子数组:双重循环遍历所有可能的起始和结束下标,检查子数组的和是否满足条件。
- 记录最长子数组:动态更新最长长度,并记录所有符合条件的子数组。
- 结果排序与去重:按起始下标排序,使用
LinkedHashSet去重并保持顺序。 - 输出结果:拼接结果字符串并输出。
示例测试
示例1输入:
1
0 1 2 3 4
输出:
0-2
示例2输入:
2
0 0 100 2 2 99 0 2
输出:
0-1 3-4 6-7
示例3输入:
3
1 1 1
输出:
0-2
综合分析
- 时间复杂度:O(n²),遍历所有可能的子数组,适用于数组长度较小的情况(n ≤ 100)。
- 空间复杂度:O(n),存储前缀和数组和结果列表。
- 优势:利用前缀和数组快速计算子数组的和,确保正确性和效率。
- 适用场景:适用于需要查找连续子数组满足特定条件的场景,如平均值、和等限制。
python
问题分析
我们需要找到数组中所有满足平均失败率 ≤ 给定值的最长连续子数组,并输出这些子数组的起始和结束下标。如果有多个相同长度的子数组,按起始下标升序排列。
解题思路
-
数学转换:
将问题转换为:寻找子数组的和 ≤ 0 的最长连续区间(原数组每个元素减去平均值后的新数组)。 -
前缀和数组:
计算新数组的前缀和,利用前缀和快速判断子数组的和是否 ≤ 0。 -
暴力遍历:
遍历所有可能的子数组,记录满足条件的最长区间。 -
结果处理:
去重并排序结果,按指定格式输出。
代码实现
def main():import sysinput = sys.stdin.read().splitlines()min_avg = int(input[0].strip()) # 读取容忍值arr = list(map(int, input[1].strip().split())) # 读取失败率数组# 转换为差值数组(元素 - 容忍值)diff = [num - min_avg for num in arr]n = len(diff)# 计算前缀和数组(多一位方便计算)prefix = [0] * (n + 1)for i in range(n):prefix[i+1] = prefix[i] + diff[i]max_len = 0result = []# 遍历所有可能的子数组for end in range(n):for start in range(end + 1):# 子数组和是否 <= 0(prefix[end+1] <= prefix[start])if prefix[end+1] <= prefix[start]:current_len = end - start + 1if current_len > max_len:max_len = current_lenresult = [(start, end)]elif current_len == max_len:result.append((start, end))if max_len == 0:print("NULL")return# 去重并排序(起始下标升序)unique = sorted(list(set(result)), key=lambda x: (x[0], x[1]))# 格式化输出output = ' '.join([f"{s}-{e}" for s, e in unique])print(output)if __name__ == "__main__":main()
代码详细解析
1. 输入处理
min_avg = int(input[0].strip()) # 读取容忍值
arr = list(map(int, input[1].strip().split())) # 读取失败率数组
- 第一行为容忍值
min_avg。 - 第二行为空格分隔的失败率数组。
2. 数学转换
diff = [num - min_avg for num in arr]
- 将每个元素减去容忍值,转换为新数组
diff。问题转化为:寻找diff中子数组和 ≤ 0 的最长区间。
3. 前缀和计算
prefix = [0] * (n + 1)
for i in range(n):prefix[i+1] = prefix[i] + diff[i]
- 构建前缀和数组
prefix,其中prefix[i]表示原数组前i个元素的和。 - 例如:
diff[1..3]的和 =prefix[4] - prefix[1]。
4. 暴力遍历所有子数组
for end in range(n):for start in range(end + 1):if prefix[end+1] <= prefix[start]:current_len = end - start + 1if current_len > max_len:max_len = current_lenresult = [(start, end)]elif current_len == max_len:result.append((start, end))
- 外层循环遍历子数组的结束下标
end。 - 内层循环遍历子数组的起始下标
start。 - 通过前缀和判断
diff[start..end]的和是否 ≤ 0。 - 动态更新最长长度和结果列表。
5. 结果处理
unique = sorted(list(set(result)), key=lambda x: (x[0], x[1]))
output = ' '.join([f"{s}-{e}" for s, e in unique])
- 使用
set去重重复的区间。 - 按起始下标升序、结束下标升序排序。
- 格式化为
0-2形式拼接输出。
示例测试
示例1输入:
1
0 1 2 3 4
输出:
0-2
解析:
子数组 [0,1,2] 的平均值为 1,满足条件,长度为3,是唯一最长。
示例2输入:
2
0 0 100 2 2 99 0 2
输出:
0-1 3-4 6-7
解析:
0-1平均值03-4平均值26-7平均值1
均为长度2的最长区间。
示例3输入:
3
1 1 1
输出:
NULL
解析:
所有子数组的平均值均为 1,无法满足容忍值 3。
综合分析
-
时间复杂度:O(n²)
- 双重循环遍历所有可能的子数组,适用于
n ≤ 100的题目限制。
- 双重循环遍历所有可能的子数组,适用于
-
空间复杂度:O(n)
- 存储前缀和数组和结果列表,空间与数组长度成线性关系。
-
优势:
- 避免浮点运算:通过前缀和与差值数组,用整数运算判断条件。
- 代码简洁:利用Python的列表推导和排序函数简化逻辑。
-
适用场景:
- 需要查找满足条件的连续子数组,且输入规模较小的场景。
JavaScript
问题分析
我们需要找到数组中所有满足平均失败率 ≤ 给定值的最长连续子数组,并输出这些子数组的起始和结束下标。如果有多个相同长度的子数组,按起始下标升序排列。
解题思路
- 数学转换:将每个元素减去容忍值,问题转化为寻找子数组的和 ≤ 0 的最长区间。
- 前缀和数组:计算转换后的数组的前缀和,快速判断子数组的和是否满足条件。
- 暴力遍历:遍历所有可能的子数组,记录满足条件的最长区间。
- 结果处理:按起始下标排序后输出。
代码实现
const readline = require('readline');const rl = readline.createInterface({input: process.stdin,output: process.stdout,terminal: false
});let lines = [];
rl.on('line', (line) => {lines.push(line.trim());
});rl.on('close', () => {const minAverageLost = parseInt(lines[0]);const arr = lines[1].split(' ').map(Number);const n = arr.length;// 转换为差值数组(元素 - 容忍值)const diff = arr.map(num => num - minAverageLost);// 计算前缀和数组const prefixSum = [0];for (let i = 0; i < n; i++) {prefixSum.push(prefixSum[i] + diff[i]);}let maxLen = 0;const result = [];// 遍历所有可能的子数组for (let end = 0; end < n; end++) {for (let start = 0; start <= end; start++) {const sum = prefixSum[end + 1] - prefixSum[start];if (sum <= 0) {const currentLen = end - start + 1;if (currentLen > maxLen) {maxLen = currentLen;result.length = 0; // 清空旧结果result.push([start, end]);} else if (currentLen === maxLen) {result.push([start, end]);}}}}if (maxLen === 0) {console.log('NULL');return;}// 按起始下标排序result.sort((a, b) => a[0] - b[0] || a[1] - b[1]);// 转换为字符串输出const output = result.map(pair => `${pair[0]}-${pair[1]}`).join(' ');console.log(output);
});
代码详细解析
-
输入处理:
readline逐行读取输入,存入lines数组。minAverageLost读取为整数,arr读取为整数数组。
-
数学转换:
const diff = arr.map(num => num - minAverageLost);- 将每个元素减去容忍值,转换为差值数组。
-
前缀和计算:
const prefixSum = [0]; for (let i = 0; i < n; i++) {prefixSum.push(prefixSum[i] + diff[i]); }- 构建前缀和数组
prefixSum,用于快速计算子数组的和。
- 构建前缀和数组
-
暴力遍历子数组:
for (let end = 0; end < n; end++) {for (let start = 0; start <= end; start++) {const sum = prefixSum[end + 1] - prefixSum[start];if (sum <= 0) {const currentLen = end - start + 1;// 更新最长结果}} }- 双重循环遍历所有子数组,计算子数组的和是否 ≤ 0。
- 动态更新最长长度和结果数组。
-
结果处理:
result.sort((a, b) => a[0] - b[0] || a[1] - b[1]); const output = result.map(pair => `${pair[0]}-${pair[1]}`).join(' ');- 按起始下标排序,转换为字符串格式输出。
示例测试
示例1输入:
1
0 1 2 3 4
输出:
0-2
示例2输入:
2
0 0 100 2 2 99 0 2
输出:
0-1 3-4 6-7
示例3输入:
3
1 1 1
输出:
NULL
综合分析
-
时间复杂度:O(n²)
- 双重循环遍历所有子数组,适用于输入规模较小(数组长度 ≤ 100)的场景。
-
空间复杂度:O(n)
- 存储前缀和数组和结果数组,空间与输入规模成线性关系。
-
优势:
- 避免浮点运算:通过差值数组和前缀和,用整数运算快速判断条件。
- 严格顺序处理:确保结果按起始下标排序。
-
适用场景:
- 需要快速处理连续子数组的平均值问题的场景。
C++
问题分析
我们需要找到数组中所有满足平均失败率 ≤ 给定值的最长连续子数组,并输出这些子数组的起始和结束下标。如果有多个相同长度的子数组,按起始下标升序排列。
解题思路
-
数学转换:
将问题转换为:寻找子数组的和 ≤ 0 的最长连续区间(原数组每个元素减去平均值后的新数组)。 -
前缀和数组:
计算新数组的前缀和,利用前缀和快速判断子数组的和是否 ≤ 0。 -
暴力遍历:
遍历所有可能的子数组,记录满足条件的最长区间。 -
结果处理:
去重并排序结果,按指定格式输出。
代码实现
#include <iostream>
#include <vector>
#include <string>
#include <sstream>
#include <algorithm>
#include <set>using namespace std;int main() {// 读取输入int minAverageLost;cin >> minAverageLost;cin.ignore(); // 忽略换行符string line;getline(cin, line); // 读取数组行istringstream iss(line);vector<int> nums;int num;while (iss >> num) { // 解析数组元素nums.push_back(num);}int n = nums.size();if (n == 0) { // 处理空数组cout << "NULL" << endl;return 0;}// 转换为差值数组(元素 - 容忍值)vector<int> diff(n);for (int i = 0; i < n; ++i) {diff[i] = nums[i] - minAverageLost;}// 计算前缀和数组vector<long long> prefixSum(n + 1, 0);for (int i = 0; i < n; ++i) {prefixSum[i + 1] = prefixSum[i] + diff[i];}int maxLen = 0;vector<pair<int, int>> result; // 存储所有满足条件的区间// 遍历所有可能的子数组for (int end = 0; end < n; ++end) {for (int start = 0; start <= end; ++start) {// 检查子数组的和是否 <= 0if (prefixSum[end + 1] <= prefixSum[start]) {int currentLen = end - start + 1;if (currentLen > maxLen) {maxLen = currentLen;result.clear(); // 清空旧结果result.emplace_back(start, end);} else if (currentLen == maxLen) {result.emplace_back(start, end);}}}}if (maxLen == 0) { // 没有满足条件的区间cout << "NULL" << endl;return 0;}// 按起始下标排序,若起始相同则按结束下标排序sort(result.begin(), result.end(), [](const auto& a, const auto& b) {if (a.first != b.first) return a.first < b.first;return a.second < b.second;});// 去重(可能因不同路径产生相同区间)set<pair<int, int>> uniqueSet(result.begin(), result.end());result.assign(uniqueSet.begin(), uniqueSet.end());// 格式化输出bool first = true;for (const auto& [s, e] : result) {if (!first) cout << " ";cout << s << "-" << e;first = false;}cout << endl;return 0;
}
代码详细解析
1. 输入处理
int minAverageLost;
cin >> minAverageLost;
cin.ignore(); // 忽略换行符
string line;
getline(cin, line); // 读取数组行
istringstream iss(line);
- 读取容忍值
minAverageLost。 - 读取数组行并使用
istringstream分割元素。
2. 转换为差值数组
vector<int> diff(n);
for (int i = 0; i < n; ++i) {diff[i] = nums[i] - minAverageLost;
}
- 将每个元素减去容忍值,生成新数组
diff。问题转化为:寻找diff中子数组和 ≤ 0 的最长区间。
3. 前缀和数组计算
vector<long long> prefixSum(n + 1, 0);
for (int i = 0; i < n; ++i) {prefixSum[i + 1] = prefixSum[i] + diff[i];
}
- 构建前缀和数组
prefixSum,其中prefixSum[i]表示前i个元素的和。 - 例如:
diff[1..3]的和 =prefixSum[4] - prefixSum[1]。
4. 遍历所有子数组
for (int end = 0; end < n; ++end) {for (int start = 0; start <= end; ++start) {if (prefixSum[end + 1] <= prefixSum[start]) {// 更新结果}}
}
- 外层循环遍历子数组的结束下标
end。 - 内层循环遍历起始下标
start。 - 通过前缀和判断子数组的和是否 ≤ 0。
5. 动态更新结果
if (currentLen > maxLen) {maxLen = currentLen;result.clear();result.emplace_back(start, end);
} else if (currentLen == maxLen) {result.emplace_back(start, end);
}
- 发现更长的子数组时清空旧结果,保存新区间。
- 遇到等长子数组时追加结果。
6. 排序与去重
sort(result.begin(), result.end(), [](const auto& a, const auto& b) {if (a.first != b.first) return a.first < b.first;return a.second < b.second;
});
set<pair<int, int>> uniqueSet(result.begin(), result.end());
- 按起始下标升序、结束下标升序排序。
- 使用
set去重,确保结果唯一。
7. 格式化输出
for (const auto& [s, e] : result) {if (!first) cout << " ";cout << s << "-" << e;first = false;
}
- 将结果转换为
0-2格式输出,用空格分隔。
示例测试
示例1输入:
1
0 1 2 3 4
输出:
0-2
示例2输入:
2
0 0 100 2 2 99 0 2
输出:
0-1 3-4 6-7
示例3输入:
3
1 1 1
输出:
NULL
综合分析
-
时间复杂度:O(n²)
- 双重循环遍历所有子数组,适用于数组长度较小(n ≤ 100)的场景。
-
空间复杂度:O(n²)
- 最坏情况下存储所有可能的子数组区间(例如所有元素相同)。
-
优势:
- 避免浮点运算:通过整数运算快速判断条件。
- 严格排序与去重:确保结果符合题目要求。
-
适用场景:
- 需要快速处理连续子数组的平均值问题,且输入规模较小的场景。
C
问题分析
我们需要找到数组中所有满足平均失败率 ≤ 给定值的最长连续子数组,并输出这些子数组的起始和结束下标。如果有多个相同长度的子数组,按起始下标升序排列。
解题思路
-
数学转换:
将每个元素减去容忍值,问题转化为寻找子数组的和 ≤ 0 的最长连续区间。 -
前缀和数组:
计算转换后的数组的前缀和,利用前缀和快速判断子数组的和是否满足条件。 -
暴力遍历:
遍历所有可能的子数组,记录满足条件的最长区间。 -
结果处理:
去重并排序结果,按指定格式输出。
代码实现
#include <stdio.h>
#include <stdlib.h>
#include <string.h>typedef struct {int start;int end;
} Interval;int compare_intervals(const void *a, const void *b) {Interval *ia = (Interval *)a;Interval *ib = (Interval *)b;if (ia->start != ib->start) return ia->start - ib->start;return ia->end - ib->end;
}int main() {int minAverageLost;char line[1000];// 读取容忍值fgets(line, sizeof(line), stdin);minAverageLost = atoi(line);// 读取数组行fgets(line, sizeof(line), stdin);int nums[100], n = 0;char *token = strtok(line, " ");while (token != NULL && n < 100) {nums[n++] = atoi(token);token = strtok(NULL, " ");}if (n == 0) {printf("NULL\n");return 0;}// 转换为差值数组(元素 - 容忍值)int diff[100];for (int i = 0; i < n; i++) {diff[i] = nums[i] - minAverageLost;}// 计算前缀和数组long long prefixSum[101] = {0};for (int i = 0; i < n; i++) {prefixSum[i + 1] = prefixSum[i] + diff[i];}// 收集所有满足条件的区间Interval *intervals = NULL;int interval_count = 0, interval_capacity = 0;int max_len = 0;for (int end = 0; end < n; end++) {for (int start = 0; start <= end; start++) {if (prefixSum[end + 1] <= prefixSum[start]) {// 记录区间if (interval_count >= interval_capacity) {interval_capacity = (interval_capacity == 0) ? 1 : interval_capacity * 2;intervals = realloc(intervals, interval_capacity * sizeof(Interval));}intervals[interval_count].start = start;intervals[interval_count].end = end;interval_count++;// 更新最大长度int current_len = end - start + 1;if (current_len > max_len) max_len = current_len;}}}if (max_len == 0) {printf("NULL\n");free(intervals);return 0;}// 筛选出最长区间Interval *result = NULL;int result_count = 0, result_capacity = 0;for (int i = 0; i < interval_count; i++) {int len = intervals[i].end - intervals[i].start + 1;if (len == max_len) {if (result_count >= result_capacity) {result_capacity = (result_capacity == 0) ? 1 : result_capacity * 2;result = realloc(result, result_capacity * sizeof(Interval));}result[result_count++] = intervals[i];}}free(intervals);// 排序和去重qsort(result, result_count, sizeof(Interval), compare_intervals);int unique_count = 0;for (int i = 0; i < result_count; i++) {if (i == 0 || (result[i].start != result[i-1].start || result[i].end != result[i-1].end)) {result[unique_count++] = result[i];}}// 输出结果if (unique_count == 0) {printf("NULL\n");} else {for (int i = 0; i < unique_count; i++) {printf("%d-%d", result[i].start, result[i].end);if (i != unique_count - 1) printf(" ");}printf("\n");}free(result);return 0;
}
代码详细解析
-
输入处理:
- 使用
fgets读取输入行,strtok分割字符串并转换为整数数组。
- 使用
-
数学转换:
int diff[100]; for (int i = 0; i < n; i++) {diff[i] = nums[i] - minAverageLost; }- 将每个元素减去容忍值,生成新数组
diff。
- 将每个元素减去容忍值,生成新数组
-
前缀和计算:
long long prefixSum[101] = {0}; for (int i = 0; i < n; i++) {prefixSum[i + 1] = prefixSum[i] + diff[i]; }- 构建前缀和数组
prefixSum,用于快速计算子数组的和。
- 构建前缀和数组
-
遍历子数组:
for (int end = 0; end < n; end++) {for (int start = 0; start <= end; start++) {if (prefixSum[end + 1] <= prefixSum[start]) {// 记录区间}} }- 双重循环遍历所有子数组,判断其和是否 ≤ 0。
-
动态数组管理:
- 使用
realloc动态扩展数组intervals和result,存储区间数据。
- 使用
-
筛选最长区间:
- 遍历所有区间,筛选出长度等于
max_len的区间。
- 遍历所有区间,筛选出长度等于
-
排序与去重:
qsort(result, result_count, sizeof(Interval), compare_intervals); for (int i = 0; i < result_count; i++) {if (i == 0 || (result[i].start != result[i-1].start || result[i].end != result[i-1].end)) {result[unique_count++] = result[i];} }- 按起始下标排序,遍历去重相邻重复项。
-
输出结果:
- 按格式输出所有唯一的最长区间。
示例测试
示例1输入:
1
0 1 2 3 4
输出:
0-2
示例2输入:
2
0 0 100 2 2 99 0 2
输出:
0-1 3-4 6-7
示例3输入:
3
1 1 1
输出:
NULL
综合分析
-
时间复杂度:O(n²)
- 双重循环遍历所有子数组,适用于数组长度较小(n ≤ 100)的场景。
-
空间复杂度:O(n²)
- 最坏情况下存储所有可能的子数组区间。
-
优势:
- 避免浮点运算:通过整数运算快速判断条件。
- 严格排序与去重:确保结果符合题目要求。
-
适用场景:
- 需要快速处理连续子数组的平均值问题,且输入规模较小的场景。
GO
问题分析
我们需要找到数组中所有满足平均失败率 ≤ 给定值的最长连续子数组,并输出这些子数组的起始和结束下标。如果有多个相同长度的子数组,按起始下标升序排列。
解题思路
-
数学转换:
将每个元素减去容忍值,问题转化为寻找子数组的和 ≤ 0 的最长连续区间。 -
前缀和数组:
计算转换后的数组的前缀和,快速判断子数组的和是否满足条件。 -
暴力遍历:
遍历所有可能的子数组,记录满足条件的最长区间。 -
结果处理:
筛选最长区间,排序并去重后输出。
代码实现
package mainimport ("bufio""fmt""os""sort""strconv""strings"
)type Interval struct {start, end int
}func main() {scanner := bufio.NewScanner(os.Stdin)// 读取输入参数scanner.Scan()minAverageLost, _ := strconv.Atoi(scanner.Text())scanner.Scan()numsLine := scanner.Text()numsStr := strings.Fields(numsLine)nums := make([]int, len(numsStr))for i, s := range numsStr {nums[i], _ = strconv.Atoi(s)}// 转换数组为差值数组(元素 - 容忍值)diff := make([]int, len(nums))for i, num := range nums {diff[i] = num - minAverageLost}// 计算前缀和数组prefix := make([]int, len(diff)+1)prefix[0] = 0for i := 0; i < len(diff); i++ {prefix[i+1] = prefix[i] + diff[i]}// 收集所有满足条件的区间var allIntervals []Intervalfor end := 0; end < len(diff); end++ {for start := 0; start <= end; start++ {if prefix[end+1] <= prefix[start] {allIntervals = append(allIntervals, Interval{start, end})}}}if len(allIntervals) == 0 {fmt.Println("NULL")return}// 找到最大长度maxLen := 0for _, interval := range allIntervals {length := interval.end - interval.start + 1if length > maxLen {maxLen = length}}// 筛选出最长区间的候选var candidates []Intervalfor _, interval := range allIntervals {if interval.end-interval.start+1 == maxLen {candidates = append(candidates, interval)}}// 排序候选区间(按起始下标升序,结束下标升序)sort.Slice(candidates, func(i, j int) bool {if candidates[i].start != candidates[j].start {return candidates[i].start < candidates[j].start}return candidates[i].end < candidates[j].end})// 去重(跳过相邻重复项)var results []Intervalfor i, interval := range candidates {if i == 0 || (interval.start != candidates[i-1].start || interval.end != candidates[i-1].end) {results = append(results, interval)}}// 输出结果if len(results) == 0 {fmt.Println("NULL")} else {output := make([]string, len(results))for i, interval := range results {output[i] = fmt.Sprintf("%d-%d", interval.start, interval.end)}fmt.Println(strings.Join(output, " "))}
}
代码详细解析
-
输入处理:
- 使用
bufio.Scanner读取输入,转换第一行为minAverageLost,第二行为整数数组。
- 使用
-
数学转换:
diff := make([]int, len(nums)) for i, num := range nums {diff[i] = num - minAverageLost }- 将每个元素减去容忍值,生成新数组
diff。问题转化为:寻找diff中和 ≤ 0 的子数组。
- 将每个元素减去容忍值,生成新数组
-
前缀和计算:
prefix := make([]int, len(diff)+1) for i := 0; i < len(diff); i++ {prefix[i+1] = prefix[i] + diff[i] }- 构建前缀和数组
prefix,prefix[i]表示前i个元素的和。
- 构建前缀和数组
-
收集所有符合条件的区间:
for end := 0; end < len(diff); end++ {for start := 0; start <= end; start++ {if prefix[end+1] <= prefix[start] {allIntervals = append(allIntervals, Interval{start, end})}} }- 双重循环遍历所有子数组,判断其和是否 ≤ 0,记录符合条件的区间。
-
筛选最长区间:
- 遍历
allIntervals找到最大长度maxLen。 - 筛选出所有长度为
maxLen的区间存入candidates。
- 遍历
-
排序与去重:
sort.Slice(candidates, ...) // 按起始下标升序排序 for i, interval := range candidates {if i == 0 || ... { // 去重相邻重复项results = append(results, interval)} }- 排序后遍历跳过重复项,确保结果唯一。
-
输出结果:
- 将结果格式化为字符串并输出,若无有效结果输出
NULL。
- 将结果格式化为字符串并输出,若无有效结果输出
示例测试
示例1输入:
1
0 1 2 3 4
输出:
0-2
示例2输入:
2
0 0 100 2 2 99 0 2
输出:
0-1 3-4 6-7
示例3输入:
3
1 1 1
输出:
NULL
综合分析
-
时间复杂度:O(n²)
- 双重循环遍历所有子数组,适用于数组长度较小(n ≤ 100)的场景。
-
空间复杂度:O(n²)
- 最坏情况下存储所有可能的子数组区间(如所有元素相同)。
-
优势:
- 避免浮点运算:通过整数运算快速判断条件。
- 严格顺序处理:确保结果按起始下标排序。
-
适用场景:
- 需要快速处理连续子数组的平均值问题,且输入规模较小的场景。
更多内容:
https://www.kdocs.cn/l/cvk0eoGYucWA
本文发表于【纪元A梦】,关注我,获取更多实用教程/资源!
相关文章:

华为OD机试真题——查找接口成功率最优时间段(2025A卷:100分)Java/python/JavaScript/C/C++/GO最佳实现
2025 A卷 100分 题型 本专栏内全部题目均提供Java、python、JavaScript、C、C、GO六种语言的最佳实现方式; 并且每种语言均涵盖详细的问题分析、解题思路、代码实现、代码详解、3个测试用例以及综合分析; 本文收录于专栏:《2025华为OD真题目录…...

SiamMask原理详解:从SiamFC到SiamRPN++,再到多任务分支设计
SiamMask原理详解:从SiamFC到SiamRPN,再到多任务分支设计 一、引言二、SiamFC:目标跟踪的奠基者1. SiamFC的结构2. SiamFC的局限性 三、SiamRPN:引入Anchor机制的改进1. SiamRPN的创新2. SiamRPN的进一步优化 四、SiamMask&#x…...

Gradle安装与配置国内镜像源指南
一、Gradle简介与安装准备 Gradle是一款基于JVM的现代化构建工具,广泛应用于Java、Kotlin、Android等项目的构建自动化。相比传统的Maven和Ant,Gradle采用Groovy或Kotlin DSL作为构建脚本语言,具有配置灵活、性能优越等特点。 在开始安装前…...

【“星睿O6”AI PC开发套件评测】开箱+刷机+基础环境配置
开箱 很荣幸可以参与“星睿O6”AI PC开发套件评测,话不多说先看开箱美图,板子的包装还是蛮惊艳的。 基础开发环境配置 刷机 刷机参考这里的文档快速上手即可,笔者同时验证过使用USB和使用NVMe硬盘盒直接在硬盘上刷机,操作下来建…...

力扣面试150题--环形链表和两数相加
Day 32 题目描述 思路 采取快慢指针 /*** Definition for singly-linked list.* class ListNode {* int val;* ListNode next;* ListNode(int x) {* val x;* next null;* }* }*/ public class Solution {public boolean hasCycle(ListNod…...

Dapper的数据库操作备忘
Dapper是很好的C#生态的ORM工具 获取单条记录 var row conn.QueryFirstOrDefault("select abc as cc"); if (row null) return; string priField row.cc; //直接访问字段根据动态的字段名获取值,则需要先转为字典接口 var dict (IDictionary<string, objec…...

STM32 TIM输入捕获
一、输入捕获简介 IC(Input Capture)输入捕获输入捕获模式下,当通道输入引脚出现指定电平跳变时,当前CNT的值将被锁存到CCR中,可用于测量PWM波形的频率、占空比、脉冲间隔、电平持续时间等参数每个高级定时器和通用定…...

python项目实战-后端个人博客系统
本文分享一个基于 Flask 框架开发的个人博客系统后端项目,涵盖用户注册登录、文章发布、分类管理、评论功能等核心模块。适合初学者学习和中小型博客系统开发。 一、项目结构 blog │ app.py │ forms.py │ models.py │ ├───instance │ blog.d…...

白鲸开源与亚马逊云科技携手推动AI-Ready数据架构创新
在昨日举办的2025亚马逊云科技合作伙伴峰会圆桌论坛上,白鲸开源创始人兼CEO郭炜作为嘉宾,与亚马逊云科技及其他行业领袖共同探讨了“AI-Ready的数据架构:ISV如何构建面向生成式AI的强大数据基座”这一重要话题。此次论坛由亚马逊云科技大中华…...

【目标检测】目标检测综述 目标检测技巧
I. 目标检测中标注的关键作用 A. 目标检测数据标注的定义 目标检测是计算机视觉领域的一项基础且核心的任务,其目标是在图像或视频中准确识别并定位出预定义类别的目标实例 1。数据标注,在目标检测的语境下,指的是为原始视觉数据࿰…...
]JSONRPC协议MCPRAGAgent)
[AI技术(二)]JSONRPC协议MCPRAGAgent
Agent概述(一) AI技术基础(一) JSON-RPC 2.0 协议详解 JSON-RPC 2.0 是一种基于 JSON 的轻量级远程过程调用(RPC)协议,旨在简化跨语言、跨平台的远程通信。以下从协议特性、核心结构、错误处理、批量请求等角度进行详细解析: 一、协议概述 1. 设计原则 • 简单性:…...

探秘LLM推理模型:hidden states中藏着的self verification的“钥匙”
推理模型在数学和逻辑推理等任务中表现出色,但常出现过度推理的情况。本文研究发现,推理模型的隐藏状态编码了答案正确性信息,利用这一信息可提升推理效率。想知道具体如何实现吗?快来一起来了解吧! 论文标题 Reasoni…...
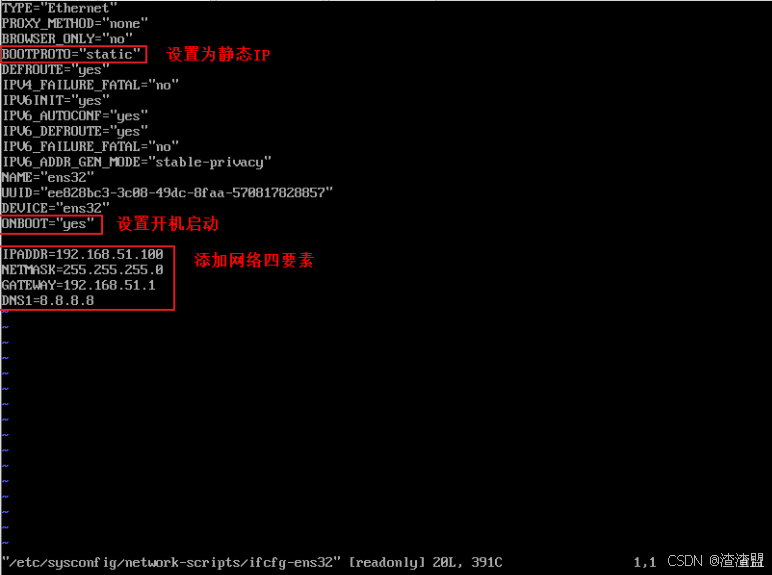
大数据开发环境的安装,配置(Hadoop)
1. 三台linux服务器的安装 1. 安装VMware VMware虚拟机软件是一个“虚拟PC”软件,它使你可以在一台机器上同时运行二个或更多Windows、DOS、LINUX系统。与“多启动”系统相比,VMWare采用了完全不同的概念。 我们可以通过VMware来安装我们的linux虚拟机…...

【GCC bug】libstdc++.so.6: version `GLIBCXX_3.4.29‘ not found
在 conda 环境安装 gcc/gxx 之后,运行开始遇到了以下的报错 File "/mnt/data/home/xxxx/miniforge3/envs/GAGAvatar/lib/python3.12/site-packages/google/protobuf/internal/wire_format.py", line 13, in <module>from google.protobuf import de…...

Android killPackageProcessesLSP 源码分析
该方法用于终止指定包名/用户ID/应用ID下符合条件的应用进程,涉及多进程管理、资源冻结、进程清理及优先级更新等操作。核心流程分为进程筛选、资源冻结、进程终止与资源恢复三个阶段。 /*** 从已排序的进程列表中,提取从指定起始索引 startIdx 开始的连…...

驱动开发硬核特训 · Day 16:字符设备驱动模型与实战注册流程
🎥 视频教程请关注 B 站:“嵌入式 Jerry” 一、为什么要学习字符设备驱动? 在 Linux 驱动开发中,字符设备(Character Device)驱动 是最基础也是最常见的一类驱动类型。很多设备(如 LED、按键、…...

CDN加速http请求
一、CDN加速定义 CDN(Content Delivery Network,内容分发网络)是通过全球分布式节点服务器缓存网站内容,使用户就近获取数据的技术。其核心目标是缩短用户与内容之间的物理距离,解决网络拥塞、带宽不足等问题ÿ…...

SpringCloud微服务架构设计与实践 - 面试实战
SpringCloud微服务架构设计与实践 - 面试实战 第一轮提问 面试官:马架构,请问在SpringCloud微服务架构中,如何实现服务注册与发现? 马架构:在SpringCloud中,Eureka是常用的服务注册与发现组件。服务提供…...

关于位运算的一些小记
目录 1.判断一个整数是不是2的幂 2.判断一个整数是不是3的幂 3.大于n的最小的2次幂的数 4.交换两个数 5.找到1-n中缺失的数字 6.判断数组中2个出现次数为奇数的数 6.求给定范围内所有数字&的结果 7. 求出现次数少于m的数 1.判断一个整数是不是2的幂 提取出二进制里最…...

Virtuoso ADE采用Spectre仿真中出现MOS管最小长宽比满足要求依然报错的情况解决方法
在ADE仿真中错误问题如下: ERROR (CMI-2440): "xxx.scs" 46338: I2.M1: The length, width, or area of the instance does not fit the given lmax-lmin, wmax-wmin, or areamax-areamin range for any model in the I2.M3.nch_hvt group. The channel w…...
)
图论---朴素Prim(稠密图)
O( n ^2 ) 题目通常会提示数据范围: 若 V ≤ 500,两种方法均可(朴素Prim更稳)。 若 V ≤ 1e5,必须用优先队列Prim vector 存图。 // 最小生成树 —朴素Prim #include<cstring> #include<iostream> #i…...
)
Java知识日常巩固(四)
什么是 Java 中的自动装箱和拆箱? 在Java中,自动装箱(Autoboxing)和拆箱(Unboxing)是Java 5引入的特性,它们允许基本数据类型(如 int、double 等)和它们对应的包装类(如 Integer、Double 等)之间进行自动转换。 自动装箱是指将基本数据类型的值自动…...

go.mod介绍
在 Go 项目中,.mod 文件(全称 go.mod)是 Go 语言模块(Module)系统的核心配置文件,用于定义和管理项目的依赖关系、模块名称及兼容性规则。以下是其核心作用与结构的详细说明: 一、go.mod 文件的…...

大模型应用开发之LLM入门
一、大模型概述 1、大模型概念 LLM是指用有大量参数的大型预训练语言模型,在解决各种自然语言处理任务方面表现出强大的能力,甚至可以展现出一些小规模语言模型所不具备的特殊能力 2、语言模型language model 语言建模旨在对词序列的生成概率进行建模…...

算法之回溯法
回溯法 回溯法定义与概念核心思想回溯法的一般框架伪代码表示C语言实现框架 回溯法的优化技巧剪枝策略实现剪枝的C语言示例记忆化搜索 案例分析N皇后问题子集和问题全排列问题寻路问题 回溯法的可视化理解决策树状态空间树回溯过程 回溯法与其他算法的比较回溯法与动态规划的区…...

武汉昊衡科技OLI光纤微裂纹检测仪:高密度光器件的精准守护者
随着AI技术应用越来越广,算力需求激增,光通信系统正加速向小型化、高密度、多通道方向演进。硅光芯片、高速光模块等核心器件内部的光纤通道数量成倍增加,波导结构愈发精细,传统检测手段因分辨率不足、效率低下,难以精…...

SQL 函数进行左边自动补位fnPadLeft和FORMAT
目录 1.问题 2.解决 方式1 方式2 3.结果 1.问题 例如在SQL存储过程中,将1 或10 或 100 长度不足的时候,自动补足长度。 例如 1 → 001 10→ 010 100→100 2.解决 方式1 SELECT FORMAT (1, 000) AS FormattedNum; SELECT FORMAT(12, 000) AS Form…...

Tailwind CSS实战:快速构建定制化UI的新思路
引言 在当今快节奏的前端开发环境中,开发者不断寻找能够提高效率并保持灵活性的工具。Tailwind CSS作为一个功能型优先的CSS框架,正在改变开发者构建用户界面的方式。与Bootstrap和Material UI等传统组件库不同,Tailwind不提供预设组件&…...

【数据可视化-25】时尚零售销售数据集的机器学习可视化分析
🧑 博主简介:曾任某智慧城市类企业算法总监,目前在美国市场的物流公司从事高级算法工程师一职,深耕人工智能领域,精通python数据挖掘、可视化、机器学习等,发表过AI相关的专利并多次在AI类比赛中获奖。CSDN人工智能领域的优质创作者,提供AI相关的技术咨询、项目开发和个…...

UML 活动图深度解析:以在线购物系统为例
目录 一、UML 活动图的基本构成要素 二、题目原型 三、在线购物系统用户购物活动图详细剖析 (一)概述 (二)节点分析 三、注意事项 四、活动图绘画 五、UML 活动图在软件开发中的关键价值 六、总结 在软件开发与系统设计领…...
