线性代数—向量与矩阵的范数(Norm)
参考链接:
范数(Norm)——定义、原理、分类、作用与应用 - 知乎
带你秒懂向量与矩阵的范数(Norm)_矩阵norm-CSDN博客
什么是范数(norm)?以及L1,L2范数的简单介绍_l1 norm-CSDN博客
范数(Norm)是线性代数中的一个基本概念,用来度量一个向量的“长度”或“大小”。
(简单来说,范数告诉我们一个向量离原点有多远。)
- 向量范数 表征 向量空间中向量的大小,
- 矩阵范数 表征 矩阵引起变化的大小。
在机器学习中,范数常用于:
- 衡量预测误差(损失函数)
- 控制模型参数(正则化)
- 比较向量之间的相似度(归一化)
不同范数对应不同的学习目标:
- L1 控稀疏;
- L2 控幅度;
- L∞ 控最大值。
引入范数的原因
我们都知道,函数与几何图形往往是有对应的关系,这个很好想象,特别是在三维以下的空间内,函数是几何图像的数学概括,而几何图像是函数的高度形象化。
但当函数与几何超出三维空间时,就难以获得较好的想象,于是就有了映射的概念,进而引入范数的概念。当有了范数的概念,就可以引出两个向量的距离的定义,这个向量可以是任意维数的。
通过距离的定义,进而我们可以讨论逼近程度,从而讨论收敛性、求极限。
- 范数在计算机领域多用于:迭代过程中收敛性质的判断。
- 一般迭代前后步骤的差值的范数表示其大小,常用的是二范数,差值越小表示越逼近实际值,可以认为达到要求的精度,收敛。
总的来说,范数存在的意义是为了实现比较距离。
比如,在一维实数集合中,我们随便取两个点4和9,我们知道9比4大。
但是到了二维实数空间中,取两个点(1,0)和(3,4),这个时候就没法比较它们之间的大小,因为它们不是可以比较的实数。
于是引入范数这个概念,把(1,0)和(3,4)通过范数分别映射到实数1 和 5 (两个点分别到原点的距离),这样我们就比较这两个点了。
所以可以看到,范数其实是一个函数,它把不能比较的向量转换成可以比较的实数。
数学原理

向量的范数
在数学上,对于向量范数的定义,就是只要满足以下三条性质的函数,我们就可以称为它为范数。

(条件1的 的意思就是当且仅当的意思)
所以,范数的是一个宽泛的概念,有很多种,但是一般只会用到常用的范数。
线性代数中最有用的一些运算符是范数(norm)。 非正式地说,向量的范数是表示一个向量有多大。 这里考虑的大小(size)概念不涉及维度,而是分量的大小。
在线性代数中,向量范数是将向量映射到标量的函数
。 给定任意向量x,向量范数要满足一些属性。
性质3&4即正定,性质1即齐次,性质2即三角不等性。
向量的 L0范数
意义:非0元素个数

评价:L0范数表示向量中非零元素的个数。
L0范数的这个属性,使其非常适用于机器学习中的稀疏编码。
在特征选择中,通过最小化L0范数来寻找最少最优的稀疏特征项。
但是,L0范数的最小化问题是NP难问题。而L1范数是L0范数的最优凸近似,它比L0范数要更容易求解。
因此,优化过程将会被转换为更高维的范数(例如L1范数)问题。
向量的 L1范数 (曼哈顿范数、、最小绝对误差)
意义:各个元素的绝对值之和(向量x中非零元素的绝对值之和)
几何意义:实际走的 “横+竖” 的 “城市街道” 距离。

使用 L1范数可以度量两个向量间的差异,如绝对误差和(Sum of Absolute Difference):

由于L1范数的天然性质,对L1优化的解是一个稀疏解,
因此L1范数也被叫做 “Lasso regularization”(稀疏规则算子)。
通过L1可以实现特征的稀疏,去掉一些没有信息的特征,例如在对用户的电影爱好做分类的时候,用户有100个特征,可能只有十几个特征是对分类有用的,大部分特征如身高体重等可能都是无用的,利用L1范数就可以过滤掉。
向量的 L2范数 (欧几里得范数)
意义:每个元素平方和再平方根
 即
即 
像L1范数一样,L2也可以度量两个向量间的差异,如平方差和(Sum of Squared Difference):

评价:L2范数是最常用的范数,比如用的最多的度量距离欧氏距离就是一种L2范数。
在回归里面,有人把加了L2范数项的回归c称为“岭回归”(Ridge Regression),有人也叫它“权值衰减(weight decay)”。
它被广泛的应用在解决机器学习里面的过拟合问题:
- 通常被用来做优化目标函数的正则化项,防止模型为了迎合训练集而过于复杂造成过拟合的情况,从而提高模型的泛化能力。
为什么L2范数可以防止过拟合?回答这个问题之前,我们得先看看L2范数实际上是什么。
L2范数是指向量各元素的平方和然后求平方根。我们让L2范数的规则项最小,可以使得的每个元素都很小,都接近于0(L1范数会让它等于0,而L2范数是接近于0),这是有很大的区别的。而越小的参数说明模型越简单,越简单的模型则越不容易产生过拟合现象。为什么越小的参数说明模型越简单?
因为当限制了参数很小,实际上就限制了多项式某些分量的影响很小,即 相当于减少参数个数。
向量的 Lp范数 (一般形式)
意义:每个元素p次方和再p次方根
- L0、L1、L2 都是Lp范数的特例,分别对应P=0、1、2的情况;
- 可调节p控制范数行为(越大越趋近于L∞,即最大范数)
 即
即 
向量的 ∞范数 (最大范数)
意义:向量的 Lp范数的 p取无限大,即为向量的无穷范数,主要被用来度量向量元素的最大值。
- 取向量中最大绝对值作为长度。
- 有时用于鲁棒性分析。
![]()
PS
L2范数其实就是向量的标准内积,向量的长度一定是范数,长度是范数的充分条件,但不是必要条件,也就是说,范数不一定就是向量的长度。由
长度定义的性质可知,满足长度的定义要符合平行四边形。
举一个反例就可以证明非必要性:向量L1范数不满足平行四边形法则(A=(0,1)、B=(1,0))。
由内积决定的长度具有更丰富的几何结构。
总结
简单总结一下就是:
- L1范数: 为x向量各个元素绝对值之和,也叫“稀疏规则算”(Lasso regularization)。
- 比如 向量A=[1,-1,3], 那么A的L1范数为 |1|+|-1|+|3|.
- L2范数: 为x向量各个元素平方和的1/2次方(即 元素平方和的开根号)。
- L2范数又称Euclidean范数或者Frobenius范数
- Lp范数: 为x向量各个元素绝对值p次方和的1/p次方。
使用机器学习方法解决实际问题时,通常用L1或L2范数做正则化(regularization),从而限制权值大小,减少过拟合风险。特别是在使用梯度下降来做目标函数优化时。
L1正则化产生稀疏的权值,L2正则化产生平滑的权值为什么会这样?
在支持向量机学习过程中,L1范数实际是一种对于成本函数求解最优的过程,因此,L1范数正则化通过向成本函数中添加L1范数,使得学习得到的结果满足稀疏化,从而方便提取特征。
- L1范数可以使权值稀疏,方便特征提取。
- L2范数可以防止过拟合,提升模型的泛化能力。
L1和L2正则先验分别服从什么分布
- L1是拉普拉斯分布。
- L2是高斯分布。
矩阵的范数
跟向量的范数定义类似,只不过矩阵的范数的性质比向量的范数性质多了一条相容性。
我们直接引出矩阵的范数定义:

矩阵范数的第三条性质也称为加法相容性,第四条是乘法相容性,前提都是矩阵之间可以进行加法或乘法的运算。
矩阵的 1-范数(列模)
意义:矩阵的 列向量的和 的最大值,即 A的每列元素绝对值之和 的最大值,也称为A的列范数。

矩阵的 2-范数(谱模)
意义: 矩阵的最大特征值的开平方,也称谱范数。
- 特征值相当于是两个维度的压缩,相当于是从矩阵的维度里面找到最大的。

矩阵的 ∞范数(行模)
意义:矩阵的 行向量的和 的最大值,即 A的每行元素绝对值之和 的最大值,也称为A的行范数。

矩阵的 F-范数
意义:Frobenius范数,即矩阵元素绝对值的平方和再开平方。类似于向量的L2范数。
 即
即 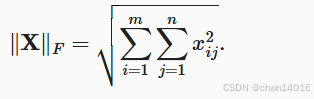
也可以描述为:

总结
简单总结一下就是:
- L1范数: 列范数,矩阵的 列向量的和 的最大值,即 A的每列元素绝对值之和 的最大值。
- L2范数:
矩阵的最大特征值的开平方,也称谱范数。
- 特征值相当于是两个维度的压缩,相当于是从矩阵的维度里面找到最大的。
- L∞范数: 行范数,矩阵的 行向量的和 的最大值,即 A的每行元素绝对值之和 的最大值。
- Lf范数: Frobenius范数,类似于向量的L2范数,矩阵元素平方和再开平方。
范数的作用
| 作用领域 | 用途 | 说明 |
|---|---|---|
| 向量距离 | 度量两个点或向量之间的“距离” | 用于损失函数、相似度计算 |
| 模型正则化 | 控制模型复杂度,防止过拟合 | 通过惩罚大参数避免学习噪声 |
| 向量归一化 | 把向量缩放到单位长度 | 常用于余弦相似度比较 |
| 稀疏表示 | 用最少的非零值表达信息 | L1 正则可自动“筛选特征” |
在机器学习中的实际应用
✅ 1. 损失函数中的误差度量
| 类型 | 范数 | 说明 |
|---|---|---|
| MAE(平均绝对误差) | L1 | 鲁棒,对异常值不敏感 |
| MSE(均方误差) | L2 | 常用,惩罚大误差更重 |
✅ 2. 模型正则化(Regularization)
| 类型 | 正则项 | 功能 |
|---|---|---|
| L1 正则(Lasso) | (\lambda \sum | \theta_i |
| L2 正则(Ridge) | λ∑θi2\lambda \sum \theta_i^2 | 缓和过拟合,不会让参数变0,但压小 |
✅ 3. 向量归一化(Normalization)

✅ 4. 稀疏建模(Sparse Modeling)
- 在某些应用中,希望模型只依赖少数几个特征(稀疏性):
- 如文本分类、基因数据分析;
使用 L1 正则可以“自动让不重要的参数变成 0”;
- L1 是稀疏性建模的核心工具。
面试范数相关常见提问汇总 + 答题思路
✅ 一、基础概念类问题(定义 + 原理)
❓Q1:解释一下什么是范数吗?
答题思路:
范数是一种用来衡量向量“大小”或“长度”的函数,它在机器学习中用于表示误差、距离、向量归一化或正则化。常见的范数有 L1 范数、L2 范数等,分别对应不同的应用需求。
❓Q2:L1 范数和 L2 范数的区别是什么?你更偏向哪一个?
答题思路:
- L1 范数是所有元素的绝对值之和,鼓励模型稀疏;
- L2 范数是所有元素平方和的平方根,鼓励整体平滑;
- 如果任务要求模型可解释性强、特征选择重要,我会选择 L1;
- 如果任务对稳定性更敏感,比如图像处理,我倾向 L2。
✅ 二、应用场景类问题(结合模型/正则)
❓Q3:在损失函数中为什么有时使用 L1 有时使用 L2?
答题思路:
- L1(如 MAE)更稳健,适合对异常值敏感的任务;
- L2(如 MSE)更常见,对大误差惩罚更重;
- 如果数据中有 outlier,建议使用 L1;
- 如果更关注整体误差稳定性,可以使用 L2。
❓Q4:正则化中 L1 和 L2 分别起什么作用?
答题思路:
- L1 正则通过绝对值惩罚,会使某些参数收缩为 0,实现特征选择;
- L2 正则通过平方惩罚,防止参数过大,减少过拟合;
- L1 更适合用于高维稀疏建模(如文本分类),L2 更适合神经网络等连续模型。
✅ 三、原理理解类问题(深入推导)
❓Q5:为什么 L2 正则不产生稀疏性,但 L1 会?
答题思路:
- 从几何角度讲,L1 范数的等值线是菱形,容易与损失函数的最优点交于坐标轴;
- 而 L2 范数的等值线是圆形,更倾向于“均匀缩小所有参数”而不是让某些为 0;
- 所以 L1 更容易“压掉”不重要的特征,让参数变为0。
❓Q6:你知道范数与梯度下降优化的关系吗?
答题思路:
- 在添加正则化的损失函数中,比如 L2,会影响梯度更新方向;
- L2 会加上 λθ\lambda \theta 项,等于对参数有一个“缩小”的趋势;
- L1 的梯度是非连续的(不可导点),所以常用次梯度或特殊优化方法处理。
✅ 四、项目/实践类问题(结合实际应用)
❓Q7:在项目中有没有用到范数?怎么选的 L1 / L2?
答题思路(举例):
- “在我做房价预测项目中,我使用了 L1 正则化进行特征选择,发现有多个冗余特征被自动归零,提升了模型解释性。”
- “而在另一个图像复原项目中,我使用了 L2 损失函数和 L2 正则,因为目标是尽可能还原每个像素值,不允许过大偏差。”
❓Q8:若模型过拟合了,会怎么用范数应对?
答题思路:
- 我会通过添加正则化项(L1/L2)来约束模型参数的规模;
- 如果模型很复杂,特征维度很高,我会尝试 L1 来让模型自动做特征选择;
- 如果我关注模型的稳定性和泛化性能,我会使用 L2 控制参数幅度。
✅ 五、开放性问题(考察综合素质)
❓Q9:如果我说 L2 正则是控制模型复杂度的“软剪枝”,你怎么理解?
答题思路:
- 软剪枝指的是“不强制为0,而是控制其变小”;
- L2 不会像 L1 一样使参数归零,但会持续压缩大的权重;
- 这有助于模型在保持全部特征的情况下减少过拟合。
快速知识卡片(可打印记忆)
| 项 | L1 范数 | L2 范数 |
|---|---|---|
| 公式 | (\sum | x_i |
| 名称 | 曼哈顿距离 | 欧几里得距离 |
| 特点 | 稀疏、鲁棒 | 平滑、常用 |
| 正则化应用 | Lasso(特征选择) | Ridge(稳定优化) |
| 适用场景 | 高维稀疏建模 | 连续模型控制复杂度 |
| 损失函数 | MAE | MSE |
| 面试关键词 | 特征选择、正则稀疏性 | 权重控制、余弦相似度归一化 |
相关文章:

线性代数—向量与矩阵的范数(Norm)
参考链接: 范数(Norm)——定义、原理、分类、作用与应用 - 知乎 带你秒懂向量与矩阵的范数(Norm)_矩阵norm-CSDN博客 什么是范数(norm)?以及L1,L2范数的简单介绍_l1 norm-CSDN博客 范数(Norm…...
)
Umi-OCR项目(1)
最近接触到了一个项目,我在想能不能做出点东西出来。 目标:识别一张带表格的图片,要求非表格内容和表格内容都要识别得很好,并且可视化输出为word文档。 下面是第一步的测试代码,测试是否能够调用ocr能力。 import re…...
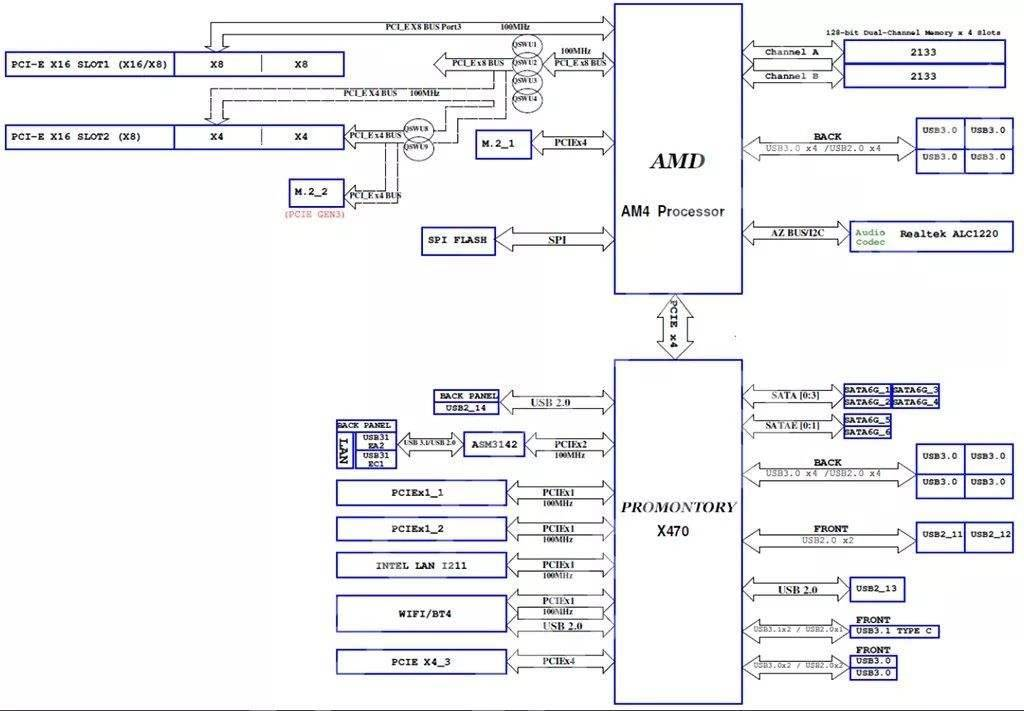
【业务领域】电脑主板芯片电路结构
前言 由前几期视频合集(零基础自学计算机故障排除—7天了解计算机开机过程),讲解了POST的主板软启动过程;有不少网友留言、私信来问各种不开机的故障,但大多网友没能能过我们的这合集视频,很好的理清思路,那这样的情况…...

pandas读取Excel数据(.xlsx和.xls)到treeview
对于.xls文件,xlrd可能更合适,但需要注意新版本的xlrd可能不支持xlsx,不过用户可能同时需要处理两种格式,所以可能需要结合openpyxl和xlrd?或者直接用pandas,因为它内部会处理这些依赖。 然后,…...

【Nginx】负载均衡配置详解
Nginx作为高性能的HTTP服务器和反向代理服务器,提供了强大的负载均衡功能。本文将详细介绍Nginx负载均衡的配置方法和相关策略。 一、基础负载均衡配置 1.单服务示例配置 配置nginx.conf模块 在Nginx配置文件中定义upstream模块: worker_processes a…...

JVM——垃圾收集策略
GC的基本问题 什么是GC? GC 是 garbage collection 的缩写,意思是垃圾回收——把内存(特别是堆内存)中不再使用的空间释放掉;清理不再使用的对象。 为什么要GC? 堆内存是各个线程共享的空间,…...

马克·雷伯特:用算法让机器人飞奔的人
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 马克雷伯特:用算法让机器人飞奔的人 一、天才的起点 在机器人领域,有一个名字如雷贯耳——马克雷伯特(Marc Raibert)。作为波士顿动力公司(Boston…...
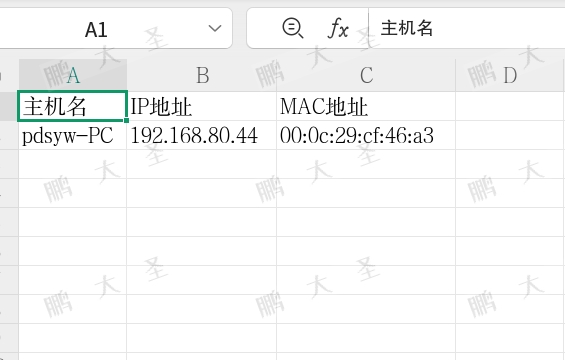
信创系统资产清单采集脚本:主机名+IP+MAC 一键生成 CSV
原文链接:信创系统资产清单采集脚本:主机名IPMAC 一键生成 CSV Hello,大家好啊!今天给大家带来一篇在信创终端操作系统上自动批量采集主机名、IP 和 MAC 并导出为 CSV 表格的实战文章!本方案使用 sshpass 和 Bash 脚本…...

SpringBoot获取用户信息常见问题(密码屏蔽、驼峰命名和下划线命名的自动转换)
文章目录 一、不返回password字段二、返回的createTime和updateTime为空原因解决:开启驼峰命名和下划线命名的自动转换 设置返回的日期格式 一、不返回password字段 在字段上面添加JsonIgnore注解即可 JsonIgnore // 在把对象序列化成json字符串时,忽略…...

小刚说C语言刷题—1602总分和平均分
1.题目描述 期末考试成绩出来了,小明同学语文、数学、英语分别考了 x、y、z 分,请编程帮助小明计算一下,他的总分和平均分分别考了多少分? 输入 三个整数 x、y、z 分别代表小明三科考试的成绩。 输出 第 11行有一个整数&…...
-cmake/CMakeLists.txt的编译使用教程)
C++编译之(5)-cmake/CMakeLists.txt的编译使用教程
C++编译之(5)-cmake/CMakeLists.txt的编译使用教程 上一节,点这里 1、如何查看cmake的配置参数 那么如何查看当前配置的参数呢,我们可以使用-L参数 cmake .. -L # cmake .. -LAH完全使用命令行,则可以通过多次重复使用cmake … -DOPTION1=ON -D OPTION2=ON配置制定选项;并…...

Mac下安装Python3,并配置环境变量设置为默认
下载Python 访问Python官方网站 https://www.python.org/ 首先获得python3安装路径 执行命令: which python3 以我这台电脑为例,路径为:/Library/Frameworks/Python.framework/Versions/3.9/bin/python3 编辑 bash_profile 文件 然后用 vim 打…...

Linux-04-用户管理命令
一、useradd添加新用户: 基本语法: useradd 用户名:添加新用户 useradd -g 组名 用户:添加新用户到某个组二、passwd设置用户密码: 基本语法: passwd 用户名:设置用户名密码 三、id查看用户是否存在: 基本语法: id 用户名 四、su切换用户: 基本语法: su 用户名称:切换用…...

【进阶】--函数栈帧的创建和销毁详解
目录 一.函数栈帧的概念 二.理解函数栈帧能让我们解决什么问题 三.相关寄存器和汇编指令知识点补充 四.函数栈帧的创建和销毁 4.1.调用堆栈 4.2.函数栈帧的创建 4.3 函数栈帧的销毁 一.函数栈帧的概念 --在C语言中,函数栈帧是指在函数调用过程中,…...

Hadoop伪分布式模式搭建全攻略:从环境配置到实战测试
引言 作为大数据生态的基石,Hadoop凭借其高可靠性、扩展性成为分布式计算的首选框架。本文将手把手带你完成Hadoop伪分布式模式部署,通过单节点模拟集群环境,为后续学习MapReduce、YARN等核心组件打下基础 目录 引言 Hadoop 发展历史 1.1 起源(2002–2005) 1.1 安装JDK…...

Transformer:颠覆深度学习的架构革命与技术演进
2017年,谷歌团队在论文《Attention Is All You Need》中提出的Transformer架构,彻底改变了人工智能对序列数据的处理范式。它不仅解决了传统循环神经网络(RNN)的长期依赖和并行化难题,更催生了BERT、GPT等划时代模型&a…...

【一】 基本概念与应用领域【数字图像处理】
考纲 文章目录 1 概念2005甄题【名词解释】2008、2012甄题【名词解释】可考题【简答题】可考题【简答题】 2 应用领域【了解】2.1 伽马射线成像【核医学影像】☆2.2 X射线成像2.3 紫外波段成像2.4 可见光和红外波段成像2.5 微波波段成像2.6 无线电波段成像2.7 电子显微镜成像2…...

NU1680低成本、无固件、高集成度无线充电电源接收器
无线充电 电子产品具有无线充电功能使用会更便利,介绍一款低成本、无固件、高集成度无线充电电源接收器NU1680 原理图和BOM可点绑定资源下载,LC部分电容建议X7R。 Load空载切满载测试 (CC Mode) – 尽量保证电子负载没有过冲 – 电子负载不要从0到满…...

JVM 内存分配策略
引言 在 Java 虚拟机(JVM)中,内存分配与垃圾回收是影响程序性能的核心机制。内存分配的高效性直接决定了对象创建的速率,而垃圾回收策略则决定了内存的利用率以及系统的稳定性。为了在复杂多变的应用场景中实现高效的内存管理&am…...

2025MathorCup数学应用挑战赛B题
目录 模型建立与求解 1.问题一的模型建立与求解 1.1 搬迁补偿模型设计 1.2 住户是否搬迁的应对策略与分析 1.3 定量讨论 2.问题二的模型建立与求解 2.1 搬迁方案模型的优化介绍 2.2 模型的评估 2.3 模型结果 3.问题三的模型建立与求解 3.1 拐点存在性分析模型的建立 3.2 模型的…...

组件的基本知识
组件 组件的基本知识 组件概念组成步骤好处全局注册生命周期scoped原理 父子通信步骤子传父 概念 就是将要复用的标签,抽离放在一个独立的vue文件中,以供主vue文件使用 组成 三部分构成 template:HTML 结构 script: JS 逻辑 style: CSS 样…...

Origin绘图操作:图中迷你图绘制
一、背景描述 Origin绘图时,局部数据变化较小,在整体图片中表现为局部曲线重叠在一起,图中y1和y2在x0-2时重叠在一起,需要将局部放大,绘制迷你图 二、实现方法 1.在左边工具栏选择放大镜,按住ctrl在图中…...

数据升降级:医疗数据的“时空穿梭“系统工程(分析与架构篇)
一、核心挑战与量化分析 1. 版本演化困境的深度解析 (1) 格式断层的结构化危机 数据转换黑洞:某医疗信息平台(2021-2023)统计显示: 数据类型CDA R1→R2转换失败率R2→FHIR转换失败率关键失败点诊断记录28.4%19.7%ICD编码版本冲突(18.7%)用药记录15.2%12.3%剂量单位标准化…...
【GESP】C++三级练习 luogu-B2089 数组逆序重存放
GESP三级练习,一维数组练习(C三级大纲中5号知识点,一维数组),难度★☆☆☆☆。 题目题解详见:https://www.coderli.com/gesp-3-luogu-b2089/ 【GESP】C三级练习 luogu-B2089 数组逆序重存放 | OneCoderGE…...

Copilot 上线深度推理智能体 Researcher
近日,微软推出两款首创的工作场景推理智能体:Researcher(研究员)和Analyst(分析师)。它们能以安全合规的方式访问您的工作数据(包括邮件、会议、文件、聊天记录等)及互联网信息&…...

QDrant数据构造及增删改查
QDrant数据构造及增删改查 一、PointStruct介绍 PointStruct 是一种结构体(或数据类),通常用于表示: 向量数据库中的一个数据点(Vector Point),包括它的 ID、向量值(vector embedd…...

日常开发小Tips:后端返回带颜色的字段给前端
一般来说,展示给用户的字体格式,都是由前端控制,展现给用户; 但是当要表示某些字段的数据为异常数据,或者将一些关键信息以不同颜色的形式呈现给用户时,而前端又不好判断,那么就可以由后端来控…...

如何在WordPress网站中设置双重验证,提升安全性
随着互联网的不断进步,网站的安全问题越来越受到重视。尤其对于WordPress这样常用的建站平台,安全性显得尤为重要。尽管WordPress自带一定的安全性,但仅依靠用户名和密码的登录方式仍然存在风险。因此,启用“双重验证”便成为了提…...

Python 虚拟环境管理:venv 与 conda 的选择与配置
文章目录 前言一、虚拟环境的核心价值1.1 依赖冲突的典型场景1.2 隔离机制实现原理 二、venv 与 conda 的架构对比2.1 工具定位差异2.2 性能基准测试(以创建环境 安装 numpy 为例) 三、venv 的配置与最佳实践3.1 基础工作流3.2 多版本 Python 管理 四、…...

8.Android(通过Manifest配置文件传递数据(meta-data))
配置文件 <?xml version"1.0" encoding"utf-8"?> <manifest xmlns:android"http://schemas.android.com/apk/res/android"xmlns:tools"http://schemas.android.com/tools"><applicationandroid:allowBackup"tr…...

