【递归、搜索和回溯】递归、搜索和回溯介绍及递归类算法例题
个人主页 : zxctscl
专栏 【C++】、 【C语言】、 【Linux】、 【数据结构】、 【算法】
如有转载请先通知
文章目录
- 递归、搜索和回溯
- 递归
- 搜索VS 深度优先遍历 VS 深度优先搜索 VS 宽度优先遍历 VS 宽度优先搜索 VS 暴搜
- 回溯与剪枝
- 1 面试题 08.06. 汉诺塔问题
- 1.1 分析
- 1.2 代码
- 2 21. 合并两个有序链表
- 2.1 分析
- 2.2 代码
- 2.3 总结
- 3 206. 反转链表
- 3.1 分析
- 3.2 代码
- 4 24. 两两交换链表中的节点
- 4.1 分析
- 4.2 代码
- 5 50. Pow(x, n)
- 5.1 分析
- 5.2 代码
递归、搜索和回溯
搜索是递归的一个分支,回溯是搜索里面的分支。
递归
-
什么是递归?
在数据结构二叉树、快排和归并都有提到
递归就是函数自己调用自己的情况 -
为什么会用到递归
二叉树的后序遍历:左子树、右子树、根
在快排中,先选择一个基准元素将数组分成两部分,左边排一下序,右边排一下序
在归并排序中,选择一个中间点,把数组平分,先让左边排一下序,再让右边排一下序,再把两个有序数组合并

递归的本质:
主问题->相同的子问题
子问题->相同的子问题 -
如何理解递归
(1)递归展开的细节图
(2)二叉树的题目
(3)宏观看待递归过程:
一、不要在意递归细节展开图
二、把递归的函数当成一个黑盒(具体里面如何操作的并不关心,只要能输出结果)
三、相信这个黑盒一定能完成这个任务

-
如何写好递归
(1)先找到相同的子问题->函数头的设计
(2)只关心某一个子问题是如何解决的->函数体的书写
(3)注意一下递归函数的出口即可
搜索VS 深度优先遍历 VS 深度优先搜索 VS 宽度优先遍历 VS 宽度优先搜索 VS 暴搜
-
深度优先遍历 VS 深度优先搜索->
dfs
宽度优先遍历 VS 宽度优先搜索->bfs
一定程度上等同
遍历是形式,目的是搜索

-
关系图
暴力枚举一遍所有的结果
搜索(也叫暴搜)分为两种:dfs、 bfs
递归主要是dfs -
拓展搜索问题
全排列 树状图

回溯与剪枝
- 回溯
回溯本质就是深搜
1 面试题 08.06. 汉诺塔问题

1.1 分析
-
题目解析
中间摆放的时候必须是小盘子在大盘子的上面 -
算法原理
(1)如何解决汉洛塔问题?
当N=1,直接把A上面的盘子放到C上。
当N=2,想要把最大的盘子放到C上,此时先得把上面的小盘子放到B上,当把A剩下的大盘子直接移动到C上后,再将B上的小盘子放到C上。
当N=3时候,首先把A最下面盘子移动到C,前提就得将A上面的2个盘子放到B上(就像N=2时,把上面两个盘子借助C移到B上)再将A最下面的盘子放到C上,最后把B上的盘子移到C上。
当N=4时,首先把A最下面盘子移动到C,前提就得将A上面的3个盘子(当做一个整体)放到B上(就像N=3时,把上面两个盘子借助C移到B上)再将A最下面的盘子放到C上,最后把B上的盘子移到C上。
…
当N=n,也同样是首先把A最下面盘子移动到C,前提就得将A上面的n-1个盘子(当做一个整体)放到B上(就像N=n-1时,把上面两个盘子借助C移到B上)再将A最下面的盘子放到C上,最后把B上的盘子移到C上。

(2)为什么用递归?
大问题->相同问题的子问题
子问题->相同问题的子问题
(3)如何编写递归代码?
一、重复子问题->函数头
先把X柱子上的盘子,借助Y柱子,转移到Z柱子上
需要三个柱子,还有盘子的数量,就需要传四个参数
void dfs(X,Y,Z,int n)
二、只关心某一个子问题在做什么->函数体
(1)将X上面n-1盘子,借助Z,转移到Y上dfs(X,Z,Y,n-1)
(2)把A最下面盘子移到Z上
(3)再将Y上n-1个盘子借助X移到Z上dfs(Y,X,Z,n-1)

三、递归出口
当N=1时,把X上盘子放到Z上

-
编写代码
-
递归的细节展开图

1.2 代码
class Solution {
public:void hanota(vector<int>& A, vector<int>& B, vector<int>& C) { dfs(A,B,C,A.size()); }void dfs(vector<int>& A, vector<int>& B, vector<int>& C,int n){if(n==1){C.push_back(A.back());A.pop_back();return;}dfs(A,C,B,n-1);C.push_back(A.back());A.pop_back();dfs(B,A,C,n-1);}
};
2 21. 合并两个有序链表

2.1 分析
算法原理
解法:递归
两个链表都是升序,找两个链表头结点中较小的节点作为返回的头节点。
当选择头节点之后,就是将剩下的两个链表合并

(1)重复子问题->函数头
合并两个有序链表 Node*dfs(l1,l2)
(2)只关心某一个子问题在做什么事情->函数体的设计
一、比大小
二、如果l1较小 :l1->next=dfs(l1->next,l2)
三、return l1
(3)递归出口
谁为空返回另一个

2.2 代码
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2){if(list1==nullptr)return list2;if(list2==nullptr)return list1;if(list1->val<=list2->val){list1->next=mergeTwoLists(list1->next,list2);return list1;}else{list2->next=mergeTwoLists(list1,list2->next);return list2;}}};
2.3 总结
- 递归VS循环 什么时候用循环舒服?什么时候用递归舒服?
递归和循环都是重复子问题,递归和循环之间可以相互转换
递归图越复杂,递归就越舒服
- 递归VS深搜
递归展开图,其实就是对一棵树做一次深度优先搜索遍历(dfs)

3 206. 反转链表

3.1 分析
解法:递归
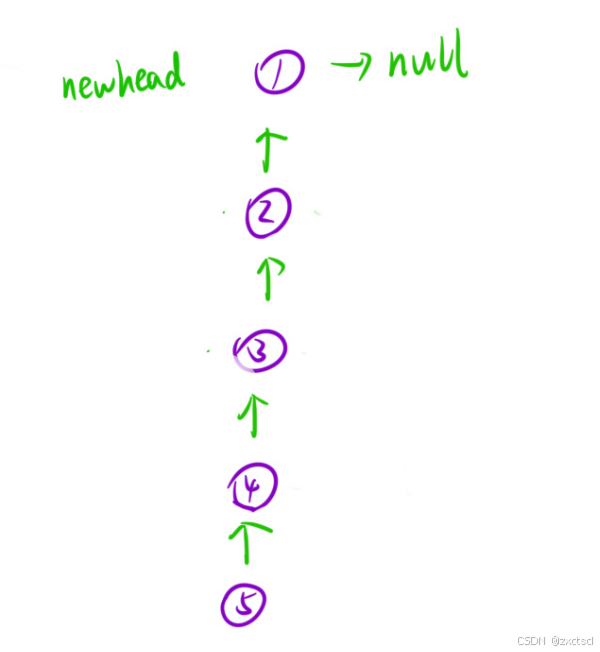
第一个视角:从宏观角度
- 把当前节点后面链表先逆置,并且把头结点返回;
- 把当前节点添加到逆置链表的后面
- 当遇到null就返回

第二个视角:将链表看成一棵树
先找到叶子结点,再返回

3.2 代码
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* reverseList(ListNode* head) {if(head==nullptr||head->next==nullptr)return head;ListNode* newhead=reverseList(head->next);head->next->next=head;head->next=nullptr;return newhead;}
};
4 24. 两两交换链表中的节点

4.1 分析
解法:递归
视角:从宏观角度看待递归
想要两两逆置,把后面的那堆先两两逆置一下,后面的调用完dfs后,再返回后面部分的头结点,再把前面两个交换一下,把交换后的连起来。


4.2 代码
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* swapPairs(ListNode* head) {if (head == nullptr || head->next == nullptr)return head;ListNode* tmp = swapPairs(head->next->next);ListNode* ret = head->next;head->next->next = head;head->next = tmp;return ret;}
};
5 50. Pow(x, n)

5.1 分析
解法:一、暴力循环
对于太大的幂是会超时的
二、快速幂
实现快速幂:(1)递归(2)循环
这里用递归
如果快速得到3的16次方,得到3的8次方就行,要3的8次方得到3的4次方就行,要得到3的4次方,得到3的2次方就行,要得到3,就直接3乘1就行。这里时间复杂度就是logN
那么如果除不进时,21/2除不进,就能可以分为3的10次方乘3的10次方再乘3就行,一直这样

(1)重复子问题->函数头
int pow(x,n)
(2)只关心某一个子问题在做什么事情->函数体的设计
先求出n/2的次方是多少: tmp=pow(x,n/2)
再判断一下n/2能不能整除,不能整除再成上x:return n%2==0?tmp*tmp*x
(3)递归出口
如果n等于0,就返回1
细节问题:
-
n可能是负数
要提前把负数转成正数,再用1除一下

-
n可能是-2^31
-2^31负数太大,转成正数会存不下,int正整数最大是2^31-1
可以提前把n的类型强转为long long

5.2 代码
class Solution {
public:double myPow(double x, int n) {return n<0?1.0/pow(x,-(long long)n):pow(x,n);}double pow(double x, int n){if(n==0)return 1.0;double tmp=pow(x,n/2);return n%2==0?tmp*tmp:tmp*tmp*x; }
};
有问题请指出,大家一起进步!!!
相关文章:

【递归、搜索和回溯】递归、搜索和回溯介绍及递归类算法例题
个人主页 : zxctscl 专栏 【C】、 【C语言】、 【Linux】、 【数据结构】、 【算法】 如有转载请先通知 文章目录 递归、搜索和回溯递归搜索VS 深度优先遍历 VS 深度优先搜索 VS 宽度优先遍历 VS 宽度优先搜索 VS 暴搜回溯与剪枝 1 面试题 08.06. 汉诺塔问题1.1 分析…...

JDK8 HashMap红黑树退化为链表的机制解析
目录 1、数据结构: 2、Fail-Fast机制 2.1、核心作用 2.2、实现原理 2.3、触发场景 2.4、实现细节 2.5、对比 2.6、注意事项 3、核心结论 4、转化安全机制 4.1. 触发场景 4.2. 转换过程 4.3. 并发安全机制 5、设计原因 5.1. 性能权衡 5.2. 空间局部性…...
【基础】模型上下文协议(Model Context Protocol, MCP)根本原理与工作机制详解
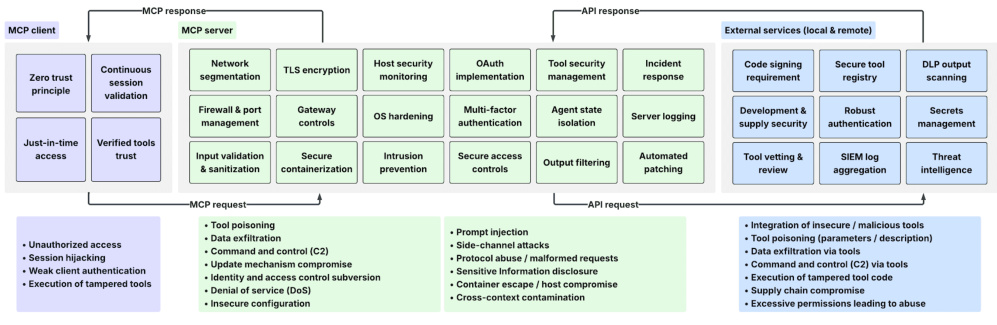
一、MCP的根本原理 模型上下文协议(MCP)是一种标准化接口协议,旨在解决AI系统(尤其是大型语言模型,LLM)与外部工具、数据源之间的交互碎片化问题。其核心原理可以概括为以下三点: 统一接口抽象…...

霸王茶姬微信小程序自动化签到系统完整实现解析
霸王茶姬微信小程序自动化签到系统完整实现解析 技术栈:Node.js 微信小程序API MD5动态签名 一、脚本全景架构 功能模块图 #mermaid-svg-0vx5W2xo0IZWn6mH {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-s…...

北斗导航 | RTKLib中重难点技术,公式,代码
Rtklib 一、抗差自适应卡尔曼滤波1. **核心难点**2. **公式与代码实现**二、模糊度固定与LAMBDA算法1. **核心难点**2. **LAMBDA算法实现**3. **部分模糊度固定技术**三、伪距单点定位与误差修正1. **多系统多频点修正**2. **接收机钟差与系统间偏差**四、动态模型与周跳处理1.…...

p2p虚拟服务器
ZeroTier Central ✅ 推荐工具:ZeroTier(免费、稳定、跨平台) ZeroTier 可以帮你把多台设备(无论是否跨网)加入一个虚拟局域网,彼此间可以像在同一个 LAN 中通信,UDP 视频、文件传输、SSH 等都…...
)
Python 爬虫基础入门教程(超详细)
一、什么是爬虫? 网络爬虫(Web Crawler),又称网页蜘蛛,是一种自动抓取互联网信息的程序。爬虫会模拟人的浏览行为,向网站发送请求,然后获取网页内容并提取有用的数据。 二、Python爬虫的基本原…...

python实现点餐系统
使用python实现点餐系统的增加菜品及价格,删除菜品,查询菜单,点菜以及会员折扣价等功能。 代码: 下面展示一些 内联代码片。 # coding utf-8menu {拍黄瓜: 6, 小炒肉: 28, 西红柿炒蛋: 18, 烤鱼: 30, 红烧肉: 38, 手撕鸡: 45,…...

(三)毛子整洁架构(Infrastructure层/DapperHelper/乐观锁)
文章目录 项目地址一、Infrastructure Layer1.1 创建Application层需要的服务1. Clock服务2. Email 服务3. 注册服务 1.2 数据库服务1. 表配置Configurations2. Respository实现3. 数据库链接Factory实现4. Dapper的DataOnly服务实现5. 所有数据库服务注册 1.3 基于RowVersion的…...

探索Stream流:高效数据处理的秘密武器
不可变集合 stream流 Stream流的使用步骤: 先得到一条Stream流(流水线),并把数据放上去 使用中间方法对流水线上的数据进行操作 使用终结方法对流水线上的数据进行操作 Stream流的中间方法 注意1:中间方法࿰…...

git高效杀器——cz-customizable 搭配 commitlint
What is cz-customizable and commitlint? cz-customizable 一款可定制化的Commitizen插件(也可作为独立工具),旨在帮助创建如约定式提交规范的一致性提交消息。commitlint commitlint 是一个用于检查 Git 提交信息的工具,它可以帮助开发者保持提交信息的规范性和一致性。…...

虚拟机ubantu20.04系统桥接模式下无法ping通外网,但可以ping通本机的解决方案
1.出现的问题: 虚拟机ubantu20.04系统桥接模式下无法ping通外网,但可以ping通本机。 2.解决方案: 如果 DHCP 未分配 IP 地址,可以手动配置静态 IP: 1.编辑网络配置文件: sudo nano /etc/netplan/01-netcfg.yaml 2…...

日常知识点之随手问题整理(思考单播,组播,广播哪个更省带宽)
新入职的公司在某些场景下无脑使用组播技术,自己突然就意识到一个问题:单播,组播,广播,哪个更省带宽? 有所收获,做点笔记,仅仅是个人理解~ 1:简单理解 单播࿱…...

qtcreater配置opencv
我配置opencv不管是按照网上的教程还是deep seek发现都有些问题,下面是我的配置方法以及实践成功的心得 电脑环境 windows平台qt6 下载 我这里直接提供官网下载地址:https://opencv.org/releases/ 我下载的是最新版,下载后是一个.exe文件…...

详解 c++17 重载类 overload的每一条语句,附实例.
author: hjjdebug date: 2025年 05月 09日 星期五 16:21:03 CST description: 详解 c17 重载类 overload的每一条语句 文章目录 1. template 模板类.2. class... Ts 是什么意思?3. template<class... Ts> 是什么意思?4. overload 是什么?5. Ts...…...

机器学习-数据集划分和特征工程
一.数据集划分 API函数: sklearn.model_selection.train_test_split(*arrays,**options) 参数: - arrays:多个数组,可以是列表,numpy数组,也可以是dataframe数据框等 - options:&…...

MySQL C API高效编程:C语言实现数据库操作的深入解析
知识点【MySQL C API】 1、头文件及MYSQL * 句柄 //头文件 #include <mysql/mysql.h>1、MYSQL MYSQL是一个结构体,封装了与数据库连接相关的所有状态,配置和数据。 2、MYSQL *的本质 类似于 FILE*,代表一个与数据库连接的通道&…...

MySQL初阶:数据库约束和表的设计
数据库约束 数据库约束是针对数据库中的表中的数据进行施加规则和条件,用于确保数据的准确性和可靠性。 数据库约束类型 1)not null 非空类型 :指定非空类型的列不能存储null,如果插入的数据是null便会报错。 2)de…...

LeetCode 解题思路 47(最长回文子串、最长公共子序列)
解题思路: dp 数组的含义: dp[i][j] 是否为回文子串。递推公式: dp[i][j] s.charAt(i) s.charAt(j) && dp[i 1][j - 1]。dp 数组初始化: 单字符 dp[i][i] true,双字符 dp[i][i 1] s.charAt(i) s.charA…...

左支座加工工艺与钻φ25孔专用夹具设计
1 零件结构与工艺分析 1.1 零件结构特征 本左支座为典型箱体类零件,采用HT200灰铸铁铸造毛坯。主体结构包含: 20015080mm安装基面 2φ12定位孔(公差H7) φ250.02主轴承孔(表面粗糙度Ra1.6) 4M10螺纹安…...

基于Qwen-14b的基础RAG实现及反思
1、概览 本文主要介绍RAG的基础实现过程,给初学者提供一些帮助,RAG即检索增强生成,主要是两个步骤:检索、生成,下面将基于这两部分进行介绍。 2、检索 检索的主要目的是在自定义的知识库kb中查询到与问题query相关的候…...

嵌入式培训之C语言学习完(十七)结构体、共用体、枚举、typedef关键字与位运算
目录 一、结构体(struct关键字) (一)声明一个结构体数据类型 (二)结构体的成员初始化与赋值 a、结构体变量赋值 b、结构体成员初始化 c、结构体的定义形式 (三)考点ÿ…...

极狐GitLab 命名空间的类型有哪些?
极狐GitLab 是 GitLab 在中国的发行版,关于中文参考文档和资料有: 极狐GitLab 中文文档极狐GitLab 中文论坛极狐GitLab 官网 命名空间 命名空间在极狐GitLab 中组织项目。因为每一个命名空间都是单独的,您可以在多个命名空间中使用相同的项…...

N6715C 基础型定制配置直流电源分析仪
N6715C 基础型定制配置直流电源分析仪 综述 N6715C 是一款可定制的直流电源分析仪系统,在装运之前已经过全面测试并组装完毕。 每台 N6715C 包括一个 N6705C 主机和 1 至 4 个模块。 模块作为 E6715C 的选件订购。 主要特点 ◆ ◆ 4 插槽主机最多可安装 4 个模块…...

4.1【LLaMA-Factory 实战】医疗领域大模型:从数据到部署的全流程实践
【LLaMA-Factory实战】医疗领域大模型:从数据到部署的全流程实践 一、引言 在医疗AI领域,构建专业的疾病诊断助手需要解决数据稀缺、知识专业性强、安全合规等多重挑战。本文基于LLaMA-Factory框架,详细介绍如何从0到1打造一个垂直领域的医…...

《软件项目经济性论证报告模板:全面解析与策略建议》
《软件项目经济性论证报告模板:全面解析与策略建议》 一、引言 1.1 项目背景阐述 在数字化浪潮席卷全球的当下,各行业对软件的依赖程度日益加深。[行业名称] 行业也不例外,随着业务规模的不断扩张、业务复杂度的持续提升以及市场竞争的愈发激烈,对高效、智能、定制化软件…...

腾讯云:数字世界的“量子熔炉”与硅基文明引擎
一、算力拓扑学:重新定义空间的计算密度 腾讯云的算力网络正在突破经典物理限制,其分布式架构通过“量子化”资源调度实现超维计算: 虚拟化跃迁:基于KVM的轻量级虚拟化技术,将单台物理服务器切割为百…...

Android 项目中配置了多个 maven 仓库,但依赖还是下载失败,除了使用代理,还有其他方法吗?
文章目录 前言解决方案gradlemaven 仓库 前言 我们在Android 开发的过程中,经常会遇到三方依赖下载不下来的问题。一般情况下我们会在项目的build.gradle文件中配置多个 maven 仓库来解决。 // Top-level build file where you can add configuration options com…...

关税冲击下,FBA国际物流企业如何靠智能拓客跑出增长“加速度”?
国际物流行业正迎来前所未有的增长机遇。据中研普华最新报告,2025年全球物流市场规模已突破6.27万亿美元,其中中国跨境物流市场预计达2.71万亿元。在全球化与数字化双轮驱动下,国际物流从“规模扩张”迈向“价值重构”。可以说,国…...

vue源代码采用的设计模式分解
No.大剑师精品GIS教程推荐0地图渲染基础- 【WebGL 教程】 - 【Canvas 教程】 - 【SVG 教程】 1Openlayers 【入门教程】 - 【源代码示例 300】 2Leaflet 【入门教程】 - 【源代码图文示例 150】 3MapboxGL【入门教程】 - 【源代码图文示例150】 4Cesium 【入门教程】…...
