Booth Encoding vs. Non-Booth Multipliers —— 穿透 DC 架构看乘法器的底层博弈
目录
🧭 前言
🌱 1. Non-Booth 乘法器的实现原理(也叫常规乘法器)
🔧 构建方式
✍️ 例子:4x4 Non-Booth 乘法器示意
🧱 硬件结构
✅ 特点总结
⚡ 2. Booth Encoding(布斯编码)乘法器
🧠 核心思想
✨ 举例:Radix-4 Booth(每两位一组)
📐 Booth 操作编码表(Radix-4)
🔧 硬件结构简图
✅ 特点总结
🏛️ 3. 在 Synopsys DC 中的使用策略
默认行为:
控制变量:
🧪 4. 如何验证 DC 选择了哪种乘法器?
方法一:Datapath Debug Log
方法二:report datapath structure
🎯 总结
🔚 延伸阅读
🧭 前言
在 datapath 构建阶段,乘法器是最重要的资源单元之一。
-
面积最大
-
时序瓶颈集中
-
能力决定系统吞吐
而 Synopsys Design Compiler (DC) 在构建乘法器结构时,核心决策之一就是:
❓是否采用 Booth Encoding?
❓如果不采用,怎么构建标准 non-Booth 乘法器?
这并不是一个简单选择,而是涉及多个维度的性能平衡。我们现在就从最底层原理开始:
🌱 1. Non-Booth 乘法器的实现原理(也叫常规乘法器)
🔧 构建方式
假设我们要计算两个无符号 4-bit 数相乘:
A = a3 a2 a1 a0
B = b3 b2 b1 b0
我们需要构建如下的部分积(partial products):
P0 = A * b0 --> A AND b0 (bitwise)
P1 = A * b1 << 1 --> A AND b1, shift left 1
P2 = A * b2 << 2 --> A AND b2, shift left 2
P3 = A * b3 << 3 --> A AND b3, shift left 3
最终的乘法结果是:
Result = P0 + P1 + P2 + P3
也就是说,n-bit × n-bit 的 non-Booth 乘法器需要生成 n 个部分积,然后加起来。
✍️ 例子:4x4 Non-Booth 乘法器示意
假设:
A = 4'b1101 (13)
B = 4'b1010 (10)
部分积:
P0 = 1101 & 0 = 0000
P1 = 1101 & 1 = 1101 << 1 = 11010
P2 = 1101 & 0 = 00000
P3 = 1101 & 1 = 1101 << 3 = 1101000
最终加起来:
Result = 0 + 11010 + 0 + 1101000 = 10000010 = 130
🧱 硬件结构
-
每一项
A * bi是 AND gates -
每个结果之间的加法使用 Carry-Save Adders(CSA)
-
最后一级使用 Carry-Propagate Adder(CPA)
非 Booth 的乘法器结构如下图逻辑(文字图):
A * b0 A * b1 A * b2 A * b3| | | |↓↓↓ ↓↓↓ ↓↓↓ ↓↓↓+----------+ +----------+ +----------+ +----------+| Shifter |-->| Shifter |-->| Shifter |-->| Shifter |+----------+ +----------+ +----------+ +----------+| | | |+--------------+--------------+---------------+|Multi-Adder Tree
✅ 特点总结
| 维度 | Non-Booth |
|---|---|
| 部分积数量 | n 个 |
| 面积 | 较大 |
| 延迟 | 多级加法器 |
| 符号位支持 | 需要扩展和修复 |
| 构建复杂度 | 中等 |
| 优点 | 实现简单,易调试 |
| 缺点 | 延迟长,乘法器大 |
⚡ 2. Booth Encoding(布斯编码)乘法器
Booth 是一种对乘法输入进行重编码的方式,可以减少部分积数量,进而降低延迟与面积。
🧠 核心思想
原始每个位做部分积太浪费。
Booth 把乘数 B 分组,比如两个一组,做符号差分编码,从而一组表示 3 种操作:
00 → 0
01 → +A
10 → -A
11 → 0(或特殊处理)
这样就可以跳过很多 "0" 操作,生成更少部分积。
✨ 举例:Radix-4 Booth(每两位一组)
假设:
B = b3 b2 b1 b0 = 1001 (9)
扩展为 b4=0
组合: (b4,b3,b2), (b2,b1,b0)
组1: 010 → +A
组2: 100 → -2A
所以只生成两组:
-
+A shift by 2
-
-2A shift by 0
相比非 Booth 的 4 个部分积,这里只用 2 个!
📐 Booth 操作编码表(Radix-4)
| 组值 (x2, x1, x0) | 操作 |
|---|---|
| 000 | 0 |
| 001 | +A |
| 010 | +A |
| 011 | +2A |
| 100 | -2A |
| 101 | -A |
| 110 | -A |
| 111 | 0 |
🔧 硬件结构简图
Booth Encoder → Booth Selector (0, +A, -A, +2A, -2A)↓Partial Products↓Adder Tree (Wallace or Dadda)
✅ 特点总结
| 维度 | Booth Encoding |
|---|---|
| 部分积数量 | 减半:n/2 |
| 延迟 | 更短 |
| 面积 | 较小(加法器更深但数量少) |
| 符号位支持 | 天然支持有符号数! |
| 实现复杂度 | 高(需要编码器+符号处理) |
| 优点 | 高性能,面积节省,支持负数 |
| 缺点 | 实现复杂,调试难,corner case 多 |
🏛️ 3. 在 Synopsys DC 中的使用策略
Design Compiler 会在 datapath 构建阶段自动选择:
默认行为:
-
有符号乘法 → Booth 优先
-
目标路径在 critical timing path → Booth 强制使用
-
常数乘法 → 不用 Booth,而是移位+加法特化
控制变量:
set_app_var datapath_enable_booth true
更精细控制:
set_app_var datapath_prefer_booth_multiplier true
set_app_var datapath_force_non_booth_multiplier false
你也可以用 constraint 引导:
set_multicycle_path -from A -to B -prefer_booth
🧪 4. 如何验证 DC 选择了哪种乘法器?
方法一:Datapath Debug Log
set_app_var datapath_debug_level 5
compile_design
会看到 log 中出现:
Info: Booth encoding applied to multiplier A * B
或
Warning: Fallback to non-Booth multiplier due to bit width mismatch
方法二:report datapath structure
report_datapath -design my_block
会显示 multiplier 类型和数量。
🎯 总结
| 比较维度 | Non-Booth | Booth |
|---|---|---|
| 部分积数量 | n | n/2 |
| 结构复杂度 | 中等 | 高(需要编码器) |
| 支持负数 | 手动符号扩展 | ✅天然支持 |
| 面积 | 较大 | 较小 |
| 延迟 | 多级累加 | 更少级数 |
| 调试 | 简单 | 较复杂(corner case 多) |
🧠 在时序收敛关键路径或 DSP 优化目标中,Booth 是你最好的朋友。
🛠 在低位宽、功耗优先或 RTL级测试场景中,Non-Booth 更易用、可控、可验证。
🔚 延伸阅读
📙《终结乘法瓶颈!带你彻底掌握 Booth Encoding 的秘密与架构》
📘《Non-Booth 乘法器的全解析:从 RTL 表达式到部分积压缩的完整路径》
相关文章:

Booth Encoding vs. Non-Booth Multipliers —— 穿透 DC 架构看乘法器的底层博弈
目录 🧭 前言 🌱 1. Non-Booth 乘法器的实现原理(也叫常规乘法器) 🔧 构建方式 ✍️ 例子:4x4 Non-Booth 乘法器示意 🧱 硬件结构 ✅ 特点总结 ⚡ 2. Booth Encoding(布斯编码…...
Midjourney-V7:支持参考图片头像或背景生成新保真图
Midjourney-V7重磅升级Omni Reference:全能图像参考神器!再也不用担心生成图片货不对版了! 就在上周,Midjourney发版它最新的V7版本:Omini Reference,提供了全方位图像参考功能,它可以参考你提…...

耀圣-气动带刮刀硬密封法兰球阀:攻克颗粒高粘度介质的自清洁 “利器”
气动带刮刀硬密封法兰球阀:攻克颗粒高粘度介质的自清洁 “利器” 在化工、矿业、食品加工等行业中,带颗粒高粘度介质、料浆及高腐蚀性介质的输送与控制一直是行业难题。普通阀门极易因介质附着、颗粒堆积导致卡阻失效,密封面磨损加剧&#x…...

Google云计算原理和应用之分布式锁服务Chubby
Chubby是Google设计的提供粗粒度锁服务的一个文件系统,它基于松耦合分布式系统,解决了分布的一致性问题。通过使用Chubby的锁服务,用户可以确保数据操作过程中的一致性。不过值得注意的是,这种锁只是一种建议性的锁(Advisory Lock)而不是强制性的锁,这种选择系统具有更大…...
SM2Utils NoSuchMethodError: org.bouncycastle.math.ec.ECFieldElement$Fp.<init
1,报错图示 2,报错原因: NoSuchMethodError 表示运行时找不到某个方法,通常是编译时依赖的库版本与运行时使用的库版本不一致。 错误中的 ECFieldElement$Fp. 构造函数参数为 (BigInteger, BigInteger),说明代码期望使…...

《100天精通Python——基础篇 2025 第16天:异常处理与调试机制详解》
目录 一、认识异常1.1 为什么要使用异常处理机制?1.2 语法错误1.3 异常错误1.4 如何解读错误信息 二、异常处理2.1 异常的捕获2.2 Python内置异常2.3 捕获多个异常2.4 raise语句与as子句2.5 使用traceback查看异常2.6 try…except…else语句2.7 try…except…finally语句--捕获…...

动态创建链表(头插法、尾插法)
今天我们来学习动态创建链表!!! 动态创建链表:分为头插法和尾插法 头插法(动态创建): 头插法就是让新节点变成头 代码如下 吐血了:这边有个非常重要的知识点,这边第三…...

利用混合磁共振成像 - 显微镜纤维束成像技术描绘结构连接组|文献速递-深度学习医疗AI最新文献
Title 题目 Imaging the structural connectome with hybrid MRI-microscopy tractography 利用混合磁共振成像 - 显微镜纤维束成像技术描绘结构连接组 01 文献速递介绍 通过多种模态绘制大脑结构能够增进我们对大脑功能、发育、衰老以及疾病的理解(汉森等人&am…...

安全监控之Linux核心资产SSH连接监测邮件
文章目录 一、引言二、邮箱设置三、脚本配置四、登录测试 一、引言 在某些特殊时期(如HVV)需要重点监控Linux核心资产SSH连接登录活动情况,实现ssh登录报警监控。其实实现方式并不难。 二、邮箱设置 在邮箱中需要启用“SMTP”协议…...
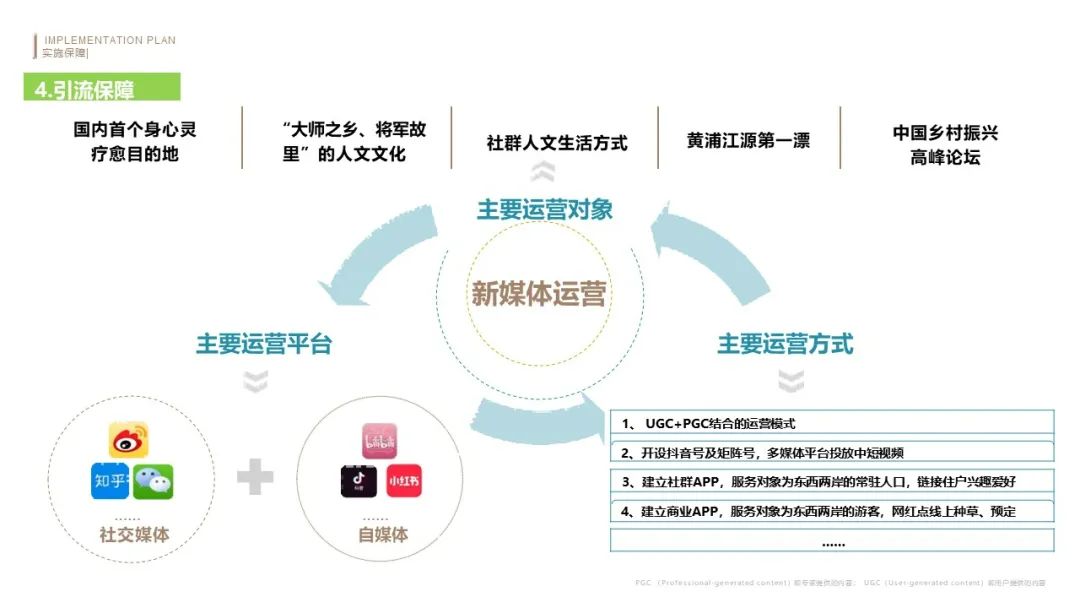
文旅田园康养小镇规划设计方案PPT(85页)
1. 项目背景与定位 背景:位于长三角经济圈,依托安吉丰富的自然与文化资源,旨在打造集康养、度假、文化体验于一体的综合小镇。 定位:成为浙北地区知名的康养旅游目的地,融合“一溪两岸”规划理念,实现全面…...
连接sql server数据库)
部署Superset BI(四)连接sql server数据库
sqlserver没有出现在Superset的连接可选菜单上,这一点让我奇怪。既然没有那就按着HANA的配置方式,照猫画虎。更奇怪的是安装好还不能出现,难道superset和微软有仇? --修改配置文件 rootNocobase:/usr/superset/superset# cd docke…...
【Linux操作系统】第一弹——Linux基础篇
文章目录 💡 一. Linux的基本常识🪔 1.1 linux网络连接三种方式🪔1.2 虚拟机的克隆🪔1.3 虚拟机的快照🪔1.4 虚拟机的迁移和删除🪔1.5 vmtools工具 💡二. Linux的目录结构🪔2.1 Linu…...

开源数字人框架 AWESOME - DIGITAL - HUMAN:技术革新与行业标杆价值剖析
一、项目核心价值:解锁数字人技术新境界 1. 技术普及:降低准入门槛,推动行业民主化 AWESOME - DIGITAL - HUMAN 项目犹如一场技术春雨,为数字人领域带来了普惠甘霖。它集成了 ASR、LLM、TTS 等关键能力,并提供模块化扩展接口,将原本复杂高深的数字人开发流程,转化为一…...

Mysql--基础知识点--91.1--慢查询日志
MySQL 慢查询日志是优化数据库性能的核心工具之一,用于记录执行时间超过指定阈值的 SQL 语句。以下是详细使用指南: 一、配置慢查询日志 1. 临时启用(重启后失效) -- 启用慢查询日志(立即生效) SET GLOBA…...
(父传子)- props实现)
react-12父子组件间的数据传递(子传父)(父传子)- props实现
1.子组件调用父组件的函数并传递数据(子传父) 1.1父组件 import React, { Component } from react; import ChildComponent from ./ChildComponent;class ParentComponent extends Component {constructor(props) {super(props);this.state {items: […...

vue3: pdf.js 2.16.105 using typescript
npm create vite vuepdfpreview //创建项目npm install vue-pdf-embed npm install vue3-pdfjs npm install pdfjs-dist2.16.105 <!--* |~~~~~~~|* | |* | |…...

从 MDM 到 Data Fabric:下一代数据架构如何释放 AI 潜能
从 MDM 到 Data Fabric:下一代数据架构如何释放 AI 潜能 —— 传统治理与新兴架构的范式变革与协同进化 引言:AI 规模化落地的数据困境 在人工智能技术快速发展的今天,企业对 AI 的期望已从 “单点实验” 转向 “规模化落地”。然而&#…...

【软件测试】测试用例的设计方法
目录 一、基于需求进行测试用例的设计 1.1 功能需求测试分析 二、黑盒测试用例设计方法 2.1 等价类划分法(解决穷举) 2.1.1 等价类设计步骤 2.1.2 等价类划分法案例 2.1.2.1 验证 QQ 账号的合法性 2.1.2.2 验证某城市电话号码的正确性 2.1.3 适用场景 2.2 边界值分析…...

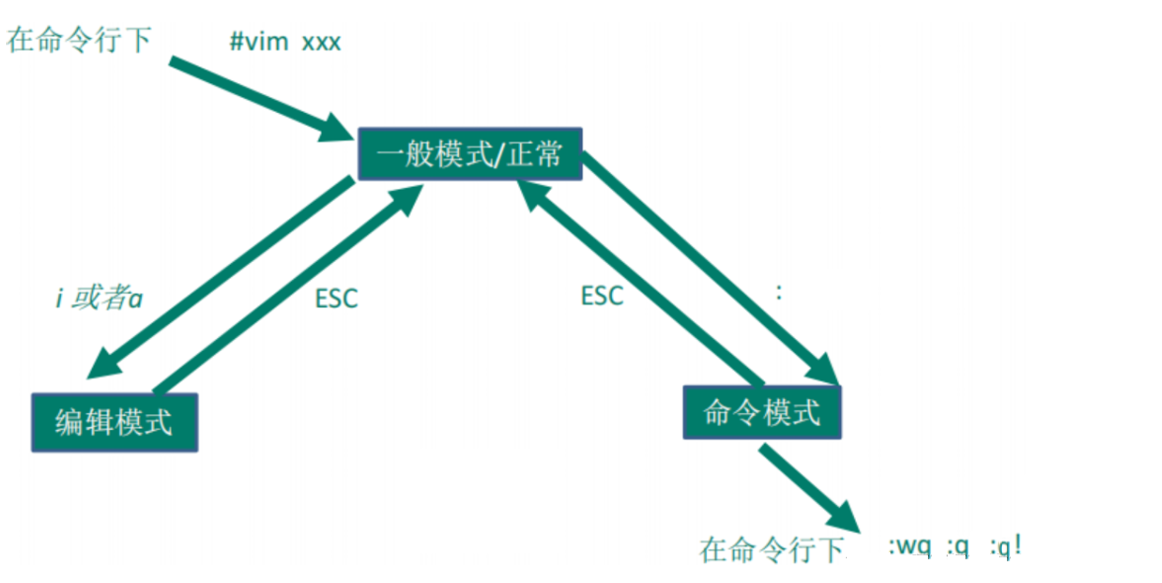
Vim 命令从头学习记录
学习链接:eleon-vim基础教程 Vim - 基础翻屏操作 光标移动:hjkl 20j 向下移动20行,w 向后移动一个字符,b 向前移动一个字符。 Ctrl u 向上翻半页 UP Ctrl d 向下翻半页 Down Ctrl f 向下翻整页 Forward Ctrl b 向上翻整页 …...

初等数论--欧拉函数及其性质
1. 定义 ϕ ( n ) \phi(n) ϕ(n)在数论中代表欧拉函数, 它的值为小于等于 n n n且与 n n n互质的正整数的个数。 2. 性质 若 p p p为质数,则 ϕ ( p ) p − 1 \phi(p) p-1 ϕ(p)p−1; 除了自身以外全都互质。 若 p p p为质数,则 ϕ ( p…...

Java、javax 和 Jakarta有什么区别?
在 Java 开发中,我们经常会看到 java、javax 和 jakarta 这些包名前缀。本文将详细介绍这三个命名空间的含义、发展历程以及它们之间的关系,帮助你更好地理解 Java 生态系统。 一、Java:核心 API 的基础 ✅ 含义: java 是 Java 标准库的核心包名。所有以 java. 开头的类构…...

Java中的控制流语句:if、switch、for、foreach、while、do-while
Java中的控制流语句 Java中的控制流语句用于控制程序执行的流程。这些语句包括条件判断语句和循环语句。本文将详细介绍Java中的 if、switch、for、foreach、while、do-while控制流语句。 一、条件判断语句 1. if语句 if语句根据表达式的真假来决定是否执行代码块。 int x…...

GStreamer开发笔记(三):测试gstreamer/v4l2+sdl2/v4l2+QtOpengl打摄像头延迟和内存
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://blog.csdn.net/qq21497936/article/details/147714800 长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、O…...

科技成果鉴定测试有哪些内容?又有什么作用?
科技成果鉴定测试是评价科技成果质量和水平的方法之一,通过测试,可以对科技成果的技术优劣进行评估,从而为科技创新提供参考和指导。 一、科技成果鉴定测试的内容 1.技术评审:通过技术专家对项目进行详细的技术分析ÿ…...

基于Spring Boot + Vue 项目中引入deepseek方法
准备工作 在开始调用 DeepSeek API 之前,你需要完成以下准备工作: 1.访问 DeepSeek 官网,注册一个账号。 2.获取 API 密钥:登录 DeepSeek 平台,进入 API 管理 页面。创建一个新的 API 密钥(API Key&#x…...

A2A与MCP定义下,User,Agent,api(tool)间的交互流程图
官方图: 流程图: #mermaid-svg-2smjE8VYydjtLH0p {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-2smjE8VYydjtLH0p .error-icon{fill:#552222;}#mermaid-svg-2smjE8VYydjtLH0p .error-tex…...

蓝桥杯2025年第十六届省赛真题-水质检测
C语言代码: #include <stdio.h> #include <string.h>#define MAX_LEN 1000000int main() {char a[MAX_LEN 1], b[MAX_LEN 1];// 使用 scanf 读取字符数组scanf("%s", a);scanf("%s", b);int ans 0;int pre -1;int state -1;i…...

机器学习第二讲:对比传统编程:解决复杂规则场景
机器学习第二讲:对比传统编程:解决复杂规则场景 资料取自《零基础学机器学习》。 查看总目录:学习大纲 关于DeepSeek本地部署指南可以看下我之前写的文章:DeepSeek R1本地与线上满血版部署:超详细手把手指南 一、场景…...

[Windows] 东芝存储诊断工具1.30.8920(20170601)
[Windows] 东芝存储诊断工具 链接:https://pan.xunlei.com/s/VOPpMjGdWZOLceIjxLNiIsIEA1?pwduute# 适用型号 东芝消费类存储产品: 外置硬盘:Canvio 系列 内置硬盘:HDW****(E300 / N300 / P300 / S300 / V300 / X30…...
)
[蓝桥杯 2025 省 B] 水质检测(暴力 )
暴力暴力 菜鸟第一次写题解,多多包涵!!! 这个题目的数据量很小,所以没必要去使用bfs,直接分情况讨论即可 一共两排数据,我们使用贪心的思想,只需要实现从左往右的过程中每个检测器相互连接即…...
