红黑树删除的实现与四种情况的证明
🧭 学习重点
- 删除节点的三种情况
- 红黑树如何恢复性质
- 四种修复情况
- 完整可运行的 C++ 实现
一、红黑树删除的基础理解
红黑树删除比插入复杂得多,因为:
- 删除的是黑节点可能会破坏“从根到叶子黑节点数相等”的性质。
- 删除红节点无需修复,直接删。
- 删除黑节点,要么借黑色、要么旋转重构。
二、删除节点的三种基本情况(和 BST 类似)
- 无子节点(叶子节点):直接删。
- 有一个子节点:用子节点替代。
- 有两个子节点:找到中序后继,用其值替换被删节点,然后删除后继。
注意:红黑树中处理的是“颜色破坏”,不是结构本身。
三、红黑树删除修复目标
- 恢复五大性质(尤其是黑高一致性)
- 使用双黑节点表示“临时多了一层黑色”
- 四种修复方式:兄弟红、兄弟黑侄红、兄弟黑侄黑、旋转变色
四、四种删除修复情况(核心)
设 x 为“被提上来”的节点(可能是 NIL)
✅ Case 1:x 的兄弟是红色
P(B) S(B)
/ \ => / \
x(B) S(R) P(R) Sr(B)
/ \ / \
Sl Sr x(B) Sl- 父变红,兄变黑,左旋父节点,变成 Case 2~4。
✅ Case 2:x 的兄弟是黑色,且两个侄子都是黑色
P(?)
/ \
x(B) S(B)
/ \
B B- 把
S变红,x = p,向上传递双黑
✅ Case 3:兄弟黑,近侄子红,远侄子黑
P(?)
/ \
x(B) S(B)
/
R- 先右旋
S,再变成 Case 4
✅ Case 4:兄弟黑,远侄子红
P(?)
/ \
x(B) S(B)
\
R- 左旋
p,交换p和s颜色,把远侄子设为黑,修复完毕
五、完整 C++ 实现:红黑树删除
我们先定义红黑树结构(含旋转、插入、删除等):
✅ 树结构和节点定义
#include <iostream>
using namespace std;enum Color { RED, BLACK };struct Node {
int val;
Color color;
Node *left, *right, *parent;Node(int val): val(val), color(RED), left(nullptr), right(nullptr), parent(nullptr) {}
};✅ 左旋操作
void leftRotate(Node*& root, Node* x) {Node* y = x->right;x->right = y->left;if (y->left) y->left->parent = x;y->parent = x->parent;if (!x->parent) root = y;else if (x == x->parent->left) x->parent->left = y;else x->parent->right = y;y->left = x;x->parent = y;
}✅ 右旋操作
void rightRotate(Node*& root, Node* y) {Node* x = y->left;y->left = x->right;if (x->right) x->right->parent = y;x->parent = y->parent;if (!y->parent) root = x;else if (y == y->parent->left) y->parent->left = x;else y->parent->right = x;x->right = y;y->parent = x;
}✅ 找到最小节点(用于后继替换)
Node* minimum(Node* node) {while (node->left) node = node->left;return node;
}✅ 删除修复函数
void deleteFixUp(Node*& root, Node* x) {while (x != root && (!x || x->color == BLACK)) {if (x == x->parent->left) {Node* w = x->parent->right;if (w->color == RED) {w->color = BLACK;x->parent->color = RED;leftRotate(root, x->parent);w = x->parent->right;}if ((!w->left || w->left->color == BLACK) &&(!w->right || w->right->color == BLACK)) {w->color = RED;x = x->parent;} else {if (!w->right || w->right->color == BLACK) {if (w->left) w->left->color = BLACK;w->color = RED;rightRotate(root, w);w = x->parent->right;}w->color = x->parent->color;x->parent->color = BLACK;if (w->right) w->right->color = BLACK;leftRotate(root, x->parent);x = root;}} else {// 对称处理Node* w = x->parent->left;if (w->color == RED) {w->color = BLACK;x->parent->color = RED;rightRotate(root, x->parent);w = x->parent->left;}if ((!w->left || w->left->color == BLACK) &&(!w->right || w->right->color == BLACK)) {w->color = RED;x = x->parent;} else {if (!w->left || w->left->color == BLACK) {if (w->right) w->right->color = BLACK;w->color = RED;leftRotate(root, w);w = x->parent->left;}w->color = x->parent->color;x->parent->color = BLACK;if (w->left) w->left->color = BLACK;rightRotate(root, x->parent);x = root;}}}if (x) x->color = BLACK;
}✅ 删除操作主函数
void rbDelete(Node*& root, Node* z) {Node* y = z;Node* x;Color yOriginalColor = y->color;if (!z->left) {x = z->right;transplant(root, z, z->right);} else if (!z->right) {x = z->left;transplant(root, z, z->left);} else {y = minimum(z->right);yOriginalColor = y->color;x = y->right;if (y->parent == z) {if (x) x->parent = y;} else {transplant(root, y, y->right);y->right = z->right;y->right->parent = y;}transplant(root, z, y);y->left = z->left;y->left->parent = y;y->color = z->color;}if (yOriginalColor == BLACK)deleteFixUp(root, x);
}✅ 替换子树辅助函数
void transplant(Node*& root, Node* u, Node* v) {if (!u->parent) root = v;else if (u == u->parent->left) u->parent->left = v;else u->parent->right = v;if (v) v->parent = u->parent;
}六、总结与练习建议
- 删除是红黑树最复杂操作,逻辑较多但结构稳定
- 建议多画图分析每种情况
- 自己实现一棵树,从插入到删除,打印中序遍历验证
相关文章:

红黑树删除的实现与四种情况的证明
🧭 学习重点 删除节点的三种情况红黑树如何恢复性质四种修复情况完整可运行的 C 实现 一、红黑树删除的基础理解 红黑树删除比插入复杂得多,因为: 删除的是黑节点可能会破坏“从根到叶子黑节点数相等”的性质。删除红节点无需修复…...

【Spring AI 实战】基于 Docker Model Runner 构建本地化 AI 聊天服务:从配置到函数调用全解析
【Spring AI 实战】基于 Docker Model Runner 构建本地化 AI 聊天服务:从配置到函数调用全解析 前沿:本地化 AI 推理的新范式 随着大语言模型(LLM)应用的普及,本地化部署与灵活扩展成为企业级 AI 开发的核心需求。Do…...

前台--Android开发
在 Android 开发中,“前台(Foreground)” 是一个非常重要的概念,它用于描述当前用户正在与之交互的组件或应用状态。理解“前台”的含义有助于更好地管理资源、生命周期和用户体验。 ✅ 一、什么是前台? 简单定义&…...

跨境电商生死局:动态IP如何重塑数据生态与运营效率
凌晨三点的深圳跨境电商产业园,某品牌独立站运营总监李明(化名)正盯着突然中断的广告投放系统。后台日志显示,过去24小时内遭遇了17次IP封禁,直接导致黑五促销期间损失23%的预期流量。这并非个案——2023年跨境电商行业…...

springboot3+vue3融合项目实战-大事件文章管理系统-更新用户信息
在一下三个代码处进行修改 在UserController里面增加uadate方法 PutMapping ("/update")public Result update(RequestBody Validated User user){userService.update(user);return Result.success();}在userservice中增加update方法 void update(User user); 然…...
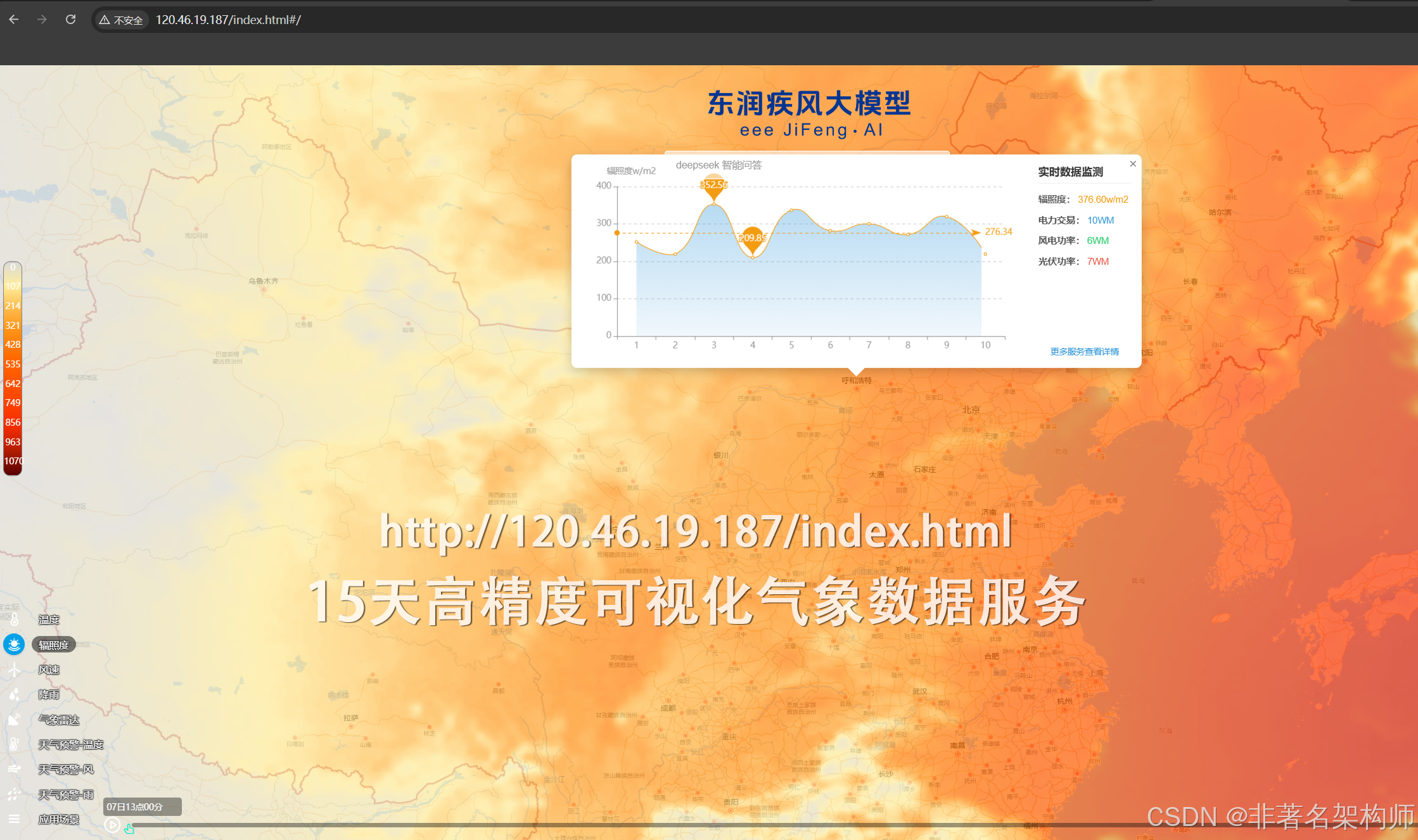
气象大模型光伏功率预测中的应用:从短期,超短期,中长期的实现与开源代码详解
1. 引言 光伏功率预测对于电力系统调度、能源管理和电网稳定性至关重要。随着深度学习技术的发展,大模型(如Transformer、LSTM等)在时间序列预测领域展现出强大能力。本文将详细介绍基于大模型的光伏功率预测方法,涵盖短期(1-6小时)、超短期(15分钟-1小时)和中长期(1天-1周…...

深度学习:智能车牌识别系统(python)
这是一个基于opencv的智能车牌识别系统,有GUI界面。程序能自动识别图片中的车牌号码,并支持中文和英文字符识别,支持选择本地图片文件,支持多种图片格式(jpg、jpeg、png、bmp、gif)。 下面,我将按模块功能对代码进行分段说明: 1. 导入模块部分 import tkinter as tk…...

[杂谈随感-13]: 人的睡眠,如何布置床的位置比较有安全?感?
睡眠环境中的床位布置直接影响心理安全感与睡眠质量,需从空间防御性、人体感知机制及环境心理学多维度综合设计。 以下基于科学原理与实践案例,系统解析床位布置的核心策略: 一、空间防御性布局:构建心理安全边界 背靠实体墙&a…...

DNS服务实验
该文章将介绍DNS服务的正向和反向解析实验、主从实验、转发服务器实验以及Web解析实验 正向解析实验:将域名解析为对应的IP地址 反向解析实验:将IP地址解析为对应的域名 主从实验:主服务器区域数据文件发送给从服务器,从服务器…...

visual studio 2015 安装闪退问题
参考链接: VS2012安装时启动界面一闪而过问题解决办法 visual studio 2015 安装闪退问题...

C语言复习--动态内存管理
下面我们来看C语言中的动态内存管理,在之后的数据结构中会运用到C语言中的指针,结构体和动态内存管理,所以这部分还是比较重要的.下面进入正题. 为什么要有动态内存分配 但是上面的两种方式开辟的内存的大小都是固定的.数组也是,在数组开辟之前一定要确定好数组大小,并且数组开…...

Python实例题:Python协程详解公开课
目录 Python实例题 题目 课程目标 课程内容规划 1. 课程开场(5 分钟) 2. 基础概念讲解(15 分钟) 并发与并行: 线程与进程: 3. Python 协程的实现方式(20 分钟) 生成器实现…...

青藏高原七大河流源区径流深、蒸散发数据集(TPRED)
时间分辨率 月空间分辨率 1km - 10km共享方式 开放获取数据大小 83.27 MB数据时间范围 1998-07-01 — 2017-12-31元数据更新时间 2024-07-22 数据集摘要 通过构建耦合积雪、冻土、冰川等冰冻圈水文物理过程的WEB-DHM模型(Water and Energy Budget-based Distribute…...

[学习]RTKLib详解:rtksvr.c与streamsvr.c
本文是 RTKLlib详解 系列文章的一篇,目前该系列文章还在持续总结写作中,以发表的如下,有兴趣的可以翻阅。 [学习] RTKlib详解:功能、工具与源码结构解析 [学习]RTKLib详解:pntpos.c与postpos.c [学习]RTKLib详解&…...

Docker使用小结
概念 镜像( Image ) :相当于一个 root 文件系统;镜像构建时,分层存储、层层构建;容器( Container ) :镜像是静态的定义,容器是镜像运行时的实体;…...

串口屏调试 1.0
http://wiki.tjc1688.com 先把商家的链接贴过来 淘晶驰T1系列3.2寸串口屏tft液晶屏显示屏HMI触摸屏超12864液晶屏 这是主包的型号 打开这个玩意 有十个基本的功能区 新建工程 在界面的右边,指令一定要写在page前面,这里的波特率等等什么的都可以…...

windows 环境下 python环境安装与配置
运行环境安装 第一步安装包下载 python开发工具安装包下载官网: https://www.python.org/ 根据自己的实际需求选择。 这里记录了各个版本的区别和差异。根据区别和差异选择适合自己的版本。 Windows Installer和Windows embeddable package是两种不同的软件包类…...

浅谈装饰模式
一、前言 hello大家好,本次打算简单聊一下装饰者模式,其实写有关设计模式的内容还是蛮有挑战性的,首先呢就是小永哥实力有限担心说不明白,其次设计模式是为了解决某些问题场景,在当前技术生态圈如此完善的情况下&#…...

LeetCode 270:在二叉搜索树中寻找最接近的值(Swift 实战解析)
文章目录 摘要描述题解答案题解代码分析示例测试及结果时间复杂度空间复杂度总结 摘要 在日常开发中,我们经常需要在一组有序的数据中快速找到最接近某个目标值的元素。LeetCode 第 270 题“Closest Binary Search Tree Value”正是这样一个问题。本文将深入解析该…...

WPF 3D图形编程核心技术解析
一、三维坐标系系统 WPF采用右手坐标系系统,空间定位遵循: X 轴 → 右 Y 轴 → 上 Z 轴 → 观察方向 X轴 \rightarrow 右\quad Y轴 \rightarrow 上\quad Z轴 \rightarrow 观察方向 X轴→右Y轴→上Z轴→观察方向 三维坐标值表示为 ( x , y , z ) (x, y,…...

分布式锁原理
1.锁是什么 一个线程拿到锁,另一个线程就拿不到,满足互斥性。 2.Redis的setnx实现 加锁后解锁,但是要先判断是否是当前线程持有的锁,只能释放本线程的锁。 先判断后释放,两步操作Lua实现原子性 3.为什么要给锁加过期…...

暗物质卯引力挂载技术
1、物体质量以及其所受到的引力约束(暗物质压力差) 自然界的所有物体,其本身都是没有质量的。我们所理解的质量,其实是物体球周空间的暗物质对物体的挤压,压力差。 对于宇宙空间中的单个星球而言,它的球周各处压力是相同的,所以,它处于平衡状态,漂浮在宇宙中。 对于星…...

实现三个采集板数据传送到一个显示屏的方案
实现三个采集板数据传送到一个显示屏的方案 要实现三个相同采集板的数据都传送到一个显示屏上,可行的方案: 方案:串行通信(推荐) 硬件连接: 使用RS485总线连接(适合较长距离)或使用…...

comfyui 如何优雅的从Hugging Face 下载模型,文件夹
如下图所示 使用git 下载整个仓库然后把需要的放到对应的位置...

通过user-agent来源判断阻止爬虫访问网站,并防止生成[ error ] NULL日志
一、TP5.0通过行为(Behavior)拦截爬虫并避免生成 [ error ] NULL 错误日志 1. 创建行为类(拦截爬虫) 在 application/common/behavior 目录下新建BlockBot.php ,用于识别并拦截爬虫请求: <?php name…...

动态规划法:爬楼梯
假如你现在爬楼梯,需要n阶才能到达楼顶,每次可以爬1或2 台阶,你有多少中不同的方法可以爬到楼顶。 例如: 输入:n2 输出:2 //有两种方法可以到达楼顶,1阶1阶,2阶。 输入&…...

IBM BAW(原BPM升级版)使用教程第七讲
续前篇! 一、团队 在 IBM Business Automation Workflow (BAW) 中,团队(Team) 是流程管理的关键部分,用于定义参与某个流程的用户、角色、组以及服务等。在团队配置中,有许多重要概念,特别是 …...

【论文阅读】Efficient and secure federated learning against backdoor attacks
Efficient and secure federated learning against backdoor attacks -- 高效且安全的可抵御后门攻击的联邦学习 论文来源问题背景TLDR系统及威胁模型实体威胁模型 方法展开服务器初始化本地更新本地压缩高斯噪声与自适应扰动聚合与解压缩总体算法 总结优点缺点 论文来源 名称…...

Java中的代理机制
目录 什么叫代理 静态代理 优缺点 优点: 缺点: 动态代理 JDK动态代理 核心类 JDK动态代理的实现 步骤 示例 特点 CGLIB动态代理 代理机制对比 总结 什么叫代理 代理模式是一种比较好理解的设计模式。简单来说就是我们使用代理对象来代替…...

Kotlin扩展函数提升Android开发效率
在Android开发中,Kotlin的扩展函数(Extension Functions)犹如一把神奇的瑞士军刀,它能显著提升代码简洁性和开发效率。以下是通过实战案例展示的扩展函数魔法手册: 一、扩展函数基础原理 // 给View添加渐显动画扩展 f…...
