详解SLAM中的李群和李代数(中)
1 概述
在上一篇文章《详解SLAM中的李群和李代数(上)》中,我们已经通过对李群求导引出了李代数。在这篇文章中,我们就系统总结一下李代数的相关知识。
2 李代数
2.1 定义
李代数是一个向量空间 g \mathfrak{g} g与一个二元运算的组合。其中的二元运算称为李括号(Lie bracket),记为 [ ⋅ , ⋅ ] : g × g → g [\cdot,\cdot]: \mathfrak{g} \times \mathfrak{g} \rightarrow \mathfrak{g} [⋅,⋅]:g×g→g。在这个公式中:
- [ ⋅ , ⋅ ] [\cdot,\cdot] [⋅,⋅]是一个二元运算符,表示两个元素之间的某种“乘法”操作。当然它不是普通的乘法,常见的运算操作是向量叉乘 × \times × 或矩阵的换位子 [ A , B ] = A B − B A [A,B] = AB - BA [A,B]=AB−BA。
- g \mathfrak{g} g 是李代数的集合(通常是一个向量空间), g × g \mathfrak{g} \times\mathfrak{g} g×g 就是说我们要从这个集合里取两个元素做运算, → g \rightarrow \mathfrak{g} →g表示运算的结果仍然属于同一个集合 g \mathfrak{g} g。也就是说李括号运算把两个李代数中的元素变成另一个李代数中的元素。其实就是封闭性的意思。
李代数需要满足以下三个公理:
-
双线性:对于所有 x , y , z ∈ g x, y, z \in \mathfrak{g} x,y,z∈g和所有标量 a , b a, b a,b,有:
[ a x + b y , z ] = a [ x , z ] + b [ y , z ] , [ z , a x + b y ] = a [ z , x ] + b [ z , y ] [ax + by, z] = a[x, z] + b[y, z],\quad [z, ax + by] = a[z, x] + b[z, y] [ax+by,z]=a[x,z]+b[y,z],[z,ax+by]=a[z,x]+b[z,y] -
反对称性:对于所有 x , y ∈ g x, y \in \mathfrak{g} x,y∈g,有:
[ x , y ] = − [ y , x ] [x, y] = -[y, x] [x,y]=−[y,x]特别地,这意味着 [ x , x ] = 0 [x,x]=0 [x,x]=0。
-
雅可比恒等式:对于所有 x , y , z ∈ g x, y, z \in \mathfrak{g} x,y,z∈g,有:
[ x , [ y , z ] ] + [ y , [ z , x ] ] + [ z , [ x , y ] ] = 0 [x,[y,z]] + [y,[z,x]] + [z,[x,y]] = 0 [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0
如果是第一次接触到李代数这个概念,这三个特性公理并不太好理解,因为缺少实际的使用场景。但是这里还是举一个例子来加深印象。例如,三维向量空间 R 3 \mathbb{R}^3 R3和其上定义的叉乘 × \times ×构成了一个李代数 ( R 3 , × ) (\mathbb{R}^3, \times) (R3,×),李括号为 [ u , v ] = u × v [\boldsymbol{u}, \boldsymbol{v}] = \boldsymbol{u} \times \boldsymbol{v} [u,v]=u×v。它符合李代数的三个公理:
-
双线性:假设有向量 u = ( 1 , 0 , 0 ) \boldsymbol{u} = (1, 0, 0) u=(1,0,0), v = ( 0 , 1 , 0 ) \boldsymbol{v} = (0, 1, 0) v=(0,1,0), w = ( 0 , 0 , 1 ) \boldsymbol{w} = (0, 0, 1) w=(0,0,1),以及标量 a = 2 a=2 a=2, b = 3 b=3 b=3。
- 计算 [ a u + b v , w ] [a\boldsymbol{u} + b\boldsymbol{v}, \boldsymbol{w}] [au+bv,w]:
[ ( 2 , 0 , 0 ) + ( 0 , 3 , 0 ) , ( 0 , 0 , 1 ) ] = [ ( 2 , 3 , 0 ) , ( 0 , 0 , 1 ) ] = ( 3 , − 2 , 0 ) [(2, 0, 0) + (0, 3, 0), (0, 0, 1)] = [(2, 3, 0), (0, 0, 1)] = (3, -2, 0) [(2,0,0)+(0,3,0),(0,0,1)]=[(2,3,0),(0,0,1)]=(3,−2,0) - 计算 a [ u , w ] + b [ v , w ] a[\boldsymbol{u}, \boldsymbol{w}] + b[\boldsymbol{v}, \boldsymbol{w}] a[u,w]+b[v,w]:
2 [ ( 1 , 0 , 0 ) , ( 0 , 0 , 1 ) ] + 3 [ ( 0 , 1 , 0 ) , ( 0 , 0 , 1 ) ] = 2 ( 0 , 1 , 0 ) + 3 ( − 1 , 0 , 0 ) = ( 3 , − 2 , 0 ) 2[(1, 0, 0), (0, 0, 1)] + 3[(0, 1, 0), (0, 0, 1)] = 2(0, 1, 0) + 3(-1, 0, 0) = (3, -2, 0) 2[(1,0,0),(0,0,1)]+3[(0,1,0),(0,0,1)]=2(0,1,0)+3(−1,0,0)=(3,−2,0)
两式结果相等,符合双线性公理。
- 计算 [ a u + b v , w ] [a\boldsymbol{u} + b\boldsymbol{v}, \boldsymbol{w}] [au+bv,w]:
-
反对称性:假设 u = ( 1 , 0 , 0 ) \boldsymbol{u} = (1, 0, 0) u=(1,0,0)和 v = ( 0 , 1 , 0 ) \boldsymbol{v} = (0, 1, 0) v=(0,1,0)。
- 计算 [ u , v ] [\boldsymbol{u}, \boldsymbol{v}] [u,v]:
( 1 , 0 , 0 ) × ( 0 , 1 , 0 ) = ( 0 , 0 , 1 ) (1, 0, 0) \times (0, 1, 0) = (0, 0, 1) (1,0,0)×(0,1,0)=(0,0,1) - 计算 [ v , u ] [\boldsymbol{v}, \boldsymbol{u}] [v,u]:
( 0 , 1 , 0 ) × ( 1 , 0 , 0 ) = ( 0 , 0 , − 1 ) (0, 1, 0) \times (1, 0, 0) = (0, 0, -1) (0,1,0)×(1,0,0)=(0,0,−1)
可以看到 [ u , v ] = − ( [ v , u ] ) [\boldsymbol{u}, \boldsymbol{v}] = -( [\boldsymbol{v}, \boldsymbol{u}] ) [u,v]=−([v,u]),这符合反对称性。
- 计算 [ u , v ] [\boldsymbol{u}, \boldsymbol{v}] [u,v]:
-
雅可比恒等式:假设 u = ( 1 , 0 , 0 ) \boldsymbol{u} = (1, 0, 0) u=(1,0,0), v = ( 0 , 1 , 0 ) \boldsymbol{v} = (0, 1, 0) v=(0,1,0), w = ( 0 , 0 , 1 ) \boldsymbol{w} = (0, 0, 1) w=(0,0,1)。
- 计算 [ u , [ v , w ] ] [\boldsymbol{u}, [\boldsymbol{v}, \boldsymbol{w}]] [u,[v,w]]:
[ u , ( 0 , 1 , 0 ) × ( 0 , 0 , 1 ) ] = [ ( 1 , 0 , 0 ) , ( 1 , 0 , 0 ) ] = ( 0 , 0 , 0 ) [\boldsymbol{u}, (0, 1, 0) \times (0, 0, 1)] = [(1, 0, 0), (1, 0, 0)] = (0, 0, 0) [u,(0,1,0)×(0,0,1)]=[(1,0,0),(1,0,0)]=(0,0,0) - 计算 [ v , [ w , u ] ] [\boldsymbol{v}, [\boldsymbol{w}, \boldsymbol{u}]] [v,[w,u]]:
[ v , ( 0 , 0 , 1 ) × ( 1 , 0 , 0 ) ] = [ ( 0 , 1 , 0 ) , ( 0 , 1 , 0 ) ] = ( 0 , 0 , 0 ) [\boldsymbol{v}, (0, 0, 1) \times (1, 0, 0)] = [(0, 1, 0), (0, 1, 0)] = (0, 0, 0) [v,(0,0,1)×(1,0,0)]=[(0,1,0),(0,1,0)]=(0,0,0) - 计算 [ w , [ u , v ] ] [\boldsymbol{w}, [\boldsymbol{u}, \boldsymbol{v}]] [w,[u,v]]:
[ w , ( 1 , 0 , 0 ) × ( 0 , 1 , 0 ) ] = [ ( 0 , 0 , 1 ) , ( 0 , 0 , 1 ) ] = ( 0 , 0 , 0 ) [\boldsymbol{w}, (1, 0, 0) \times (0, 1, 0)] = [(0, 0, 1), (0, 0, 1)] = (0, 0, 0) [w,(1,0,0)×(0,1,0)]=[(0,0,1),(0,0,1)]=(0,0,0)
因此,
[ u , [ v , w ] ] + [ v , [ w , u ] ] + [ w , [ u , v ] ] = ( 0 , 0 , 0 ) + ( 0 , 0 , 0 ) + ( 0 , 0 , 0 ) = ( 0 , 0 , 0 ) [\boldsymbol{u}, [\boldsymbol{v}, \boldsymbol{w}]] + [\boldsymbol{v}, [\boldsymbol{w}, \boldsymbol{u}]] + [\boldsymbol{w}, [\boldsymbol{u}, \boldsymbol{v}]] = (0, 0, 0) + (0, 0, 0) + (0, 0, 0) = (0, 0, 0) [u,[v,w]]+[v,[w,u]]+[w,[u,v]]=(0,0,0)+(0,0,0)+(0,0,0)=(0,0,0)这验证了雅可比恒等式成立。
- 计算 [ u , [ v , w ] ] [\boldsymbol{u}, [\boldsymbol{v}, \boldsymbol{w}]] [u,[v,w]]:
注意,笔者这里对于李代数的定义与《视觉SLAM十四讲》上的定义略有不同,但是表达的实际的含义是一样的,读者可以自行体会。
2.2 李代数 s o ( 3 ) \mathfrak{so}(3) so(3)
在上一篇文章《详解SLAM中的李群和李代数(上)》中笔者实现了对特殊正交群 S O ( 3 ) SO(3) SO(3)的求导:
R ( t ) = exp ( [ ω ( t ) ] × t ) R(t) = \exp([\boldsymbol{\omega}(t)]_\times t) R(t)=exp([ω(t)]×t)
其中 exp \exp exp表示矩阵指数运算, ω ( t ) \boldsymbol{\omega}(t) ω(t)是表达旋转矩阵的旋转向量, [ ω ( t ) ] × [\boldsymbol{\omega}(t)]_{\times} [ω(t)]×是其对应的反对称矩阵。去掉用于求导的自变量 t t t,那么可以定义 S O ( 3 ) SO(3) SO(3)对应的李代数是:
s o ( 3 ) = { [ ω ] × ∈ R 3 × 3 ∣ ω ∈ R 3 } \mathfrak{so}(3) = \left\{ [\boldsymbol{\omega}]_\times \in \mathbb{R}^{3 \times 3} \mid {\omega} \in \mathbb{R}^3 \right\} so(3)={[ω]×∈R3×3∣ω∈R3}
也就是说, s o ( 3 ) \mathfrak{so}(3) so(3)是所有实 3 × 3 3\times 3 3×3反对称矩阵构成的集合,对应的李括号是两个元素之间的换位子(commutator)。
2.3 s o ( 3 ) \mathfrak{so}(3) so(3)的李括号
这里的李括号也就是换位子运算具体定义是:对于任意 X , Y ∈ s o ( 3 ) X, Y \in \mathfrak{so}(3) X,Y∈so(3),有:
[ X , Y ] = X Y − Y X [X, Y] = XY - YX [X,Y]=XY−YX
例如,在 s o ( 3 ) \mathfrak{so}(3) so(3)中,如果 X = [ ω 1 ] × X = [\boldsymbol{\omega}_1]_\times X=[ω1]×和 Y = [ ω 2 ] × Y = [\boldsymbol{\omega}_2]_\times Y=[ω2]×,则:
[ [ ω 1 ] × , [ ω 2 ] × ] = [ ω 1 ] × [ ω 2 ] × − [ ω 2 ] × [ ω 1 ] × [[\boldsymbol{\omega}_1]_\times, [\boldsymbol{\omega}_2]_\times] = [\boldsymbol{\omega}_1]_\times [\boldsymbol{\omega}_2]_\times - [\boldsymbol{\omega}_2]_\times [\boldsymbol{\omega}_1]_\times [[ω1]×,[ω2]×]=[ω1]×[ω2]×−[ω2]×[ω1]×
这个表达式的结果仍然是一个反对称矩阵,并且它对应于向量 ω 1 × ω 2 \boldsymbol{\omega}_1 \times \boldsymbol{\omega}_2 ω1×ω2的反对称矩阵,即:
[ [ ω 1 ] × , [ ω 2 ] × ] = [ ω 1 × ω 2 ] × [[\boldsymbol{\omega}_1]_\times, [\boldsymbol{\omega}_2]_\times] = [\boldsymbol{\omega}_1 \times \boldsymbol{\omega}_2]_\times [[ω1]×,[ω2]×]=[ω1×ω2]×
这意味着在 s o ( 3 ) \mathfrak{so}(3) so(3)中,李括号运算等价于三维向量空间中的叉积运算, s o ( 3 ) \mathfrak{so}(3) so(3)与上一小节中介绍的李代数 ( R 3 , × ) (\mathbb{R}^3, \times) (R3,×)的含义基本相同。
举例验证一下,假设有两个向量 ω 1 = ( 1 , 0 , 0 ) T \boldsymbol{\omega}_1 = (1, 0, 0)^T ω1=(1,0,0)T和 ω 2 = ( 0 , 1 , 0 ) T \boldsymbol{\omega}_2 = (0, 1, 0)^T ω2=(0,1,0)T,它们对应的反对称矩阵分别是:
[ ω 1 ] × = [ 0 0 0 0 0 − 1 0 1 0 ] , [ ω 2 ] × = [ 0 0 1 0 0 0 − 1 0 0 ] [\boldsymbol{\omega}_1]_\times = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{bmatrix}, \quad [\boldsymbol{\omega}_2]_\times = \begin{bmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ -1 & 0 & 0 \end{bmatrix} [ω1]×= 0000010−10 ,[ω2]×= 00−1000100
计算它们的李括号:
[ [ ω 1 ] × , [ ω 2 ] × ] = [ 0 0 0 0 0 − 1 0 1 0 ] [ 0 0 1 0 0 0 − 1 0 0 ] − [ 0 0 1 0 0 0 − 1 0 0 ] [ 0 0 0 0 0 − 1 0 1 0 ] [[\boldsymbol{\omega}_1]_\times, [\boldsymbol{\omega}_2]_\times] = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ -1 & 0 & 0 \end{bmatrix} - \begin{bmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ -1 & 0 & 0 \end{bmatrix} \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{bmatrix} [[ω1]×,[ω2]×]= 0000010−10 00−1000100 − 00−1000100 0000010−10
= [ 0 0 0 1 0 0 0 0 − 1 ] − [ 0 0 − 1 0 0 0 1 0 0 ] = [ 0 0 1 − 1 0 0 0 − 1 0 ] = \begin{bmatrix} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & -1 \end{bmatrix} - \begin{bmatrix} 0 & 0 & -1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \end{bmatrix} = \begin{bmatrix} 0 & 0 & 1 \\ -1 & 0 & 0 \\ 0 & -1 & 0 \end{bmatrix} = 01000000−1 − 001000−100 = 0−1000−1100
这正是 [ 0 , 0 , 1 ] T [0, 0, 1]^T [0,0,1]T向量对应的反对称矩阵,也就是 ω 1 × ω 2 = ( 0 , 0 , 1 ) T \boldsymbol{\omega}_1 \times \boldsymbol{\omega}_2 = (0, 0, 1)^T ω1×ω2=(0,0,1)T。
2.4 李代数 s e ( 3 ) \mathfrak{se}(3) se(3)
与引出特殊正交群 S O ( 3 ) SO(3) SO(3)的李代数 s o ( 3 ) \mathfrak{so}(3) so(3)的推导一样,也可以对特殊欧式群 S E ( 3 ) SE(3) SE(3)对时间 t t t微分来引出对应的李代数 s e ( 3 ) \mathfrak{se}(3) se(3)。假设一个刚体在三维空间随时间做欧式运动(即刚体运动,同时包括旋转和平移),那么欧式变换矩阵可以表示为:
T ( t ) = [ R ( t ) p ( t ) 0 T 1 ] ∈ S E ( 3 ) T(t) = \begin{bmatrix} R(t) & \boldsymbol{p}(t) \\ \mathbf{0}^T & 1 \end{bmatrix} \in SE(3) T(t)=[R(t)0Tp(t)1]∈SE(3)
其中:
- R ( t ) ∈ S O ( 3 ) R(t) \in SO(3) R(t)∈SO(3) 表示旋转;
- p ( t ) ∈ R 3 \boldsymbol{p}(t) \in \mathbb{R}^3 p(t)∈R3 表示平移;
- 整个矩阵是一个 4 × 4 4 \times 4 4×4的齐次变换矩阵。
对 T ( t ) T(t) T(t)的自变量时间 t t t进行微分,即:
d d t T ( t ) = d d t [ R ( t ) p ( t ) 0 T 1 ] = [ d d t R ( t ) d d t p ( t ) 0 T 0 ] \frac{d}{dt} T(t) = \frac{d}{dt} \begin{bmatrix} R(t) & \boldsymbol{p}(t) \\ \mathbf{0}^T & 1 \end{bmatrix}= \begin{bmatrix} \frac{d}{dt} R(t) & \frac{d}{dt} \boldsymbol{p}(t) \\ \mathbf{0}^T & 0 \end{bmatrix} dtdT(t)=dtd[R(t)0Tp(t)1]=[dtdR(t)0Tdtdp(t)0]
其中 d d t R ( t ) = [ ω ( t ) ] × R ( t ) \frac{d}{dt} R(t) = [\boldsymbol{\omega}(t)]_\times R(t) dtdR(t)=[ω(t)]×R(t),这一点我们在前面引出李代数 s o ( 3 ) \mathfrak{so}(3) so(3)的时候推导过。 p ( t ) \boldsymbol{p}(t) p(t)表示位移,那么 p ( t ) \boldsymbol{p}(t) p(t)对时间 t t t求导,即 d d t p ( t ) = v ( t ) \frac{d}{dt} \boldsymbol{p}(t) = \boldsymbol{v}(t) dtdp(t)=v(t)是瞬时线速度。
因此:
d d t T ( t ) = [ [ ω ( t ) ] × R ( t ) v ( t ) 0 T 0 ] (1) \frac{d}{dt} T(t) = \begin{bmatrix} [\boldsymbol{\omega}(t)]_\times R(t) & \boldsymbol{v}(t) \\ \mathbf{0}^T & 0 \end{bmatrix} \tag{1} dtdT(t)=[[ω(t)]×R(t)0Tv(t)0](1)
需要进一步说明的是, v ( t ) \boldsymbol{v}(t) v(t) 是空间坐标系下的线速度。我们知道速度是一种矢量,而欧式变换包含旋转和平移两种变换,那么空间坐标系下线速度 v ( t ) \boldsymbol{v}(t) v(t)可以分解成:
- 由于旋转引起的“附加速度”:即使没有自身的平移,只要它在旋转,它上面的点也会因为旋转而产生一个速度。
- 由于自身平移产生的速度:这是物体本身在自己坐标系下的移动速度。
数学表达如下:
v ( t ) = [ ω ( t ) ] × p ( t ) + v body ( t ) (2) \boldsymbol{v}(t) = [\boldsymbol{\omega}(t)]_\times \boldsymbol{p}(t) + \boldsymbol{v}_{\text{body}}(t) \tag{2} v(t)=[ω(t)]×p(t)+vbody(t)(2)
这个公式其实就是刚体运动学中的速度合成公式:
- v body \boldsymbol{v}_{\text{body}} vbody就是刚体自身平移产生的速度,即体坐标系下的线速度;
- ω ( t ) \boldsymbol{\omega}(t) ω(t)是刚体的角速度,通常也在体坐标系下表示;
- p ( t ) \boldsymbol{p}(t) p(t)表示相对于刚体原点的位置向量。
- [ ω ( t ) ] × p ( t ) [\boldsymbol{\omega}(t)]_\times \boldsymbol{p}(t) [ω(t)]×p(t)就是由于旋转引起的附加速度,其是一种典型的圆周运动的速度: ω ( t ) \boldsymbol{\omega}(t) ω(t)方向垂直于圆周面, p ( t ) \boldsymbol{p}(t) p(t)定义了到旋转中心的距离半径,两者叉乘,即得因刚体旋转而具有的切向速度。
将式(2)代入式(1),有:
d d t T ( t ) = [ [ ω ( t ) ] × R ( t ) [ ω ( t ) ] × p ( t ) + v body ( t ) 0 T 0 ] = [ [ ω ( t ) ] × v body ( t ) 0 T 0 ] [ R ( t ) p ( t ) 0 T 1 ] \begin{align*} \frac{d}{dt} T(t) &= \begin{bmatrix} [\boldsymbol{\omega}(t)]_\times R(t) & [\boldsymbol{\omega}(t)]_\times \boldsymbol{p}(t) + \boldsymbol{v}_{\text{body}}(t) \\ \mathbf{0}^T & 0 \end{bmatrix} \\ &= \begin{bmatrix} [\boldsymbol{\omega}(t)]_\times & \boldsymbol{v}_{\text{body}}(t) \\ \mathbf{0}^T & 0 \end{bmatrix} \begin{bmatrix} R(t) & \boldsymbol{p}(t) \\ \mathbf{0}^T & 1 \end{bmatrix} \\ \end{align*} dtdT(t)=[[ω(t)]×R(t)0T[ω(t)]×p(t)+vbody(t)0]=[[ω(t)]×0Tvbody(t)0][R(t)0Tp(t)1]
如果令:
ξ ( t ) = [ [ ω ( t ) ] × v body ( t ) 0 T 0 ] \xi(t) = \begin{bmatrix} [\boldsymbol{\omega}(t)]_\times & \boldsymbol{v}_{\text{body}}(t) \\ \mathbf{0}^T & 0 \end{bmatrix} ξ(t)=[[ω(t)]×0Tvbody(t)0]
那么有:
d d t T ( t ) = ξ ( t ) T ( t ) \frac{d}{dt} T(t) = \xi(t) T(t) dtdT(t)=ξ(t)T(t)
显然,在初始时刻欧式变换矩阵为单位矩阵,即 T ( 0 ) = I 4 T(0) = I_4 T(0)=I4,那么有微分方程:
d d t T ( t ) = ξ ( t ) T ( t ) , T ( 0 ) = I 4 \frac{d}{dt} T(t) = \xi(t) T(t), \quad T(0) = I_4 dtdT(t)=ξ(t)T(t),T(0)=I4
这就又回到了上一篇文章《详解SLAM中的李群和李代数(上)》中介绍的一阶线性微分方程,其解为:
T ( t ) = exp ( ξ ( t ) t ) T(t) = \exp(\xi(t) t) T(t)=exp(ξ(t)t)
这就是从李代数 s e ( 3 ) \mathfrak{se}(3) se(3)到李群 S E ( 3 ) SE(3) SE(3)的指数映射,矩阵 ξ ( t ) \xi(t) ξ(t)就是 S E ( 3 ) SE(3) SE(3)的李代数中集合的元素。
进一步的,去掉自变量 t t t,将 v body \boldsymbol{v}_{\text{body}} vbody重命名为 v \boldsymbol{v} v,李代数 s e ( 3 ) \mathfrak{se}(3) se(3) 是所有形如:
ξ = [ [ ω ] × v 0 T 0 ] ∈ R 4 × 4 \xi = \begin{bmatrix} [\boldsymbol{\omega}]_\times & \boldsymbol{v} \\ \mathbf{0}^T & 0 \end{bmatrix} \in \mathbb{R}^{4 \times 4} ξ=[[ω]×0Tv0]∈R4×4
的矩阵构成的集合,其中 ω , v ∈ R 3 \boldsymbol{\omega}, \boldsymbol{v} \in \mathbb{R}^3 ω,v∈R3。
将其简记为:
s e ( 3 ) = { [ [ ω ] × v 0 T 0 ] | ω , v ∈ R 3 } \mathfrak{se}(3) = \left\{ \begin{bmatrix} [\boldsymbol{\omega}]_\times & \boldsymbol{v} \\ \mathbf{0}^T & 0 \end{bmatrix} \,\middle|\, \boldsymbol{\omega}, \boldsymbol{v} \in \mathbb{R}^3 \right\} se(3)={[[ω]×0Tv0] ω,v∈R3}
如果, s e ( 3 ) \mathfrak{se}(3) se(3)也可以用一个六维向量来表示:
η = [ ω v ] ∈ R 6 \boldsymbol{\eta} = \begin{bmatrix} \boldsymbol{\omega} \\ \boldsymbol{v} \end{bmatrix} \in \mathbb{R}^6 η=[ωv]∈R6
并定义对应的映射:
η ^ = [ [ ω ] × v 0 T 0 ] \hat{\boldsymbol{\eta}} = \begin{bmatrix} [\boldsymbol{\omega}]_\times & \boldsymbol{v} \\ \mathbf{0}^T & 0 \end{bmatrix} η^=[[ω]×0Tv0]
所以 s e ( 3 ) \mathfrak{se}(3) se(3)也可以表示为:
s e ( 3 ) = { η ^ | η ∈ R 6 } \mathfrak{se}(3) = \left\{ \hat{\boldsymbol{\eta}} \,\middle|\, \boldsymbol{\eta} \in \mathbb{R}^6 \right\} se(3)={η^ η∈R6}
2.5 s e ( 3 ) \mathfrak{se}(3) se(3)的李括号
s e ( 3 ) \mathfrak{se}(3) se(3) 中的李括号仍然是矩阵换位子。对于任意两个 ξ 1 , ξ 2 ∈ s e ( 3 ) \xi_1, \xi_2 \in \mathfrak{se}(3) ξ1,ξ2∈se(3),有:
[ ξ 1 , ξ 2 ] = ξ 1 ξ 2 − ξ 2 ξ 1 [\xi_1, \xi_2] = \xi_1 \xi_2 - \xi_2 \xi_1 [ξ1,ξ2]=ξ1ξ2−ξ2ξ1
如果写成向量形式 η 1 = ( ω 1 , v 1 ) T \boldsymbol{\eta}_1 = (\boldsymbol{\omega}_1, \boldsymbol{v}_1)^T η1=(ω1,v1)T, η 2 = ( ω 2 , v 2 ) T \boldsymbol{\eta}_2 = (\boldsymbol{\omega}_2, \boldsymbol{v}_2)^T η2=(ω2,v2)T,则可以推出:
[ η 1 , η 2 ] = [ ω 1 × ω 2 ω 1 × v 2 − ω 2 × v 1 ] [\boldsymbol{\eta}_1, \boldsymbol{\eta}_2] = \begin{bmatrix} \boldsymbol{\omega}_1 \times \boldsymbol{\omega}_2 \\ \boldsymbol{\omega}_1 \times \boldsymbol{v}_2 - \boldsymbol{\omega}_2 \times \boldsymbol{v}_1 \end{bmatrix} [η1,η2]=[ω1×ω2ω1×v2−ω2×v1]
这是通过直接计算矩阵乘积和利用叉积与反对称矩阵的关系推导出来的,估计也不是很常用,因此略掉推导过程。
3 指数映射
3.1 预备知识
3.1.1 泰勒公式
设一个函数 f ( x ) f(x) f(x) 在点 x = a x = a x=a 处无穷可导,那么它可以展开为如下形式的泰勒级数:
f ( x ) = ∑ n = 0 ∞ f ( n ) ( a ) n ! ( x − a ) n f(x) = \sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!}(x - a)^n f(x)=n=0∑∞n!f(n)(a)(x−a)n
这个式子的意思是:用无穷多个多项式项来逼近原函数 f ( x ) f(x) f(x)。
如果取 a = 0 a = 0 a=0,则称为麦克劳林级数(Maclaurin series):
f ( x ) = ∑ n = 0 ∞ f ( n ) ( 0 ) n ! x n f(x) = \sum_{n=0}^\infty \frac{f^{(n)}(0)}{n!}x^n f(x)=n=0∑∞n!f(n)(0)xn
根据这个定义,有:
e x = ∑ n = 0 ∞ 1 n ! x n = 1 + x + x 2 2 ! + x 3 3 ! + ⋯ sin ( x ) = x − x 3 3 ! + x 5 5 ! − x 7 7 ! + ⋯ = ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) ! cos ( x ) = 1 − x 2 2 ! + x 4 4 ! − x 6 6 ! + ⋯ = ∑ n = 0 ∞ ( − 1 ) n x 2 n ( 2 n ) ! e^x = \sum_{n=0}^\infty \frac{1}{n!}x^n = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots \\ \sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots = \sum_{n=0}^\infty (-1)^n \frac{x^{2n+1}}{(2n+1)!}\\ \cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots = \sum_{n=0}^\infty (-1)^n \frac{x^{2n}}{(2n)!} ex=n=0∑∞n!1xn=1+x+2!x2+3!x3+⋯sin(x)=x−3!x3+5!x5−7!x7+⋯=n=0∑∞(−1)n(2n+1)!x2n+1cos(x)=1−2!x2+4!x4−6!x6+⋯=n=0∑∞(−1)n(2n)!x2n
3.1.2 反对称矩阵的幂次规律
给定一个单位三维向量 ω = ( ω 1 , ω 2 , ω 3 ) T \boldsymbol{\omega} = (\omega_1, \omega_2, \omega_3)^T ω=(ω1,ω2,ω3)T,其对应的反对称矩阵 [ ω ] × [\boldsymbol{\omega}]_\times [ω]× 为:
[ ω ] × = [ 0 − ω 3 ω 2 ω 3 0 − ω 1 − ω 2 ω 1 0 ] [\boldsymbol{\omega}]_\times = \begin{bmatrix} 0 & -\omega_3 & \omega_2 \\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0 \end{bmatrix} [ω]×= 0ω3−ω2−ω30ω1ω2−ω10
假设 A = [ ω ] × A = [\boldsymbol{\omega}]_\times A=[ω]×,我们首先计算 A 2 A^2 A2:
A 2 = [ ω ] × 2 = [ 0 − ω 3 ω 2 ω 3 0 − ω 1 − ω 2 ω 1 0 ] [ 0 − ω 3 ω 2 ω 3 0 − ω 1 − ω 2 ω 1 0 ] A^2 = [\boldsymbol{\omega}]_\times^2 = \begin{bmatrix} 0 & -\omega_3 & \omega_2 \\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0 \end{bmatrix} \begin{bmatrix} 0 & -\omega_3 & \omega_2 \\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0 \end{bmatrix} A2=[ω]×2= 0ω3−ω2−ω30ω1ω2−ω10 0ω3−ω2−ω30ω1ω2−ω10
进行矩阵乘法运算后得到:
A 2 = [ − ω 2 2 − ω 3 2 ω 1 ω 2 ω 1 ω 3 ω 1 ω 2 − ω 1 2 − ω 3 2 ω 2 ω 3 ω 1 ω 3 ω 2 ω 3 − ω 1 2 − ω 2 2 ] A^2 = \begin{bmatrix} -\omega_2^2 - \omega_3^2 & \omega_1 \omega_2 & \omega_1 \omega_3 \\ \omega_1 \omega_2 & -\omega_1^2 - \omega_3^2 & \omega_2 \omega_3 \\ \omega_1 \omega_3 & \omega_2 \omega_3 & -\omega_1^2 - \omega_2^2 \end{bmatrix} A2= −ω22−ω32ω1ω2ω1ω3ω1ω2−ω12−ω32ω2ω3ω1ω3ω2ω3−ω12−ω22
因为这里 ω \boldsymbol{\omega} ω 是单位向量(即 ω 1 2 + ω 2 2 + ω 3 2 = 1 \omega_1^2 + \omega_2^2 + \omega_3^2 = 1 ω12+ω22+ω32=1),则:
A 2 = [ − ( 1 − ω 1 2 ) ω 1 ω 2 ω 1 ω 3 ω 1 ω 2 − ( 1 − ω 2 2 ) ω 2 ω 3 ω 1 ω 3 ω 2 ω 3 − ( 1 − ω 3 2 ) ] A^2 = \begin{bmatrix} -(1 - \omega_1^2) & \omega_1 \omega_2 & \omega_1 \omega_3 \\ \omega_1 \omega_2 & -(1 - \omega_2^2) & \omega_2 \omega_3 \\ \omega_1 \omega_3 & \omega_2 \omega_3 & -(1 - \omega_3^2) \end{bmatrix} A2= −(1−ω12)ω1ω2ω1ω3ω1ω2−(1−ω22)ω2ω3ω1ω3ω2ω3−(1−ω32)
进一步简化为:
A 2 = [ − ω 1 2 ω 1 ω 2 ω 1 ω 3 ω 1 ω 2 − ω 2 2 ω 2 ω 3 ω 1 ω 3 ω 2 ω 3 − ω 3 2 ] = ω ω T − I A^2 = \begin{bmatrix} -\omega_1^2 & \omega_1 \omega_2 & \omega_1 \omega_3 \\ \omega_1 \omega_2 & -\omega_2^2 & \omega_2 \omega_3 \\ \omega_1 \omega_3 & \omega_2 \omega_3 & -\omega_3^2 \end{bmatrix} = \boldsymbol{\omega} \boldsymbol{\omega}^T - \mathbf{I} A2= −ω12ω1ω2ω1ω3ω1ω2−ω22ω2ω3ω1ω3ω2ω3−ω32 =ωωT−I
这里 I \mathbf{I} I 是单位矩阵, ω ω T \boldsymbol{\omega} \boldsymbol{\omega}^T ωωT 是外积矩阵。
接下来计算 A 3 A^3 A3:
A 3 = A ⋅ A 2 = [ ω ] × ⋅ ( ω ω T − I ) A^3 = A \cdot A^2 = [\boldsymbol{\omega}]_\times \cdot (\boldsymbol{\omega} \boldsymbol{\omega}^T - \mathbf{I}) A3=A⋅A2=[ω]×⋅(ωωT−I)
注意到 [ ω ] × ω = 0 [\boldsymbol{\omega}]_\times \boldsymbol{\omega} = \mathbf{0} [ω]×ω=0 (因为反对称矩阵作用于自身方向的向量结果为零向量),因此:
A 3 = − [ ω ] × + [ ω ] × ( ω ω T ) = − [ ω ] × = − A A^3 = -[\boldsymbol{\omega}]_\times + [\boldsymbol{\omega}]_\times (\boldsymbol{\omega} \boldsymbol{\omega}^T) = -[\boldsymbol{\omega}]_\times = -A A3=−[ω]×+[ω]×(ωωT)=−[ω]×=−A
所以:
A 3 = − A A^3 = -A A3=−A
再来看计算 A 4 A^4 A4:
A 4 = A ⋅ A 3 = A ⋅ ( − A ) = − A 2 A^4 = A \cdot A^3 = A \cdot (-A) = -A^2 A4=A⋅A3=A⋅(−A)=−A2
根据前面的结果 A 2 = ω ω T − I A^2 = \boldsymbol{\omega} \boldsymbol{\omega}^T - \mathbf{I} A2=ωωT−I,于是:
A 4 = − ( ω ω T − I ) = − A 2 A^4 = -(\boldsymbol{\omega} \boldsymbol{\omega}^T - \mathbf{I}) = -A^2 A4=−(ωωT−I)=−A2
因此:
A 4 = − A 2 A^4 = -A^2 A4=−A2
最后计算 A 5 A^5 A5:
A 5 = A ⋅ A 4 = A ⋅ ( − A 2 ) = − A 3 = − ( − A ) = A A^5 = A \cdot A^4 = A \cdot (-A^2) = -A^3 = -(-A) = A A5=A⋅A4=A⋅(−A2)=−A3=−(−A)=A
所以:
A 5 = A A^5 = A A5=A
通过上述推导,我们可以总结出反对称矩阵 A = [ ω ] × A = [\boldsymbol{\omega}]_\times A=[ω]× 的一些重要幂次规律:
- A = [ ω ] × A = [\boldsymbol{\omega}]_\times A=[ω]×
- A 2 = ω ω T − I A^2 = \boldsymbol{\omega} \boldsymbol{\omega}^T-\mathbf{I} A2=ωωT−I
- A 3 = − A A^3 = -A A3=−A
- A 4 = − A 2 A^4 = -A^2 A4=−A2
- A 5 = A A^5 = A A5=A
- A 6 = A 2 A^6 = A^2 A6=A2
- A 7 = − A A^7 = -A A7=−A
- A 8 = − A 2 A^8 = -A^2 A8=−A2
这些规律表明,对于反对称矩阵 A = [ ω ] × A = [\boldsymbol{\omega}]_\times A=[ω]×,其高次幂具有周期性,并且可以归约为 A A A、 A 2 A^2 A2 和 − A -A −A 的线性组合。
3.1.3 Chasles定理
从 S O ( 3 ) SO(3) SO(3)李代数的推导可以知道,任何旋转变换可以等效为绕某个固定轴的旋转来表示,那么欧式变换(刚体变换)是不是也有类似的性质呢?确实如此,刚体运动学的Chasles定理指出:
任何一个刚体的位移都可以视为绕某条直线(称为螺旋轴或瞬时转动轴)的旋转加上沿这条直线的平移。
换句话说,任何刚体的位移可以分解为绕一个特定方向的旋转加上沿着这个方向的平移。这种组合运动被称为螺旋运动,这条特定方向确定的直线就是螺旋轴。在刚体运动过程中,这条直线是保持不变的。
根据前面 S E ( 3 ) SE(3) SE(3)李代数推导可知,欧式变换可以表示为:
T = exp ( ξ ) T = \exp(\xi) T=exp(ξ)
如同旋转变换的旋转向量可以分解成单位轴向量和旋转角度一样,螺旋运动也可以由以下两个量来确定:
- 单位螺旋轴 s ^ \hat{s} s^:描述运动的方向(包括旋转轴和平移方向)。
- 标量 θ \theta θ:描述沿这个螺旋轴运动了多远。
即:
ξ = s ^ θ \xi = \hat{s} \theta ξ=s^θ
于是整个运动就可以写成:
T = exp ( s ^ θ ) T = \exp(\hat{s} \theta) T=exp(s^θ)
又因为:
ξ = [ [ ω ] × v 0 T 0 ] ∈ R 4 × 4 \xi = \begin{bmatrix} [\boldsymbol{\omega}]_\times & \boldsymbol{v} \\ \mathbf{0}^T & 0 \end{bmatrix} \in \mathbb{R}^{4 \times 4} ξ=[[ω]×0Tv0]∈R4×4
对这个矩阵提取 θ \theta θ,很显然:
- [ ω ] × = θ ⋅ [ ω unit ] × [\boldsymbol{\omega}]_\times = \theta \cdot [\boldsymbol{\omega}_{\text{unit}}]_\times [ω]×=θ⋅[ωunit]×
- 0 T = θ ⋅ 0 T \mathbf{0}^T = \theta \cdot \mathbf{0}^T 0T=θ⋅0T
- 0 = θ ⋅ 0 0 = \theta \cdot 0 0=θ⋅0
那么必然存在单位螺旋轴 s ^ \hat{s} s^ 的矩阵:
s ^ = [ [ ω unit ] × v unit 0 T 0 ] \hat{s} = \begin{bmatrix} [\boldsymbol{\omega}_{\text{unit}}]_\times & \boldsymbol{v}_{\text{unit}} \\ \mathbf{0}^T & 0 \end{bmatrix} s^=[[ωunit]×0Tvunit0]
能满足 v = θ ⋅ v unit \boldsymbol{v} = \theta \cdot \boldsymbol{v}_{\text{unit}} v=θ⋅vunit。这里的 ω unit \boldsymbol{\omega}_{\text{unit}} ωunit 是单位旋转轴, v unit \boldsymbol{v}_{\text{unit}} vunit 是单位平移速度向量。
可能在这里有的读者会觉得有点难以理解,平移和旋转是两个独立的运动,为什么会共享同一个参数 θ \theta θ?其实这里把螺旋运动理解成向一个木板拧螺丝就行了,拧螺丝拧的角度越大,打进木板的距离就越远。这里的 θ \theta θ是一个统一的“运动参数”,它决定了旋转了多少、平移了多少,就像是“沿某个固定运动方向走多远”的度量。
数学上的表达总结如下:
ξ = θ ⋅ s ^ = θ ⋅ [ [ ω unit ] × v unit 0 T 0 ] = [ [ ω ] × v 0 T 0 ] {\xi} = \theta \cdot \hat{s} = \theta \cdot \begin{bmatrix} [\boldsymbol{\omega}_{\text{unit}}]_\times & \boldsymbol{v}_{\text{unit}} \\ \mathbf{0}^T & 0 \end{bmatrix}= \begin{bmatrix} [\boldsymbol{\omega}]_\times & \boldsymbol{v} \\ \mathbf{0}^T & 0 \end{bmatrix} ξ=θ⋅s^=θ⋅[[ωunit]×0Tvunit0]=[[ω]×0Tv0]
3.2 S O ( 3 ) SO(3) SO(3)上的指数映射
根据前面的推导,已知旋转矩阵 R ∈ S O ( 3 ) R \in SO(3) R∈SO(3) 可以通过李代数 s o ( 3 ) \mathfrak{so}(3) so(3) 的指数映射来表示:
R = exp ( [ ω ] × ) R = \exp([\boldsymbol{\omega}]_\times) R=exp([ω]×)
这里的 ω \boldsymbol{\omega} ω就是旋转向量,我们知道向量都等于自身的单位向量与模长的乘积,那么可以令 a a a为 ω \boldsymbol{\omega} ω的单位向量, θ \theta θ 为 ω \boldsymbol{\omega} ω的模长。也即是:
ω = θ a \boldsymbol{\omega} = {\theta}a ω=θa
取反对称矩阵,有:
[ ω ] × = [ θ a ] × = θ [ a ] × [\boldsymbol{\omega}]_\times = [{\theta}a]_\times = {\theta}[a]_\times [ω]×=[θa]×=θ[a]×
令 A = [ a ] × A = [a]_\times A=[a]×,根据预备知识介绍的泰勒公式,将标量指数函数推广到矩阵指数函数上,有:
R = exp ( θ A ) = ∑ n = 0 ∞ ( θ A ) n n ! R = \exp({\theta}A) = \sum_{n=0}^\infty \frac{({\theta}A)^n}{n!} R=exp(θA)=n=0∑∞n!(θA)n
将 exp ( θ A ) \exp(\theta A) exp(θA) 展开为泰勒级数:
exp ( θ A ) = I + θ A + θ 2 2 ! A 2 + θ 3 3 ! A 3 + θ 4 4 ! A 4 + ⋯ \exp(\theta A) = I + \theta A + \frac{\theta^2}{2!} A^2 + \frac{\theta^3}{3!} A^3 + \frac{\theta^4}{4!} A^4 + \cdots exp(θA)=I+θA+2!θ2A2+3!θ3A3+4!θ4A4+⋯
利用预备知识中提到的反对称矩阵的(如 A 3 = − A A^3 = -A A3=−A, A 4 = − A 2 A^4 = -A^2 A4=−A2 等),我们可以把所有项都写成 I , A , A 2 I, A, A^2 I,A,A2 的线性组合:
exp ( θ A ) = I + θ A + θ 2 2 ! A 2 − θ 3 3 ! A − θ 4 4 ! A 2 + θ 5 5 ! A + ⋯ = I + ( θ − θ 3 3 ! + θ 5 5 ! − ⋯ ) A + ( θ 2 2 ! − θ 4 4 ! + ⋯ ) A 2 \begin{aligned} \exp(\theta A) &= I + \theta A + \frac{\theta^2}{2!} A^2 -\frac{\theta^3}{3!} A -\frac{\theta^4}{4!} A^2 +\frac{\theta^5}{5!} A +\cdots \\ &= I + \left(\theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \cdots\right) A \\ &\quad + \left(\frac{\theta^2}{2!} - \frac{\theta^4}{4!} + \cdots\right) A^2 \end{aligned} exp(θA)=I+θA+2!θ2A2−3!θ3A−4!θ4A2+5!θ5A+⋯=I+(θ−3!θ3+5!θ5−⋯)A+(2!θ2−4!θ4+⋯)A2
再利用预备知识中的正弦和余弦的泰勒公式展开:
- sin θ = θ − θ 3 3 ! + θ 5 5 ! − ⋯ \sin\theta = \theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \cdots sinθ=θ−3!θ3+5!θ5−⋯
- 1 − cos θ = θ 2 2 ! − θ 4 4 ! + ⋯ 1 - \cos\theta = \frac{\theta^2}{2!} - \frac{\theta^4}{4!} + \cdots 1−cosθ=2!θ2−4!θ4+⋯
所以:
exp ( θ A ) = I + sin θ ⋅ A + ( 1 − cos θ ) ⋅ A 2 \exp(\theta A) = I + \sin\theta \cdot A + (1 - \cos\theta) \cdot A^2 exp(θA)=I+sinθ⋅A+(1−cosθ)⋅A2
也可以表达为:
exp ( θ [ a ] × ) = cos θ I + ( 1 − cos θ ) a a T + sin θ [ a ] × \exp(\theta [a]_\times) = \cos\theta I + (1 - \cos\theta) a{a}^T +\sin\theta [a]_\times exp(θ[a]×)=cosθI+(1−cosθ)aaT+sinθ[a]×
其中, a a a为 s o ( 3 ) \mathfrak{so}(3) so(3)集合中元素 ω \boldsymbol{\omega} ω的单位向量, A A A为 a a a的反对称矩阵, θ \theta θ 为 ω \boldsymbol{\omega} ω的模长。其实这里的 ω \boldsymbol{\omega} ω就是旋转矩阵的旋转向量,这个公式也就是著名的罗德里格公式。
通过以上推导表明, s o ( 3 ) \mathfrak{so}(3) so(3)其实就是旋转向量组成的向量空间,指数映射就是罗德里格公式。通过罗德里格公式,任意一个向量都可以对应到 S O ( 3 ) SO(3) SO(3)中的旋转矩阵。反之,将 S O ( 3 ) SO(3) SO(3)对应到 s o ( 3 ) \mathfrak{so}(3) so(3)就是对数映射,当然这里就是不用列出对数表达式,在《视觉SLAM十四讲》的第3讲中介绍了更简便的计算方法:
θ = arccos ( tr ( R ) − 1 2 ) , R a = a \theta = \arccos\left( \frac{\operatorname{tr}(R) - 1}{2} \right),Ra = a θ=arccos(2tr(R)−1),Ra=a
在书上没有给出 R a = a Ra = a Ra=a的具体解的过程,因为可能有多个解的情况,表述起来比较麻烦,大概的求解过程是:
| 步骤 | 内容 |
|---|---|
| 1. | 计算旋转角度: θ = arccos ( tr ( R ) − 1 2 ) \theta = \arccos\left( \frac{\operatorname{tr}(R) - 1}{2} \right) θ=arccos(2tr(R)−1) |
| 2. | 若 θ = 0 \theta = 0 θ=0:返回 ω = 0 \boldsymbol{\omega} = \mathbf{0} ω=0 或任意方向 |
| 3. | 若 θ = π \theta = \pi θ=π:构造 ω ω T = 1 2 ( R + I ) \boldsymbol{\omega} \boldsymbol{\omega}^T = \frac{1}{2}(R + I) ωωT=21(R+I),取最大特征值对应的单位特征向量 |
| 4. | 否则:计算反对称部分 S = 1 2 ( R − R T ) S = \frac{1}{2}(R - R^T) S=21(R−RT),提取 ω = 1 2 sin θ [ S 32 S 13 S 21 ] \boldsymbol{\omega} = \frac{1}{2\sin\theta} \begin{bmatrix} S_{32} \\ S_{13} \\ S_{21} \end{bmatrix} ω=2sinθ1 S32S13S21 ,然后归一化 |
其实从求解对数映射的解就可以看出,指数映射是一个满射,而不是单射。也就是任意 S O ( 3 ) SO(3) SO(3)集合中的元素,都能在 s o ( 3 ) \mathfrak{so}(3) so(3)中找到一个元素与之对应;但是可能存在多个 s o ( 3 ) \mathfrak{so}(3) so(3)中的元素对应于一个 S O ( 3 ) SO(3) SO(3)集合中的元素。其实这个不难理解,旋转是有周期性的,旋转360度和不转是一样的,只有范围限定在 ( − π , + π ] (-\pi, +\pi] (−π,+π]之间,两者才可以一一对应。
3.3 S E ( 3 ) SE(3) SE(3)上的指数映射
根据前面的推导,特殊欧式群 S E ( 3 ) SE(3) SE(3)的李代数 s e ( 3 ) \mathfrak{se}(3) se(3),可以用一个4维矩阵表示,包含旋转和平移信息:
ξ = [ [ ω ] × v 0 T 0 ] ∈ R 4 × 4 \xi = \begin{bmatrix} [\boldsymbol{\omega}]_\times & \boldsymbol{v} \\ \mathbf{0}^T & 0 \end{bmatrix} \in \mathbb{R}^{4 \times 4} ξ=[[ω]×0Tv0]∈R4×4
其中 ω \boldsymbol{\omega} ω 就是特殊正交群 S O ( 3 ) SO(3) SO(3)的李代数的向量表示, v \boldsymbol{v} v 表示平移速度。
根据准备知识中介绍的Chasles定理,有:
T = exp ( ξ ) = exp ( s ^ θ ) T = \exp(\xi) = \exp(\hat{s} \theta) T=exp(ξ)=exp(s^θ)
其中 s ^ \hat{s} s^是单位螺旋轴矩阵:
s ^ = [ [ ω unit ] × v unit 0 T 0 ] \hat{s} = \begin{bmatrix} [\boldsymbol{\omega}_{\text{unit}}]_\times & \boldsymbol{v}_{\text{unit}} \\ \mathbf{0}^T & 0 \end{bmatrix} s^=[[ωunit]×0Tvunit0]
θ \theta θ则描述沿这个螺旋轴运动了多远。使用泰勒公式展开指数函数,有:
exp ( ξ ) = ∑ n = 0 ∞ ( s ^ θ ) n n ! = I + s ^ θ + ( s ^ θ ) 2 2 ! + ( s ^ θ ) 3 3 ! + ⋯ \exp({\xi}) = \sum_{n=0}^\infty \frac{(\hat{s}\theta)^n}{n!} = I + \hat{s} \theta + \frac{(\hat{s} \theta)^2}{2!} + \frac{(\hat{s} \theta)^3}{3!} + \cdots exp(ξ)=n=0∑∞n!(s^θ)n=I+s^θ+2!(s^θ)2+3!(s^θ)3+⋯
因此关键在于计算每一项 ( s ^ θ ) n (\hat{s}\theta)^n (s^θ)n。对于第0项:
I = [ I 0 0 T 1 ] I = \begin{bmatrix} I & \mathbf{0} \\ \mathbf{0}^T & 1 \end{bmatrix} I=[I0T01]
对于第1项,前面求 S O ( 3 ) SO(3) SO(3)的时候已经定义 A = [ ω unit ] × A = [\boldsymbol{\omega}_{\text{unit}}]_\times A=[ωunit]×,则:
s ^ θ = [ θ A θ v unit 0 T 0 ] = [ θ A v 0 T 0 ] \hat{s}\theta = \begin{bmatrix} \theta A & \theta \boldsymbol{v}_{\text{unit}} \\ \mathbf{0}^T & 0 \end{bmatrix} = \begin{bmatrix} \theta A & \boldsymbol{v} \\ \mathbf{0}^T & 0 \end{bmatrix} s^θ=[θA0Tθvunit0]=[θA0Tv0]
对于第2项:
( s ^ θ ) 2 2 ! = 1 2 ! [ ( θ A ) 2 θ A v 0 T 0 ] = [ ( θ A ) 2 2 ! ( θ A ) v 2 ! 0 T 0 ] \frac{(\hat{s} \theta)^2}{2!} = \frac{1}{2!} \begin{bmatrix} (\theta A)^2 & \theta A \boldsymbol{v} \\ \mathbf{0}^T & 0 \end{bmatrix}= \begin{bmatrix} \frac{(\theta A)^2}{2!} & \frac{(\theta A) \boldsymbol{v}}{2!} \\ \mathbf{0}^T & 0 \end{bmatrix} 2!(s^θ)2=2!1[(θA)20TθAv0]=[2!(θA)20T2!(θA)v0]
对于第3项:
( s ^ θ ) 3 3 ! = 1 3 ! [ ( θ A ) 3 ( θ A ) 2 v 0 T 0 ] = [ ( θ A ) 3 3 ! ( θ A ) 2 v 3 ! 0 T 0 ] \frac{(\hat{s} \theta)^3}{3!} = \frac{1}{3!} \begin{bmatrix} (\theta A)^3 & (\theta A)^2 \boldsymbol{v} \\ \mathbf{0}^T & 0 \end{bmatrix}= \begin{bmatrix} \frac{(\theta A)^3}{3!} & \frac{(\theta A)^2 \boldsymbol{v}}{3!} \\ \mathbf{0}^T & 0 \end{bmatrix} 3!(s^θ)3=3!1[(θA)30T(θA)2v0]=[3!(θA)30T3!(θA)2v0]
以此类推,把所有项加起来,分块相加,有:
exp ( ξ ) = I + s ^ θ + ( s ^ θ ) 2 2 ! + ( s ^ θ ) 3 3 ! + ⋯ = [ I 0 0 T 1 ] + [ θ A v 0 T 0 ] + [ ( θ A ) 2 2 ! ( θ A ) v 2 ! 0 T 0 ] + [ ( θ A ) 3 3 ! ( θ A ) 2 v 3 ! 0 T 0 ] + ⋯ = [ ∑ n = 0 ∞ ( θ A ) n n ! ∑ n = 1 ∞ ( θ A ) n − 1 v n ! 0 T 1 ] \begin{align*} \exp({\xi}) &= I + \hat{s} \theta + \frac{(\hat{s} \theta)^2}{2!} + \frac{(\hat{s} \theta)^3}{3!} + \cdots \\ &= \begin{bmatrix} I & \mathbf{0} \\ \mathbf{0}^T & 1 \end{bmatrix} + \begin{bmatrix} \theta A & \boldsymbol{v} \\ \mathbf{0}^T & 0 \end{bmatrix} + \begin{bmatrix} \frac{(\theta A)^2}{2!} & \frac{(\theta A) \boldsymbol{v}}{2!} \\ \mathbf{0}^T & 0 \end{bmatrix}+ \begin{bmatrix} \frac{(\theta A)^3}{3!} & \frac{(\theta A)^2 \boldsymbol{v}}{3!} \\ \mathbf{0}^T & 0 \end{bmatrix} + \cdots\\ &=\begin{bmatrix} \sum_{n=0}^\infty \frac{({\theta}A)^n}{n!} & \sum_{n=1}^\infty \frac{(\theta A)^{n-1} \boldsymbol{v}}{n!} \\ \mathbf{0}^T & 1 \\ \end{bmatrix} \end{align*} exp(ξ)=I+s^θ+2!(s^θ)2+3!(s^θ)3+⋯=[I0T01]+[θA0Tv0]+[2!(θA)20T2!(θA)v0]+[3!(θA)30T3!(θA)2v0]+⋯=[∑n=0∞n!(θA)n0T∑n=1∞n!(θA)n−1v1]
对于这个结果的左上角元素,其实就是 S O ( 3 ) SO(3) SO(3)的指数映射:
exp ( θ A ) = ∑ n = 0 ∞ ( θ A ) n n ! \exp(\theta A) = \sum_{n=0}^\infty \frac{({\theta}A)^n}{n!} exp(θA)=n=0∑∞n!(θA)n
而对于右上角元素,可以将索引平移一下,令 k = n − 1 k = n - 1 k=n−1,则:
∑ k = 0 ∞ ( θ A ) k v ( k + 1 ) ! \sum_{k=0}^\infty \frac{(\theta A)^k \boldsymbol{v}}{(k+1)!} k=0∑∞(k+1)!(θA)kv
因此, S E ( 3 ) SE(3) SE(3)指数映射可以写成:
exp ( ξ ) = [ exp ( θ A ) ∑ n = 0 ∞ ( θ A ) n v ( n + 1 ) ! 0 T 1 ] \exp({\xi}) = \begin{bmatrix} \exp(\theta A) & \sum_{n=0}^\infty \frac{(\theta A)^n \boldsymbol{v}}{(n+1)!} \\ \mathbf{0}^T & 1 \end{bmatrix} exp(ξ)=[exp(θA)0T∑n=0∞(n+1)!(θA)nv1]
但是为了进一步方便表达右上角元素的表达式,引入左不变雅可比矩阵 J J J:
J = ∑ n = 0 ∞ ( θ A ) n ( n + 1 ) ! J = \sum_{n=0}^\infty \frac{(\theta A)^n}{(n+1)!} J=n=0∑∞(n+1)!(θA)n
接下来利用预备知识中介绍的反对称矩阵的周期性规律计算 J J J:
J = I + θ 2 ! A + θ 2 3 ! A 2 + θ 3 4 ! A 3 + ⋯ = I + 1 θ ( θ 2 2 ! − θ 4 4 ! + ⋯ ) A + 1 θ ( θ 3 3 ! − θ 5 5 ! + ⋯ ) A 2 \begin{align*} J &= I + \frac{\theta}{2!}{A} + \frac{{\theta}^{2}}{3!}{A^2} + \frac{{\theta}^{3}}{4!}{A^3} + \cdots \\ &= I + \frac{1}{\theta}(\frac{\theta^{2}}{2!} - \frac{{\theta}^{4}}{4!} + \cdots) {A} + \frac{1}{\theta}(\frac{{\theta}^{3}}{3!}-\frac{{\theta}^{5}}{5!} + \cdots) {A^2} \end{align*} J=I+2!θA+3!θ2A2+4!θ3A3+⋯=I+θ1(2!θ2−4!θ4+⋯)A+θ1(3!θ3−5!θ5+⋯)A2
利用预备知识中的正弦和余弦的泰勒公式展开:
- θ − sin θ = θ 3 3 ! + θ 5 5 ! − ⋯ \theta - \sin\theta = \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \cdots θ−sinθ=3!θ3+5!θ5−⋯
- 1 − cos θ = θ 2 2 ! − θ 4 4 ! + ⋯ 1 - \cos\theta = \frac{\theta^2}{2!} - \frac{\theta^4}{4!} + \cdots 1−cosθ=2!θ2−4!θ4+⋯
可以得到:
J = I + 1 − cos θ θ A + θ − sin θ θ A 2 J = I + \frac{1 - \cos\theta}{\theta} A + \frac{\theta - \sin\theta}{\theta} A^2 J=I+θ1−cosθA+θθ−sinθA2
由于 A = [ a ] × A = [a]_\times A=[a]×,因此 J J J也可以表达为:
J = I + 1 − cos θ θ [ a ] × + θ − sin θ θ ( a a T − I ) = sin θ θ I + ( 1 − sin θ θ ) a a T + 1 − cos θ θ [ a ] × \begin{align*} J &= I + \frac{1 - \cos\theta}{\theta} [a]_\times + \frac{\theta - \sin\theta}{\theta} ({a}{a^T}-\mathbf{I})\\ &= \frac{\sin\theta}{\theta}I + (1 - \frac{\sin\theta}{\theta}){a}{a^T} + \frac{1 - \cos\theta}{\theta} [a]_\times\\ \end{align*} J=I+θ1−cosθ[a]×+θθ−sinθ(aaT−I)=θsinθI+(1−θsinθ)aaT+θ1−cosθ[a]×
S E ( 3 ) SE(3) SE(3)的指数映射最终结果如下:
exp ( ξ ) = [ exp ( [ ω ] × ) J v 0 T 1 ] \exp({\xi}) = \begin{bmatrix} \exp([\boldsymbol{\omega}]_\times) & J\boldsymbol{v} \\ \mathbf{0}^T & 1 \end{bmatrix} exp(ξ)=[exp([ω]×)0TJv1]
其中:
- 旋转部分 R = exp ( [ ω ] × ) R = \exp([\boldsymbol{\omega}]_\times) R=exp([ω]×)即 S O ( 3 ) SO(3) SO(3)的指数映射。
- 平移部分 t = J v \boldsymbol{t} = J\boldsymbol{v} t=Jv, 其中J是左不变雅可比矩阵:
J = I + 1 − cos θ θ A + θ − sin θ θ J = I + \frac{1 - \cos\theta}{\theta} A + \frac{\theta - \sin\theta}{\theta} J=I+θ1−cosθA+θθ−sinθ
或
J = sin θ θ I + ( 1 − sin θ θ ) a a T + 1 − cos θ θ [ a ] × J=\frac{\sin\theta}{\theta}I + (1 - \frac{\sin\theta}{\theta}){a}{a^T} + \frac{1 - \cos\theta}{\theta} [a]_\times J=θsinθI+(1−θsinθ)aaT+θ1−cosθ[a]×
与 S O ( 3 ) SO(3) SO(3)类似,也可以推导出 S E ( 3 ) SE(3) SE(3)到 s e ( 3 ) \mathfrak{se}(3) se(3)的对数映射。旋转部分可以按照之前介绍的 S O ( 3 ) SO(3) SO(3)到 s o ( 3 ) \mathfrak{so}(3) so(3)的对数映射求出;平移部分由于 J J J已知(通过左不变雅可比矩阵求得),可以解 t = J v \boldsymbol{t} = J\boldsymbol{v} t=Jv这个线性方程组来解得。具体数学表达式如下:
θ = arccos ( tr ( R ) − 1 2 ) , R a = a , t = J v \theta = \arccos\left( \frac{\operatorname{tr}(R) - 1}{2} \right),Ra = a,\boldsymbol{t} = J\boldsymbol{v} θ=arccos(2tr(R)−1),Ra=a,t=Jv
4 总结
作为本篇的结束,整理了一张特殊正交群的内容的表格,如下所示:
| 内容 | 特殊正交群 |
|---|---|
| 李群 | S O ( 3 ) = { R ∈ R 3 × 3 ∣ R T R = I , det ( R ) = 1 } SO(3) = \{ R \in \mathbb{R}^{3\times3} \mid R^T R = I, \det(R) = 1\} SO(3)={R∈R3×3∣RTR=I,det(R)=1} |
| 李代数 | s o ( 3 ) = { [ ω ] × ∈ R 3 × 3 ∣ ω ∈ R 3 } \mathfrak{so}(3) = \left\{ [\boldsymbol{\omega}]_\times \in \mathbb{R}^{3 \times 3} \mid {\omega} \in \mathbb{R}^3 \right\} so(3)={[ω]×∈R3×3∣ω∈R3} |
| 向量表示 | ω ∈ R 3 {\omega} \in \mathbb{R}^3 ω∈R3 |
| 李括号 | [ [ ω 1 ] × , [ ω 2 ] × ] = [ ω 1 ] × [ ω 2 ] × − [ ω 2 ] × [ ω 1 ] × [[\boldsymbol{\omega}_1]_\times, [\boldsymbol{\omega}_2]_\times] = [\boldsymbol{\omega}_1]_\times [\boldsymbol{\omega}_2]_\times - [\boldsymbol{\omega}_2]_\times [\boldsymbol{\omega}_1]_\times [[ω1]×,[ω2]×]=[ω1]×[ω2]×−[ω2]×[ω1]× 或者 叉乘 × \times × |
| 指数映射 | exp ( θ [ a ] × ) = cos θ I + ( 1 − cos θ ) a a T + sin θ [ a ] × \exp(\theta [a]_\times) = \cos\theta I + (1 - \cos\theta) a{a}^T +\sin\theta [a]_\times exp(θ[a]×)=cosθI+(1−cosθ)aaT+sinθ[a]× |
| 对数映射 | θ = arccos ( tr ( R ) − 1 2 ) , R a = a \theta = \arccos\left( \frac{\operatorname{tr}(R) - 1}{2} \right),Ra = a θ=arccos(2tr(R)−1),Ra=a |
特殊欧式群的内容则如下表所示:
| 内容 | 特殊欧式群 |
|---|---|
| 李群 | S E ( 3 ) = { T = [ R t 0 1 ] ∈ R 4 × 4 ∣ R ∈ S O ( 3 ) , t ∈ R 3 } SE(3)=\bigg\{ T = \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix} \in \mathbb{R}^{4\times4} \mid R \in SO(3) ,t \in \mathbb{R}^3 \bigg\} SE(3)={T=[R0t1]∈R4×4∣R∈SO(3),t∈R3} |
| 李代数 | s e ( 3 ) = { ξ = [ [ ω ] × v 0 T 0 ] ∈ R 4 × 4 ∣ ω , v ∈ R 3 } \mathfrak{se}(3) = \left\{\xi = \begin{bmatrix}[\boldsymbol{\omega}]_\times & \boldsymbol{v} \\ \mathbf{0}^T & 0 \\ \end{bmatrix} \in \mathbb{R}^{4 \times 4} \mid \boldsymbol{\omega}, \boldsymbol{v} \in \mathbb{R}^3 \right\} se(3)={ξ=[[ω]×0Tv0]∈R4×4∣ω,v∈R3} |
| 向量表示 | η = [ ω v ] ∈ R 6 \boldsymbol{\eta} = \begin{bmatrix} \boldsymbol{\omega} \\ \boldsymbol{v} \end{bmatrix} \in \mathbb{R}^6 η=[ωv]∈R6 |
| 李括号 | [ ξ 1 , ξ 2 ] = ξ 1 ξ 2 − ξ 2 ξ 1 [\xi_1, \xi_2] = \xi_1 \xi_2 - \xi_2 \xi_1 [ξ1,ξ2]=ξ1ξ2−ξ2ξ1 或者 [ η 1 , η 2 ] = [ ω 1 × ω 2 ω 1 × v 2 − ω 2 × v 1 ] [\boldsymbol{\eta}_1, \boldsymbol{\eta}_2] = \begin{bmatrix} \boldsymbol{\omega}_1 \times \boldsymbol{\omega}_2 \\ \boldsymbol{\omega}_1 \times \boldsymbol{v}_2 - \boldsymbol{\omega}_2 \times \boldsymbol{v}_1 \end{bmatrix} [η1,η2]=[ω1×ω2ω1×v2−ω2×v1] |
| 指数映射 | exp ( ξ ) = [ exp ( [ ω ] × ) J v 0 T 1 ] J = sin θ θ I + ( 1 − sin θ θ ) a a T + 1 − cos θ θ [ a ] × \exp({\xi}) = \begin{bmatrix} \exp([\boldsymbol{\omega}]_\times) & J\boldsymbol{v} \\ \mathbf{0}^T & 1 \\ \end{bmatrix}\\J=\frac{\sin\theta}{\theta}I + (1 - \frac{\sin\theta}{\theta}){a}{a^T} + \frac{1 - \cos\theta}{\theta} [a]_\times exp(ξ)=[exp([ω]×)0TJv1]J=θsinθI+(1−θsinθ)aaT+θ1−cosθ[a]× |
| 对数映射 | θ = arccos ( tr ( R ) − 1 2 ) , R a = a , t = J v \theta = \arccos\left( \frac{\operatorname{tr}(R) - 1}{2} \right),Ra = a,\boldsymbol{t} = J\boldsymbol{v} θ=arccos(2tr(R)−1),Ra=a,t=Jv |
注意可能符号与书上的符号略有差异,读者可以自行对照参考。
另外,笔者也想说一点内容之外的感受。除非具有相当的抽象能力,第一次接触到像李群和李代数这样的知识是很难理解到位的,因为你完全没有应用这些知识的场景,再怎么认真看书,也不过是泛泛而过。在这种情况下,不如好好推导一遍其中的原理,举一些实际的例子来加深映像。另外,这些数学知识既高深又抽象(笔者大概翻阅了一下《李理论》的相关知识,本文的这些推导在行家面前估计不值一哂),我们也不用过多去纠结,主打一个能自己说服自己即可。如果读者只是像我一样的普通人,可能需要在以后的应用和实践中来更深入地理解这些知识了;目前我们需要做的,就是不要排斥这个新的工具,然后理解它,利用它——真理之道,就在其中。
相关文章:
)
详解SLAM中的李群和李代数(中)
1 概述 在上一篇文章《详解SLAM中的李群和李代数(上)》中,我们已经通过对李群求导引出了李代数。在这篇文章中,我们就系统总结一下李代数的相关知识。 2 李代数 2.1 定义 李代数是一个向量空间 g \mathfrak{g} g与一个二元运算…...

Jenkins企业级实战
目标 在Windows操作系统上使用Jenkins完成代码的自动拉取、编译、打包、发布工作。 实施 1.安装Java开发工具包(JDK) Jenkins是基于Java的应用程序,因此需要先安装JDK。可以从Oracle官网或OpenJDK下载适合的JDK版本。推荐java17版本&#x…...

uniapp-商城-52-后台 商家信息(商家信息数据,云对象使用)
1、概述 已经通过好几个篇幅来说明商家信息,包括logo、商家名称,地址,电话以及商家简介。通过表单组件和标签,以及我们的文件上传标签,都做了说明。(logo上传,用的文件上传组件是上传到公共的数…...

MySQL 索引设计宝典:原理、原则与实战案例深度解析
目录 前言第一章:索引设计的基础原则 (知其然,更要知其所以然)第二章:实战案例:电商订单系统的索引设计第三章:索引设计的实践流程总结结语 🌟我的其他文章也讲解的比较有趣😁,如果喜…...
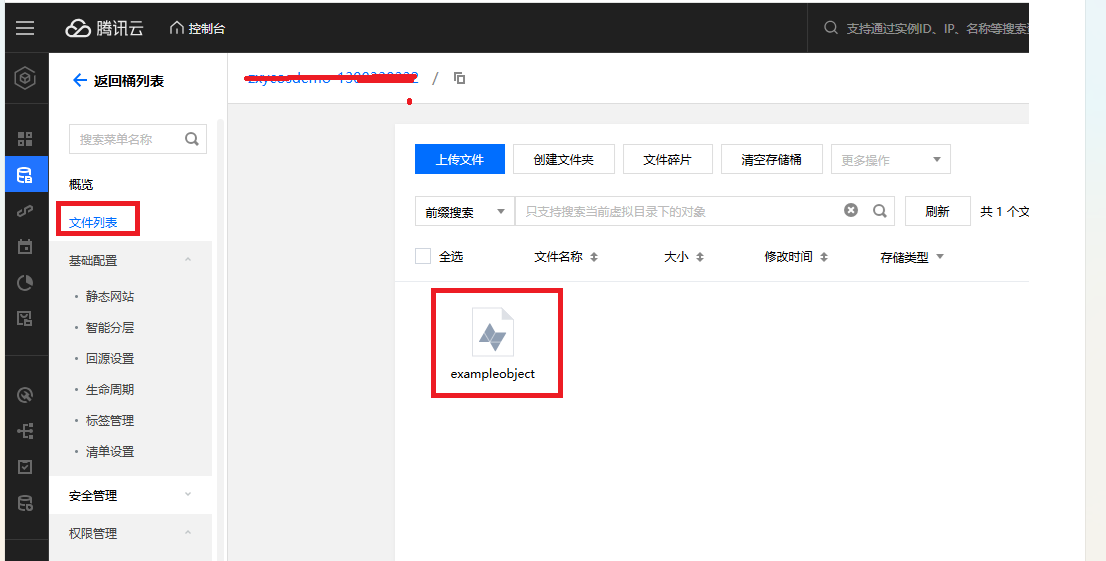
C#上传文件到腾讯云的COS
测试环境: vs2022 .net 6控制台应用程序 测试步骤如下: 1 添加子用户,目前是为了拿到secretId和secretKey,打开添加子用户界面链接:https://console.cloud.tencent.com/cam 并为子用户添加API 密钥 2 通过链接htt…...

java的Stream流处理
Java Stream 流处理详解 Stream 是 Java 8 引入的一个强大的数据处理抽象,它允许你以声明式方式处理数据集合(类似于 SQL 语句),支持并行操作,提高了代码的可读性和处理效率。 一、Stream 的核心概念 1. 什么是 Str…...

C PRIMER PLUS——第9节:动态内存分配、存储类别、链接和内存管理
目录 1.动态内存分配 1.1 malloc 函数 1.2 calloc 函数 1.3 realloc 函数 1.4 free 函数 1.5常见错误 1.6综合例题 2.C语言的内存结构 3.存储类别 3.1作用域(Scope) 3.2链接(Linkage) 3.3存储期(Storage Du…...

作业...
基础配置 RI R2 R3 R4 R5 例如R1 BGP配置 1,R1和R2之间使用直连接口IP地址来建立EBGP对等体关系 2、R2、R3、R4之间配置OSPF协议,保证各设备之间的网络互通,且通过重发布的方式发布路由 查看R2、R3、R4的OSPF路由表: \ R2、R3、R4使用环…...
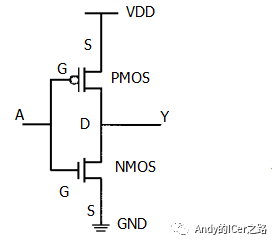
IC ATE集成电路测试学习——电流测试的原理和方法
电流测试 我们可以通过电流来判断芯片的工作状态时,首先先了解下芯片的电流是如何产生的。 静态电流 理论上,CMOS结构的芯片静态时几乎不耗电 CMOS基本结构:Pmos Nmos 串联当逻辑电平稳定时: ➜ 要么Pmos导通,Nmo…...
)
redis数据结构-03 (HMSET、HGET、HGETALL)
Redis 哈希介绍:HMSET、HGET、HGETALL Redis 哈希是一种强大的数据结构,允许您在单个键内存储字段值对的集合。它们对于表示对象、配置或任何可以自然分组到字段中的数据非常有用。本课将向您介绍使用 Redis 哈希的基本命令: HMSET 、 HGET …...

2025年01月09日德美医疗前端面试
目录 vue2 的双向绑定的原理vue3 的双向绑定原理vue 的生命周期vue 子组件为何不能修改父组件的值js delete 删除数组的某一个值会怎么样vue 和 react 的 diff 算法什么是闭包原型链this指向 vue2 的双向绑定的原理 以下是 Vue 2 双向绑定的原理: 1. 核心概念 …...

快速理解动态代理
什么是动态代理(Java核心技术卷1的解释) 动态代理是一种运行时生成代理对象的技术,其本质是通过字节码增强在不修改原始类代码的前提下,动态拦截并扩展目标对象的行为。它通过代理对象对原始方法的调用进行拦截,并在方法执行前后注入自定义逻…...

实战演练:用 AWS Lambda 和 API Gateway 构建你的第一个 Serverless API
实战演练:用 AWS Lambda 和 API Gateway 构建你的第一个 Serverless API 理论千遍,不如动手一遍!在前面几篇文章中,我们了解了 Serverless 的概念、FaaS 的核心原理以及 BaaS 的重要作用。现在,是时候把这些知识运用起来,亲手构建一个简单但完整的 Serverless 应用了。 …...

spark算子介绍
目录 1. 转换算子(Transformation)1.1 常用转换算子 2. 行动算子(Action)2.1 常用行动算子 3. 转换算子与行动算子的区别4. 示例代码5. 总结 在Spark中,算子(Operator)是对数据集(RD…...

AugmentCode 非常昂贵的新定价
AugmentCode 现在的价格比 Cursor 和 Windsurf 的总和还要贵。 AugmentCode 曾是我开发工作流程的常用工具。出乎意料的是,他们改变了定价结构,让开发者们震惊不已。 原来的30 美元月费已经增长为50 美元月费,这是一个67%的增长。 改变我看法的不仅仅是价格上涨,还有他…...

前端面试2
1. 面试准备 1. 建立自己的知识体系 思维导图ProcessOn框架Vue elementUI自查 https://zh.javascript.info/ 借鉴 https://juejin.cn/post/6844904103504527374http://conardli.top/blog/article/https://github.com/mqyqingfeng/Bloghttp://47.98.159.95/my_blog/#html 2.技能…...
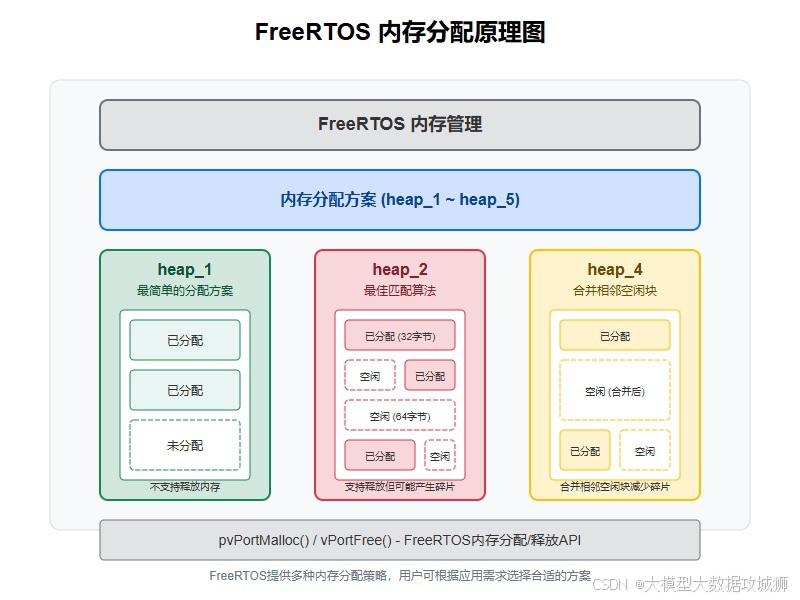
大疆卓驭嵌入式面经及参考答案
FreeRTOS 有哪 5 种内存管理方式? heap_1.c:这种方式简单地在编译时分配一块固定大小的内存,在整个运行期间不会进行内存的动态分配和释放。它适用于那些对内存使用需求非常明确且固定,不需要动态分配内存的场景,优点是…...
)
RAID磁盘阵列的概念(自用留档)
概念 RAID磁盘阵列是由若干个磁盘组成的磁盘组。 磁盘组可以恢复意外丢失的数据,保证了数据的安全性。 种类 根据实际情况的不同,RAID有若干种,以一个具有三块硬盘的硬盘组为例: RAID 0:将文件拆分成三份分别放到三…...
享元模式)
设计模式简述(十八)享元模式
享元模式 描述基本组件使用 描述 当内存中存在大量类似的对象时,可以考虑使用享元模式减少整体内存占用。 可以将相同的部分和不同的部分进行拆分,以达到多个对象共享相同部分内存的目的。 基本组件 通常享元对象通过共享的属性映射一个享元对象。 公…...

架构进阶:74页数据架构设计总体规划方案【附全文阅读】
本文讨论了数据资源规划在信息化战略规划中的重要性,详细阐述了数据资源规划的方法与过程,包括系统架构、业务能力模型、数据架构等。 文章指出,数据资源规划需要梳理企业级数据模型,明确数据分布和流向,建立统一的数据…...

情书大全v3.0.1
《情书大全》是一款致力于情书写作的手机应用程序,内置了丰富的情书范本及定制化服务。用户无论是想要倾诉爱意、交流友情还是传递亲情,都能在这款应用中寻得合适的情书样本。用户还可以根据自己的需求对模板进行编辑和调整,轻松创作出感人至…...

基于OpenCV的人脸识别:LBPH算法
文章目录 引言一、概述二、代码实现1. 代码整体结构2. 导入库解析3. 训练数据准备4. 标签系统5. 待识别图像加载6. LBPH识别器创建7. 模型训练8. 预测执行9. 结果输出 三、 LBPH算法原理解析四、关键点解析五、改进方向总结 引言 人脸识别是计算机视觉领域的一个重要应用&…...

鸿蒙 使用动画 简单使用
鸿蒙 使用动画 简单使用 动画就两个,属性动画和转场动画 属性动画只是组件的属性发生变化,而转场动画是指对将要出现或消失的组件做动画,而文档的其他动画只是给这两个动画效果锦上添花罢了 这篇文章简单介绍这两个动画,其他的…...

MySQL数据库迁移SQL语句指南
MySQL数据库迁移SQL语句指南 一、基础迁移方法 1. 使用mysqldump进行全量迁移 -- 导出源数据库(在命令行执行) mysqldump -u [源用户名] -p[源密码] --single-transaction --routines --triggers --events --master-data2 [数据库名] > migration…...

arcgis和ENVI中如何将数据输出为tif
一、arcgis中转换为tif 右键图层: Data -> Export Data, 按照图示进行选择,选择tiff格式导出即可,还可以选择其他类型的格式,比如envi。 二、 ENVI中转换为tif File -> Save As -> Save As (ENVI, NITF, TIFF, DTED) …...

RagFlow 完全指南(一):从零搭建开源大模型应用平台(Ollama、VLLM本地模型接入实战)
文章目录 1. 相关资源2. 核心特性3. 安装与部署3.1 环境准备3.2 部署RagFlow3.3 更新RagFlow3.4 系统配置 4. 接入本地模型4.1 接入 Ollama 本地模型4.1.1 步骤4.1.2 常见问题 4.2 接入 VLLM 模型 5. 应用场景6. 总结 1. 相关资源 官网GitHub文档中心 2. 核心特性 …...

计算机网络 4-2-1 网络层(IPv4)
2 IPv4分组 各协议之间的关系 IP协议(Internet Protocol, 网际协议)是互联网的核心! ARP协议用于查询同一网络中的<主机IP地址,MAC地址>之间的映射关系 ICMP协议用于网络层实体之间相互通知“异常事件” IGMP协议用于实现IP组播 2.1 结构<首…...

Python赋能自动驾驶:如何打造高效的环境感知系统
Python赋能自动驾驶:如何打造高效的环境感知系统 大家好,我是 Echo_Wish,今天我们来聊聊自动驾驶里的“眼睛”——环境感知系统,以及如何用 Python 实现它。 自动驾驶的核心目标是让车辆在没有人工干预的情况下安全行驶,而要做到这一点,环境感知系统必须实时获取并理解…...
)
ST表(稀疏表)
对ST表进行一个简单的总结,它可以实现O(1)的静态区间查询,可以适用于查询操作频繁但数据不修改的场景 题目来源 https://www.luogu.com.cn/problem/P3865 题目介绍 给定一个长度为 N 的数列,和 M 次询问,求出每一次询问的区间…...

Java常用类-比较器
目录 一、为什么需要比较器?二、核心差异速记表三、Comparable:对象自带的 “默认规则”1. 核心作用2. 源码定义3. 实战:给Student类加默认规则4. 源码验证(以Integer为例) 四、Comparator:临时的 “外部规…...
