【匹配】Needleman–Wunsch
Needleman-Wunsch
文章目录
- Needleman-Wunsch
- 1. 算法介绍
- 2. 公式及原理
- 3. 伪代码
1. 算法介绍
-
背景与目标
Needleman–Wunsch 算法由 Saul B. Needleman 和 Christian D. Wunsch 于1970年提出,是用于生物序列(如蛋白质或 DNA)全局比对(global alignment)的经典动态规划方法。其核心目标是:在允许插入、缺失(gap)和错配的情况下,找到两条序列从头到尾的最优比对,使得总体得分最大。
-
应用场景
- 两条全长蛋白质序列或 DNA 序列的全局比对
- 构建进化距离矩阵、聚类与系统发生学分析
- 作为后续更复杂比对(如多序列比对、局部比对)的基础
-
核心思路
- 构建一个大小为 ( m + 1 ) × ( n + 1 ) (m+1)\times(n+1) (m+1)×(n+1) 的积分得分矩阵 F F F,其中 m , n m,n m,n 分别为两序列长度;
- 以线性或 affine gap penalty 设定缺口代价;
- 通过动态规划递推填表,计算从起点到任意 ( i , j ) (i,j) (i,j) 的最优比对得分;
- 从右下角回溯(traceback),还原最佳全局比对路径。
2. 公式及原理
2.1 符号与评分函数
-
序列 A = a 1 a 2 ⋯ a m \mathbf{A}=a_1a_2\cdots a_m A=a1a2⋯am, B = b 1 b 2 ⋯ b n \mathbf{B}=b_1b_2\cdots b_n B=b1b2⋯bn。
-
设定匹配/错配得分函数:
s ( a i , b j ) = { + α , a i = b j ( match ) − β , a i ≠ b j ( mismatch ) s(a_i,b_j) = \begin{cases} +\alpha, & a_i = b_j \quad(\text{match})\\ -\beta, & a_i \neq b_j \quad(\text{mismatch}) \end{cases} s(ai,bj)={+α,−β,ai=bj(match)ai=bj(mismatch)
-
线性缺口惩罚:对于连续插入或删除长度为 k k k,惩罚为 − k ⋅ d -k\cdot d −k⋅d。
2.2 初始化
F [ 0 , 0 ] = 0 , F [ i , 0 ] = − i ⋅ d ( i = 1 , … , m ) , F [ 0 , j ] = − j ⋅ d ( j = 1 , … , n ) . F[0,0] = 0,\quad F[i,0] = -i\cdot d\quad (i=1,\dots,m),\quad F[0,j] = -j\cdot d\quad (j=1,\dots,n). F[0,0]=0,F[i,0]=−i⋅d(i=1,…,m),F[0,j]=−j⋅d(j=1,…,n).
2.3 递推公式
对任意 1 ≤ i ≤ m 1\le i\le m 1≤i≤m, 1 ≤ j ≤ n 1\le j\le n 1≤j≤n,
F [ i , j ] = max { F [ i − 1 , j − 1 ] + s ( a i , b j ) , F [ i − 1 , j ] − d , F [ i , j − 1 ] − d . F[i,j] = \max\!\begin{cases} F[i-1,\,j-1] + s(a_i,b_j),\\ F[i-1,\,j] - d,\\ F[i,\,j-1] - d. \end{cases} F[i,j]=max⎩ ⎨ ⎧F[i−1,j−1]+s(ai,bj),F[i−1,j]−d,F[i,j−1]−d.
2.4 回溯(Traceback)
从 ( i , j ) = ( m , n ) (i,j)=(m,n) (i,j)=(m,n) 开始:
- 如果 F [ i , j ] = F [ i − 1 , j − 1 ] + s ( a i , b j ) F[i,j] = F[i-1,j-1] + s(a_i,b_j) F[i,j]=F[i−1,j−1]+s(ai,bj),则对齐 a i a_i ai 与 b j b_j bj,移动 ( i , j ) → ( i − 1 , j − 1 ) (i,j)\to(i-1,j-1) (i,j)→(i−1,j−1);
- 否则若 F [ i , j ] = F [ i − 1 , j ] − d F[i,j] = F[i-1,j] - d F[i,j]=F[i−1,j]−d,则对齐 a i a_i ai 与 gap,移动 ( i , j ) → ( i − 1 , j ) (i,j)\to(i-1,j) (i,j)→(i−1,j);
- 否则对齐 gap 与 b j b_j bj,移动 ( i , j ) → ( i , j − 1 ) (i,j)\to(i,j-1) (i,j)→(i,j−1)。
直到回到 ( 0 , 0 ) (0,0) (0,0)。
3. 伪代码
# 输入
# A[1..m], B[1..n]: 待比对序列
# s(a,b): 匹配得分函数
# d: 线性 gap penalty
# 输出
# aligned_A, aligned_B: 两个同长的对齐序列function NeedlemanWunsch(A, B, s, d):m ← length(A); n ← length(B)# 1) 初始化矩阵 F 大小 (m+1)x(n+1)for i in 0..m:F[i,0] ← -i * dfor j in 0..n:F[0,j] ← -j * d# 2) 填表for i in 1..m:for j in 1..n:match ← F[i-1,j-1] + s(A[i], B[j])delete ← F[i-1,j] - dinsert ← F[i, j-1] - dF[i,j] ← max(match, delete, insert)# 3) 回溯还原比对i ← m; j ← naligned_A, aligned_B ← empty stringswhile i>0 or j>0:if i>0 and j>0 and F[i,j] == F[i-1,j-1] + s(A[i],B[j]):aligned_A.prepend(A[i])aligned_B.prepend(B[j])i ← i-1; j ← j-1else if i>0 and F[i,j] == F[i-1,j] - d:aligned_A.prepend(A[i])aligned_B.prepend('-')i ← i-1else:aligned_A.prepend('-')aligned_B.prepend(B[j])j ← j-1return aligned_A, aligned_B
- 时间复杂度: O ( m × n ) O(m \times n) O(m×n)
- 空间复杂度: O ( m × n ) O(m \times n) O(m×n)(可用带回溯链的 Hirschberg 算法降到 O ( m + n ) O(m+n) O(m+n))
相关文章:

【匹配】Needleman–Wunsch
Needleman-Wunsch 文章目录 Needleman-Wunsch1. 算法介绍2. 公式及原理3. 伪代码 1. 算法介绍 背景与目标 Needleman–Wunsch 算法由 Saul B. Needleman 和 Christian D. Wunsch 于1970年提出,是用于生物序列(如蛋白质或 DNA)全局比对&#x…...

崩坏星穹铁道 3.3 版本前瞻活动攻略:在黎明升起时坠落
《崩坏星穹铁道》3.3 版本 “在黎明升起时坠落” 将于 5 月 21 日正式上线。本次版本更新内容丰富,新角色、新地图、新活动和新周本 BOSS 等精彩内容,等待开拓者们前去体验。下面就为大家带来 3.3 版本的前瞻活动攻略。 一、新角色与卡池 1.上半卡池&am…...

OneNote内容太多插入标记卡死的解决办法
OneNote内容太多插入标记卡死的解决办法 针对平板电脑的OneNote用户适合此类情况: 当向电脑导入几百页pdf可以正常使用,唯独插入标记的时候OneNote直接罢工,只能关闭。关闭时还可能会出现0x000000fxxxxx的错误。 注:仅对于平板…...

fpga系列 HDL : Microchip FPGA开发软件 Libero Soc 安装 license申请
启动 注册账号:https://login.microchip.com/申请免费许可:https://www.microchipdirect.com/fpga-software-products C:\Windows\System32>vol驱动器 C 中的卷是 Windows卷的序列号是 ****-****为“D:\Microsemi\License.dat”创建环境变量“LM_LICE…...

极简主义现代商务风格PPT模版6套一组分享下载
现代商务风格PPT模版下载https://pan.quark.cn/s/12fbc52124d9 第一张PPT模版,简约风,橄榄绿背景,黑色竖条装饰,文字有中英文标题和占位符。需要提取关键元素:简约、橄榄绿、对称布局、占位文本的位置。 风格&#…...
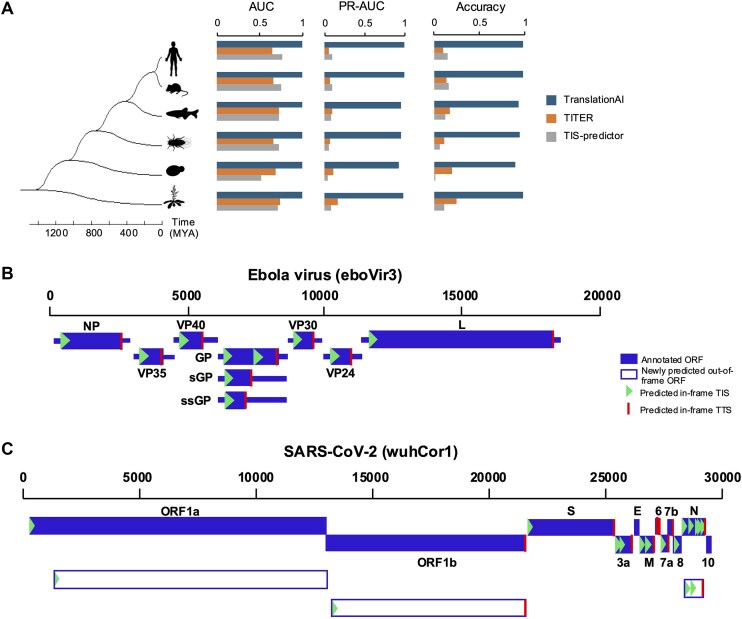
解码生命语言:深度学习模型TranslationAI揭示RNA翻译新规则
RNA翻译是基因表达的核心环节,其精确调控依赖于翻译起始位点(TIS)和终止位点(TTS)的准确识别。传统方法依赖于简单的经验规则(如Kozak序列或最长开放阅读框ORF),但忽略了RNA结构、顺…...

重磅发布!OpenAI 推出最新模型 GPT-4.1 系列!
今日凌晨,OpenAI宣布开放全新模型GPT-4.1,并于即日起在ChatGPT中投入使用。 超长上下文与卓越编码能力 GPT-4.1作为OpenAI的最新模型,支持长达100万tokens的上下文,是OpenAI首次发布的长窗口模型。相较于前代,GPT-4.1…...

配置别名路径 @
CRA本身把webpack配置包装到了黑盒里无法直接修改,需要借助一个插件 - craco 1. 路径解析配置(Webpack)-- craco 插件 把 / 解析为 src/ 配置步骤: 1.安装 craco npm i -D craco/craco 2. 项目根目录下创建配置文件 craco.co…...

给视频加一个动画。
为什么要给视频加一个动画? 很完整的视频也就是从短动画开始的。遮盖住LOG用。 C:\Users\Sam\Desktop\desktop\startup\workpython\ocr Lottie.py import subprocessdef run_ffmpeg(cmd):print("Running:", " ".join(cmd))subprocess.run(cm…...

sqli-labs靶场第七关——文件导出注入
一:目标 通过sql注入将php代码写入网站目录,通过这个php文件执行命令 二:确认前置条件 %secure_file_priv% 首先我们需要Mysql是否允许导出文件 先尝试在网页中sql注入,检查导出权限 ?id1)) union select 1,secure_file_pr…...
)
uniapp 弹窗封装(上、下、左、右、中五个方位)
无脑复制即可!!! <template><view><viewv-if"mask"class"tui-drawer-mask":class"{ tui-drawer-mask_show: visible }":style"{ zIndex: maskZIndex }"tap"handleMaskClick&qu…...

解密企业级大模型智能体Agentic AI 关键技术:MCP、A2A、Reasoning LLMs-docker MCP解析
解密企业级大模型智能体Agentic AI 关键技术:MCP、A2A、Reasoning LLMs-docker MCP解析 这里面有很重要的原因其中一个很其中一个原因是因为如果你使用docker的方式,你可以在虚拟环境下就类似于这个沙箱的这个机制可以进行隔离。这对于安全,…...
基本概念)
Modern C++(一)基本概念
1、基本概念 1.1、注释 注释在翻译阶段3会被替换为单个空白字符从程序中移除 1.2、名字与标识符 标识符是一个由数字、下划线、大小写字符组成的任意长度序列。有效的标识符首个字符必须是以A-Z、a-z、下划线开头,。有效的标识符其他字符可以是0-9、A-Z、a-z、下…...

OpenCV图像旋转原理及示例
OpenCV计算机视觉开发实践:基于Qt C - 商品搜索 - 京东 图像旋转是数字图像处理的一个非常重要的环节,是图像的几何变换手法之一。图像旋转算法是图像处理的基础算法。在数字图像处理过程中,经常要用到旋转,例如在进行图像扫描时…...

LLM Text2SQL NL2SQL 实战总结
目录 尽量全面的描述表的功能 尽量全面的描述字段的功能 适当放弃意义等价的字段 放弃业务上无用的字段 对于LLM来说,由于它没有什么行业经验,所以我们需要尽可能的给予它恰当的“背景信息”,才能使它更好的工作。所谓恰当,不是越多越好,因为太多的信息会消耗掉LLM的可…...

k8s 中使用 Service 访问时NetworkPolicy不生效问题排查
背景 针对一个服务如下NetworkPolicy, 表示只有n9e命名空间的POD才能访问 k8s-man 服务 kind: NetworkPolicy apiVersion: networking.k8s.io/v1 metadata:name: k8s-mannamespace: n9elabels:app: k8s-manversion: v1 spec:podSelector:matchLabels:app: k8s-manversion: v1…...

【实战篇】数字化打印——打印部署管理接口开发
前言 前面的章节已经介绍了打印管理模块的主要界面设计,本篇介绍用myBuilder开发界面接口,实现最终的功能。 1. 配置打印应用菜单 首先配置挂载好模块菜单 让菜单点击能访问到对应的页面 2. 打印部署管理数据表详细设计 以下是打印部署管理的数据表字…...

MacOS Python3安装
python一般在Mac上会自带,但是大多都是python2。 python2和python3并不存在上下版本兼容的情况,所以python2和python3可以同时安装在一台设备上,并且python3的一些语法和python2并不互通。 所以在Mac电脑上即使有自带python,想要使…...

磁盘I/O瓶颈排查:面试通关“三部曲”心法
想象一下,你就是线上系统的“交通调度总指挥”,服务器的磁盘是所有数据进出的“核心枢纽港口”。当这个“港口”突然拥堵不堪,卡车(数据请求)排起长龙,进不去也出不来,整个系统的“物流”&#…...

idea启动报错:java: 警告: 源发行版 11 需要目标发行版 11(亲测解决)
引起原因 idea的jdk没有替换干净 1.配置project file–Project Structrue–Project 2.配置Modules-Sources file–Project Structrue–Modules-Sources 改为jdk11 3.配置Modules-Dependencies file–Project Structrue–Modules-Dependencies...

树莓派4 yolo 11l.pt性能优化后的版本
树莓派4 使用 Picamera2 拍摄图像,然后通过 YOLO11l.pt 进行目标检测,并在实时视频流中显示结果。但当前的代码在运行时可能会比较卡顿,主要原因包括: picam2.capture_array() 是一个较慢的操作;YOLO 推理可能耗时较长…...

鸿蒙OSUniApp开发支持多语言的国际化组件#三方框架 #Uniapp
使用UniApp开发支持多语言的国际化组件 在全球化的今天,一个优秀的应用往往需要支持多种语言以满足不同地区用户的需求。本文将详细讲解如何在UniApp框架中实现一套完整的国际化解决方案,从而轻松实现多语言切换功能。 前言 去年接手了一个面向国际市场…...

国产数据库工具突围:SQLynx如何解决Navicat的三大痛点?深度体验报告
引言:Navicat的"中国困境" 当开发者面对达梦数据库的存储过程调试,或是在人大金仓中处理复杂查询时,Navicat突然变得力不从心——这不是个例。 真实痛点:某政务系统迁移至OceanBase后,开发团队发现Navicat无…...

《Adversarial Sticker: A Stealthy Attack Method in the Physical World》论文分享(侵删)
原文链接:Adversarial Sticker: A Stealthy Attack Method in the Physical World | IEEE Journals & Magazine | IEEE Xplore author{Xingxing Wei and Ying Guo and Jie Yu} 摘要 为了评估深度学习在物理世界中的脆弱性,最近的工作引入了对抗补丁…...

Python生成器:高效处理大数据的秘密武器
生成器概述 生成器是 Python 中的一种特殊迭代器,通过普通函数的语法实现,但使用 yield 语句返回数据。生成器自动实现了 __iter__() 和 __next__() 方法,因此可以直接用于迭代。生成器的核心特点是延迟计算(lazy evaluation&…...

React Native/Flutter 原生模块开发
以下是关于 React Native 和 Flutter 原生模块开发的基本知识点总结: 一、核心概念对比 维度React NativeFlutter架构基础JavaScriptCore/Hermes + Bridge/TurboModulesDart VM + Skia引擎原生交互方式Native Modules + Native UI ComponentsPlatform Channels + Platform Vie…...

嵌入式STM32学习——继电器
继电器模块引脚说明 VCC(): 供电正极。连接此引脚到电源(通常是直流电源),以提供继电器线圈所需的电流。 GND(-): 地。连接此引脚到电源的负极或地。 IN(或…...

从基础到实习项目:C++后端开发学习指南
在当今技术快速迭代的背景下,后端开发作为软件工程的核心支柱持续发挥着关键作用。C凭借其卓越的性能表现和系统级控制能力,依然是构建高性能后端服务的首选语言之一。本文将系统性地解析现代C后端开发的核心技术体系,包括从语言特性精要到架…...

AI软件汇总与功能解析:赋能未来的智能工具库
人工智能(AI)技术的快速发展催生了大量功能强大的软件工具,覆盖自然语言处理、计算机视觉、数据分析、自动化决策等多个领域。本文将汇总当前主流的AI软件,并解析其核心功能与应用场景,为企业和开发者提供参考指南。 一…...

Xinference推理框架
概述 GitHub,官方文档。 核心优势 性能优化:通过vLLM、SGLang等引擎实现低延迟推理,吞吐量提升2-3倍;企业级支持:支持分布式部署、国产硬件适配及模型全生命周期管理;生态兼容:无缝对接LangC…...
