基于 Python 的界面程序复现:标准干涉槽型设计计算及仿真
基于 Python 的界面程序复现:标准干涉槽型设计计算及仿真
在工业设计与制造领域,刀具的设计与优化是提高生产效率和产品质量的关键环节之一。本文将介绍如何使用 Python 复现一个用于标准干涉槽型设计计算及仿真的界面程序,旨在帮助工程师和研究人员更好地理解和优化刀具设计。
项目背景
在刀具制造过程中,干涉槽型的设计对于刀具的性能和寿命具有重要影响。传统的设计方法往往依赖于经验公式和手工计算,这种方式不仅效率低下,而且容易出错。随着计算机技术的发展,利用计算机辅助设计(CAD)和计算机辅助工程(CAE)工具进行刀具设计已成为趋势。

本文要复现的界面程序如图所示,来自某论文的一张图片,该程序用于标准干涉槽型的设计计算及仿真。通过该程序,用户可以输入刀具的几何参数和工艺参数,程序将自动计算相关的磨削参数、法向刃宽等,并以图形化的方式显示刀具的槽型。
界面程序开发
技术选型
为了实现上述功能,我们选择使用 Python 语言,并结合以下库进行开发:
tkinter:Python 的标准 GUI 库,用于创建图形用户界面。matplotlib:一个强大的绘图库,用于在界面中显示刀具的槽型图形。
程序结构设计
整个界面程序的设计遵循模块化原则,主要分为以下几个部分:
- 参数输入部分:用户可以在此输入刀具的几何参数(如直径、齿数、螺旋角等)和工艺参数(如砂轮半径、角度等)。
- 图形显示部分:用于实时显示刀具的槽型图形,帮助用户直观地了解设计结果。
- 计算与仿真部分:根据用户输入的参数,计算相关的磨削参数和刀具性能指标,并提供仿真功能。
代码实现
以下是界面程序的核心代码实现:
import tkinter as tk
from tkinter import ttk
import matplotlib.pyplot as plt
from matplotlib.figure import Figure
from matplotlib.backends.backend_tkagg import FigureCanvasTkAgg
from matplotlib.patches import Circleclass App:def __init__(self, root):self.root = rootself.root.title("标准干涉槽型设计计算及仿真界面程序")# 初始化参数字典self.parameters = {"直径 d(mm)": 10.00,"齿数 Nf": 4,"螺旋角 beta(°)": 35.0,"槽前角 gama(°)": 12.0,"芯厚 Wt(mm)": 6.00,"半径 Rw(mm)": 75.00,"角度 theta(°)": 70.00,"法向刃宽 lf(mm)": 1.000,"安装角 epsilon(°)": None,"轴间距 A0(mm)": None,"端面偏距 e(mm)": None}# 创建左侧参数输入部分self.create_parameter_section()# 创建中间图形显示部分self.create_graph_section()# 创建右侧步骤按钮部分self.create_step_section()def create_parameter_section(self):# 刀具结构设计参数self.tool_frame = ttk.LabelFrame(self.root, text="刀具结构设计参数")self.tool_frame.grid(row=0, column=0, padx=10, pady=10, sticky="w")parameters = ["直径 d(mm)", "齿数 Nf", "螺旋角 beta(°)", "槽前角 gama(°)", "芯厚 Wt(mm)"]self.entries_tool = {}for i, param in enumerate(parameters):ttk.Label(self.tool_frame, text=param).grid(row=i, column=0, padx=5, pady=5, sticky="w")entry = ttk.Entry(self.tool_frame)entry.insert(0, str(self.parameters[param]))entry.grid(row=i, column=1, padx=5, pady=5, sticky="w")entry.bind("<Return>", lambda e, p=param: self.update_parameter(p, entry.get()))self.entries_tool[param] = entry# 砂轮结构及位置参数self.wheel_frame = ttk.LabelFrame(self.root, text="砂轮结构及位置参数")self.wheel_frame.grid(row=1, column=0, padx=10, pady=10, sticky="w")parameters = ["半径 Rw(mm)", "角度 theta(°)"]self.entries_wheel = {}for i, param in enumerate(parameters):ttk.Label(self.wheel_frame, text=param).grid(row=i, column=0, padx=5, pady=5, sticky="w")entry = ttk.Entry(self.wheel_frame)entry.insert(0, str(self.parameters[param]))entry.grid(row=i, column=1, padx=5, pady=5, sticky="w")entry.bind("<Return>", lambda e, p=param: self.update_parameter(p, entry.get()))self.entries_wheel[param] = entry# 安装参数和刀宽self.installation_frame = ttk.LabelFrame(self.root, text="安装参数和刀宽")self.installation_frame.grid(row=2, column=0, padx=10, pady=10, sticky="w")parameters = ["法向刃宽 lf(mm)", "安装角 epsilon(°)", "轴间距 A0(mm)", "端面偏距 e(mm)"]self.entries_installation = {}for i, param in enumerate(parameters):ttk.Label(self.installation_frame, text=param).grid(row=i, column=0, padx=5, pady=5, sticky="w")entry = ttk.Entry(self.installation_frame)entry.insert(0, str(self.parameters[param] if self.parameters[param] is not None else ""))entry.grid(row=i, column=1, padx=5, pady=5, sticky="w")if param in ["安装角 epsilon(°)", "轴间距 A0(mm)", "端面偏距 e(mm)"]:entry.config(state='readonly')self.entries_installation[param] = entrydef create_graph_section(self):self.graph_frame = ttk.LabelFrame(self.root, text="图形显示")self.graph_frame.grid(row=0, column=1, rowspan=3, padx=10, pady=10, sticky="nsew")# 创建一个简单的图形显示区域self.fig = Figure(figsize=(5, 5), dpi=100)self.ax = self.fig.add_subplot(111)self.ax.set_xlim(-10, 10)self.ax.set_ylim(-10, 10)self.ax.grid(True)# 初始化时绘制两个圆self.draw_initial_circles()# 创建一个Canvas,用于显示图形self.canvas = FigureCanvasTkAgg(self.fig, master=self.graph_frame)self.canvas.get_tk_widget().pack(fill=tk.BOTH, expand=True)def draw_initial_circles(self):# 清除之前的图形,但保留坐标轴self.ax.clear()self.ax.set_xlim(-10, 10)self.ax.set_ylim(-10, 10)self.ax.grid(True)# 绘制两个圆outer_radius = self.parameters["直径 d(mm)"] / 2inner_radius = self.parameters["芯厚 Wt(mm)"] / 2outer_circle = Circle((0, 0), outer_radius, fill=False, color='blue')inner_circle = Circle((0, 0), inner_radius, fill=False, color='red')self.ax.add_patch(outer_circle)self.ax.add_patch(inner_circle)self.canvas.draw()def draw_slot_profile(self):# 在现有图形上绘制槽型# 这里只是一个示例,实际槽型计算需要根据具体需求实现self.ax.plot([1, 2, 3, 4], [1, 2, 3, 4], 'g-')self.canvas.draw()def create_step_section(self):self.step_frame = ttk.LabelFrame(self.root, text="步骤")self.step_frame.grid(row=0, column=2, rowspan=3, padx=10, pady=10, sticky="nsew")steps = ["step1 计算磨削参数", "step2 计算法向刀宽", "step3 显示刀具径向槽型", "step4 计算面积惯性矩"]self.buttons = []for i, step in enumerate(steps):button = ttk.Button(self.step_frame, text=step, command=lambda s=step: self.on_button_click(s))button.pack(fill=tk.X, padx=5, pady=5)self.buttons.append(button)def update_parameter(self, param, value):try:if param in ["齿数 Nf"]:self.parameters[param] = int(value)else:self.parameters[param] = float(value)# 更新参数字典后,重新绘制图形self.draw_initial_circles()except ValueError:print(f"Invalid value for {param}")def on_button_click(self, step):print(f"Button clicked: {step}")if step == "step1 计算磨削参数":self.calculate_grinding_parameters()elif step == "step3 显示刀具径向槽型":self.draw_slot_profile()def calculate_grinding_parameters(self):# 这里只是一个简单的示例,实际计算需要根据具体需求实现d = self.parameters["直径 d(mm)"]Nf = self.parameters["齿数 Nf"]beta = self.parameters["螺旋角 beta(°)"]lf = self.parameters["法向刃宽 lf(mm)"]# 计算安装角 epsilonepsilon = 45.0 # 示例计算# 计算轴间距 A0A0 = d * Nf / 2 # 示例计算# 计算端面偏距 ee = -d / (2 * Nf) # 示例计算# 更新参数字典self.parameters["安装角 epsilon(°)"] = epsilonself.parameters["轴间距 A0(mm)"] = A0self.parameters["端面偏距 e(mm)"] = e# 更新界面显示self.entries_installation["安装角 epsilon(°)"].config(state='normal')self.entries_installation["安装角 epsilon(°)"].delete(0, tk.END)self.entries_installation["安装角 epsilon(°)"].insert(0, str(epsilon))self.entries_installation["安装角 epsilon(°)"].config(state='readonly')self.entries_installation["轴间距 A0(mm)"].config(state='normal')self.entries_installation["轴间距 A0(mm)"].delete(0, tk.END)self.entries_installation["轴间距 A0(mm)"].insert(0, str(A0))self.entries_installation["轴间距 A0(mm)"].config(state='readonly')self.entries_installation["端面偏距 e(mm)"].config(state='normal')self.entries_installation["端面偏距 e(mm)"].delete(0, tk.END)self.entries_installation["端面偏距 e(mm)"].insert(0, str(e))self.entries_installation["端面偏距 e(mm)"].config(state='readonly')if __name__ == "__main__":root = tk.Tk()app = App(root)root.mainloop()
功能细节
参数输入
用户可以在界面的左侧输入刀具的几何参数和工艺参数。输入框支持实时更新,用户按下回车键后,程序会立即更新参数并重新绘制图形。
图形显示
中间的图形显示区域使用 matplotlib 绘制刀具的槽型。初始化时,根据用户输入的直径和芯厚绘制两个圆。用户可以通过点击“step3 显示刀具径向槽型”按钮,在现有图形上绘制槽型。
计算与仿真
右侧的步骤按钮提供了不同的计算和仿真功能:
- step1 计算磨削参数:计算安装角、轴间距和端面偏距,并将结果显示在对应的输入框中。
- step2 计算法向刀宽:计算法向刀宽(此功能需根据具体需求实现)。
- step3 显示刀具径向槽型:在图形显示区域绘制刀具的槽型。
- step4 计算面积惯性矩:计算刀具截面的面积惯性矩(此功能需根据具体需求实现)。
总结与展望
本文介绍的基于 Python 的标准干涉槽型设计计算及仿真界面程序,为刀具设计提供了一个直观、高效的工具。通过 tkinter 和 matplotlib 的结合,实现了参数输入、图形显示和计算仿真等功能。
未来的工作将集中在以下几个方面:
- 功能扩展:增加更多的计算和仿真功能,如法向刀宽和面积惯性矩的精确计算。
- 优化界面:进一步优化界面布局和交互体验,使其更加用户友好。
- 实际应用:将程序应用于实际的刀具设计和制造过程中,验证其有效性和实用性。
相关文章:

基于 Python 的界面程序复现:标准干涉槽型设计计算及仿真
基于 Python 的界面程序复现:标准干涉槽型设计计算及仿真 在工业设计与制造领域,刀具的设计与优化是提高生产效率和产品质量的关键环节之一。本文将介绍如何使用 Python 复现一个用于标准干涉槽型设计计算及仿真的界面程序,旨在帮助工程师和…...

c++成员函数返回类对象引用和直接返回类对象的区别
c成员函数返回类对象引用和直接返回类对象的区别 成员函数直接返回类对象(返回临时对象,对象拷贝) #include <iostream> class MyInt { public:int value;//构造函数explicit MyInt(int v0) : value(v){}//加法操作,返回对象副本&…...
:混合检索之rank_bm25库来实现词法搜索)
AGI大模型(20):混合检索之rank_bm25库来实现词法搜索
1 混合检索简介 混合搜索结合了两种检索信息的方法 词法搜索 (BM25) :这种传统方法根据精确的关键字匹配来检索文档。例如,如果您搜索“cat on the mat”,它将找到包含这些确切单词的文档。 基于嵌入的搜索(密集检索) :这种较新的方法通过比较文档的语义来检索文档。查…...
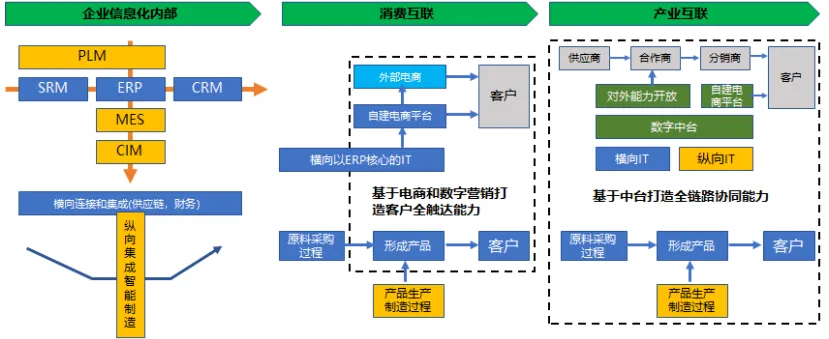
数字化转型- 数字化转型路线和推进
数字化转型三个阶段 百度百科给出的企业的数字化转型包括信息化、数字化、数智化三个阶段 信息化是将企业在生产经营过程中产生的业务信息进行记录、储存和管理,通过电子终端呈现,便于信息的传播与沟通。数字化通过打通各个系统的互联互通,…...

字体样式集合
根据您提供的字体样式列表,以下是分类整理后的完整字体样式名称(不含数量统计): 基础样式 • Regular • Normal • Plain • Medium • Bold • Black • Light • Thin • Heavy • Ultra • Extra • Semi • Hai…...

IP68防水Type-C连接器实测:水下1米浸泡72小时的生存挑战
IP68防水Type-C连接器正成为户外设备、水下仪器和高端消费电子的核心组件。其宣称的“1米水深防护”是否真能抵御长时间浸泡?我们通过极限实测,将三款主流品牌IP68防水Type-C连接器沉入1米盐水(模拟海水浓度)中持续72小时…...

【技术追踪】InverseSR:使用潜在扩散模型进行三维脑部 MRI 超分辨率重建(MICCAI-2023)
LDM 实现三维超分辨率~ 论文:InverseSR: 3D Brain MRI Super-Resolution Using a Latent Diffusion Model 代码:https://github.com/BioMedAI-UCSC/InverseSR 0、摘要 从研究级医疗机构获得的高分辨率(HR)MRI 扫描能够提供关于成像…...
-变量)
React学习(二)-变量
也是很无聊,竟然写这玩意,毕竟不是学术研究,普通工作没那么多概念性东西,会用就行╮(╯▽╰)╭ 在React中,变量是用于存储和管理数据的基本单位。根据其用途和生命周期,React中的变量可以分为以下几类: 1. 状态变量(State) 用途:用于存储组件的内部状态,状态变化会触…...

list重点接口及模拟实现
list功能介绍 c中list是使用双向链表实现的一个容器,这个容器可以实现。插入,删除等的操作。与vector相比,vector适合尾插和尾删(vector的实现是使用了动态数组的方式。在进行头删和头插的时候后面的数据会进行挪动,时…...
基础知识④)
【自然语言处理与大模型】大模型(LLM)基础知识④
(1)微调主要用来干什么? 微调目前最主要用在定制模型的自我认知和改变模型对话风格。模型能力的适配与强化只是辅助。 定制模型的自我认知:通过微调可以调整模型对自我身份、角色功能的重新认知,使其回答更加符合自定义…...
:分布式架构与微服务)
系统架构设计(九):分布式架构与微服务
基础定义 架构类型定义分布式架构指将系统部署在多个服务器节点上,通过网络协作完成整体功能。强调物理上的分布与任务协作。微服务架构一种分布式架构模式,将系统按照业务维度拆分为多个小型自治服务,每个服务可独立开发、部署、伸缩。 核…...

Java 框架配置自动化:告别冗长的 XML 与 YAML 文件
在 Java 开发领域,框架的使用极大地提升了开发效率和系统的稳定性。然而,传统框架配置中冗长的 XML 与 YAML 文件,却成为开发者的一大困扰。这些配置文件不仅书写繁琐,容易出现语法错误,而且在项目规模扩大时ÿ…...

vue使用Pinia实现不同页面共享token
文章目录 一、概述二、使用步骤安装pinia在vue应用实例中使用pinia在src/stores/token.js中定义store在组件中使用store登录成功后,将token保存pinia中向后端API发起请求时,携带从pinia中获取的token 三、参考资料 一、概述 Pinia是Vue的专属状态管理库…...

遨游科普:三防平板是什么?有什么功能?
清晨的露珠还挂在帐篷边缘,背包里的三防平板却已开机导航;工地的尘土飞扬中,工程师正通过它查看施工图纸;暴雨倾盆的救援现场,应急队员用它实时回传灾情数据……这些看似科幻的场景,正因三防平板的普及成为…...

spring MVC 至 springboot的发展流程,配置文件变化
spring mvc Spring MVC 是 Spring 框架中的一个重要模块,用于构建基于 Java 的 Web 应用程序。它基于 MVC(Model-View-Controller)设计模式,提供了灵活、可配置的方式来开发动态网页或 RESTful 服务 ssm SSM 框架…...

深入解析Spring Boot与JUnit 5的集成测试实践
深入解析Spring Boot与JUnit 5的集成测试实践 引言 在现代软件开发中,测试是确保代码质量和功能正确性的关键环节。Spring Boot作为目前最流行的Java Web框架之一,提供了强大的支持来简化测试流程。而JUnit 5作为最新的JUnit版本,引入了许多…...
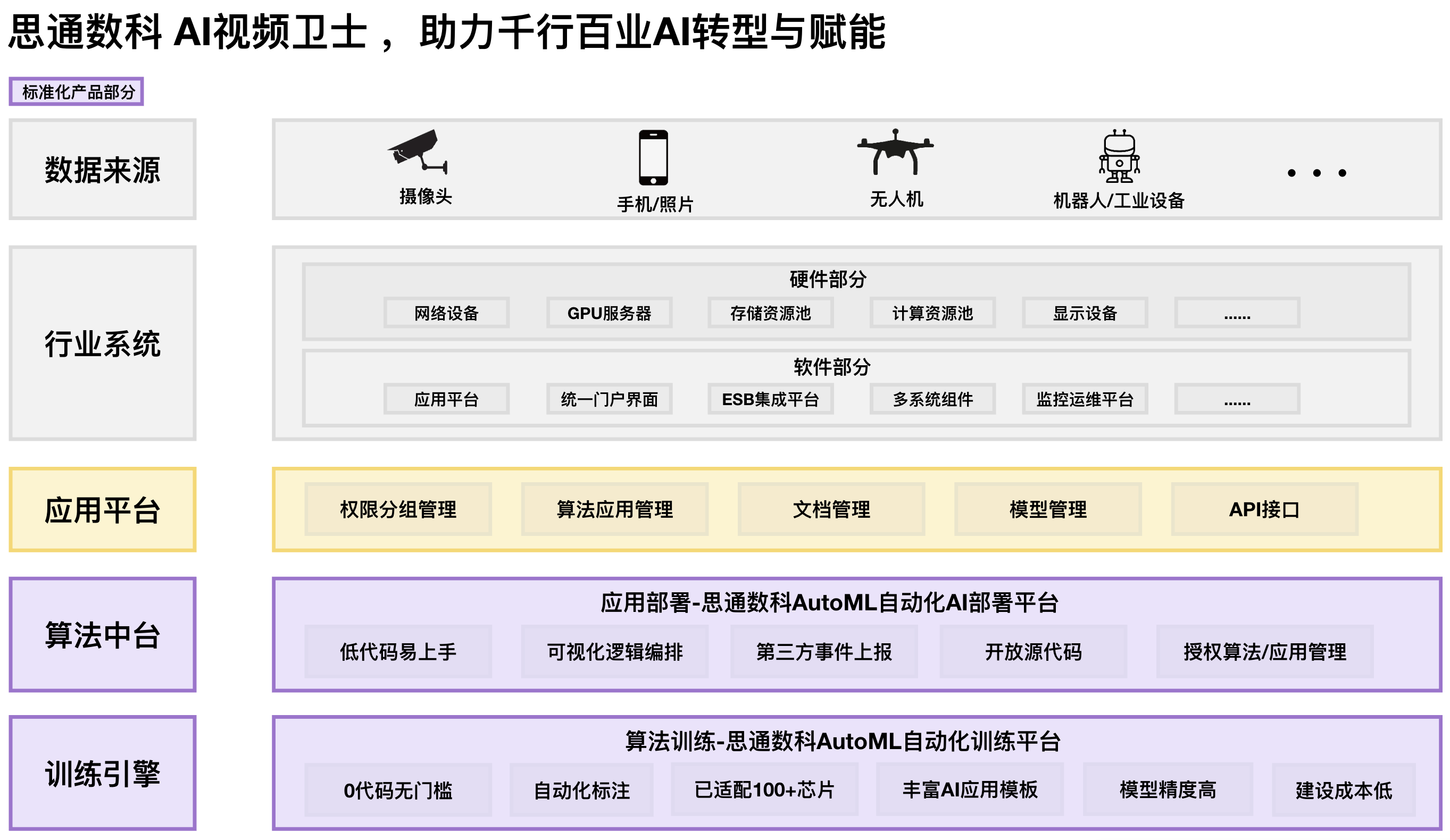
AI全域智能监控系统重构商业清洁管理范式——从被动响应到主动预防的监控效能革命
一、四维立体监控网络技术架构 1. 人员行为监控 - 融合人脸识别、骨骼追踪与RFID工牌技术,身份识别准确率99.97% - 支持15米超距夜间红外监控(精度0.01lux) 2. 作业过程监控 - UWB厘米级定位技术(误差<0.3米&…...
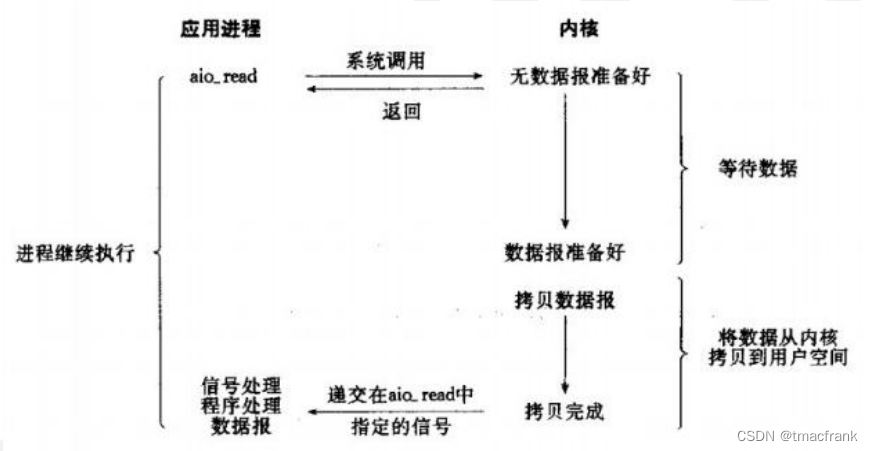
网络编程中的直接内存与零拷贝
本篇文章会介绍 JDK 与 Linux 网络编程中的直接内存与零拷贝的相关知识,最后还会介绍一下 Linux 系统与 JDK 对网络通信的实现。 1、直接内存 所有的网络通信和应用程序中(任何语言),每个 TCP Socket 的内核中都有一个发送缓冲区…...

区块链基本理解
文章目录 前言一、什么是分布式账本(DLT)二、什么是P2P网络?二、共识算法三、密码算法前言 区块链是由一个一个数据块组成的链条,按照时间顺序将数据块逐一链接,通过哈希指针链接,所有的数据块共同维护一份分布式账本(DLT),每个节点(可以理解为一个玩家,一台计算机)都拥…...

panda机械臂的正逆运动学分析与仿真
文章目录 前言Panda机械臂的DH参数法建模正运动学逆运动学误差函数雅可比矩阵高斯-牛顿法(Gauss-Newton) 参考代码获取 前言 机械臂的位置运动学分析是机器人控制与轨迹规划的核心基础,其研究内容主要分为正运动学(Forward Kinem…...

QT使用QXlsx读取excel表格中的图片
前言 读取excel表格中的图片的需求比较小众,QXlsx可以操作excel文档,进行图片读取、插入操作,本文主要分享单独提取图片和遍历表格提取文字和图片。 源码下载 github 开发环境准备 把下载的代码中的QXlsx目录,整个拷贝到所创建…...
VulnHub | Breach - 1
🌟 关注这个靶场的其它相关笔记:[网安靶场] 红队综合渗透靶场 —— VulnHub 靶场笔记合集 Breach: 1 ~ VulnHubBreach: 1, made by mrb3n. Download & walkthrough links are available.https://vulnhub.com/entry/breach-1,152/ 0x01:…...

CMake基础及操作笔记
CMake 基础与操作:从入门到精通 前言 CMake 是一个功能强大、跨平台的构建工具,广泛用于 C 项目管理。它通过简洁的配置文件(CMakeLists.txt)描述编译过程,生成适用于不同平台的构建脚本(如 Makefile 或 …...

在Oracle到GreatSQL迁移中排序规则改变引发的乱码问题分析及解决
在Oracle到GreatSQL迁移中排序规则改变引发的乱码问题分析及解决 一、引言 某老系统数据库从 Oracle 迁移至 GreatSQL 过程中,首批迁移(存储过程、表结构、基础数据)顺利完成。然而,第二批数据迁移时出现主键冲突问题࿱…...

开源物联网平台(OpenRemote)
在物联网技术蓬勃发展的当下,OpenRemote作为一款强大的开源物联网平台,正逐渐在多个领域崭露头角。尤其是在智能能源管理领域,它为微电网和分布式能源网络提供了全面且灵活的数据集成与管理方案,展现出独特的优势。 OpenRemote提供…...

JavaScript入门【3】面向对象
1.对象: 1.概述: 在js中除了5中基本类型之外,剩下得都是对象Object类型(引用类型),他们的顶级父类是Object;2.形式: 在js中,对象类型的格式为key-value形式,key表示属性,value表示属性的值3.创建对象的方式: 方式1:通过new关键字创建(不常用) let person new Object();// 添…...

软件安全检测报告:如何全面评估企业级办公软件安全性?
软件安全检测报告对软件的整体安全性进行了全面而细致的评估与呈现,既揭露了软件防范非法入侵的能力,同时也为软件的开发与优化提供了关键性的参考依据。 引言情况 撰写报告旨在明确呈现软件的安全性状态,并为后续的改进工作提供依据。在阐…...
)
区间dp(竞赛)
一、介绍 区间 dp 其实就是左右端点固定之后,用已经得出的小区间来更新大区间答案的 dp 方式。 非常重要的要素:小区间得到大区间,衍生出来的问题就是对于大区间如何划分成若干小区间,这直接决定了方程的书写。之后的例题中慢慢…...

PySide6 GUI 学习笔记——常用类及控件使用方法(常用类颜色常量QColorConstants)
文章目录 一、概述二、颜色常量表标准 Qt 颜色SVG 颜色(部分) 三、Python 代码示例四、代码说明五、版本兼容性六、延伸阅读 一、概述 QColorConstants 是 Qt for Python 提供的一个预定义颜色常量集合,包含标准Qt颜色和SVG规范颜色。这些常…...

大模型技术演进与应用场景深度解析
摘要 本文系统梳理了当前主流大模型的技术架构演进路径,通过对比分析GPT、BERT等典型模型的创新突破,揭示大模型在参数规模、训练范式、应用适配等方面的核心差异。结合医疗、金融、教育等八大行业的实践案例,深入探讨大模型落地的技术挑战与解决方案,为从业者提供体系化的…...
