当前位置：首页 > article >正文

机器学习 Day18 Support Vector Machine ——最优美的机器学习算法

article 2025/9/19 8:26:00

1.问题导入：

2.SVM定义和一些最优化理论

2.1SVM中的定义

2.1.1 定义

SVM 定义：SVM（Support Vector Machine，支持向量机）核心是寻找超平面将样本分成两类且间隔最大。它功能多样，可用于线性或非线性分类、回归、异常值检测等，在机器学习领域地位重要，尤其适合中小规模复杂数据集分类。
- 图中不同颜色点代表不同类别样本，超平面是分割两类样本的平面，位于超平面两侧且离超平面最近的样本点（绿圈标注）就是支持向量，它们决定超平面位置（之后数学推导会有说明），而超平面要使两类样本间隔最大。
2.1.2 超平面最大间隔
- 左图分析：展示三种线性分类器决策边界，虚线代表的模型无法正确分类，其余两个模型虽在训练集表现好，但决策边界离样本太近，新样本出现时泛化能力可能差（欠拟合）。
- 右图分析：SVM 分类器决策边界（实线），既分离了两个类别，又尽可能远离最近训练实例，这样能有更好泛化能力，降低过拟合风险。
2.1.3 硬间隔
- 概念：严格要求所有实例不在最大间隔之间且位于正确一边的分类方式。
- 问题：
  - 条件苛刻，仅在数据线性可分时有效，若数据线性不可分则找不到合适硬间隔。
  - 对异常值敏感，一个异常值就可能大幅改变决策边界，使其无法很好泛化。左图因异常值找不到硬间隔，右图有异常值时决策边界与无异常值时差异大。
2.1.4 软间隔
- 概念：为避免硬间隔分类问题，在保持最大间隔宽阔和限制间隔违例（位于最大间隔之上或错误一边的实例）间找平衡的分类方式。
- 参数 C 作用：在 Scikit - Learn 的 SVM 类中，超参数 C 控制平衡。C 值小，间隔宽，间隔违例多；C 值大，间隔窄，间隔违例少（数学推导中说明）。左图 C = 100，错误样本少但间隔小；右图 C = 1，间隔大，多数间隔违例在决策边界正确一边，泛化效果可能更好。

2.2最优化理论

2.2.1对偶理论

注意原问题的对偶问题中是先对拉格朗日函数求w的下确界，再对构造的参数因子求最大。
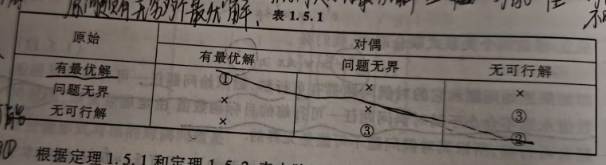
问题3就是弱对偶理论，问题5就是强对偶理论，以上图片中仅仅涉及到SVM需要的理论，这里对于感兴趣的读者，可以观看以下关于对偶理论的补充（不做证明）

1.如果一个原始LP问题存在最优解，那么它的对偶问题也存在最优解，并且最优值相等

2.由1推出：若x和w分别是原始问题，以及其对偶问题的可行解，则x和w分别是原问题的最优解充要条件是它们对应的优化函数值相等

3.给定一个原始LP问题和对偶问题，它们的解的情况有且仅有以下表格中的一种情况出现：

2.2.2凸优化理论

2.2.2.1凸函数

2.2.2.2凸优化

所以说，如果一个优化问题我们可以转换为凸优化问题，那么会很简单，常见也有很多求解凸优化的问题，针对无约束的和带有约束的。

2.2.2.3直线距离公式

3.SVM算法推导

我们只说SVM用于分类的推导，并且只说用于二分类的推导，多分类会由二分类得到

数据在空间中常常被分为3类：线性可分，近似线性可分，线性不可分，在SVM中分别对应的就是硬间隔，软间隔，核技巧，文章会一一解释：

3.1线性可分模型——硬间隔处理

最直观的想法就是我们可以直接通过一条线对这个线性可分的模型进行处理，比如说就是这条直线（二维是直线，高维就是超平面了），直线方程可以是图中方程，然后我们给一个预测样本，我们就去带入这个超平面，如果这个在上方就是正类，下方就是负类，所以模型就是这样：

我们承认的是一般情况下如果存在一条直线可以把两个类分开，那么就存在无数条直线把这两个类分开，那么我们如何衡量那条直线效果最好呢。我们SVM的衡量方法就是把这条直线向上向下平移直到与某个或者某几个样本点相交，这时我们去选择一个间隔最大的直线即可，比如这个图

但仅仅这样就可以确定一条直线的位置吗，显然不行，因为在这个间隔之间的任何一条直线显然都可以通过平移得到这个最大间隔，所以为了保证唯一，我们选取的直线位于这条间隔之间，现在我们就可以建立优化模型了：

对于一个输入：，注意这里不限制维数，即x是一个多维度的向量，y是一个标签，用来表示类别，当然你可以不是正负一，但是这里正负一方便以后的计算，我们做出以下规定：显然这个最大间距就是由先接触的点决定的，这些点我们叫做支持向量，我们计算支持向量x0到这条直线的距离乘以2即可，观察距离公式，显然可以通过相等比例放缩w和b得到的是同一个直线，所以我们可以通过放缩来使得分母部分为1，即|w^Tx0+b|=1，此时支持向量到超平面的距离为||w||^-1，所以有如下最优化方程：

注意这个优化问题是凸优化，你别看约束域有点复杂，但其实我们基变量是w和b，yi是已知的，所以约束函数就是一次的，而且最优化函数二次的，所以这是一个凸二次规划问题！求解凸优化有很多算法，之后用其求解即可，当然我们还可以做进一步的简化，这里先不讲，因为我们之后两个模型和这个模型的简化方法一样，之后建完模型后会统一讲解。

3.2近似线性可分模型——软间隔处理

对于线性可分模型的建模，可以肯定的是一点会解出一个（w，b），但是对于近似线性可分模型，如果仍然使用以上模型，会有约束条件矛盾的情况，即不存在（w，b）来使得模型成立，这时候我们只需要引入松弛变量即可，（松弛变量的目的就是在于使得约束条件不是那么的严格成立，对应于SVM就是我们容忍一些点存在于间隔之间），所以约束条件就变成了：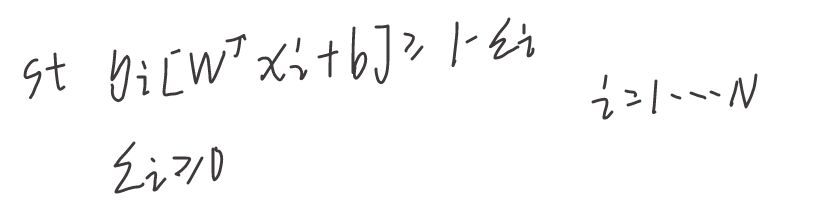

但是显然如果松弛变量取得很大，上面那个1- $epsl$ 是负数，很明显恒成立，所以我们要给目标函数加上一个罚函数的限制（正则项）：注意这里C是事先设定的一个值，C就是我们在2.1.4中介绍的C。C越大，惩罚力度越大，为了使目标函数小， $epsl$ 就得少一点，所以对应的就是违反原不等式的少，对应图，就是违反点少，就是间隔违例少。

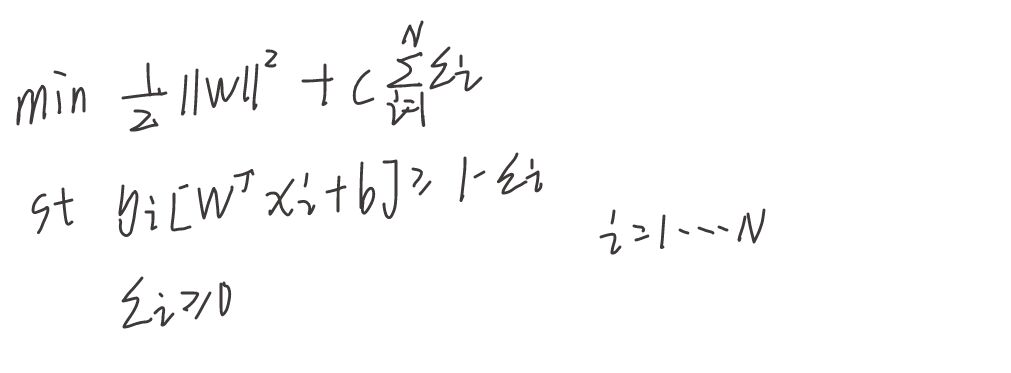
以上就是对于近似线性可分的处理，当然这个需要优化的变成了（w，b， $epsl$ ），当然还是一个凸二次规划，也可以使用一些算法（SMO），简化这个问题还和上边一样，我们在最后一节会讲到。显然这个模型可以包含第一个模型，在这个模型里另 $epsl$ 全部为0即可。所以我们以后在高维也是推广此类模型。

3.3线性不可分模型——核技巧

3.3.1核函数

低维不可分数据在高维中有很大概率变为线性可分，SVM并没有像其他算法一样去改变形状，比如决策树算法等就是通过一些折线啥的去处理这种情况，但SVM是讲数据投射到高维度进行处理，当然核技巧并不是SVM所特有的，之所以我们说SVM很优美，之后我们会看到（利用核函数避免了维度计算带来的灾难），核技巧如何用于模型求解，现在我们先讲核函数

一般的规律是维度越高，变成线性可分的概率就会越大，所以我们希望映射函数是一个到无穷维空间的映射，面临的问题就是我们如何计算这个向量的值，因为它是一个无穷维的，但是我们一会回看到不需要计算这个值，可以通过K来完成整个算法。那么什么样的函数可以作为一个核函数呢，在泛函分析中有如下定理：

核函数一般情况下有如下：

一般情况下经常使用RBF核。

3.3.2 原理推导

模型和3.2大致相同，和3.2不同的是仅仅把x的位置改为映射函数即可，且此时对应的w也要对应相应的维度。所以模型是：

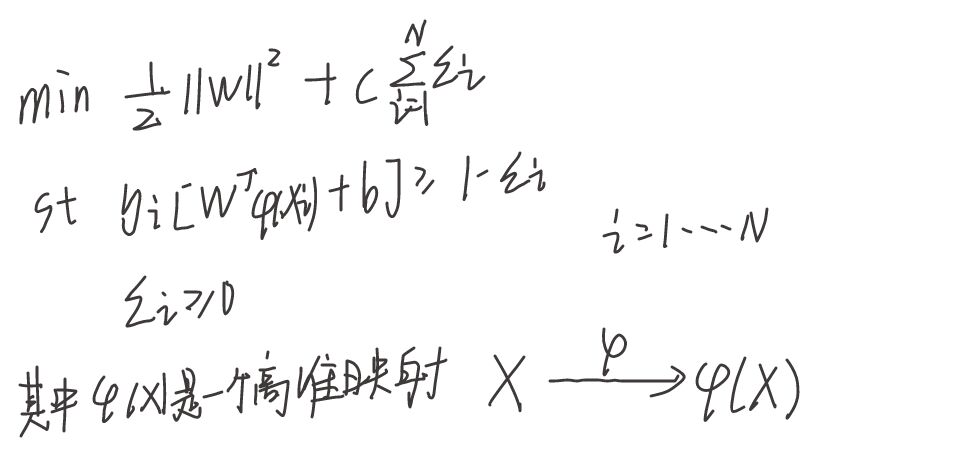
接下来我们来尝试简化模型，注意模型3.1和3.2的求解一样。

我们注意这个优化所有的条件满足 2.2.1中的强对偶性，即它的对偶问题最优值和它一样，所以我们转变为求他的对偶问题，注意该模型是没有等式条件的。其对偶问题是：

我们先来看L的极值，直接求导即可：

可以看到我们在未知映射的条件下利用核函数求得了算法，避免了高维计算。这是一大亮点。

这个优化函数中我们可以发现只有带求参数是未知的而且另一个参数没有了，所以优化模型变为：

我们求解这个凸优化问题会得到最优值，接下来利用这些求（w，b）即可：求w的时候有以上公式，但这里我们是不知道映射的，那怎么办呢？其实我们不需要知道这个映射，这又是SVM的一个亮点：

我们并不需要计算w就可以得到结果，求b的话需要用到KKT条件：

至此给定一个样本就可以按照以上公式判别他的类别，注意观察上面的公式，涉及到对 $\alpha$ 的求和，所以这个解当 $\alpha$ 为0时，不影响算法，影响算法的仅仅是 $\alpha$ 不为0，而由互补松弛条件，对应的，注意还有 $\varepsilon$ =0，这就是支持向量的所在超平面，所以这就是我们开头说的，只有支撑向量会影响算法！！算法流程是：