【蓝桥杯真题精讲】第 16 届 Python A 组(省赛)
文章目录
- T1 偏蓝 (5'/5')
- T2 IPv6 (0'/5')
- T3 2025 图形 (10'/10')
- T4 最大数字 (10'/10')
- T5 倒水 (15'/15')
- T6 拼好数 (0'/15')
- T7 登山 (20'/20')
- T8 原料采购 (20'/20')
更好的阅读体验
- 高速访问:https://wiki.dwj601.cn/ds-and-algo/lan-qiao-cup/16th-python-a/
- 永久链接:https://explorer-dong.github.io/ds-and-algo/lan-qiao-cup/16th-python-a/
官方还没有开放评测,洛谷 开放了全部评测,但是时间限制与比赛不太一样,往往更加严格,所以可能会出现洛谷过不了,但其实赛时能过的情况。
T1 偏蓝 (5’/5’)
题意:定义三元组中每一位的取值范围为 [ 0 , 255 ] [0,255] [0,255] 的整数,问有多少个三元组满足:三元组中的第三个位置的数严格大于前两个位置的数。
思路:直接三重循环遍历一遍即可。
最终答案为: 5559680 5559680 5559680
ans = 0
for i in range(256):for j in range(256):for k in range(256):ans += (k > i) and (k > j)
print(ans)
T2 IPv6 (0’/5’)
题意:问所有的最简 IPv6 的表示形式有多少种。
思路:不会,TODO。
T3 2025 图形 (10’/10’)
题意:给定 h , w ( 1 ≤ h , w ≤ 100 ) h,w\ (1\le h,w\le 100) h,w (1≤h,w≤100),按照 2 , 0 , 2 , 5 2,0,2,5 2,0,2,5 的顺序循环打印一个 h h h 行 w w w 列的字符串矩阵,同行中没有空格。
思路:纯模拟。
时间复杂度: O ( h w ) O(hw) O(hw)
h, w = tuple(map(int, input().strip().split()))a = ['2', '0', '2', '5']for i in range(h):ans = ''idx = i % 4j = 0for j in range(w):ans += a[idx]idx = (idx + 1) % 4print(ans)
T4 最大数字 (10’/10’)
题意:给定一个含有 n ( 1 ≤ n ≤ 10 4 ) n\ (1\le n\le 10^4) n (1≤n≤104) 个数的排列,现在需要重排使得重排后的序列中所有元素「二进制拼接」后的二进制数值最大,输出这个最大二进制数对应的十进制数。
思路:
- 贪心题,就是自定义一个排序规则。对于 x x x 和 y y y 两个二进制表示,如果 x + y > y + x x+y>y+x x+y>y+x,则 x x x 要排在 y y y 的前面(加号表示字符串拼接);
- Python 对字符串与十进制数的转换有限制,需要手动调大。每个数的二进制最多 14 14 14 位, n n n 个数开到 150000 150000 150000 肯定可以,但这是 Python 3.11 引入的,不知道蓝桥杯的评测机能不能过;
- 力扣原题,证明。
时间复杂度: O ( n log n ) O(n\log n) O(nlogn)
from functools import cmp_to_key
import sys
sys.set_int_max_str_digits(150000)def cmp(x: str, y: str) -> int:if x + y > y + x:return -1 # 小于号elif x + y == y + x:return 0return 1n = int(input().strip())a = [bin(x)[2:] for x in range(1, n + 1)]
a.sort(key=cmp_to_key(cmp))print(int(''.join(a), 2))
T5 倒水 (15’/15’)
题意:给定一个含有 n ( 1 ≤ n ≤ 10 5 ) n\ (1\le n\le 10^5) n (1≤n≤105) 个数的序列 a ( 1 ≤ a i ≤ 10 5 ) a\ (1\le a_i \le 10^5) a (1≤ai≤105) 和一个整数 k ( 1 ≤ k ≤ n ) k\ (1\le k\le n) k (1≤k≤n)。现在定义一种数值转移规则:对于第 i i i 个元素 a i a_i ai,其可以从任意一个 j < i j < i j<i 且 i ≡ j ( m o d k ) i\equiv j \pmod k i≡j(modk) 的元素中转移一部分数值到自己身上。问经过任意次这种转移操作后,序列最小的元素最大可以是多少。
思路:看到最大化最小元素立刻想到了二分,但是看到只能从前缀部分转移,扫描一遍就可以了。我们分 k k k 组,每组从左往右遍历并记录前缀元素数量、前缀和、前缀最小值:
- 如果当前元素比不小于前缀最小值,那么就不会影响全局最小值,不用操作;
- 如果当前元素严格小于前缀最小值,那么就肯定要拿前缀的数值转移一部分到自己身上,至于转移多少不重要,重要的是要更新转移后的前缀最小值。
时间复杂度: O ( n ) O(n) O(n)
n, k = tuple(map(int, input().strip().split()))
a = list(map(int, input().strip().split()))ans = max(a)
for i in range(k):cnt = 1pre = a[i]pre_min = a[i]for j in range(i + k, n, k):if a[j] >= pre_min:cnt += 1pre += a[j]continuecnt += 1pre += a[j]if pre // cnt >= pre_min:continuepre_min = pre // cntans = min(ans, pre_min)print(ans)
T6 拼好数 (0’/15’)
题意:给定一个含有 n ( 1 ≤ n ≤ 10 3 ) n\ (1\le n\le 10^3) n (1≤n≤103) 个数的序列 a ( 0 ≤ a i ≤ 10 9 ) a\ (0\le a_i \le 10^9) a (0≤ai≤109)。为了最大化「数字中 6 6 6 的个数超过 6 6 6 个」的数字个数,现在可以给这些数分组(每组不超过 3 个元素)并将同一个组的数直接拼起来。问「数字中 6 6 6 的个数超过 6 6 6 个」的数字个数最大是多少。
思路:不会,TODO。
T7 登山 (20’/20’)
题意:给定一个 n n n 行 m m m 列的矩阵 a ( 1 ≤ a i j ≤ 10 9 ) a\ (1\le a_{ij}\le 10^9) a (1≤aij≤109),满足 1 ≤ n , m ≤ 10 4 , 1 ≤ n × m ≤ 10 6 1\le n,m \le 10^4,1\le n\times m \le10^6 1≤n,m≤104,1≤n×m≤106。给定在矩阵中的行走规则:可以走到同行同列中任意一个满足「向左或向上比当前元素大的位置上」、「向右或向下比当前元素小的位置上」。计算每个格子可以到达的最大高度,输出其均值并保留 6 6 6 位小数。
思路:直接遍历每一个连通分量即可,可以用 DSU,也可以二次遍历来给连通分量中每个位置标上可到达的最大值。其余实现可以参考 01 迷宫 这道题。
时间复杂度: O ( n m ( n + m ) ) O(nm(n+m)) O(nm(n+m))
=== “Python BFS”
from collections import dequen, m = tuple(map(int, input().strip().split()))
g = [list(map(int, input().strip().split())) for _ in range(n)]
ans = [[0] * m for _ in range(n)]vis = [[False] * m for _ in range(n)]def bfs(u: int, v: int):q = deque()path = []ma = -1vis[u][v] = Truepath.append((u, v))q.append((u, v))ma = max(ma, g[u][v])while q:x, y = q.popleft()for j in range(m):if j < y and g[x][j] > g[x][y] and not vis[x][j]:vis[x][j] = Truepath.append((x, j))q.append((x, j))ma = max(ma, g[x][j])if j > y and g[x][j] < g[x][y] and not vis[x][j]:vis[x][j] = Truepath.append((x, j))q.append((x, j))ma = max(ma, g[x][j])for i in range(n):if i < x and g[i][y] > g[x][y] and not vis[i][y]:vis[i][y] = Truepath.append((i, y))q.append((i, y))ma = max(ma, g[i][y])if i > x and g[i][y] < g[x][y] and not vis[i][y]:vis[i][y] = Truepath.append((i, y))q.append((i, y))ma = max(ma, g[i][y])for x, y in path:ans[x][y] = mafor i in range(n):for j in range(m):if vis[i][j]:continuebfs(i, j)s = 0
for i in range(n):for j in range(m):s += ans[i][j]print(f"{s/(n * m):.6f}")
T8 原料采购 (20’/20’)
题意:在一维坐标轴正方向上,给定一辆位于原点处的货车,其容量为 m ( 1 ≤ m ≤ 10 9 ) m\ (1\le m\le 10^9) m (1≤m≤109)。正方向上有从近到远的 n ( 1 ≤ n ≤ 10 5 ) n\ (1\le n \le 10^5) n (1≤n≤105) 个进货源,每个进货源都有一个进货单价、存货量和到原点的距离,分别记作 a , b , c ( 1 ≤ a i , b i , c i ≤ 10 9 ) a,b,c\ (1\le a_i,b_i,c_i \le 10^9) a,b,c (1≤ai,bi,ci≤109)。货车每行驶 1 1 1 个单位花费 o o o 且无需返程。输出进满货的最低成本,若没有方案可以装满输出 − 1 -1 −1。
思路:一道比较经典的反悔贪心题,模拟的过程略复杂,但整体难度不大。初始贪心时直接选择即可;后续反悔时,每次和之前单价更高的货物进行置换。可以使用大根堆来维护选择过的「货物单价与货物数量」。至于路费,无需在货物置换的过程中考虑,只需在全部置换结束后再算上即可。
时间复杂度: O ( n log n ) O(n\log n) O(nlogn)
=== “Python”
from heapq import *MII = lambda: map(int, input().strip().split())class Site:def __init__(self, price, num, dist):self.price = priceself.num = numself.dist = distn, m, o = MII()
sites = [Site(*MII()) for _ in range(n)]def solve() -> None:# 特判if sum([site.num for site in sites]) < m:print(-1)return# 贪心val = 0 # 车上货物价值num = 0 # 车上货物数量i = 0 # 枚举到的进货点下标h = [] # [[货物单价的负数,选择的数量], [], ...]while i < n:choose = min(sites[i].num, m - num)if choose == 0:i -= 1breaksites[i].num -= choosenum += chooseval += choose * sites[i].priceheappush(h, [-sites[i].price, choose])i += 1# 反悔heapify(h)ans = val + sites[i].dist * owhile i < n:if sites[i].price >= -h[0][0]:i += 1continuealter_num = 0 # 第 i 个进货源替换货物的数量while len(h):if -h[0][0] <= sites[i].price:breakalter = min(h[0][1], sites[i].num) # 替换量h[0][1] -= altersites[i].num -= alteralter_num += alterval -= alter * (-h[0][0] - sites[i].price)if h[0][1] == 0:heappop(h)if sites[i].num == 0:breakif alter_num:heappush(h, [-sites[i].price, alter_num])ans = min(ans, val + sites[i].dist * o)i += 1print(ans)if __name__ == "__main__":solve()
=== “C++”
#include <iostream>
#include <queue>
using namespace std;
using ll = long long;const int N = 100010;ll n, m, o;
struct Site {ll price, num, dist;
} sites[N];int main() {ios::sync_with_stdio(false);cin.tie(nullptr);ll all_num = 0;cin >> n >> m >> o;for (int i = 0; i < n; i++) {cin >> sites[i].price >> sites[i].num >> sites[i].dist;all_num += sites[i].num;}// 特判if (all_num < m) {cout << -1 << "\n";return 0;}// 贪心ll val = 0, num = 0, i = 0;priority_queue<pair<ll, ll>> h;while (i < n) {ll choose = min(sites[i].num, m - num);if (!choose) {i--;break;}num += choose;sites[i].num -= choose;val += choose * sites[i].price;h.push({sites[i].price, choose});i++;}// 反悔ll ans = val + sites[i].dist * o;while (i < n) {if (h.top().first <= sites[i].price) {i++;continue;}ll alter_num = 0;while (h.size()) {if (h.top().first <= sites[i].price) {break;}auto [price, num] = h.top();h.pop();ll alter = min(num, sites[i].num);num -= alter;sites[i].num -= alter;alter_num += alter;val -= alter * (price - sites[i].price);if (num) {h.push({price, num});}if (!sites[i].num) {break;}}if (alter_num) {h.push({sites[i].price, alter_num});ans = min(ans, val + sites[i].dist * o);}i++;}cout << ans << "\n";return 0;
}
相关文章:
)
【蓝桥杯真题精讲】第 16 届 Python A 组(省赛)
文章目录 T1 偏蓝 (5/5)T2 IPv6 (0/5)T3 2025 图形 (10/10)T4 最大数字 (10/10)T5 倒水 (15/15)T6 拼好数 (0/15)T7 登山 (20/20)T8 原料采购 (20/20) 更好的阅读体验 高速访问:https://wiki.dwj601.cn/ds-and-algo/lan-qiao-cup/16th-python-a/永久链接࿱…...

Java接口设计:ECharts热力图的绘制
引言 热力图是一种强大的数据可视化工具,通过颜色的深浅变化来直观展示数据密度和分布情况。在现代Web应用中,ECharts作为一款流行的开源数据可视化库,提供了丰富的图表类型,其中热力图因其直观的视觉效果而被广泛使用。本教程将…...

深入理解 MongoDB 的 _id 和 ObjectId:从原理到实践
在 MongoDB 的世界中,_id 字段和 ObjectId 是每个开发者都必须理解的核心概念。作为 MongoDB 文档的唯一标识符,它们不仅影响着数据库的设计,也直接关系到应用的性能和扩展性。本文将全面剖析 _id 和 ObjectId 的工作原理、实际应用场景以及最…...

C++内存复制
C内存复制 方法1 g_savedPoints.resize(pResult->contourData.contourPointCount);//方法1std::copy(pResult->contourData.pointArray, pResult->contourData.pointArray pResult->contourData.contourPointCount, g_savedPoints.begin());方法2 g_savedPoints.r…...

【notepad++如何设置成中文界面呢?】
“Notepad”是一款非常强大的文本编辑软件,将其界面设置成中文的方法如下: 一、工具/原料: 华为 Matebook 15、Windows 10、Notepad 8.4.6。 二 、具体步骤: 1、找到任意一个文本文件,比如 txt 格式的文…...

当AI遇上科研:北大“科学导航”重塑学术探索全流程
在人工智能技术迅猛发展的当下,一场悄然发生的变革,正在改变我们“做科研”的方式。近日,北京大学科学智能研究院联合深势科技,正式上线一款面向科研人员的一体化AI平台——Science Navigator(科学导航)。这…...

大模型在闭合性胫骨平台骨折诊疗全流程中的应用研究报告
目录 一、引言 1.1 研究背景与目的 1.2 国内外研究现状 1.3 研究方法与创新点 二、大模型预测原理及数据基础 2.1 大模型概述 2.2 数据收集与处理 2.3 模型训练与优化 三、术前预测与方案制定 3.1 骨折类型及损伤程度预测 3.2 手术时机评估 3.3 手术方案制定 3.4 …...

PHP学习笔记(八)
目录 返回值 return的使用 多值返回的替代方案 可变函数 内部(内置)函数 匿名函数 静态匿名函数 返回值 值通过可选参数的返回语句返回 return的使用 函数不能返回多个值,但可以通过返回一个数组来得到类似的效果 函数返回一个引用&am…...

C#中WSDL文件引用问题
工作中碰到一个单点登录的需求,因为这个需求同事别的系统已经做过,我这边只需要把代码迁移过来即可,但是迁移过程中发现引用WSDL文件后,方法报错的问题,各种排查代码之后未解决,最终发现是WSDL文件引用的问…...

Ubuntu 22.04上升级Node.js版本
在Ubuntu 22.04上升级Node.js版本有几种方法,推荐使用NVM(Node Version Manager),因为它可以让你轻松管理多个Node.js版本。 方法1: 使用NVM(推荐) 1. 安装NVM # 下载并安装NVM curl -o- https://raw.gi…...

养生新策:五维开启健康生活
一、饮食:天然食材,科学配比 以 “原型食物” 为主,减少加工食品摄入。早餐用鹰嘴豆泥涂抹全麦面包,搭配水煮蛋和一小把蓝莓,兼顾蛋白质与抗氧化物质;午餐选择藜麦饭,配上香煎鸡胸肉和蒜蓉空心…...
原理)
生成对抗网络(GAN)原理
生成对抗网络(GAN)原理 介绍示例代码一、GAN 的基本结构1. 生成器(Generator,记作 G)2. 判别器(Discriminator,记作 D) 二、对抗过程(博弈思想)三、训练过程四…...

【SpringBoot实战指南】使用 Spring Cache
文章目录 一、Spring Cache简介核心特点: 二、基础配置1. 添加依赖2. 启用缓存3. 缓存配置方案方案1:通过 yml 配置文件方案2:自定义 Bean 三、 缓存注解使用示例1.Cacheable - 数据查询缓存2.CachePut - 更新数据并缓存3.CacheEvict - 删除缓…...

centos8 配置网桥,并禁止kvm默认网桥
环境背景: 我使用vmware部署了一台kvm服务器,网络模式是nat。我想要kvm创建的虚拟机可以访问公网;所以kvm默认的地址不行,我必须使用nat地址才可以; 实现方式: 创建一个网桥,将本地的网络接口…...

C++:list容器,deque容器
list容器:双向链表容器,底层是双向链表。 简单使用如下: #include<iostream> #include<list> using namespace std;int main() {list<int> lst;lst.push_back(1);lst.push_back(2);lst.push_back(3);lst.push_front(4);l…...

【Node.js】全栈开发实践
个人主页:Guiat 归属专栏:node.js 文章目录 1. Node.js 全栈开发概述1.1 全栈开发的优势1.2 Node.js 全栈开发技术栈 2. 开发环境搭建2.1 Node.js 和 npm 安装2.2 开发工具安装2.3 版本控制设置2.4 项目初始化流程 3. 后端开发 (Node.js)3.1 Express 框架…...

自定义类型-联合体
概念 联合体是一种特殊的数据类型,允许在相同的内存位置存储不同的数据类型 联合体的所有成员共享同一块内存空间,大小由最大的成员决定 用于在同一块内存单元内存放不同类型的变量 语法结构 结构与结构体类似, union 共用体名 {成员列…...

Qt项目开发中所遇
讲述下面代码所表示的含义: QWidget widget_19 new QWidget(); QVBoxLayout *touchAreaLayout new QVBoxLayout(widget_19);QWidget *buttonArea new QWidget(widget_19); 1、新建一个名为widget_19的QWidget,将给其应用垂直管路布局。 2、新建一个…...

ubuntu sh安装包的安装方式
ubuntu sh安装包的安装方式以Miniconda2为例 https://repo.anaconda.com/miniconda/ 如果需要python2.7版本可下载以下版本 Miniconda2-latest-Linux-x86_64.sh 打开终端输入安装命令 sudo sh Miniconda2-latest-Linux-x86_64.sh 然后按提示安装,注意安装位置 …...

Redis语法大全
一、String(字符串) 特点:单键值存储,值可为字符串、数字,支持原子操作。 常用命令 SET 语法:SET key value [EX seconds] [PX milliseconds] [NX|XX]说明:设置键值对,可指定过期时…...

OpenAI宣布:核心API支持MCP,助力智能体开发
今天凌晨,OpenAI全资收购io的消息成为头条。同时,OpenAI还宣布其核心API——Responses API支持MCP服务。过去,开发智能体需通过函数调用与外部服务交互,过程复杂且延迟高。而今,Responses API支持MCP后,开发…...

我的爬虫夜未眠:一场与IP限流的攻防战
深夜的办公室里,键盘声此起彼伏,屏幕的蓝光映在程序员的脸上。我揉了揉酸胀的眼睛,第8次刷新日志页面——依旧是刺眼的“429 Too Many Requests”(请求过多)。这是本月第三次因为IP被目标网站封禁而被迫中断爬虫任务了…...

git:The following paths are ignored by one of your
遇到错误: The following paths are ignored by one of your .gitignore files: www hint: Use -f if you really want to add them. 说明:Git 拒绝添加 www/html/index.php,因为你的 .gitignore 中忽略了整个 www/ 目录(即 ww…...

算法--js--组合总和
题:给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。candidates 中的 同一个 数字可以 无限制重复…...
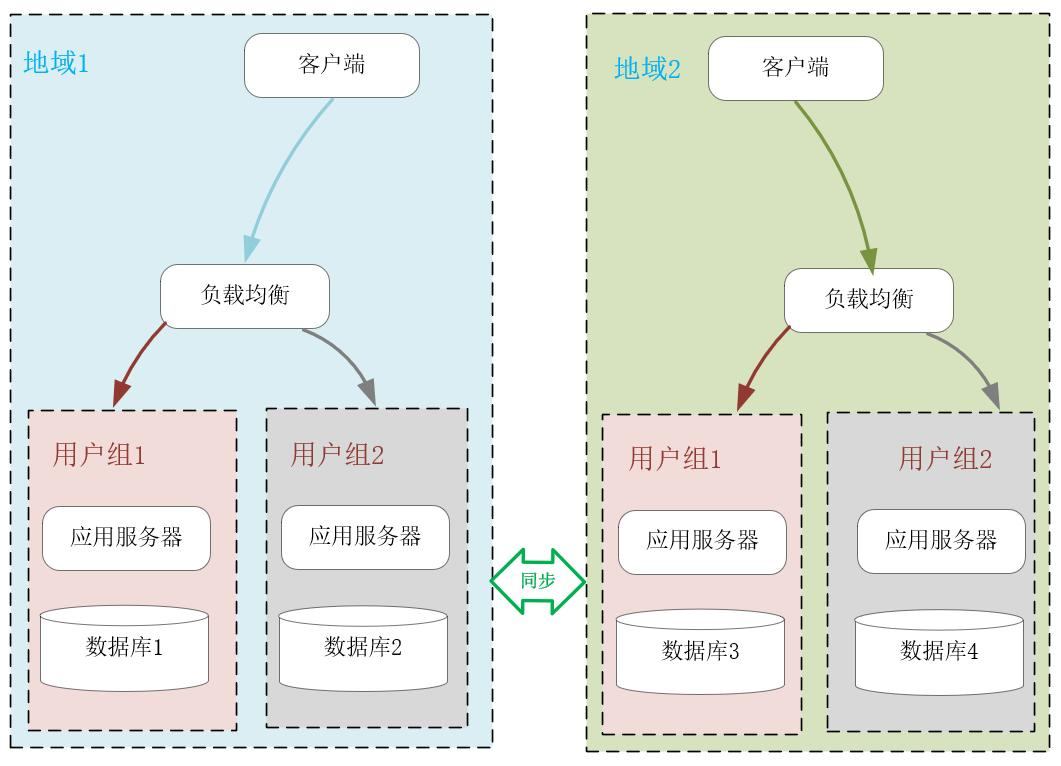
微服务中的 AKF 拆分原则:构建可扩展系统的核心方法论
在数字化浪潮的推动下,互联网应用规模呈指数级增长,传统单体架构逐渐暴露出难以扩展、维护成本高等问题,微服务架构应运而生并成为企业应对复杂业务场景的主流选择。然而,随着业务的不断扩张和用户量的持续增加,如何确…...

vue element-plus 集成多语言
main.js中 // 引入i18n import i18n from /i18n/index 使用i18 app.use(i18n) 在App.vue中 <template><el-config-provider :locale"locale" namespace"el" size"small"><router-view /></el-config-provider> </tem…...
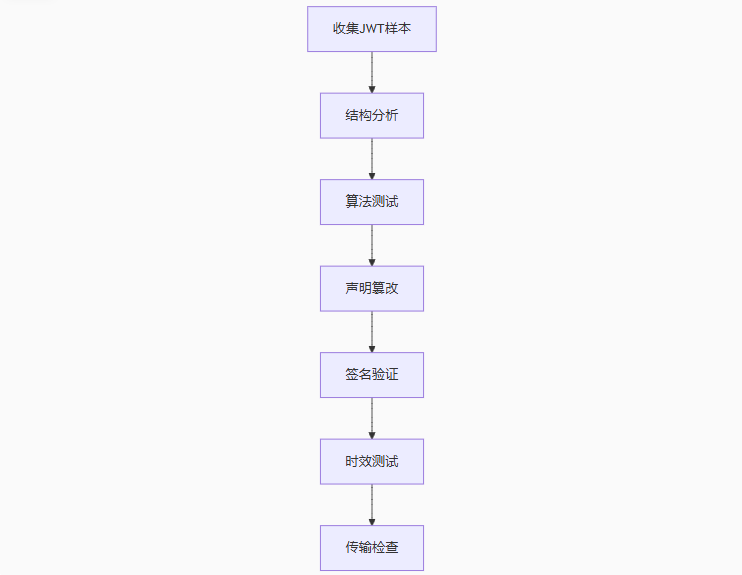
如何测试JWT的安全性:全面防御JSON Web Token的安全漏洞
在当今的Web应用安全领域,JSON Web Token(JWT)已成为身份认证的主流方案,但OWASP统计显示,错误配置的JWT导致的安全事件占比高达42%。本文将系统性地介绍JWT安全测试的方法论,通过真实案例剖析典型漏洞,帮助我们构建全…...

车载网关策略 --- 车载网关重置前的请求转发机制
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 钝感力的“钝”,不是木讷、迟钝,而是直面困境的韧劲和耐力,是面对外界噪音的通透淡然。 生活中有两种人,一种人格外在意别人的眼光;另一种人无论…...

EtpBot:安卓自动化脚本开发神器
EtpBot 是什么? EtpBot是一款专为安卓设备设计的自动化脚本开发工具,支持用户通过编写脚本实现自动化操作。该模块提供了丰富的API接口,涵盖点击、滑动、输入、截图等常见操作,帮助开发者快速构建自动化任务。ETPBot支持多设备并行…...

连锁企业管理系统对门店运营的促进作用
连锁企业管理系统通过整合数字化工具与流程优化,能从多维度提升门店运营效率与竞争力,以下是其对门店运营的具体促进作用: 一、数据化管理:精准决策与运营监控 实时数据同步与分析 系统可整合各门店销售数据、库存信息、客流统计…...
