【洛谷 P9025】 [CCC2021 S3] Lunch Concert 题解
题目: 洛谷 P9025
分析: 为了解决这个问题,我们需要找到一个整数位置 c 来举办音乐会,使得所有人移动到能听到音乐会的位置的时间总和最小。每个人移动后的位置应该在其听力范围内,并且尽可能靠近自己的初始位置以减少移动距离。
方法思路
-
问题分析:
- 每个人的听力范围是
[c - D_i, c + D_i],其中D_i是第i个人的听力距离。 - 如果初始位置
P_i在听力范围内,移动距离为0。 - 如果
P_i在听力范围左侧,需要移动到c - D_i,移动距离为(c - D_i) - P_i。 - 如果
P_i在听力范围右侧,需要移动到c + D_i,移动距离为P_i - (c + D_i)。
- 每个人的听力范围是
-
关键观察:
- 总移动时间是关于
c的分段线性函数,具有最小值点。 - 最小值点出现在总斜率由负变正的区间内,此时总移动时间最小。
- 总移动时间是关于
-
算法选择:
- 收集所有关键点(听力范围的左右边界),并排序。
- 计算每个区间的总斜率,找到总斜率由负变正的区间,该区间内的所有
c对应的总移动时间相同且最小。
解决代码
#include <bits/stdc++.h> // 包含所有标准库头文件
using namespace std;
using ll = long long; // 长整型别名,处理大整数(题目提示答案可能超过2^32)// 事件结构体:记录听力范围边界点及对总斜率的影响
struct Event {ll x; // 事件点位置(听力范围的左/右边界)ll delta; // 该事件点引起的总斜率变化量(+W[i])Event(ll x, ll delta) : x(x), delta(delta) {} // 构造函数// 按事件点位置排序(用于后续处理区间)bool operator<(const Event& other) const {return x < other.x;}
};int main() {ios::sync_with_stdio(false); // 加速输入输出cin.tie(nullptr);int N;cin >> N; // 读取人数vector<ll> P(N), W(N), D(N); // 存储每个人的初始位置、速度、听力距离vector<Event> events; // 存储所有事件点(听力范围边界)ll sum_W = 0; // 所有人的速度之和(用于计算初始斜率)// 读取每个人的信息,并生成事件点for (int i = 0; i < N; ++i) {cin >> P[i] >> W[i] >> D[i];sum_W += W[i]; // 累加速度总和// 每个人的听力范围是 [c-D[i], c+D[i]](c是音乐会位置)// 但我们需要分析当c变化时,每个人的移动时间如何变化// 关键观察:当c跨过 P[i]-D[i] 或 P[i]+D[i] 时,移动时间的斜率会变化ll A = P[i] - D[i]; // 听力范围左边界(当c < A时,此人需要右移)ll B = P[i] + D[i]; // 听力范围右边界(当c > B时,此人需要左移)// 事件点:当c经过A或B时,总斜率会变化// 每个事件点对应一个“斜率变化”:遇到左边界A时,斜率增加W[i];遇到右边界B时,斜率也增加W[i]events.emplace_back(A, W[i]); // 左边界事件events.emplace_back(B, W[i]); // 右边界事件}// 按事件点位置排序(后续按顺序处理区间)sort(events.begin(), events.end());// 初始总斜率K:总移动时间关于c的导数// 当c非常小时(远小于所有A和B),所有人都需要右移,移动时间总和为 sum(W[i]*(P[i] - c - D[i]))// 对c求导得总斜率为 -sum(W[i])(因为每个项的导数是 -W[i])ll K = -sum_W;ll x_prev = -1e18; // 上一个事件点的位置(初始为负无穷)// 遍历所有事件点,寻找总斜率由负变正的转折点for (size_t i = 0; i < events.size(); ++i) {ll x = events[i].x; // 当前事件点位置// 当总斜率K >= 0时,说明当前区间的左端点x_prev到当前x之间的c值,总移动时间最小// 因为总移动时间是分段线性函数,当斜率由负变正时,最小值出现在斜率为0的区间if (K >= 0) {ll c = x_prev; // 取区间左端点(或区间内任意整数,结果相同)ll total = 0; // 总移动时间// 计算每个人的移动时间for (int j = 0; j < N; ++j) {ll A_j = P[j] - D[j]; // 第j个人的听力左边界ll B_j = P[j] + D[j]; // 第j个人的听力右边界// c在听力范围左侧:需要移动到A_j(即c-D[j]),移动距离为 (A_j - P[j]) = (c - D[j] - P[j])?不,原逻辑可能需要重新核对// 注意:原问题中,当音乐会位置是c时,此人的听力范围是 [c - D[j], c + D[j]]// 所以正确的判断是:// 如果 P[j] < c - D[j]:此人需要右移到c - D[j],移动距离 = (c - D[j] - P[j])// 如果 P[j] > c + D[j]:此人需要左移到c + D[j],移动距离 = (P[j] - (c + D[j]))// 如果在范围内:移动距离0// 但原代码中的计算逻辑可能存在笔误,正确的计算应为:if (c < (c - D[j])) { // 这显然不可能,原代码可能将A和B定义为相对于P[j]的边界?// 重新理解原事件点的定义:// 原代码中的A = P[i] - D[i],B = P[i] + D[i],这实际是当c的听力范围覆盖P[i]时的c的边界// 例如,当c >= A(即c >= P[i]-D[i])时,P[i]可能进入听力范围左侧;当c <= B(即c <= P[i]+D[i])时,P[i]可能进入听力范围右侧// 可能原代码的事件点定义是:当c超过A时,该人的移动时间斜率变化;当c超过B时,斜率再次变化// 因此,正确的移动时间计算应为:if (c < A_j) { // 音乐会位置c在A_j左侧(即c < P[j]-D[j]):此人的听力范围左边界是c-D[j],但P[j]在更左,所以需要右移到c-D[j]total += W[j] * (c - D[j] - P[j]); // 移动距离 = (c-D[j] - P[j]),时间=距离*速度W[j](注意:W是秒每米,所以时间=距离*W)} else if (c > B_j) { // 音乐会位置c在B_j右侧(即c > P[j]+D[j]):此人的听力范围右边界是c+D[j],但P[j]在更右,需要左移到c+D[j]total += W[j] * (P[j] - (c + D[j])); // 移动距离 = (P[j] - (c+D[j])),时间=距离*W[j]}// 否则(c在[A_j, B_j]之间):P[j]在听力范围内,移动距离0,时间0}cout << total << endl; // 输出最小总时间return 0;}K += events[i].delta; // 处理当前事件点,更新总斜率(遇到事件点后,斜率增加delta)x_prev = x; // 记录上一个事件点位置}// 遍历完所有事件点后,检查是否还有K>=0的情况(理论上应该已经处理)if (K >= 0) {ll c = x_prev;ll total = 0;for (int j = 0; j < N; ++j) {ll A_j = P[j] - D[j];ll B_j = P[j] + D[j];if (c < A_j) {total += W[j] * (c - D[j] - P[j]);} else if (c > B_j) {total += W[j] * (P[j] - (c + D[j]));}}cout << total << endl;}return 0;
}代码解释
-
输入处理:
- 读取输入数据,包括人数
N和每个人的位置P_i、速度W_i、听力距离D_i。
- 读取输入数据,包括人数
-
事件点收集:
- 收集每个听力范围的左右边界作为事件点,并记录每个事件点对总斜率的贡献。
-
排序和斜率计算:
- 对事件点排序,计算初始总斜率
K(初始为所有速度的负值和)。
- 对事件点排序,计算初始总斜率
-
寻找最小时间区间:
- 遍历事件点,维护当前总斜率
K,找到第一个总斜率非负的区间。
- 遍历事件点,维护当前总斜率
-
计算最小时间:
- 在找到的区间内取左端点
c,计算总移动时间并输出。
- 在找到的区间内取左端点
该方法通过分析总移动时间的分段线性特性,高效地找到最小值点,确保了算法的时间复杂度和正确性。
相关文章:

【洛谷 P9025】 [CCC2021 S3] Lunch Concert 题解
题目: 洛谷 P9025 分析: 为了解决这个问题,我们需要找到一个整数位置 c 来举办音乐会,使得所有人移动到能听到音乐会的位置的时间总和最小。每个人移动后的位置应该在其听力范围内,并且尽可能靠近自己的初始位置以减少…...

Python 包管理工具核心指令uvx解析
uvx 是 Python 包管理工具 uv 的重要组成部分,主要用于在隔离环境中快速运行 Python 命令行工具或脚本,无需永久安装工具包。以下是其核心功能和使用场景的详细解析: 一、uvx 的定位与核心功能 工具执行器的角色 uvx 是 uv tool run 的别名&a…...

苍穹外卖05 Redis常用命令在Java中操作Redis_Spring Data Redis使用方式店铺营业状态设置
2-8 Redis常用命令 02 02-Redis入门 ctrlc :快捷结束进程 配置密码: 以后再启动客户端的时候就需要进行密码的配置了。使用-a 在图形化界面中创建链接: 启动成功了。 03 03-Redis常用数据类型 04 04-Redis常用命令_字符串操作命令 05 05-Redis常用命令…...

AI工程师系列——面向copilot编程
前言 笔者已经使用copilot协助开发有一段时间了,但一直没有总结一个协助代码开发的案例,特别是怎么问copilot,按照什么顺序问,哪些方面可以高效的生成需要的代码,这一次,笔者以IP解析需求为例,沉淀一个实践案例,供大家参考 当然,其实也不局限于copilot本身,类似…...

【竖排繁体识别】如何将竖排繁体图片文字识别转横排繁体,转横排简体导出文本文档,基于WPF和腾讯OCR的实现方案
一、应用场景 在古籍数字化、繁体文档处理、两岸三地文化交流等场景中,经常需要将竖排繁体文字转换为横排文字。例如: 古籍研究人员需要将竖排繁体文献转换为现代横排简体格式以便编辑和研究出版行业需要将繁体竖排排版转换为简体横排格式两岸三地交流中需要将繁体竖排文档转…...

梳理Spring Boot中三种异常处理
在 Spring Boot 中处理异常确实有多个方式,比如使用 ControllerAdvice、 BasicErrorController、HandlerExceptionResolver等。不同方式适合不同的场景,下面是对这些方式的分析以及如何选择的建议: 🧩 1. ControllerAdvice Exce…...

NFS服务器实验
实验要求 架设一台NFS服务器,并按照以下要求配置 1、开放/nfs/shared目录,供所有用户查询资料 2、开放/nfs/upload目录,为192.168.xxx.0/24网段主机可以上传目录,并将所有用户及所属的组映射为nfs-upload,其UID和GID均为210 3…...

ffmpeg 转换视频格式
使用FFmpeg将视频转换为MP4格式的常用命令: ffmpeg -i input.mov -c:v libx264 -crf 23 -c:a aac output.mp4 -i input.avi:指定输入文件 -c:v libx264:使用H.264视频编码器 -crf 23:控制视频质量(范围18-28&#…...

Java进阶之新特性
Java新特性 参考 官网:https://docs.oracle.com/en/ JDK5新特性 1.自动装箱与拆箱 自动装箱的过程:每当需要一种类型的对象时,这种基本类型就自动地封装到与它相同类型的包装类中。 自动拆箱的过程:每当需要一个值时…...

Python基础学习-Day32
面对一个全新的官方库,是否可以借助官方文档的写法了解其如何使用。 我们以pdpbox这个机器学习解释性库来介绍如何使用官方文档。 大多数 Python 库都会有官方文档,里面包含了函数的详细说明、用法示例以及版本兼容性信息。 通常查询方式包含以下2种&…...

离线服务器算法部署环境配置
本文将详细记录我如何为一台全新的离线服务器配置必要的运行环境,包括基础编译工具、NVIDIA显卡驱动以及NVIDIA-Docker,以便顺利部署深度学习算法。 前提条件: 目标离线服务器已安装操作系统(本文以Ubuntu 18.04为例)…...

AIGC工具平台-卡通图片2D转绘3D
本模块是一款智能化的2D转3D图像处理工具,能够将卡通风格的2D图片自动转换为高质量3D渲染模型,让平面图像焕发立体生机。借助先进的AI深度学习算法,该工具可以精准识别角色轮廓、光影关系、材质纹理等关键元素,自动生成逼真的3D形…...

docker 启动一个python环境的项目dockerfile版本
文件格式 /home/py/docker/ # 项目根目录 ├── Dockerfile # Docker 构建文件 ├── requirements.txt # Python 依赖清单 └── src/ # 项目代码目录└── api_mock.py # Flask 应用入口文件Dockerfile # 使用…...

Java虚拟机 -方法调用
方法调用 方法调用静态链接动态链接案例虚方法与非虚方法虚方法(Virtual Method)非虚方法(Non-Virtual Method) 方法返回地址 方法调用 我们编写Java程序的时候,我们自己写的类通常不仅仅是调用自己本类的方法。调用别…...

基于matlabcd7.x的无网格近似方法
无网格近似方法(Meshless Methods)是一类数值计算方法,用于解决偏微分方程(PDEs)问题,特别是在几何形状复杂或需要动态网格更新的场景中。与传统的有限元方法(FEM)相比,无…...
JMeter JDBC请求Query Type实测(金仓数据库版)
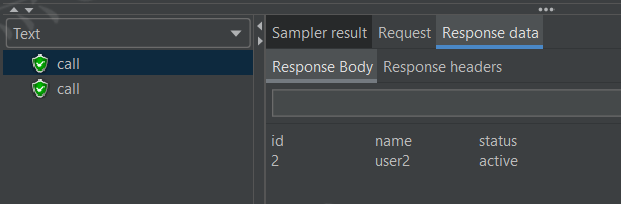
文章目的 在实际性能测试中,JMeter的JDBC Request组件常用于模拟数据库操作。但许多用户对Query Type参数的具体行为存在疑惑。 本文将以金仓数据库KingbaseES为例,通过实测验证每种Query Type的行为,帮助用户明确其使用场景和限制ÿ…...

【内部教程】ISOLAR-AB配置以太网栈|超详细实战版
目录 往期推荐 缩写与定义 关于系统描述(System Description) 1.1 EthCommunicationController 1.2 EthCommunicationConnector 1.2.1 Ports(端口) 1.3 EthPhysicalChannel(以太网物理通道) 1.3.1…...

哈希表和容器中添加元素的方法
push_back v.s. emplace_back: 两者都是在容器末尾添加元素的方法,但是push_back会创建临时对象并进行拷贝构造,而emplace_back是直接构造 //push_back std::vector<MyClass> vec1; MyClass obj1("Object1", 1);//创建一个obj1对象 ve…...

Nginx 核心功能
目录 一:正向代理 1:编译安装 Nginx (1)安装支持软件 (2)创建运行用户、组和日志目录 (3)编译安装 Nginx (4)添加 Nginx 系统服务 2:配置正…...
-高效字符串拼接)
String.join()-高效字符串拼接
String.join-高效字符串拼接 前言一、基础用法:拼接数组或集合元素(仅分隔符)语法示例 1:拼接字符串数组示例 2:拼接集合元素注意事项 二、进阶用法:结合 Stream API 处理复杂场景示例 1:添加前…...

【Canvas与图标】圆角方块蓝星CSS图标
【成图】 120*120的png图标 大小图: 【代码】 <!DOCTYPE html> <html lang"utf-8"> <meta http-equiv"Content-Type" content"text/html; charsetutf-8"/> <head><title>圆角方块蓝星CSS Draft1</…...
 : 何时开始性能分析)
系统性能分析基本概念(5) : 何时开始性能分析
决定何时开始系统性能优化(Performance Optimization)需要根据系统状态、业务需求和资源可用性来判断。以下是触发性能优化的关键场景和时机,结合系统性能分析(如DRAM读取吞吐量等)的背景,保持简洁且实用&a…...

Python实现Web请求与响应
目录 一、Web 请求与响应基础 (一)Web 请求与响应的定义与组成 (二)HTTP 协议概述 (三)常见的 HTTP 状态码 二、Python 的 requests 库 (一)安装 requests 库 (二…...

机器学习 day05
文章目录 前言一、模型选择与调优1.交叉验证2.超参数搜索 前言 通过今天的学习,我掌握了机器学习中模型的选择与调优,包括交叉验证,超参数搜索的概念与基本用法。 一、模型选择与调优 模型的选择与调优有许多方法,这里主要介绍较…...

CentOS Stream安装MinIO教程
1. 下载 MinIO 二进制文件 # 进入 MinIO 安装目录 sudo cd /usr/local/bin/# 下载 MinIO 二进制文件(替换为最新版本链接) wget https://dl.min.io/server/minio/release/linux-amd64/minio chmod x minio2. 创建专用用户和存储目录 # 创建 minio 用户…...

C#新建打开文件对话框
这是Winform直接封装好的打开文件对话框 using System.Windows.Forms; public static string OpenFile(string path) {OpenFileDialog openFileDialog new OpenFileDialog();// 设置对话框属性openFileDialog.Title "选择文件";openFileDialog.InitialDirectory …...

汇川PLC通过开疆智能Profinet转ModbusTCP网关读取西门子PLC数据案例
本案例是客户通过开疆智能Profient转ModbusTCP网关连接汇川PLC的配置案例 Modbus TCP主站即Modbus TCP客户端,Modbus TCP主站最多支持同时与31个Modbus TCP从站 。(Modbus TCP服务器)进行通信。 第一步设置PLC IP地址; 默认PLC…...
零基础入门:MinerU 和 PyTorch、CUDA的关系
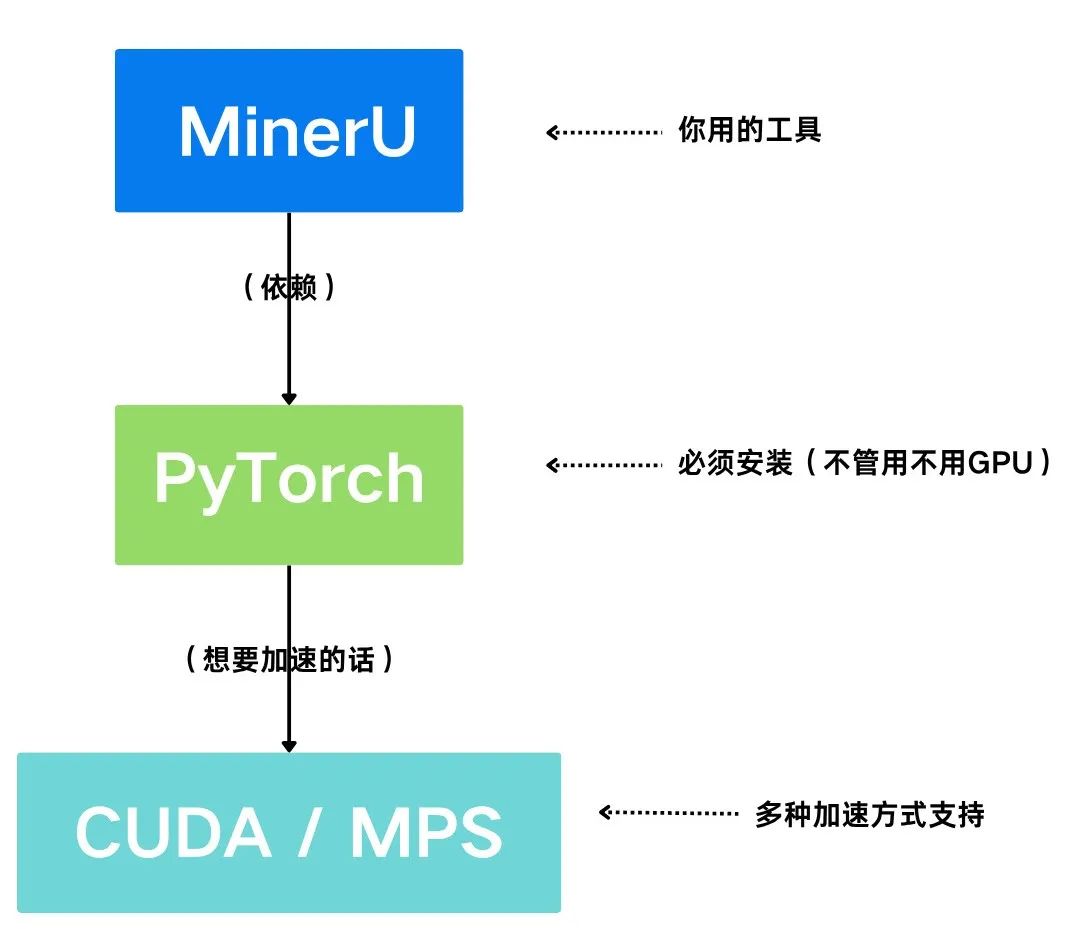
💡一句话总结:MinerU 是一个用 PyTorch 跑模型的程序,PyTorch 支持多种加速方式(如 CUDA、MPS),让它跑得快就需要依赖这些加速工具。 PyTorch官网安装教程(可根据系统情况选择不同版本…...

借助IEDA ,Git版本管理工具快速入门
01 引言 一直使用SVN作为版本管理工具,直到公司新来的一批同事,看到我们使用的SVN都纷纷吐槽,什么年代了,还使用SVN。聊下来,才知道人家公司早早就将SVN切成了Git工具,并吐槽SVN的各种弊端。 既然新的技术…...

三维空间,毫秒即达:RTMP|RTSP播放器在Unity中的落地实现
有人问我:在 Unity 里做超低延迟的直播播放,是什么感觉? 我说,是把一帧帧流动的时间,嵌进一个三维的空间里。 它不属于现在,也不属于过去。 它属于“实时”——属于那一秒内刚刚发生,却已被你看…...
