高等数学-积分
一、不定积分
定理:如果函数f(x)在区间I上连续,那么f(x)在区间I上一定有原函数,即一定存在区间I上的可导函数F(x),使得F'(x)=f(x) ,x∈I
简单地说:连续函数必有原函数。



极限lim*0->x {[∫*0^x sin(t^2)dt]/x^3}=1/3
变上限积分∫*π/2^x (sint/t)'dt=(sinx)/x-π/2
注:(1)若等式两边函数相等(自变量都是x),则等号两边同时求不定积分,等号仍成立。
例:
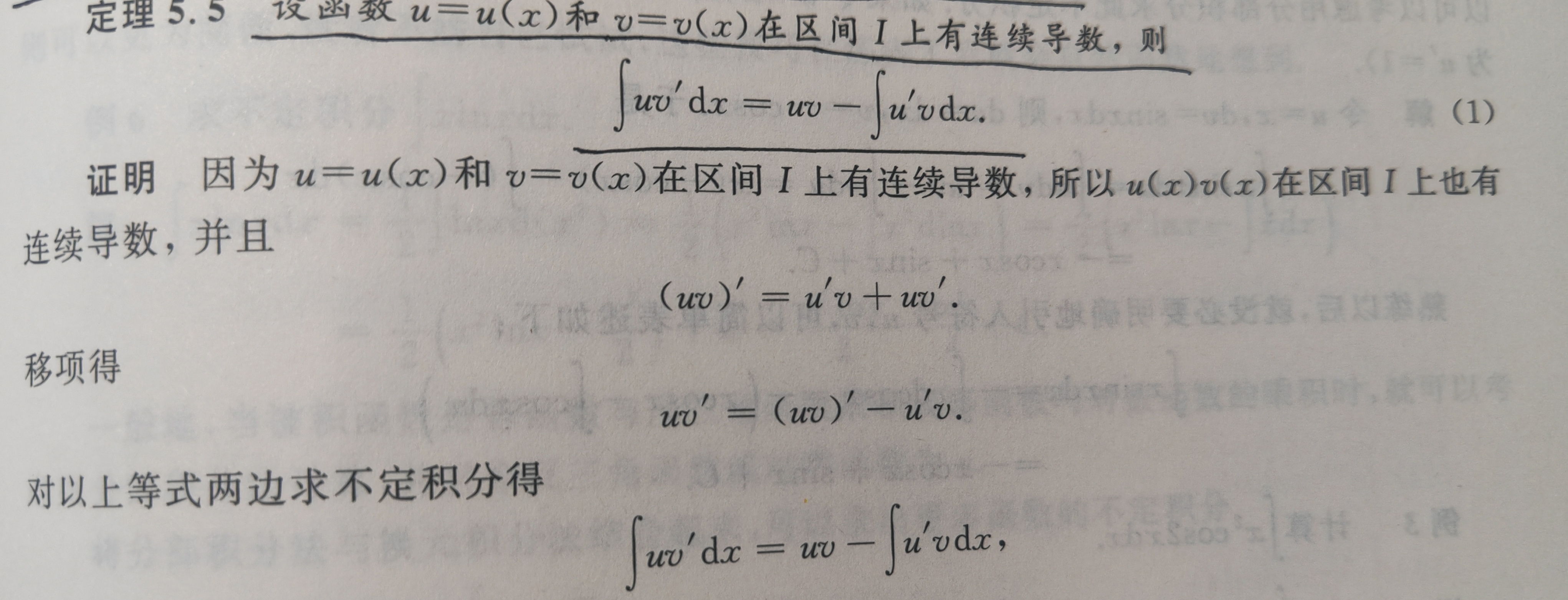
(2)积分是逆转求导:∫(dy/dx) dx=y
二、定积分
(1)可积的两个充分条件:
定理1:设函数f(x)在区间[a,b]上连续,则f(x)在[a,b]上可积。
定理2:设函数f(x)在区间[a,b]上有界,并且只有有限个间断点,则f(x)在[a,b]上可积。
如不作特别的说明,往后总假定所讨论的定积分是存在的。
(2)定积分的基本性质

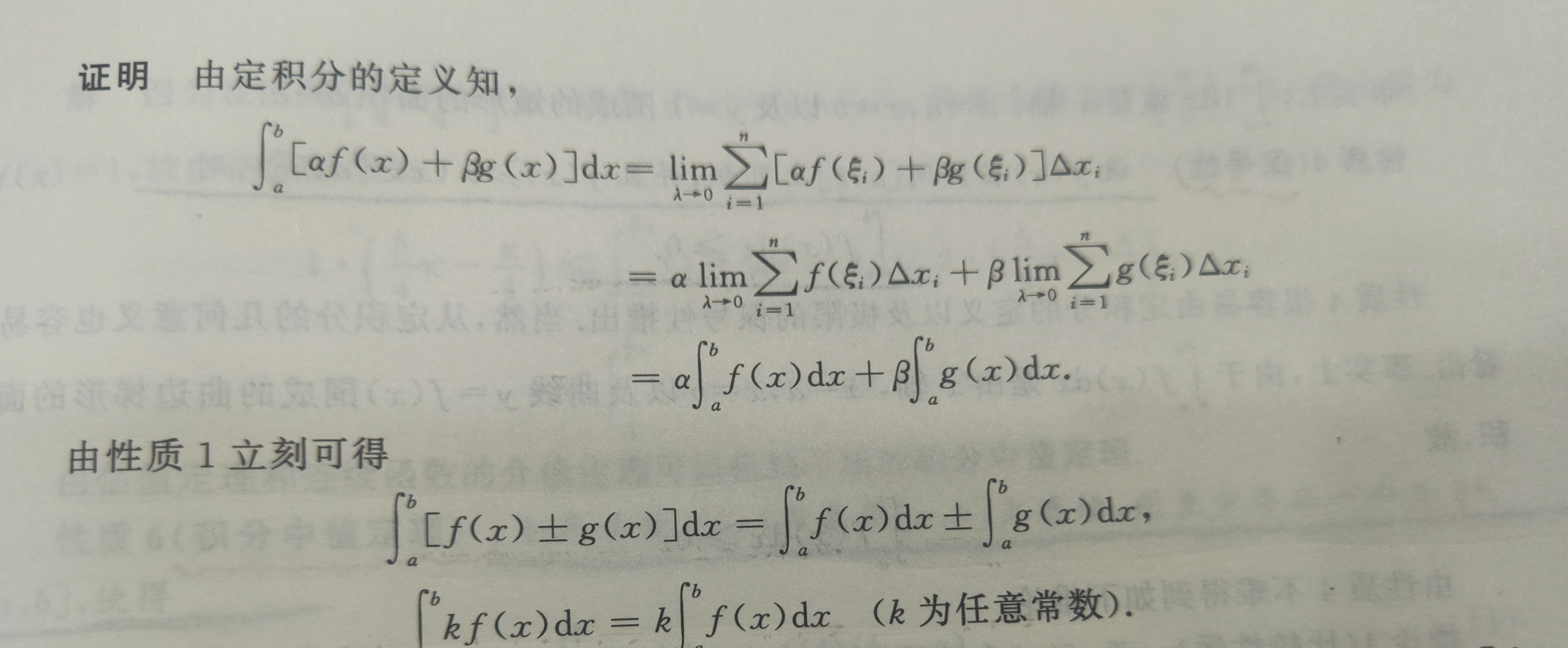




 (3)定积分的换元法与分部积分法
(3)定积分的换元法与分部积分法
a.换元法

该定理告诉我们:在一定条件下,dx可以作为微分记号来对待,即应用换元公式(1)时,如果将积分变量x换为φ(x),则dx就换成φ'(t)dt,这正好是函数x=φ(t)的微分
注:
1)换元必换限,上限对上限,下限对下限,即如果用x=φ(t)把原来的变量换成了新变量t,积分限也必须换成新变量t的积分限,并且原来下限对应的参数做下限,原来上限对应的参数做上限。
2)不要求x=φ(t)单调,从而其反函数也可以不存在。
b.分部积分法

例1:
1/3y^3*e^(-y^2)求原函数?

例2:
-2∫*0^2π asin2a da=acos2a |*0^2π-∫*0^2π cos2a da
三、微积分基本公式
(1)变上限积分

变上限积分求导证明??
(2)微积分学基本公式(牛莱公式):
设函数f(x)在区间[a,b]上连续,F(x)是f(x)在[a,b]上的一个原函数,则∫*a^b f(x)dx=F(b)-F(a).
证明:由已知及2中的定理,函数F(x)和Φ(x)=∫*a^x f(t)dt都是函数f(x)在区间[a,b]上的原函数,从而F(x)-Φ(x)=C(x∈[a,b]),其中C为一个常数。
令x=a得F(a)-Φ(a)=C.又由于Φ(a)=0,所以C=F(a),代入上式得Φ(x)=F(x)-F(a)(x∈[a,b]),即∫*a^x f(t)dt=F(x)-F(a)(x∈[a,b]).特别地,当x=b时,即有∫*a^b f(x)dx=F(b)-F(a).
该公式又可以写成:
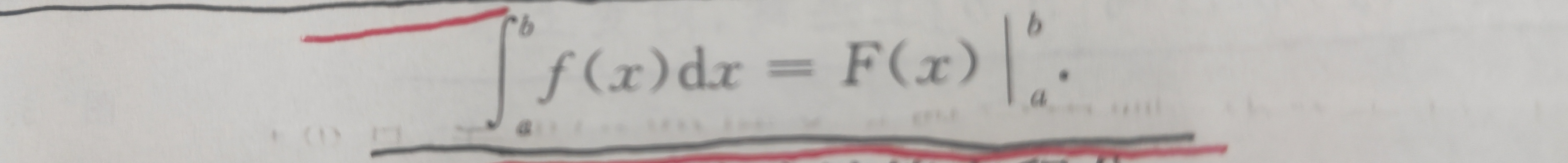
这个公式告诉我们:要计算连续函数f(x)的定积分
,只需先求出f(x)的任何一个原函数F(x),然后将F(x)在积分上限的值减去F(x)在积分下限的值即可。
四、求定积分
1)∫*0^π/2 (sinx)^2cosxdx=∫0^π/2 (sinx)^2dsinx=1/3(sinx)^3 |0^π/2=1/3
2)∫*0^1/2 dx/[√x(1-x)]=∫*0^1/2 [1/√(1-x)*]·1/√xdx=2∫*0^1/2 d(√x)/[1-(√x)^2]=2arcsin(√x) |*0^1/2=2arcsin(√2/2)=π/2
五、二重积分
(1)二重积分的性质:


例1:
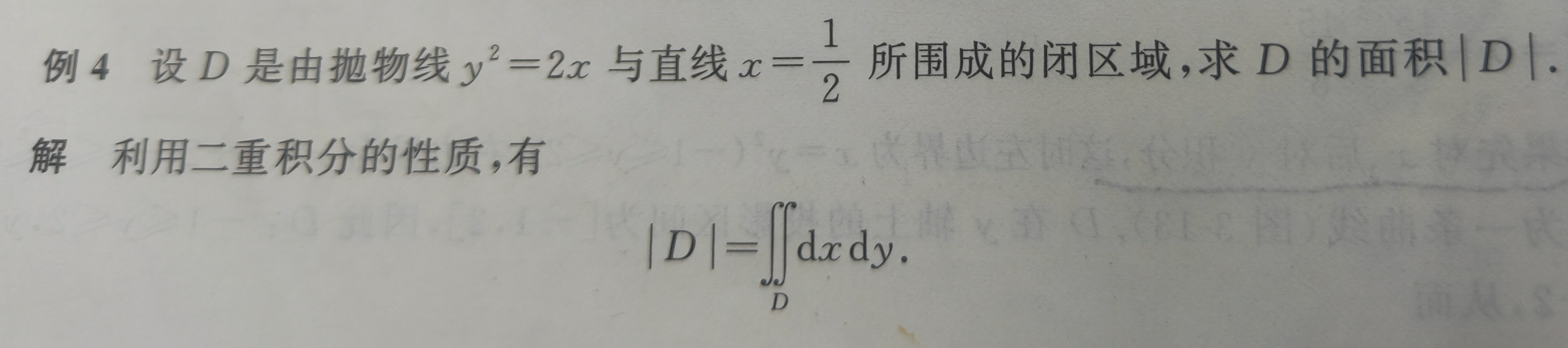

 例2:
例2:
利用二重积分计算下面图形的面积:由抛物线y^=2x与直线y=x-4所围成的平面图形。
解:
解方程组得到抛物线y^=2x与直线y=x-4的两个交点为(2,-2),(8,4)
先对x、后对y积分:
被积区域:-2
平面图形的面积:∫∫1dxdy=∫*-2^4 dy∫*(y^2)/2^(y+4) dx=∫*-2^4 [(y+4)-(y^2)/2]dy=18
当被积函数f(x,y)=1时,计算二重积分就相当于计算被积区域的面积
(2)极坐标
一般来说,当积分区域D为圆形、扇形、或环形闭区域时,而被积函数含有x^2+y^2或者arctan(y/x)等式子时,用极坐标计算二重积分往往比较简单。

注:[(sina)^3]'=1/3[cosa)^3]-cosa
结论:(1)∫0->+∞* e^[-x^2]dx=(√π)/2
(2)∫-∞->+∞* e^[-x^2]dx=√π
六、三重积分
(1)对称奇偶性

(2)三重积分的计算

(3)[d(e^-∫P(x)dx)]/dx=-P(x)e^-∫P(x)dx
相关文章:

高等数学-积分
一、不定积分 定理:如果函数f(x)在区间I上连续,那么f(x)在区间I上一定有原函数,即一定存在区间I上的可导函数F(x),使得F(x)f(x) ,x∈I 简单地说:连续函数必有原函数。 极限lim*0->x {[∫*0^x sin(t^2)…...

IOS平台Unity3D AOT全局模块结构分析
分析背景 由于IOS平台中不允许执行动态代码,Unity 4.6之前的版本在IOS平台中采用了AOT的处理方式,提前将C#代码静态编译为机器识别的二进制机器码。Unity引擎4.6之前的版本中IOS框架采用了Mono的AOT机制实现静态编译和处理,本文针对全局AOT模…...

Vue 3.0中自定义指令
自定义指令是增强 Vue 组件的重要手段。常见的内置指令有: v-if、v-show、v-model、v-bind、v-on等。 本文将详细讲解如何创建和使用自定义指令,关注以下几个关键点: 1. 指令的钩子函数:类似于生命周期钩子函数。 2. 指令钩子函…...

在 语义分割 和 图像分类 任务中,image、label 和 output 的形状会有所不同。
1. 图像分类 (Image Classification) 图像分类 任务是将整个图像分类为一个类别。通常,output 是对整个图像的类别的预测,而 label 是该图像的真实类别。 1.1 image 的形状 image 是输入图像数据,通常是一个四维张量: 形状&…...

C++面试4-sizeof解析
C++sizeof关键字的深度解析 一、本质认知:编译器的尺度 1. 编译期操作符的基因 int arr[5]; cout << sizeof(arr); // 输出20(假设int为4字节)非运行时特性:在编译阶段完成计算,不会生成任何机器指令表达式不求值:sizeof(++i)不会改变i的值类型感知:对类型名使…...

CyberSecAsia专访CertiK首席安全官:区块链行业亟需“安全优先”开发范式
近日,权威网络安全媒体CyberSecAsia发布了对CertiK首席安全官Wang Tielei博士的专访,双方围绕企业在进军区块链领域时所面临的关键安全风险与防御策略展开深入探讨。 Wang博士在采访中指出,跨链桥攻击、智能合约漏洞以及私钥管理不当&#x…...

uniapp如何设置uni.request可变请求ip地址
文章目录 简介方法一:直接在请求URL中嵌入变量方法二:使用全局变量方法三:使用环境变量方法四:服务端配置方法五:使用配置文件(如config.js):总结 简介 在uni-app中,uni.request 用…...

文件操作和IO-3 文件内容的读写
文件内容的读写——数据流 流是操作系统提供的概念,Java对操作系统的流进行了封装。 数据流就像水流,生生不息,绵延不断。 水流的特点:比如要100mL的水,可以一次接10mL,分10次接完,也可以一次接…...

架构的设计
搭建架构的最低前提 1.设计清晰: 需求文档: 有哪些界面 每个界面提够了哪些功能 这些功能是怎样操作的 会有哪些反馈 2.技术: 写架构的同学:这次项目设计的技术 都要有料及(用到的技术有哪些特点 有哪些缺点&…...
SpringAI 大模型应用开发篇-SpringAI 项目的新手入门知识
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 1.0 SpringAI 概述 目前大模型应用开发最常见的框架就是 LangChain,然而 LangChain 是基于 Python 语言,虽然有 LangChain4j,但是对于大量使…...
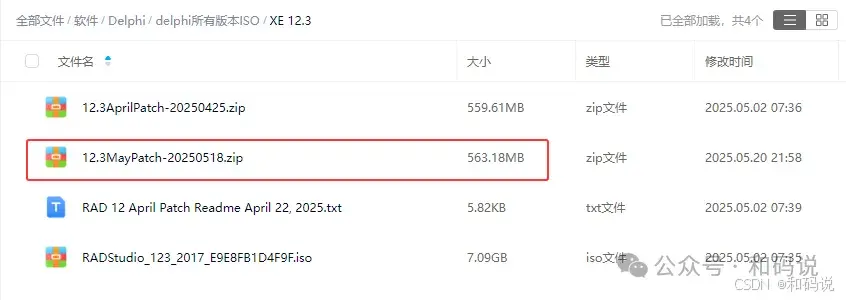
编程速递-RAD Studio 12.3 Athens五月补丁:May Patch Available
编程速递-RAD Studio 12.3 Athens四月补丁:关注软件性能的开发者,安装此补丁十分必要 今天 (2025 年 5 月 19 日)Embarcadero 发布了 RAD Studio、Delphi 和 CBuilder 12.3 Athens(雅典)的第二个补丁。 RA…...
)
Vue3实现轮播表(表格滚动)
在这之前,写过一篇Vue2实现该效果的博文:vue-seamless-scroll(一个简单的基于vue.js的无缝滚动) 有兴趣也可以去看下,这篇是用vue3实现,其实很简单,目的是方便后面用到直接复制既可以了。 安装: <...
Python爬虫高阶:动态页面破解与验证码OCR识别全流程实战)
Python爬虫(33)Python爬虫高阶:动态页面破解与验证码OCR识别全流程实战
目录 一、技术背景与行业痛点二、核心技术与实现路径2.1 动态页面处理方案对比2.2 Selenium深度集成实践2.3 OCR验证码破解方案1. 预处理阶段:2. 识别阶段:3. 后处理阶段 三、典型应用场景解析3.1 电商价格监控系统1. 技术架构2. 实现效果 3.2 社交媒体舆…...

Matlab学习合集
1.变量 2.常见的数学函数 3. 向量 向量的创建: 直接创建:针对于数量少的情况 冒号法 函数创建:...

基于labview的声音采集与存储分析系统
基于LabVIEW的声音信号采集与存储分析系统开发实战:从原理到代码实现 (内含源码)基于labview的声音采集与处理系统 点击跳转工坊 点击跳转视频 引言 在音频技术与工业监测领域,声音信号的实时采集与分析是一项基础且关键的任务。…...

【项目记录】部门增删改及日志技术
1 删除部门 1.1 需求 删除部门数据。在点击 "删除" 按钮,会根据ID删除部门数据。 了解了需求之后,我们再看看接口文档中,关于删除部门的接口的描述,然后根据接口文档进行服务端接口的开发。 1.2 接口描述 1.2.1 基…...

TDengine 更多安全策略
简介 上一节我们介绍了 TDengine 安全部署配置建议,除了传统的这些配置外,TDengine 还有其他的安全策略,例如 IP 白名单、审计日志、数据加密等,这些都是 TDengine Enterprise 特有功能,其中白名单功能在 3.2.0.0 版本…...

电子制造企业智能制造升级:MES系统应用深度解析
在全球电子信息产业深度变革的2025年,我国电子信息制造业正经历着增长与转型的双重考验。据权威数据显示,2025年一季度行业增加值同比增长11.5%,但智能手机等消费电子产量同比下降1.1%,市场竞争白热化趋势显著。叠加关税政策调整、…...

Java使用Collections集合工具类
1、Collections 集合工具类 Java 中的 Collections 是一个非常有用的工具类,它提供了许多静态方法来操作或返回集合。这个类位于 java.util 包中,主要包含对集合进行操作的方法,比如排序、搜索、线程安全化等。 Java集合工具类的使用&#x…...

磁盘空间不足,迁移Docker 数据目录
停止 Docker 服务。 sudo systemctl stop docker 将现有的 Docker 数据移动到新位置(例如 /home/docker-data)。 sudo mv /var/lib/docker /home/docker-data 在原位置创建一个指向新位置的符号链接。 sudo ln -s /home/docker-data /var/lib/dock…...

python打卡day33
知识点回顾: PyTorch和cuda的安装查看显卡信息的命令行命令(cmd中使用)cuda的检查简单神经网络的流程 数据预处理(归一化、转换成张量)模型的定义 继承nn.Module类定义每一个层定义前向传播流程 定义损失函数和优化器定…...

目标检测新突破:用MSBlock打造更强YOLOv8
文章目录 YOLOv8的现状与挑战YOLO-MS的MSBlock简介MSBlock的工作原理MSBlock的优势利用MSBlock改进YOLOv8替换YOLOv8主干网络中的部分模块代码实现:替换CSP模块为MSBlock在YOLOv8的颈部(Neck)中插入MSBlock代码实现:在颈部区域插入MSBlock实验结果与分析实验设置性能对比性…...
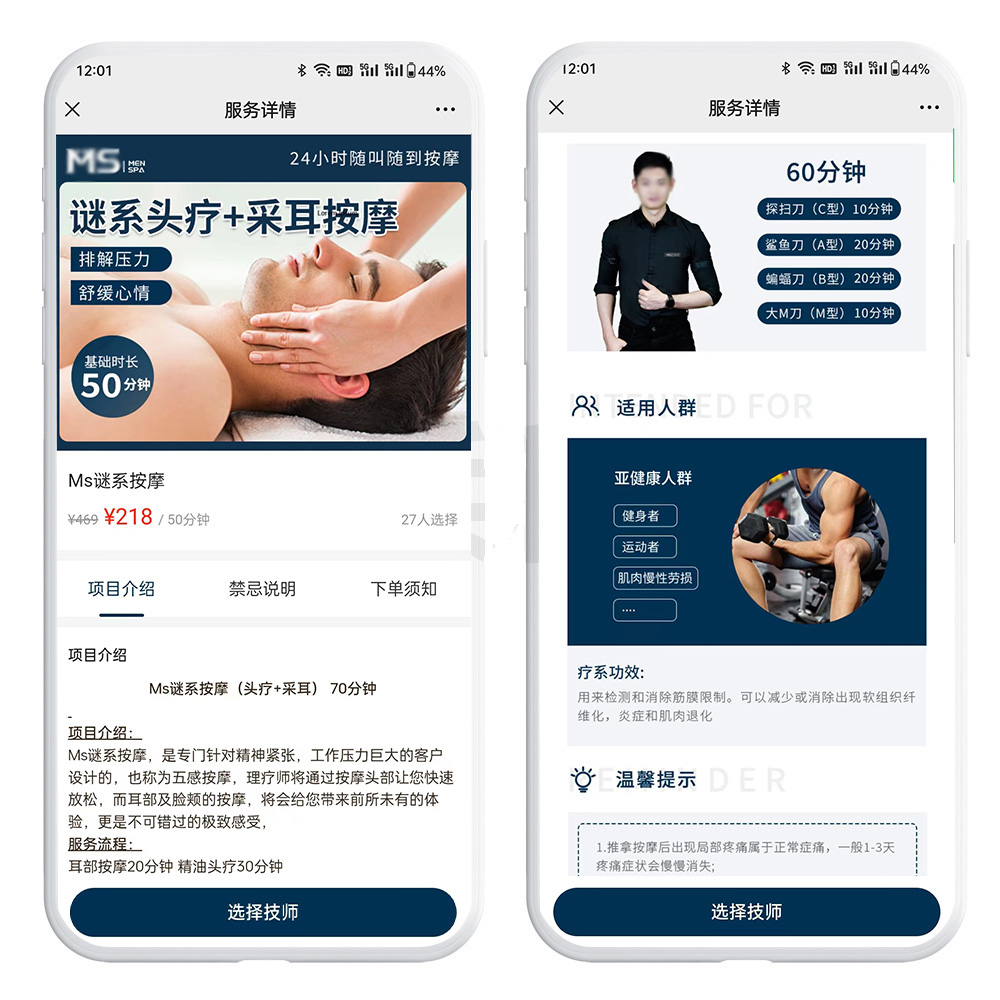
同城上门预约服务系统案例分享,上门服务到家系统都有什么功能?这个功能,很重要!
你以为上门按摩这类平台只要做好接单派单就万事大吉了?大错特错!市面上90%的系统只会吹嘘基础功能,却对最关键的财税问题避而不谈。很多创业者直到被税务稽查才发现,自己每年都在白白多交几倍的冤枉税!举个例子&#x…...
)
docker面试题(5)
Docker安全么 Docker 利用了 Linux 内核中很多安全特性来保证不同容器之间的隔离,并且通过签名机制来对镜像进行 验证。大量生产环境的部署证明,Docker 虽然隔离性无法与虚拟机相比,但仍然具有极高的安全性。 如何清理后台停止的容器 可以使用…...

为什么需要在循环里fetch?
假设有多个设备连接在后端,数量不定,需要按个读回状态,那么就要在循环里fetch了. 此函数非常好用,来自于国内一个作者,时间久了,忘记了来源,抱歉. export default async function fetchWithTimeout(resource, options {}) {const { timeout 1000 } options;const controll…...

用 UniApp 开发 TilePuzzle:一个由 CodeBuddy 主动驱动的拼图小游戏
我正在参加CodeBuddy「首席试玩官」内容创作大赛,本文所使用的 CodeBuddy 免费下载链接:腾讯云代码助手 CodeBuddy - AI 时代的智能编程伙伴 起心动念:从一个小游戏想法开始 最近在使用 UniApp 做练手项目的时候,我萌生了一个小小…...

HJ101 输入整型数组和排序标识【牛客网】
文章目录 零、原题链接一、题目描述二、测试用例三、解题思路四、参考代码 零、原题链接 HJ101 输入整型数组和排序标识 一、题目描述 二、测试用例 三、解题思路 基本思路: 选择一个排序算法,然后根据标识确定升序还是降序;具体思路&a…...

在Linux debian12系统上使用go语言以及excelize库处理excel数据
go-do-excel 一、介绍 myBook.xlsx表中,B列是“全部IP地址“,A列是“分发成功的IP地址“,本脚本采用go语言编写,通过读取myBook.xlsx中B列“全部IP地址“和A列“分发成功的IP地址“数据,计算出“分发失败的IP地址“数据,将其写入到C列。 二、编程语言 本脚本在Linux De…...

Appium 的 enableMultiWindows 参数
引言 在移动应用自动化测试中,混合应用(Hybrid App) 和多窗口场景(如分屏、弹窗、多 WebView)的处理一直是技术难点。Appium 的 enableMultiWindows 参数为这类场景提供了关键支持,但在实际使用中常…...

【Python/Tkinter】实现程序菜单
程序源码: import tkinter as tk from tkinter.colorchooser import askcolordef set_colour():saskcolor(color"red",title"选择背景色")root.config(bgs[1])class Application(tk.Frame):def __init__(self,masterNone):super().__init__(ma…...
