乘最多水的容器 | 算法 | 给定一个整数数组。有n条垂线。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
在我们日常生活中,蓄水似乎是一个极为朴素的物理行为:两堵墙之间,注入水,看谁能装得更多。可如果换个角度,从算法的视角去看这个问题,它会变得怎样?你是否意识到,这样一个简单的问题背后,隐藏着的是人类在面对“有限资源中寻找最优解”这一命题时,所展现出的智慧与思维模式?

一、从“装水问题”谈起:问题的提出与物理直觉
1.1 题目描述:算法问题的语义抽象
我们被给予一个整数数组 height,其每个元素代表一根垂直于 x 轴的线段的高度。第 i 条线段位于横坐标 i 处。我们要从中选择任意两条线段,以 x 轴为底,线段为侧壁,构成一个“容器”。求这个容器所能容纳的最大水量。
用数学语言表达就是:
给定数组:
我们要找到一对下标 ,使得:
1.2 物理直觉与几何建模
这道题的本质是一道几何问题。我们可以把每个数看作是平面直角坐标系中的一根垂直线段,其底部在 x 轴上。两个线段与 x 轴围成一个矩形槽,槽的高度取决于较短的那根线段,槽的宽度是两个线段之间的距离。
我们要做的,就是找到这样一对线段,使得这个“槽”的面积最大。
这个问题在现实世界中也有对应,比如修建两个挡水坝,在中间蓄水;又比如数据中心的冷却系统设计中,如何在有限结构中最大限度引导冷却液的流动。
二、暴力算法的尝试:最直接但最慢的方案
2.1 暴力破解:穷尽所有可能
最直观的思路是:我们可以枚举所有可能的左右边界组合,然后计算它们围成的面积,最后取最大值。
伪代码如下:
max_area = 0
for i in range(n):for j in range(i + 1, n):area = min(height[i], height[j]) * (j - i)max_area = max(max_area, area)
2.2 时间复杂度分析
这个算法的时间复杂度是 ,因为我们对每一对可能的 (i, j) 都进行了面积计算。在最坏情况下,当 n = 10^5 时,计算量为 ,这是不可接受的。
2.3 空间复杂度
空间复杂度仍为 ,因为我们没有使用额外空间存储结构。
三、数学建模与优化策略
3.1 关键思想:从局部最优走向全局最优
我们可以采用“双指针”策略:设置两个指针,一个从左边开始(left),一个从右边开始(right)。每次计算当前区间组成的容器面积,然后将较短的那一边向中间移动。为什么?因为移动较短边可能找出更高的线段,从而有机会获得更大的面积。
def maxArea(height):left, right = 0, len(height) - 1max_area = 0while left < right:width = right - lefth = min(height[left], height[right])max_area = max(max_area, width * h)if height[left] < height[right]:left += 1else:right -= 1return max_area
3.2 算法的正确性证明
核心逻辑:我们始终从当前最大可能宽度开始,然后不断减小宽度的同时,尝试找到更高的线段提升高度,以挽救面积的损失。
证明思路:
-
假设当前区间是
i到j,高度分别是h_i和h_j,宽度是j - i。 -
如果
h_i < h_j,我们知道以i为左边界,任何再往右的线段h_k(k > i)和h_j组成的容器,其宽度必然小于当前宽度。 -
若我们不移动
i,只移动j,则高度肯定不会高于当前h_i,面积只会变小。 -
因此我们必须移动较短的一边,才有可能找到更高的线段来补偿宽度的损失。
3.3 时间与空间复杂度
-
时间复杂度:,因为每个元素最多被访问一次。
-
空间复杂度:。
四、深度剖析:为什么双指针能带来线性优化?
4.1 双指针的经典应用场景
“双指针”是一种极为重要的算法技巧,常用于:
-
对撞指针(如本题)
-
快慢指针(如链表中找环)
-
滑动窗口(如最大子数组和/最小覆盖子串)
其核心思想是:在有序或可比较结构中,通过两个游走指针节省无谓的枚举,达到线性优化的目的。
4.2 为什么移动较短边更优?
一个深刻的数学事实是:面积的计算是由最短边决定的。如果我们保持较短边不动而移动较长边,我们只是在牺牲宽度的同时保持高度不变,甚至更低。因此,为了可能的提升,总是移动较短边是最优策略。
这是一种贪婪策略:我们每一步都想博取最大提升空间。
4.3 与其他优化策略的对比
-
动态规划不适用:问题不像“最优子结构”那样可以拆解。
-
分治法也不适合:左右分治无法有效组合两个子区间的面积。
-
单调栈虽强大,但本题无需维持单调结构。
这正是双指针大显身手的领域。
五、极限测试与边界思维:算法在实际中的鲁棒性
5.1 极小输入
-
[1, 1]→ 结果为1,边界处理正确。
5.2 极大输入
-
当数组长度为 且元素最大为 时,算法仍能线性时间处理,优越性显著。
5.3 高度全相等
-
[5, 5, 5, 5, 5]→ 选择最远的两个线段,宽度最大,面积为5 * (n-1)。
六、从“装水”到“最优选择”的人类思维模型
6.1 贪婪问题
这道题的本质是一个贪婪问题:每一步都做出当前最优决策,以期达到整体最优。它对应着人类在资源有限的世界中,如何在本地信息指导下做出选择。
6.2 从计算到决策:数学模型的抽象价值
“装水”问题其实是一种资源分配模型:有限的空间,寻找最大利用。这种模型在经济学、运筹学、数据科学中普遍出现。
6.3 短板效应与边界约束
在整个问题中,始终是“较短的那根线”决定着容量。这是著名的“木桶原理”的抽象体现:系统的容量由最短板决定。
七、扩展与变种:问题的泛化与挑战
7.1 三维版本:最大水池问题
给定一个二维矩阵,如何找出围成水池的最大体积?这引出了“接雨水 II”问题。
7.2 动态数据流中的最大容器
如果线段是动态输入的呢?我们能否在滑动窗口中维护最大面积?这里需要引入数据结构,如单调队列。
7.3 多个容器的最大总水量
如果可以选择多个不重叠的容器,如何实现总水量最大?问题转化为区间选择与动态规划的结合。
八、结语
我们不只是为了写一个能通过测试的程序,而是为了培养那种从混沌中提炼规则、从有限中寻找最优的能力。算法,正是这个时代最重要的思维工具之一。
相关文章:

乘最多水的容器 | 算法 | 给定一个整数数组。有n条垂线。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
在我们日常生活中,蓄水似乎是一个极为朴素的物理行为:两堵墙之间,注入水,看谁能装得更多。可如果换个角度,从算法的视角去看这个问题,它会变得怎样?你是否意识到,这样一个简单的问题…...

Python项目文件组织与PyCharm实践:打造高效开发环境
# Python项目文件组织与PyCharm实践:打造高效开发环境 在Python编程的世界里,合理组织项目文件是提升代码质量、增强可维护性以及促进团队协作的关键。同时,借助强大的集成开发环境(IDE)——PyCharm,我们能…...

【Java高阶面经:数据库篇】19、分库分表查询困境:无分库分表键时的高效应对
一、分库分表下的无分片键查询困境 在分布式数据库架构中,分库分表通过分片键(如买家ID)将数据分散存储,显著提升了单表性能和系统扩展性。然而,当业务需要从非分片键维度(如卖家ID)进行查询时,传统架构暴露出以下核心问题: 1.1 跨分片扫描的性能灾难 数据分散性:以…...

spring中的BeanFactoryAware接口详解
一、接口定义与核心作用 BeanFactoryAware 是 Spring 框架提供的一个回调接口,允许 Bean 在初始化阶段获取其所属的 BeanFactory 实例。该接口定义如下: public interface BeanFactoryAware {void setBeanFactory(BeanFactory beanFactory) throws Bea…...

Unity Hub打不开项目一直在加载
Unity Hub打不开项目,一直在加载。 运行环境:win10 解决方法:退还个人许可证,退出UnityHub重新登录后,再次获取个人许可证 Tips: 国内连续超过三天不登陆就需要激活一次。(每天登陆一次会自动续时间吗&…...

蓝桥杯19681 01背包
问题描述 有 N 件物品和一个体积为 M 的背包。第 i 个物品的体积为 vi,价值为 wi。每件物品只能使用一次。 请问可以通过什么样的方式选择物品,使得物品总体积不超过 M 的情况下总价值最大,输出这个最大价值即可。 输入格式 第一行输…...
)
服务器操作系统调优内核参数(方便查询)
fs.aio-max-nr1048576 #此参数限制并发未完成的异步请求数目,应该设置避免I/O子系统故障 fs.file-max1048575 #该参数决定了系统中所允许的文件句柄最大数目,文件句柄设置代表linux系统中可以打开的文件的数量 fs.inotify.max_user_watches8192000 #表…...

ElasticSearch导读
ElasticSearch 简介:ElasticSearch简称ES是一个开源的分布式搜素和数据分析引擎。是使用Java开发并且是当前最流行的开源的企业级搜索引擎,能够达到近实时搜索,它专门设计用于处理大规模的文本数据和实现高性能的全文搜索。它基于 Apache Luc…...

【机器学习】 关于外插修正随机梯度方法的数值实验
1. 随机梯度下降(SGD) 迭代格式: x k 1 x k − η k ∇ f i ( x k ) x_{k1} x_k - \eta_k \nabla f_i(x_k) xk1xk−ηk∇fi(xk) 其中, η k \eta_k ηk 为步长(可能递减), ∇ f…...

结构型:组合模式
目录 1、核心思想 2、实现方式 2.1 模式结构 2.2 实现案例 3、优缺点分析 4、适用场景 1、核心思想 目的:将总是在重复、迭代地显示的某种自相似性的结构(部分与整体结构特征相似),例如树形结构,以统一的方式处…...

windows 删除文件夹提示“操作无法完成,因为其中的文件夹或文件已在另一程序中打开”
windows 删除文件夹提示“操作无法完成,因为其中的文件夹或文件已在另一程序中打开” tomact已经关闭了,刚开始怀疑是tomcat关闭不彻底,但是任务管理器–》进程里根本没有java的进程了,由于是医院服务器、不方便重启 解决方法&am…...

使用 electron-builder 打包与发布 Electron 应用
基于 electron-vite-vue 项目结构 本文将基于 electron-vite-vue 脚手架,详细介绍如何使用 electron-builder 实现: ✅ 多平台打包(Windows / macOS / Linux)✅ 自动更新发布配置✅ 常用构建脚本与输出结构 📁 项目结…...

微信小程序中,解决lottie动画在真机不显示的问题
api部分 export function getRainInfo() {return onlineRequest({url: /ball/recruit/getRainInfo,method: get}); }data存储json数据 data:{rainJson:{} }onLoad方法获取json数据 onLoad(options) {let that thisgetRainInfo().then((res)>{that.setData({r…...
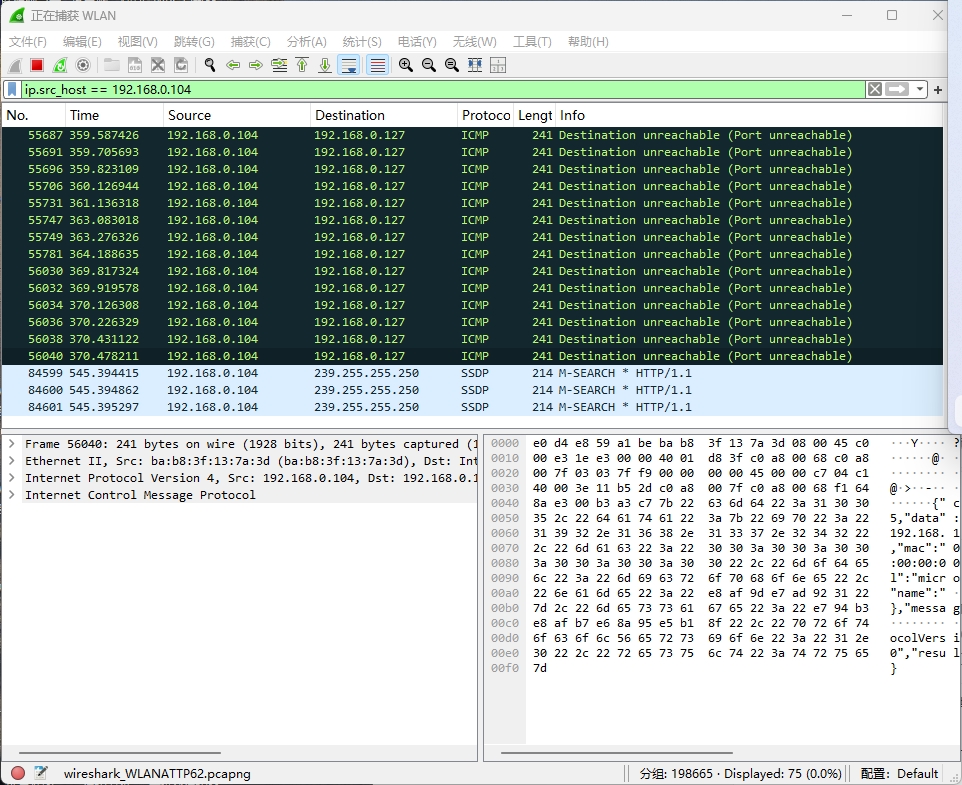
Wireshark 抓包工具使用
1.下载地址 https://2.na.dl.wireshark.org/win64/ 或者 Wireshark Go Deep 2.安装并打开 3.电脑设置热点,手机连接热点 4.手机发起网络请求,工具上选择WLAN。或者本地连接 5.点击查看抓包数据,过滤。最好用发送端ip过滤,s…...

大语言模型(LLM)本身是无状态的,怎么固化记忆
大语言模型(LLM)本身是无状态的,无法直接“记住”历史对话或用户特定信息 大语言模型(LLM)本身是无状态的,无法直接“记住”历史对话或用户特定信息,但可以通过架构改进、外部记忆整合、训练方法优化等方案实现上下文记忆能力。 一、模型内部记忆增强:让LLM“记住”…...

JUC入门(六)
12、四大函数式接口 Consumer<T>(消费者接口) 源码 功能 接收一个参数T,不返回任何结果。主要用于消费操作,例如打印日志、更新状态等。 使用场景 遍历集合并执行操作。 对象的字段赋值。 代码示例 import java.util.…...

std::chrono类的简单使用实例及分析
author: hjjdebug date: 2025年 05月 20日 星期二 14:36:17 CST descrip: std::chrono类的简单使用实例及分析 文章目录 1.实例代码:2. 代码分析:2.1 auto t1 std::chrono::high_resolution_clock::now();2.1.1 什么是 system_clock2.1.2 什么是 chrono::time_point?2.1.3 什…...
)
Git命令汇总(自用,持续更新update 5/23)
文章目录 Git常见命令1. 推送空提交2. 提交Clean-PR3. 回退add操作4. 交互式rebase4.1 切换模式4.2 保存与退出4.3 注意Rebase 5. 合并多个commit 问题一:Clone Github报错The TLS connection was non-properly terminated.TLS握手报错原因解决 问题二:F…...

window xampp apache使用腾讯云ssl证书配置https
下载腾讯云ssl证书: 编辑Apache根目录下 conf/httpd.conf 文件: #LoadModule ssl_module modules/mod_ssl.so和#Include conf/extra/httpd-ssl.conf,去掉前面的#号注释。 编辑Apache根目录下 conf/httpd-ssl.conf 文件: <Vi…...

MATLAB求解二元一次方程组基础教程
MATLAB求解二元一次方程组基础教程 一、二元一次方程组简介 二元一次方程组是包含两个未知数(x和y)的一组方程,每个方程中未知数的最高次数为1。一般形式为: a₁x b₁y c₁ a₂x b₂y c₂其中a₁, b₁, c₁, a₂, b₂, c₂为已知系数。 二、MATL…...

Android13 wifi设置国家码详解
Android13 wifi设置国家码详解 文章目录 Android13 wifi设置国家码详解一、前言二、设置wifi国家码相关代码1、adb或者串口也能设置和获取当前国家码(1)查询命令的方式(2)获取和设置国家码的示例 2、Java代码设置国家码3、获取当前…...
逆向音乐APP:Python爬虫获取音乐榜单 (1)
1. 引言 在数字音乐时代,许多平台如音乐有榜单,限制非付费用户访问高音质或独家内容。然而,从技术研究的角度来看,我们可以通过逆向工程和Python爬虫技术解音乐的API接口,获取付费音乐的播放链接。 2. 技术准备 在当…...

JVM 垃圾回收器
以下是对主流 JVM 垃圾回收器的详细解析,涵盖 一、Serial GC(单线程串行回收器) 二、Parallel GC(吞吐量优先回收器) 三、CMS(Concurrent Mark Sweep,低延迟回收器) 四、G1&…...

Java合并两个列表到目标列表,并且进行排序
可以通过使用addAll()方法将两个列表合并到目标列表中。以下是实现代码: java 复制 下载 List<LedgerRecord> rkRecordList warehouseMapper.selectLedgerRkRecordByMaterialNo(materialNo); List<LedgerRecord> ckRecordList warehouseMapper.se…...

Spring AI Alibaba集成阿里云百炼大模型应用
文章目录 1.准备工作2.引入maven依赖3.application.yml4.调用4.1.非流式调用4.2.流式调用 阿里云百炼推出的智能体应用、工作流应用和智能体编排应用,有效解决了大模型在处理私有领域问题、获取最新信息、遵循固定流程以及自动规划复杂项目等方面的局限,…...

22. 用例依赖装饰器的实现思路和方法
22. 用例依赖装饰器的实现思路和方法 一、核心功能解析 1.1 实现目标 depend(casetest_login) # 当test_login失败时跳过当前测试 def test_order(self):pass功能特性: 前置依赖检测自动跳过失效用例异常依赖关系校验实时结果分析 二、代码逐行解析 2.1 自定义…...

支持向量存储:PostgresSQL及pgvector扩展详细安装步骤!老工程接入RAG功能必备!
之前文章和大家分享过,将会出一篇专栏(从电脑装ubuntu系统,到安装ubuntu的常用基础软件:jdk、python、node、nginx、maven、supervisor、minio、docker、git、mysql、redis、postgresql、mq、ollama等),目前…...

【部署】如何离线环境创建docker容器执行python命令行程序
回到目录 【部署】如何离线环境创建docker容器执行python命令行程序 本文以 dify_import项目为例,讲解如何在离线服务器上,搭建docker容器环境,执行python命令行程序 1. 一台有互联网的服务器(ubuntu24.04) 1.1. 拉取一个ubuntu的docker镜…...
idea常用配置 properties中文输出乱码
propertis配置中文乱码 源码和编译后的都是中文 程序输入效果 idea配置3处 程序输出效果 自定义注释模板 IDEA 中有以下两种配置模板。 File and Code Templates Live Templates File and Code Templates File and Code Templates 用来配置文件和代码模板,即…...

【Bluedroid】蓝牙 HID Host connect全流程源码解析
蓝牙 HID(Human Interface Device,人机接口设备)是智能设备与外设(如键盘、鼠标、游戏手柄)交互的核心协议。本文围绕Android蓝牙 HID 主机模块的连接流程,从上层应用发起连接请求开始,逐层解析协议栈内部的状态检查、设备管理、SDP 服务发现、L2CAP 通道建立等关键步骤…...
