CC53.【C++ Cont】一维前缀和
目录
1.定义
2.作用
3.例题:【模板】一维前缀和
分析
方法1:暴力解法
方法2:前缀和(简单的动态规划)
第一步:预处理
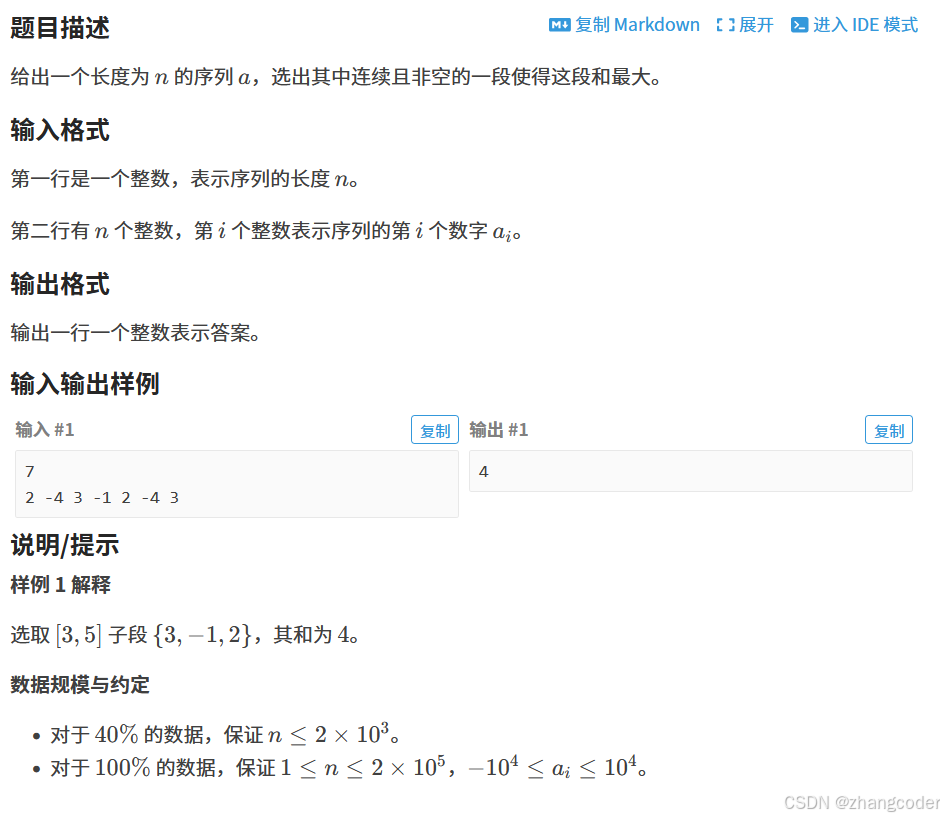
4.练习:P1115 最大子段和
分析
方法1:段长从1枚举到n
方法2:改进方法1
代码
提交结果
1.定义
快速求出数组中某一段的区间和,时间复杂度为(速度极快)
2.作用
可在暴力枚举的过程中快速给出查询的结果,用空间替换时间,从而优化时间复杂度
3.例题:【模板】一维前缀和
https://ac.nowcoder.com/acm/problem/226282
分析
注意到数组从下标为1位置开始计数,原因见之后的算法推导
方法1:暴力解法
直接的想法:先用arr[]存读到的数,读到l和r时就按部就班地计算arr[l]+arr[l+1]+...+arr[r]
注意使用long long存储求和的结果,用int可能会溢出
#include <iostream>
#define endl "\n"
using namespace std;
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n,q,l,r;const long long N=1e5+10; long long arr[N];cin>>n>>q;for (int i=1;i<=n;i++)cin>>arr[i];while(q--){long long sum=0;cin>>l>>r;for (int j=l;j<=r;j++)sum+=arr[j];cout<<sum<<endl; }
}运行结果:运行超时

反思:时间复杂度按最差情况算,如果每次都要计算arr[1]~arr[n]的和,时间复杂度为(q为询问次数
方法2:前缀和(简单的动态规划)
第一步:预处理
预处理一个数组dp[](叫dp的原因是动态规划的英文为dynamic programming,取首字母),其中元素dp[i]表示arr[1]+...+arr[i]的求和结果(即闭区间[1,i]中所有元素的和)
使用递推公式dp[i]=dp[i-1]+dp[i]来快速预处理,时间复杂度为,而若每次计算f[i]都有反复计算arr[1]+...+arr[i],时间复杂度为
★则arr[l]+...+arr[r]等于dp[r]-dp[l-1]
设计代码时,在读arr[i]时就可以预处理前缀和数组
即如果用b表示数组的前n项和,其中
,那么有
(n>=2)(这个就是状态转移方程,等价表示为dp[i]=dp[i-1]+arr[i]),可以使用数组dp[N]来存储所有的
(1<=i<=n)
#include <iostream>
#define endl "\n"
using namespace std;
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n,q,l,r;const long long N=1e5+10; long long arr[N];long long dp[N];cin>>n>>q;cin>>arr[1];//注意从下标为1开始计数dp[1]=arr[1];for (int i=2;i<=n;i++){//一边读arr[i],一边写入dp数组cin>>arr[i];dp[i]=dp[i-1]+arr[i];}while(q--){cin>>l>>r;cout<<dp[r]-dp[l-1]<<endl; }
}(注意从下标从1开始计数,这样好处理,从0开始容易越界访问,例如[0,2]区间的元素的和:dp[2]-dp[-1],-1越界了,设置dp[0]=0,不干扰计算结果)
若i从1开始循环,前缀和计算代码也可以这样写:
dp[0]=0;cin>>n;for (int i=1;i<=n;i++){cin>>arr[i];//i==1时,dp[i-1]==dp[0]dp[i]=dp[i-1]+arr[i];}运行结果:
4.练习:P1115 最大子段和
https://www.luogu.com.cn/problem/P1115
分析
读题可知:"使得这段和最大"应该使用前缀和算法
方法1:段长从1枚举到n
#include <iostream>
#include <climits>
#define endl "\n"
using namespace std;
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n;const long long N=2e5+10; long long arr[N];long long dp[N];long long max=LLONG_MIN; cin>>n;cin>>arr[1];dp[1]=arr[1];for (int i=2;i<=n;i++){cin>>arr[i];dp[i]=dp[i-1]+arr[i];}for (int len=1;len<=n;len++)//段长从1枚举到n{for (int index=1;index+len-1<=n;index++){long long sub=dp[index+len-1]-dp[index-1];if (sub>max)max=sub;}} cout<<max;
}注:long long的最小值的宏为LLONG_MIN,定义在头文件<climits>中
运行结果:超时,算法需要改进,两层for循环时间复杂度过高

方法2:改进方法1
算法:
设数组arr存储读入的n个元素,求以元素arr[i]为结尾的最大子段的和,可以画图演示计算方法

则以元素arr[i]为结尾的子段的和为dp[i]-dp[x],如果要求子段和最大,那么有:
(注:设i为常数)
定义为ret,
为prevmin,显然,求最大使用max函数,求最小使用min函数
暂时写为:
ret=max(?,ret);
prevmin=min(?,prevmin);填补?处:
由于i从1开始因此一开始ret==max(dp[1]-prevmin,ret)==dp[1],那么prevmin的初始值为0(max(dp[1]-prevmin,ret)为max(dp[1],ret)),则可以写出:
ret=max(dp[i]-prevmin,ret);
prevmin=min(dp[i],prevmin);代码
#include <iostream>
#include <algorithm>
#define endl "\n"
using namespace std;
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n,tmp;long long dp[200005];long long prevmin=0,ret=-1e5-10;//ret初始化为负无穷大 cin>>n;dp[0]=0;for (int i=1;i<=n;i++){cin>>tmp;dp[i]=dp[i-1]+tmp;//arr数组可以省略,下面没有用到 }for (int i=1;i<=n;i++) {ret=max(dp[i]-prevmin,ret);prevmin=min(prevmin,dp[i]);}cout<<ret;
}提交结果

相关文章:

CC53.【C++ Cont】一维前缀和
目录 1.定义 2.作用 3.例题:【模板】一维前缀和 分析 方法1:暴力解法 方法2:前缀和(简单的动态规划) 第一步:预处理 4.练习:P1115 最大子段和 分析 方法1:段长从1枚举到n 方法2:改进方法1 代码 提交结果 1.定义 快速求出数组中某一段的区间和,时间复杂度为(速度极…...

Python爬虫实战:研究Grab 框架相关技术
1. 引言 1.1 研究背景与意义 随着互联网的快速发展,网络上的数据量呈爆炸式增长。如何高效地获取和利用这些数据成为了当前的研究热点。网络爬虫作为一种自动获取网页内容的技术,能够按照一定的规则,自动地抓取万维网信息,在搜索引擎、数据挖掘、信息整合等领域有着广泛的…...

每日leetcode
1502. 判断能否形成等差数列 - 力扣(LeetCode) 题目 给你一个数字数组 arr 。 如果一个数列中,任意相邻两项的差总等于同一个常数,那么这个数列就称为 等差数列 。 如果可以重新排列数组形成等差数列,请返回 true …...

YouTube视频字幕转成文章算重复内容吗?
很多创作者误以为「自己说的话不算抄袭」,却不知道YouTube自动生成的字幕早已被搜索引擎存档。 去年就有案例:某美食博主将教程视频字幕转为图文,结果原创度检测仅42%,导致页面权重暴跌。 本文揭秘5个实操技巧:从删除…...

网络学习-利用reactor实现http请求(六)
一、实现HTTP请求 1、印象里面,总有人说C/C语言不能实现HTTP请求,其实不然。C/C语言完全可以实现HTTP请求。通过对select,poll,epoll等IO多路复用技术的学习以及reactor模式的学习,完全能够实现HTTP请求。 2、webserver 主要解决两个问题 …...
)
云原生安全:IaaS安全全解析(从基础到实践)
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念:IaaS的核心价值与安全边界 1.1 什么是IaaS? 基础设施即服务(Infrastructure as a Service)是云计算的基础层,提供虚拟机、存储、网络等基础资源。用户通过…...

【IC_Design】跨时钟域的寄存器更新后锁存
目录 设计逻辑框图场景概述总结电路使用注意事项***波形图代码 设计逻辑框图 场景概述 最典型的应用场景就是——在一个时钟域(比如 CPU/总线域)更新了一个多位配置字,需要把它安全地送到另一个时钟域(比如时钟发生器、串口、视频…...

Spring AI 之提示词
提示词(Prompts)是引导人工智能(AI)模型生成特定输出的输入内容。这些提示词的设计和措辞会显著影响模型的响应。 在 Spring AI 中,与 AI 模型进行交互的最低层级上,处理提示词的方式与 Spring MVC 中管理“视图”(View)有些相似。这涉及创建包含动态内容占位符的冗长…...

亚远景-汽车软件开发的“升级之路”:ASPICE各等级说明
ASPICE(Automotive SPICE)将汽车软件开发过程的成熟度划分为六个等级,从0级到5级,每个等级代表了组织在软件开发过程中的不同能力水平。以下是各等级的详细说明: 等级0:不完整(Incomplete&#…...

Java微服务架构:Spring Cloud全栈指南,附最新Demo源码,可独立运行!
在日常java开发中你是不是经常遇到这种问题:开发中不知道要引入什么版本,创建新项目时直接从老工程拷贝引入了一堆杂乱的包,随便升级下其中一个包就导致整个微服务跑不起来! 如果你也遇到这种问题,可以认证看下本篇文…...
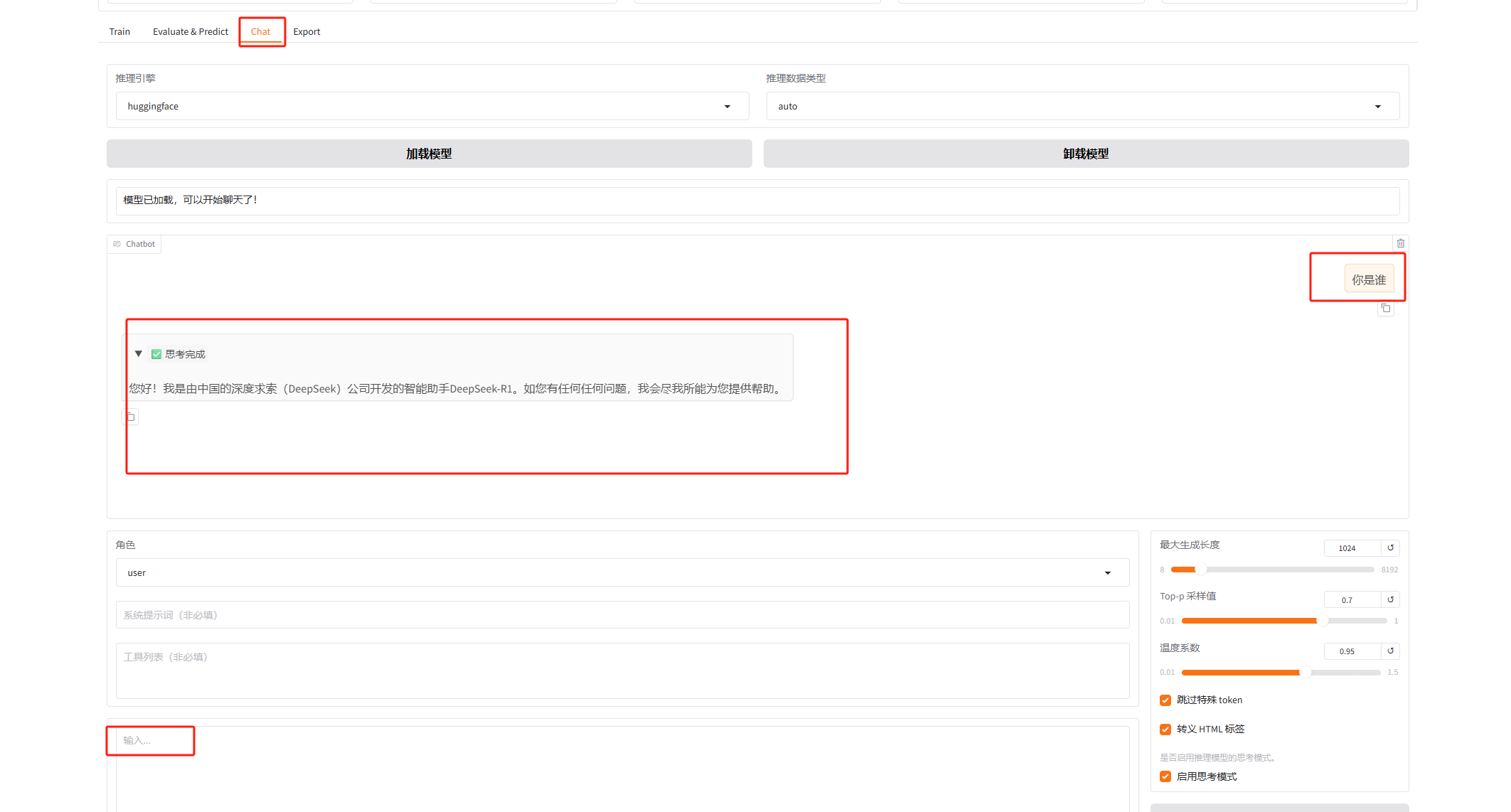
使用LLaMA-Factory微调ollama中的大模型(一)------家用电脑安装LLaMA-Factory工具
前提:本机已安装python,且版本大于3.9,推荐3.10 官方规定如下 我已安装 1.安装torch 查看自己电脑显卡信息 说明我没有装CUDA 使用 nvidia-smi 命令查看驱动信息 说明我NVIDIA 显卡已安装驱动,支持的 CUDA Runtime 版本为 12.6…...
支持向量机(SVM):分类与回归的数学之美
在机器学习的世界里,支持向量机(Support Vector Machine,简称 SVM)是一种极具魅力且应用广泛的算法。它不仅能有效解决分类问题,在回归任务中也有着出色的表现。下面,就让我们深入探索 SVM 如何在分类和回归…...

手撕I2C和SPI协议实现
手撕I2C和SPI协议实现 目录 I2C协议原理I2C位操作实现I2C驱动代码编写SPI协议原理SPI位操作实现SPI驱动代码编写 I2C协议原理 I2C(Inter-Integrated Circuit)是一种串行通信总线,使用两根线:SCL(时钟线)…...

人工智能+:职业价值的重构与技能升级
当“人工智能”成为产业升级的标配时,一个令人振奋的就业图景正在展开——不是简单的岗位替代,而是职业价值的重新定义。这场变革的核心在于,AI并非抢走工作机会,而是创造了人类与技术协作的全新工作范式。理解这一范式转换的逻辑…...

JVM部分内容
1.JVM内存区域划分 为什么要划分内存区域,JAVA虚拟机是仿照真实的操作系统进行设计的,JVM也就仿照了它的情况,进行了区域划分的设计。 JAVA进程也就是JAVA虚拟机会从操作系统申请内存空间给进程使用,JVM内存空间划分,…...

paddlehub搭建ocr服务
搭建环境: Ubuntu20.041080Ti显卡 由于GPU硬件比较老,是Pascal架构,只能支持到paddle2.4.2版本,更高版本无法支持;同时,因为paddle老版本的依赖发生了变化,有些地方存在冲突,花费了…...

python-leetcode 68.有效的括号
题目: 给定一个只包括“(”),{,},[,] 的字符串 s ,判断字符串是否有效。 有效字符串需满足:左括号必须用相同类型的右括号闭合;左括号必须以正确的顺序闭合,…...

人性的裂痕:社会工程学如何成为网络安全的隐形战场
引言 在技术高度发达的今天,网络安全防护墙看似坚不可摧,但黑客却总能找到一条“捷径”——利用人性的弱点。这种被称为“社会工程学”的攻击手段,不依赖复杂的代码漏洞,而是通过心理操纵和信息欺骗,让受害者主动交出…...

ObservableCollection序列化,和监听链表内元素变化
1.ObservableCollection序列化 情景:定义了A类、B类; A类里面有ObservableCollection<B>类型的属性,假设这个属性名称为BList; ObservableCollection<MotionIntervalSegmentation> motionIntervalSegmentation; [B…...

NLP学习路线图(四):Python编程语言
引言 自然语言处理(Natural Language Processing, NLP)是人工智能领域最引人注目的分支之一。从智能客服到机器翻译,从舆情分析到聊天机器人,NLP技术正在重塑人机交互的边界。本文将结合Python编程语言,带您走进NLP的…...

matlab实现无线通信组
无线通信组网涉及多个节点之间的通信,通常需要考虑节点的布局、信号传输、路径损耗、干扰等问题。在MATLAB中,可以通过模拟节点的位置、信号强度、路径损耗等因素来实现一个简单的无线通信组网程序。 1. 节点布局 首先,我们需要定义网络中的…...

基于单片机的室内采光及可燃气体泄漏报警装置设计
标题:基于单片机的室内采光及可燃气体泄漏报警装置设计 内容:1.摘要 随着人们对室内环境安全和舒适度要求的提高,设计一种能实时监测室内采光和可燃气体泄漏情况并及时报警的装置具有重要意义。本设计基于单片机实现室内采光及可燃气体泄漏报警功能,采用…...

Serverless爬虫架构揭秘:动态IP、冷启动与成本优化
一、问题背景:旧技术的瓶颈 在传统爬虫架构中,我们通常部署任务在本地机器或虚拟机中,搭配定时器调度任务。虽然这种方式简单,但存在以下明显缺陷: 固定IP易被封禁:目标网站如拼多多会通过IP频率监控限制…...
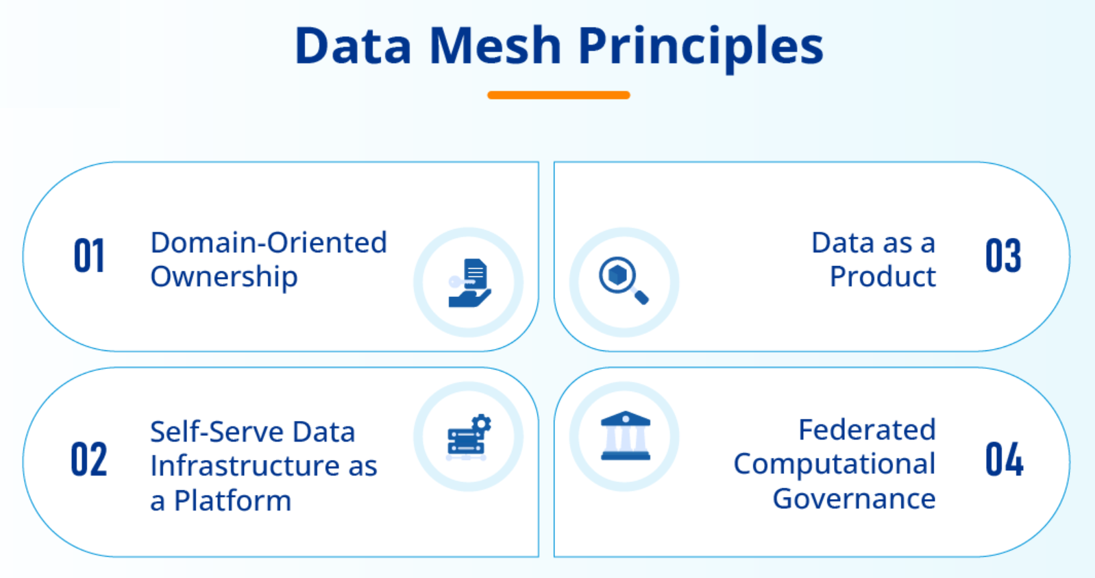
从单体到分布式:深入解析Data Mesh架构及其应用场景与价值
Data Mesh(数据网格)是一种新兴的数据架构范式,旨在解决传统集中式数据平台的可扩展性、敏捷性和治理问题。它强调领域驱动的分布式数据所有权、自助数据平台以及跨组织的协作,使数据成为产品,并通过去中心化的方式提高…...

AI大模型ms-swift框架实战指南(十三):Agent智能体能力构建指南
系列篇章💥 No.文章1AI大模型ms-swift框架实战指南(一):框架基础篇之全景概览2AI大模型ms-swift框架实战指南(二):开发入门之环境准备3AI大模型ms-swift框架实战指南(三)…...

LLM最后怎么输出值 解码语言模型:从权重到概率的奥秘
LM Head Weights(语言模型头部权重):左侧的“LM Head Weights”表示语言模型头部的权重矩阵,它是模型参数的一部分。权重矩阵与输入数据进行运算。Logits(未归一化对数概率):经过与LM Head Weig…...

Leetcode百题斩-回溯
回溯是一个特别经典的问题,也被排在了百题斩的第一部分,那么我们接下来来过一下这个系列。 这个系列一共八道题,偶然间发现我两年前还刷到这个系列的题,回忆起来当时刚经历淘系大变动与jf出走海外事件,大量同事离职闹…...

超小多模态视觉语言模型MiniMind-V 训练
简述 MiniMind-V 是一个超适合初学者的项目,让你用普通电脑就能训一个能看图说话的 AI。训练过程就像教小孩:先准备好图文材料(数据集),教它基础知识(预训练),再教具体技能…...

边缘云的定义、实现与典型应用场景!与传统云计算的区别!
一、什么是边缘云? 边缘云是一种分布式云计算架构,将计算、存储和网络资源部署在靠近数据源或终端用户的网络边缘侧(如基站、本地数据中心或终端设备附近),而非传统的集中式云端数据中心。 核心特征&…...

HarmonyOS 鸿蒙应用开发基础:父组件和子组件的通信方法总结
在鸿蒙开发中,ArkUI声明式UI框架提供了一种现代化、直观的方式来构建用户界面。然而,由于其声明式的特性,父组件与子组件之间的通信方式与传统的命令式框架有所不同。本文旨在详细探讨在ArkUI框架中,父组件和子组件通信的方法总结…...