C++修炼：红黑树的模拟实现

        Hello大家好！很高兴我们又见面啦！给生活添点passion，开始今天的编程之路！

我的博客：<但凡.

我的专栏：《编程之路》、《数据结构与算法之美》、《题海拾贝》、《C++修炼之路》

欢迎点赞，关注！

       

目录

1、红黑树的概念

        1.1、什么是红黑树

        1.2、红黑树和AVL树的对比

        1.3、红黑树复杂度

2、红黑树模拟实现

        2.1、红黑树的结构

2.1、红黑树的插入

        2.1.1、插入情况分析

        一、叔叔存在且为红

        二、叔叔存在且为黑或叔叔不存在，并且新增节点是父亲的左

        三、叔叔存在且为黑或叔叔不存在，并且新增节点是父亲的右

         2.2.2、插入代码实现

2.3、查找

2.4、检查是否为二叉树

2.5、其他

3、红黑树的应用

---

        因为map和set的底层使用红黑树实现的，所以我们先讲解一下红黑树，并模拟实现一下红黑树，为下一期的map和set封装做铺垫。

1、红黑树的概念

        1.1、什么是红黑树

        红黑树是一颗二叉搜索树，他的每个节点都有一个颜色，颜色只能是红色或黑色。和AVL树一样，他也是依靠着几条规则来尽可能保证平衡，保证搜索效率的。我们开门见山直接介绍一下这几条规则：

        （1）每个节点不是红色就是黑色（上面说过了）。

        （2）根节点是黑色的。

        （3）不能出现两个连续的红色节点（如果父亲是红色，孩子一定不是红色）。

        （4）从根节点到任意一个NULL空节点的路线上所含有的黑色节点数量相等。

        当然由于红黑树是一颗二叉搜索树，所以他也具有二叉搜索树的特点。

        基于以上四点规则，红黑树能保证从根节点到NULL节点的最长路径不会超过最短路径的两倍。

        我先给大家透露一点，红黑树也是通过各种旋转来保证平衡，只不过是他不再依靠平衡因子了，而是依靠颜色。红黑树的平衡性没有AVL那么极致，这意味着插入同样的节点构建一棵红黑树需要的旋转次数更少。

        一棵红黑树：

         1.2、红黑树和AVL树的对比

         有些区别我们说过了，我们说一下为什么红黑树的查找比AVL树稍慢。

        其实核心原因还是因为红黑树的树高可能会比AVL树高，因为他不是严格控制平衡。由于搜索（查找）只能是从头到尾遍历这颗树，如果树高更高的话，不可避免的搜索路径更长，效率更低。

        对于100万个节点的树，AVL树高度约20层，而 红黑树高度最多约四十层。

       1.3、红黑树复杂度

         空间复杂度：O(N)，时间复杂度：插入，查找，删除都是O(logN)。

2、红黑树模拟实现

         又到了经典的模拟实现环节哈哈。

        2.1、红黑树的结构

enum Colour
{RED,BLACK
};
template<class K,class V>
struct RBTreeNode
{pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Colour _col;RBTreeNode(const pair<K,V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED){}
};
template<class K,class V>
class RETree
{typedef RBTreeNode<K, V> Node;
public:private:Node* _root = nullptr;
};

         和AVL树的节点类似，只不过是把平衡因子换成了颜色标记。另外就是我们这里实现的红黑树默认是key_value类型的，为的是方便后面map的封装（没错，set也是用的key_value版本的红黑树）。但是所有的比较都是按照key来比较的。

2.1、红黑树的插入

         红黑树的插入可以说是最最核心的部分了，所以说我们先分析一下再模拟实现。

        2.1.1、插入情况分析

        插入情况有三种，我们这三种情况的区分是按照叔叔（父亲的兄弟节点）的颜色和是否存在，以及父亲节点和新增节点的位置关系进行区分的。其实严格来讲有六种，因为父亲有可能是爷爷的左，也可能是爷爷的右，但是前三种和后三种其实是非常类似的，只是方向换了一下。

        首先我要说明一点，我们所有的新增节点默认都是红色的，因为对于新插入的节点，如果是红色节点他破坏的是规则三，如果插入的是黑色节点，破坏的是规则四，很显然规则四比规则三更难调整。

        一、叔叔存在且为红

        这是最简单的一种情况，只变色不旋转。

  

         当父亲是爷爷的左的时候情况一样，就是单纯变色，不画图了。

         二、叔叔存在且为黑或叔叔不存在，并且新增节点是父亲的左

        当父亲节点是爷爷节点的左，这种情况是单旋加变色：

  

         （我拿最简单的情况来做说明了）

          在上面这种情况下，我们先对爷爷就行右旋，然后再进行变色，把父亲变成黑色，爷爷变成红色。

        和他类似的，当父亲节点是爷爷的右子树，进行如下操作：

  

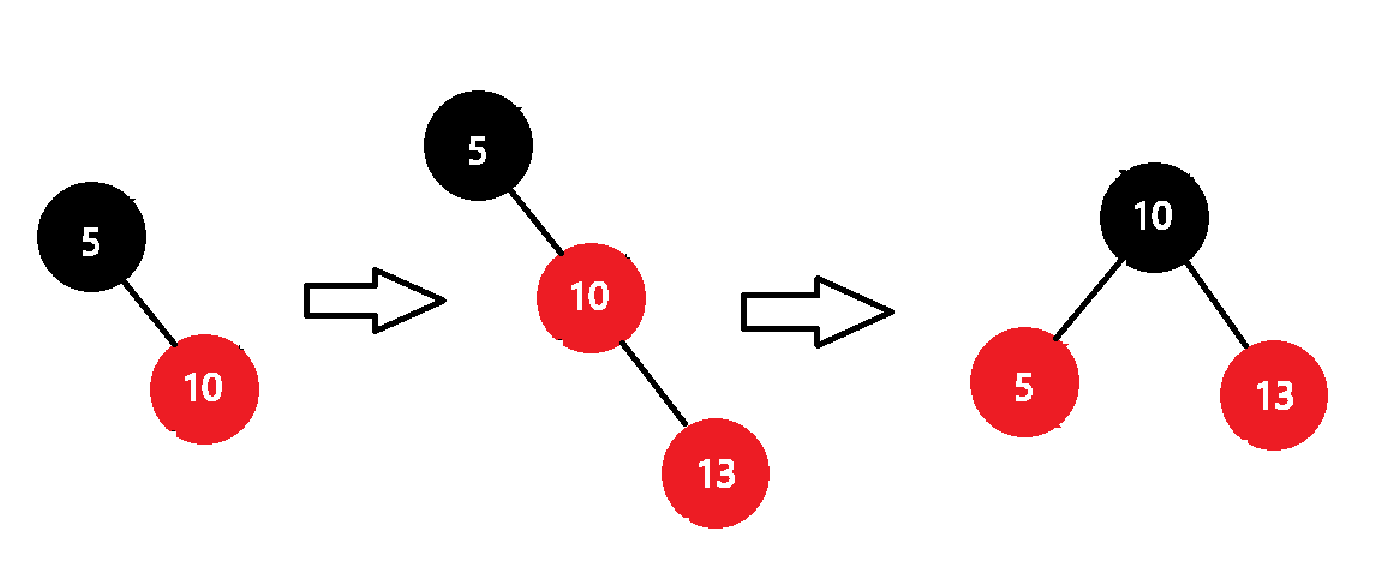
        三、叔叔存在且为黑或叔叔不存在，并且新增节点是父亲的右

        首先第一种情况是父亲是爷爷的左：

        如果父亲是爷爷的右： 

  

        写到这里大家也应该发现了，我们旋转的情况和AVL树是一样的，如果是单纯的一边高，我们就单旋，如果是左子树的右子树高或者右子树的左子树高，也就是不是单纯一边高的，就进行双旋。除此之外的不同就是我们把平衡因子的调整换成了颜色的调整。

        好了以上就是红黑树插入调整的大概几种情形，当然还有叔叔存在且为黑的情况我没画图，因为在代码实现上，叔叔存在且为黑和叔叔不存在属于一种情况，所以说就不画图了（其实是我很懒）。

        接下来我们梳理一下这几种情况：

一、如果父亲是爷爷的左节点

        （1）如果叔叔存在且为红

                       单纯调色

        （2）如果叔叔不存在或叔叔存在且为黑

                        1、如果新增节点是父亲的左

                                单旋加变色。

                        2、如果新增节点是父亲的右

                                双旋加变色。

二、如果父亲是爷爷的右节点

        （1）如果叔叔存在且为红

                       单纯调色

        （2）如果叔叔不存在或叔叔存在且为黑

                        1、如果新增节点是父亲的右

                                单旋加变色。

                        2、如果新增节点是父亲的左

                                双旋加变色。

         2.2.2、插入代码实现

bool Insert(const pair<K, V>& kv)
{//如果树为空就把这个节点作为根if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;//默认为黑return true;}//查找插入位置Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;//不允许重复值}}//新插入红色节点cur = new Node(kv);cur->_col = RED;//讲解//先插入再调整if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;//叔叔存在且为红if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//循环向上处理cur = grandfather;//此时爷爷相当于是新增红节点parent = cur->_parent;}else//叔叔不存在或叔叔存在且为黑{if (cur == parent->_left){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{RotateL(parent);RatateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){RatateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}//都更改完后需要调整根节点的颜色，因为根节点颜色可能被改变了_root->_col = BLACK;
}

        如果父亲存在并且父亲的颜色为红，说明此时有两个连续的红，我们就进行调整。这里说一点为什么循环条件中没有判断爷爷是否存在。首先我们设想爷爷不存在的场景，即父亲是根节点。此时爷爷的确不存在，但是由于父亲的颜色一定是黑色的（在此之前我们无法破坏这一点规则），所以说循环一定进不去。也就不必判断爷爷是否存在了。

        还有一个特别特别需要注意的点，如果我们是旋转调整（即第二三中情况），在调整完之后直接退出循环，因为此时我们的爷爷是黑色的，而在第一种情况的变色下爷爷是红色的，如果爷爷是黑色不会破坏规则四，就不要继续循环了。

        以下是两种旋转的代码，和之前AVL树的旋转完全一样，不作解释了直接放在这里：

void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppnode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppnode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subR;}else{ppnode->_right = subR;}subR->_parent = ppnode;}}

2.3、查找

        和之前树的查找一样，不多说了。

Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if (cur->_kv.first > key){cur = cur->_left;}else{return cur;}}return nullptr;}

 2.4、检查是否为二叉树

        这个检查不是重点，不做讲解。

bool Check(Node* root, int blackNum, const int refNum){if (root == nullptr){// 前序遍历走到空时，意味着一条路径走完了if (blackNum != refNum){cout << "存在黑色结点的数量不相等的路径" << endl;return false;}return true;}// 检查孩子不太方便，因为孩子有两个，且不一定存在，反过来检查父亲就方便多了if (root->_col == RED && root->_parent->_col == RED){cout << root->_kv.first << "存在连续的红色结点" << endl;return false;}if (root->_col == BLACK){++blackNum;}return Check(root->_left, blackNum, refNum) && Check(root->_right, blackNum, refNum);}bool IsBalanceTree(){if (_root == nullptr)return true;if (_root->_col == RED)return false;// 参考值int refNum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++refNum;}cur = cur->_left;}return Check(_root, 0, refNum);}

 2.5、其他

        以下是二叉树节点数，二叉树高度，二叉树先序遍历的代码，很早之前在数据结构篇的二叉树部分就说过了，不做解析。

int _Size(Node* root){return root == nullptr ? 0 :_Size(root->_left) + _Size(root->_right) + 1;}int _Height(Node* root){if (root == nullptr)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}

3、红黑树的应用

1. C++ STL中的map和set：通常使用红黑树实现（下一期就是map和set模拟实现）

2. Linux内核：进程调度、内存管理等

3. 数据库系统：索引结构

4. 实时系统：需要保证最坏情况下性能的场景

        好了，今天的内容就分享到这，我们下期再见！