从逻辑视角学习信息论:概念框架与实践指南

文章目录
- 一、信息论的逻辑基础与哲学内涵
- 1.1 信息的逻辑本质:区分与差异
- 1.2 逆范围原理与信息内容
- 二、信息论与逻辑学的概念交汇
- 2.1 熵作为逻辑不确定性的度量
- 2.2 互信息与逻辑依赖
- 2.3 信道容量的逻辑极限
- 三、信息论的核心原理与逻辑基础
- 3.1 最大熵原理的逻辑正当性
- 3.2 编码理论的逻辑结构
- 3.3 信息论推理的逻辑框架
- 四、技术细节与实用工具
- 4.1 压缩算法的逻辑实现
- 4.2 错误纠正的逻辑原理
- 4.3 信息论软件工具
- 五、信息论在现代科技中的逻辑应用
- 5.1 机器学习中的信息论原理
- 5.2 信息瓶颈理论的深度学习启示
- 5.3 量子信息的逻辑扩展
- 六、从逻辑学家视角的学习路径
- 6.1 基础准备与概念建立
- 6.2 核心学习序列
- 6.3 常见挑战与解决方案
- 七、信息论的跨学科整合与未来展望
- 7.1 与数据科学的深度融合
- 7.2 人工智能的信息论视角
- 7.3 跨学科应用前景
- 结论:逻辑学家的信息论之旅
这一篇博客的续篇:从逻辑学视角严谨证明数据加密的数学方法与实践
一、信息论的逻辑基础与哲学内涵
1.1 信息的逻辑本质:区分与差异
信息论的逻辑基础远超其数学表达,根植于对信息、不确定性和推理本质的深刻理解。David Ellerman的逻辑熵理论为信息论提供了严格的逻辑基础,他认为信息本质上关乎"区分、差异、可区分性和多样性"。
逻辑熵原理:信息通过逻辑熵来度量——即两次独立试验产生区别的概率。这提供了一个基于分区所做区分的预概率信息概念。
逻辑信息论是"分区逻辑的定量版本,正如逻辑概率论是对偶布尔子集逻辑的定量版本"。这种理解将信息直接与逻辑结构联系起来,使逻辑学家能够从熟悉的概念框架出发理解信息论。
1.2 逆范围原理与信息内容
Bar-Hillel和Carnap建立的逻辑信息方法始于逆范围原理:
- 命题携带的信息越多,其为真的可能性越小
- 信息内容与支持命题的可能性范围成反比
- 这将信息直接连接到逻辑概率和可能世界语义
信息作为范围缩减的概念框架特别适合逻辑学家理解:
- 获得信息前:可能状态或世界的范围保持开放
- 获得信息后:范围缩小,减少关于实际配置的不确定性
- 逻辑推论:信息流遵循可能性消除的逻辑模式
认识论意义:Dretske的工作表明,知识发生在信息因果流动产生合理信念时,这为知识论提供了自然主义基础。
二、信息论与逻辑学的概念交汇
2.1 熵作为逻辑不确定性的度量
从逻辑视角理解Shannon熵的核心概念:
熵的逻辑含义:
- 熵代表保持开放的逻辑可能性空间
- 每比特信息消除一半的逻辑可能性
- 最大熵分布代表给定约束下的最大逻辑不确定性状态
这种理解将抽象的数学概念H(X) = -Σp(x)log p(x)转化为直观的逻辑概念——解决系统状态歧义所需的信息量。
2.2 互信息与逻辑依赖
互信息I(X;Y) 在逻辑框架中表示:
- 变量间逻辑依赖程度的量化
- 一个逻辑命题的知识如何影响另一个命题的不确定性
- 零互信息表示逻辑独立
实践启示:在机器学习中,互信息用于特征选择,本质上是寻找与目标变量有最强逻辑关联的特征。
2.3 信道容量的逻辑极限
信道容量C代表可靠传输的最大逻辑信息量。Shannon-Hartley定理C = W log₂(1 + SNR)从逻辑角度表明:
- 存在信息传输的基本物理和逻辑约束
- 错误纠正通过逻辑冗余实现
- 最优编码反映信息源的逻辑结构
三、信息论的核心原理与逻辑基础
3.1 最大熵原理的逻辑正当性
最大熵原理从逻辑角度具有深刻意义:
认识论谦逊:最大熵代表给定约束下的最大无知
客观推理:提供最少偏见的概率分配
一致性保证:确保跨不同推理方法的一致概率分配
Jaynes的洞见:“最大熵原理是唯一在所有情况下都能给出一致结果的方法。”
3.2 编码理论的逻辑结构
从逻辑视角理解编码原理:
Huffman编码:
- 频繁符号获得短码的逻辑:减少平均传输信息量
- 前缀自由性质的逻辑必要性:确保唯一可解码性
算法信息论(Kolmogorov复杂度):
- 信息内容定义为产生字符串的最短程序长度
- 随机字符串具有最大信息内容的逻辑
- 最小描述长度原理:Ockham剃刀的信息论形式化
3.3 信息论推理的逻辑框架
最小描述长度(MDL)推理:
- 选择最小化数据描述长度的模型
- 逻辑简单性:更简单的理论需要更短的描述
- 预测能力:更好的压缩意味着更好的预测
这种方法提供了归纳推理的通用框架,将逻辑简单性与预测准确性统一起来。
四、技术细节与实用工具
4.1 压缩算法的逻辑实现
算术编码vs Huffman编码:
- Huffman:符号级编码,实现简单但受整数码长限制
- 算术编码:消息级编码,可接近熵极限,体现了"整体大于部分之和"的逻辑
实际应用中的逻辑权衡:
- 压缩率vs计算复杂度
- 实时性vs最优性
- 错误传播vs压缩效率
4.2 错误纠正的逻辑原理
Reed-Solomon码:
- 基于有限域上的多项式插值
- 可纠正多个符号错误,体现了冗余的逻辑价值
- CD/DVD应用:即使有划痕也能正常播放
Turbo码和LDPC码:
- 迭代解码体现了逻辑推理的迭代细化过程
- 接近Shannon极限,证明了理论界限的可达性
深空通信案例:Voyager任务使用的纠错码使得跨越数十亿英里的通信成为可能,展示了信息论设计原则的威力。
4.3 信息论软件工具
PyPhi(集成信息论):
- 分析因果结构的数学框架
- 应用于神经科学、意识研究
- 体现了信息论在复杂系统分析中的应用
信息论工具箱:
- ITIP:自动证明信息论不等式
- 神经科学信息论工具箱:分析神经数据
- 展示了信息论作为通用分析框架的价值
五、信息论在现代科技中的逻辑应用
5.1 机器学习中的信息论原理
KL散度在深度学习中的核心地位:
- 作为优化目标度量分布差异
- VAE中的正则化项
- 强化学习中的策略优化
交叉熵损失的逻辑解释:
- 使用错误分布编码真实分布的预期比特数
- 最小化交叉熵等价于最大化似然
- 连接了信息论与统计推断
5.2 信息瓶颈理论的深度学习启示
理论框架:
- 寻找输入X的压缩表示T,保留关于目标Y的相关信息
- 权衡:压缩(最小化I(X;T))vs 相关性(最大化I(T;Y))
神经网络的信息论理解:
- 深层网络通过信息瓶颈学习
- 解释了深度学习的泛化能力
- 指导网络架构设计
实践意义:信息瓶颈原理帮助设计更高效的神经网络架构,减少过拟合。
5.3 量子信息的逻辑扩展
量子纠缠的信息论刻画:
- 经典信息论无法完全描述量子关联
- 量子熵和纠缠熵提供新的度量
- 量子信道容量超越经典极限
量子密钥分发(QKD):
- 安全性由物理定律而非计算假设保证
- BB84协议体现了量子测量的信息论特性
- 商用QKD设备已经实现
六、从逻辑学家视角的学习路径
6.1 基础准备与概念建立
必要的数学基础:
- 概率论:离散和连续概率,条件概率,贝叶斯定理
- 离散数学:组合数学,图论基础
- 分析基础:对数函数,基本微积分
概念优先于计算:
- 先理解信息度量代表什么,再深入计算细节
- 使用熟悉的逻辑概念(蕴含、推理)解释信息论思想
- 通过实现简单编码方案建立直觉
6.2 核心学习序列
第一阶段:基础概念(2-3周)
- Shannon的原始框架和动机
- 熵和基本信息度量
- 通过具体例子建立直觉
第二阶段:编码理论(3-4周)
- 源编码定理和压缩算法
- 信道编码和纠错码
- 理论极限与实际实现
第三阶段:高级应用(4-5周)
- 与统计推断的联系
- 机器学习中的应用
- 现代发展方向
学习建议:MacKay的《信息论、推理与学习算法》特别适合计算机科学背景的学习者,它成功连接了理论与应用。
6.3 常见挑战与解决方案
概率基础薄弱:
- 从离散概率开始,逐步过渡到连续情况
- 大量练习条件概率和贝叶斯推理
直觉vs形式化:
- 平衡数学严格性与概念理解
- 使用可视化和模拟辅助理解
信息vs意义:
- 明确区分Shannon的技术定义与日常含义
- 理解信息论处理的是语法而非语义
七、信息论的跨学科整合与未来展望
7.1 与数据科学的深度融合
现代数据科学的信息论基础:
- 特征选择:最大化互信息
- 降维:保留最大信息量
- 聚类:最小化类内信息散度
大数据时代的新挑战:
- 分布式信息处理
- 隐私保护的信息论方法
- 因果推断的信息论框架
7.2 人工智能的信息论视角
深度学习的信息论理解:
- 网络深度与信息处理能力
- 注意力机制的信息论解释
- 生成模型的信息论基础
未来研究方向:
- 可解释AI的信息论方法
- 强化学习的信息论优化
- 神经网络压缩的理论界限
前沿洞察:信息论正在成为理解和设计智能系统的核心理论框架。
7.3 跨学科应用前景
计算生物学:
- 基因组信息分析
- 蛋白质折叠的信息论模型
- 进化的信息论理解
认知科学:
- 意识的集成信息论
- 感知的信息论模型
- 学习和记忆的信息处理
复杂系统:
- 网络信息流分析
- 涌现现象的信息论刻画
- 系统韧性的信息论度量
结论:逻辑学家的信息论之旅
从逻辑视角学习信息论,我们发现这不仅是一套数学工具,更是理解信息、知识和推理本质的概念框架。对逻辑学家而言,信息论提供了:
- 量化不确定性的工具——补充定性逻辑方法
- 连接离散与连续的桥梁——对现代AI至关重要
- 从理论到应用的完整体系——跨越计算机科学各个领域
- 深刻的哲学洞见——关于知识、信息和现实的本质
信息论的学习之旅,是从Shannon的实用通信问题出发,最终触及关于现实逻辑结构的深刻问题。这种从数学抽象到哲学洞察的转变,展示了数学工具如何转化我们对基本哲学概念的理解,同时保持严格的逻辑基础。
在信息时代,掌握信息论不仅是技术需要,更是理解和塑造数字世界的关键。对逻辑学家而言,这是一次将形式推理能力扩展到定量领域的绝佳机会,为解决现代计算挑战提供坚实的理论基础。
相关文章:

从逻辑视角学习信息论:概念框架与实践指南
文章目录 一、信息论的逻辑基础与哲学内涵1.1 信息的逻辑本质:区分与差异1.2 逆范围原理与信息内容 二、信息论与逻辑学的概念交汇2.1 熵作为逻辑不确定性的度量2.2 互信息与逻辑依赖2.3 信道容量的逻辑极限 三、信息论的核心原理与逻辑基础3.1 最大熵原理的逻辑正当…...

springboot配置mysql druid连接池,以及连接池参数解释
文章目录 前置配置方式参数解释 前置 springboot 项目javamysqldruid 连接池 配置方式 在 springboot 的 application.yml 中配置基本方式 # Druid 配置(Spring Boot YAML 格式) spring:datasource:url: jdbc:mysql://localhost:3306/testdb?useSSL…...

Spring Boot集成Resilience4j实现微服务容错机制
在Spring Boot中集成Resilience4j实现微服务容错 引言 在微服务架构中,服务之间的调用不可避免,但由于网络延迟、服务不可用等问题,调用失败的情况时有发生。为了提高系统的稳定性和可用性,我们需要引入容错机制。Resilience4j是…...
 本地hadoop虚拟机系统设置)
(一) 本地hadoop虚拟机系统设置
1.配置固定IP地址(每一台都配置) 开启node1,修改主机名为node1,并修改固定IP为:192.168.88.131 # 修改主机名 hostnamectl set-hostname node1# 修改IP vim /etc/sysconfig/network-scripts/ifcfg-ens33 IPADDR"…...

TDengine 运维—容量规划
概述 若计划使用 TDengine 搭建一个时序数据平台,须提前对计算资源、存储资源和网络资源进行详细规划,以确保满足业务场景的需求。通常 TDengine 会运行多个进程,包括 taosd、taosadapter、taoskeeper、taos-explorer 和 taosx。 在这些进程…...

【MySQL成神之路】MySQL索引相关介绍
1 相关理论介绍 一、索引基础概念 二、索引类型 1. 按数据结构分类 2. 按功能分类 三、索引数据结构原理 B树索引特点: 哈希索引特点: 四、索引使用原则 1. 创建索引原则 2. 避免索引失效情况 五、索引优化策略 六、索引维护与管理 七、特殊…...

PPP 拨号失败:ATD*99***1# ... failed
从日志来看,主要有两类问题: 一、led_indicator_stop 报 invalid p_handle E (5750) led_indicator: …/led_indicator.c:461 (led_indicator_stop):invalid p_handle原因分析 led_indicator_stop() 的参数 p_handle (即之前 led_indicator…...

PostgreSQL跨数据库表字段值复制实战经验分
场景需求 在实际工作中,我们经常需要将一个PostgreSQL数据库中的表字段值复制到另一个数据库中。最近我在处理两个ERP系统数据库(A库和B库)之间的数据同步时,就遇到了这样的需求:需要将B库中sale_order表的合同信息&a…...
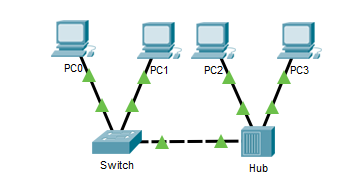
【计网】五六章习题测试
目录 1. (单选题, 3 分)某个网络所分配到的地址块为172.16.0.0/29,能接收目的地址为172.16.0.7的IP分组的最大主机数是( )。 2. (单选题, 3 分)若将某个“/19”的CIDR地址块划分为7个子块,则可能的最小子块中的可分配IP地址数量…...
汇川EasyPLC MODBUS-RTU通信配置和编程实现
累积流量计算(MODBUS RTU通信数据处理)数据处理相关内容。 累积流量计算(MODBUS RTU通信数据处理)_流量积算仪modbus rtu通讯-CSDN博客文章浏览阅读219次。1、常用通信数据处理MODBUS通信系列之数据处理_modbus模拟的数据变化后会在原来的基础上累加是为什么-CSDN博客MODBUS通…...

从 CANopen到 PROFINET:网关助力物流中心实现复杂的自动化升级
使用 CANopen PLC 扩展改造物流中心的传送带 倍讯科技profinet转CANopen网关BX-601-EIP将新的 PROFINET PLC 系统与旧的基于 CANopen 的传送带连接起来,简化了物流中心的自动化升级。 新建还是升级?这些问题通常出现在复杂的内部物流设施中,…...

基于Yolov8+PyQT的老人摔倒识别系统源码
概述 基于Yolov8PyQT的老人摔倒识别系统,该系统通过深度学习算法实时检测人体姿态,精准识别站立、摔倒中等3种状态,为家庭或养老机构提供及时预警功能。 主要内容 完整可运行代码 项目采用Yolov8目标检测框架结合PyQT5开发…...

wsl2 不能联网
wsl2 安装后用 wifi 共享是能联网,问题出在公司网络限制 wsl2 IP 访问网络,但是主机可以上网。 解决办法,在主机用 nginx 设置代理,可能需要开端口权限 server {listen 9000;server_name localhost;location /ubuntu/ {#…...

双击重复请求的方法
1、限制点击次数 2、vue中 可以自定义一个属性指令 preventReClick.js中定义: import Vue from vue Vue.directive(preventReClick, {inserted: (el, binding) > {el.addEventListener(click, () > {if (!el.disabled) {el.disabled truesetTimeout(() >…...

Java[IDEA]里的debug
目录 前言 Debug 使用Debug 总结 前言 这里我说一下就是 java IDEA 工具里的debug工具 里的一个小问题 就是 当我们使用debug去查看内部文档 查看不到 是为什么 Debug 所谓 debug 工具 他就是用来调试程序的 当我们写代码 报错 出错时 我们就可以使用这个工具 因此这个工具…...

一条SQL语句的旅程:解析、优化与执行全过程研究
1、引言 在现代信息系统中,数据库是核心组件之一。SQL(结构化查询语言)作为与数据库交互的主要方式,其执行效率直接影响到整个系统的性能表现。虽然开发者常常只需编写一行简单的 SQL,但数据库内部却经历了一个复杂而精密的过程来完成这条 SQL 的处理。 本文将以一个完整…...

动态规划经典三题_完全平方数
279. 完全平方数 给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。 完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而…...
)
LVGL(lv_textarea文本框控件)
文章目录 一、lv_textarea 是什么?二、基本用法1. 创建 lv_textarea 对象2. 设置提示文字(占位符)3. 设置最大长度4. 设置密码模式(显示为\*号)5. 获取和设置内容6. 配合虚拟键盘使用(常用于触摸屏…...

蓝桥杯国14 互质
问题描述 请计算在 [1,2023的2023次幂] 范围内有多少个整数与 2023 互质。由于结果可能很大,你只需要输出对 1097 取模之后的结果。 答案提交 这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个…...

DAO模式
1. 持久化 简单来说,就是把代码的处理结果转换成需要的格式进行储存。 2. JDBC的封装 3. DAO模式 4. Properties类与Properties配置文件 添加 读取 5. 使用实体类传递数据 6. 总结 附录: BaseDao指南 BaseDao指南-CSDN博客...
ECharts图表工厂,完整代码+思路逻辑
Echart工厂支持柱状图(bar)折线图(line)散点图(scatter)饼图(pie)雷达图(radar)极坐标柱状图(polarBar)和极坐标折线图(po…...

Logback 在 Spring Boot 中的详细配置
1. Logback 配置文件 Spring Boot 默认会加载 classpath 下的 logback-spring.xml(推荐)或 logback.xml 作为 Logback 的配置文件。 推荐使用 logback-spring.xml,因为 Spring Boot 提供了扩展支持(例如基于 Profile 的配置&am…...

写起来比较复杂的深搜题目
年轻的拉尔夫开玩笑地从一个小镇上偷走了一辆车,但他没想到的是那辆车属于警察局,并且车上装有用于发射车子移动路线的装置。 那个装置太旧了,以至于只能发射关于那辆车的移动路线的方向信息。 编写程序,通过使用一张小镇的地图…...

MySQL强化关键_016_存储引擎
目 录 一、概述 二、MySQL 支持的存储引擎 三、指定存储引擎 四、修改存储引擎 五、常用存储引擎及适用场景 一、概述 MySQL 存储引擎决定了数据在磁盘上的存储方式和访问方式;不同的存储引擎实现了不同的存储和检索算法;MySQL 常见的存储引擎&…...

CSS:margin的塌陷与合并问题
文章目录 一、margin塌陷问题二、margin合并问题 一、margin塌陷问题 二、margin合并问题...

防护等级IPxx含义 -雨天充电需要防护盖吗
指标快要到期,新买的电车,第一次碰到雨天充电的问题,有点担心漏电。然后电商平台上一查,果然有卖防护罩的,但是真的需要吗? 下面从充电口防护等级,国标要求、注意事项等几个方面分析。 一、防护…...

【设计模式】责任链+模板+工程模式使用模板
前言 方便写出优雅,解耦,高内聚,高复用的代码。 Demo // 1. 定义验证器接口(责任链模式) public interface Validator {Validator setNext(Validator next);boolean validate(Data data); }// 2. 创建抽象验证器&am…...

探索服务网格(Service Mesh):云原生时代的网络新范式
文章目录 一、引言二、什么是服务网格基本定义形象比喻 三、服务网格解决了哪些问题微服务通信复杂性可观察性安全性 四、常见的服务网格实现IstioLinkerdConsul Connect 五、服务网格的应用场景大型微服务架构混合云环境 六、服务网格的未来发展与其他技术的融合标准化和行业规…...

SQL SERVER中实现类似LEAST函数的功能,返回多列数据中的最小值
使用 LEAST()函数可以简洁地在一行SQL语句中找出多个值中的最小值,但在SQLServer数据库中,没有内置的LEAST函数。 我们可以使用values子句创建临时的数据集的办法,返回多列数据中的最小值。 创建表 CREATE TABLE stu…...

SymPy | 获取表达式自由变量方法与因式分解
SymPy 是 Python 中强大的符号计算库,广泛应用于数学建模、公式推导和科学计算。本文将从两个核心功能展开:表达式中自由变量的获取与因式分解的实现,通过完整代码示例和深入分析,帮助读者掌握其使用方法。 第一部分:获…...
