【深度学习】2. 从梯度推导到优化策略:反向传播与 SGD, Mini SGD
反向传播算法详解
1. 前向传播与输出层误差定义
假设我们考虑一个典型的前馈神经网络,其最后一层为 softmax 分类器,损失函数为交叉熵。
前向传播过程

对于某一隐藏层神经元 j j j:
-
输入: x i x_i xi
-
权重: w j i w_{ji} wji
-
线性组合:
net j = ∑ i w j i x i = w j ⊤ x \text{net}_j = \sum_i w_{ji} x_i = \mathbf{w}_j^\top \mathbf{x} netj=i∑wjixi=wj⊤x -
激活输出:
y j = f ( net j ) y_j = f(\text{net}_j) yj=f(netj)
最终输出层采用 softmax 函数,输出概率:
z k = e net k ∑ k ′ e net k ′ z_k = \frac{e^{\text{net}_k}}{\sum_{k'} e^{\text{net}_{k'}}} zk=∑k′enetk′enetk
训练误差(Training Error)
在训练神经网络时,损失函数(training error)用于衡量预测输出 z \mathbf{z} z 与目标标签 t \mathbf{t} t 之间的距离。常见的损失函数包括以下三种形式:
1. 欧几里得距离(Euclidean distance)
这是最基本的损失函数形式,适用于回归任务或输出不是概率分布时:
J ( t , z ) = 1 2 ∑ k = 1 C ( t k − z k ) 2 = 1 2 ∥ t − z ∥ 2 J(t, z) = \frac{1}{2} \sum_{k=1}^{C} (t_k - z_k)^2 = \frac{1}{2} \| \mathbf{t} - \mathbf{z} \|^2 J(t,z)=21k=1∑C(tk−zk)2=21∥t−z∥2
其中:
- C C C 是输出类别数
- t \mathbf{t} t 是目标向量
- z \mathbf{z} z 是模型输出
它表示的是平方误差损失,数值意义上等价于 L2 范数。
2. 交叉熵(Cross Entropy)
当 t \mathbf{t} t 和 z \mathbf{z} z 都是概率分布(如 one-hot 和 softmax 输出)时,更推荐使用交叉熵损失:
J ( t , z ) = − ∑ k = 1 C t k log z k J(t, z) = - \sum_{k=1}^{C} t_k \log z_k J(t,z)=−k=1∑Ctklogzk
该形式特别适合用于多分类问题,且与 softmax 联合使用可得到简洁的梯度表达式。
3. 对称交叉熵(Symmetric Cross Entropy)
标准交叉熵是非对称的,即 J ( t , z ) ≠ J ( z , t ) J(t, z) \ne J(z, t) J(t,z)=J(z,t)。为了在某些任务中保持对称性,可以使用如下形式:
J ( t , z ) = − ∑ k = 1 C ( t k log z k + z k log t k ) J(t, z) = - \sum_{k=1}^{C} (t_k \log z_k + z_k \log t_k) J(t,z)=−k=1∑C(tklogzk+zklogtk)
这种形式在一些模糊标签、不确定性建模或鲁棒学习中更常见,但需要确保 t k > 0 t_k > 0 tk>0 且 z k > 0 z_k > 0 zk>0,否则 log 项会出现数值问题。
小结
| 损失函数类型 | 应用场景 |
|---|---|
| 欧几里得距离 | 回归或非概率输出 |
| 交叉熵 | 分类任务,概率分布输出(softmax) |
| 对称交叉熵 | 非对称性敏感的分类问题 |
交叉熵损失(Cross Entropy Loss)
在分类任务中,当目标分布 t \mathbf{t} t 和模型输出 z \mathbf{z} z 都是概率分布时,交叉熵是一种常用的损失函数,用于衡量两个分布之间的“差异”或“信息损失”。
定义:
给定两个概率分布 t = { t 1 , … , t C } \mathbf{t} = \{t_1, \dots, t_C\} t={t1,…,tC} 和 z = { z 1 , … , z C } \mathbf{z} = \{z_1, \dots, z_C\} z={z1,…,zC},交叉熵定义为:
CrossEntropy ( t , z ) = − ∑ i t i log z i \text{CrossEntropy}(t, z) = -\sum_i t_i \log z_i CrossEntropy(t,z)=−i∑tilogzi
推导展开:
交叉熵可以拆解为熵(Entropy)和 KL 散度(Kullback-Leibler Divergence)之和:
CrossEntropy ( t , z ) = − ∑ i t i log z i = − ∑ i t i log t i + ∑ i t i log t i z i = Entropy ( t ) + D KL ( t ∥ z ) \begin{aligned} \text{CrossEntropy}(t, z) &= -\sum_i t_i \log z_i \\ &= -\sum_i t_i \log t_i + \sum_i t_i \log \frac{t_i}{z_i} \\ &= \text{Entropy}(t) + D_{\text{KL}}(t \| z) \end{aligned} CrossEntropy(t,z)=−i∑tilogzi=−i∑tilogti+i∑tilogziti=Entropy(t)+DKL(t∥z)
其中:
- Entropy ( t ) = − ∑ i t i log t i \text{Entropy}(t) = -\sum_i t_i \log t_i Entropy(t)=−∑itilogti
- D KL ( t ∥ z ) = ∑ i t i log t i z i D_{\text{KL}}(t \| z) = \sum_i t_i \log \frac{t_i}{z_i} DKL(t∥z)=∑itilogziti
解释说明:
-
Entropy(熵) 是衡量分布不确定性的度量,值越高表示分布越“混乱”。
-
KL 散度 衡量两个分布之间的差异,是一个非对称的距离度量(即 D KL ( t ∥ z ) ≠ D KL ( z ∥ t ) D_{\text{KL}}(t \| z) \ne D_{\text{KL}}(z \| t) DKL(t∥z)=DKL(z∥t))。
面积越大 → 两分布差异越大 → KL 越大
图示直观理解:


总结:
| 名称 | 数学形式 | 说明 |
|---|---|---|
| 交叉熵 | − ∑ i t i log z i -\sum_i t_i \log z_i −∑itilogzi | 衡量预测分布 z z z 与真实分布 t t t 的差异 |
| 熵 | − ∑ i t i log t i -\sum_i t_i \log t_i −∑itilogti | 测量目标分布自身的不确定性 |
| KL 散度 | ∑ i t i log t i z i \sum_i t_i \log \frac{t_i}{z_i} ∑itilogziti | 模型 z z z 逼近目标 t t t 时的信息损失 |
因此,交叉熵 = 熵 + KL 散度,是一个包含两部分含义的损失函数。
2. Softmax
在多类分类中,输出层之前的softmax函数是为每个类分配条件概率
softmax ( z i ) = e z i ∑ j = 1 C e z j \text{softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^C e^{z_j}} softmax(zi)=∑j=1Cezjezi
3. 隐藏层权重更新与链式法则
我们首先来看从隐藏层到输出层的权重 w k j w_{kj} wkj(第 j j j 个隐藏神经元到第 k k k 个输出神经元)。
使用链式法则:
∂ J ∂ w k j = ∂ J ∂ net k ⋅ ∂ net k ∂ w k j = ∂ J ∂ net k ⋅ y j \frac{\partial J}{\partial w_{kj}} = \frac{\partial J}{\partial \text{net}_k} \cdot \frac{\partial \text{net}_k}{\partial w_{kj}} = \frac{\partial J}{\partial \text{net}_k} \cdot y_j ∂wkj∂J=∂netk∂J⋅∂wkj∂netk=∂netk∂J⋅yj
其中:
-
net k \text{net}_k netk 是输出神经元 k k k 的加权输入:
net k = ∑ j = 1 n H y j w k j + w k 0 \text{net}_k = \sum_{j=1}^{n_H} y_j w_{kj} + w_{k0} netk=j=1∑nHyjwkj+wk0 -
y j y_j yj 是隐藏层神经元 j j j 的激活输出
-
J J J 是整体损失函数,使用欧几里得损失:
J ( w ) = 1 2 ∥ t − z ∥ 2 J(\mathbf{w}) = \frac{1}{2} \|\mathbf{t} - \mathbf{z}\|^2 J(w)=21∥t−z∥2
即误差对每条连接的权重 w k j w_{kj} wkj 的导数,取决于该输出神经元的误差信号 ∂ J ∂ net k \frac{\partial J}{\partial \text{net}_k} ∂netk∂J 乘以隐藏层输入 y j y_j yj。
现在我们推导从输入层到隐藏层的权重 w j i w_{ji} wji(输入 x i x_i xi 到隐藏神经元 y j y_j yj)。
应用多级链式法则:
∂ J ∂ w j i = ∂ J ∂ y j ⋅ ∂ y j ∂ net j ⋅ ∂ net j ∂ w j i \frac{\partial J}{\partial w_{ji}} = \frac{\partial J}{\partial y_j} \cdot \frac{\partial y_j}{\partial \text{net}_j} \cdot \frac{\partial \text{net}_j}{\partial w_{ji}} ∂wji∂J=∂yj∂J⋅∂netj∂yj⋅∂wji∂netj
-
先求 ∂ net j ∂ w j i = x i \frac{\partial \text{net}_j}{\partial w_{ji}} = x_i ∂wji∂netj=xi
-
激活函数导数: ∂ y j ∂ net j = f ′ ( net j ) \frac{\partial y_j}{\partial \text{net}_j} = f'(\text{net}_j) ∂netj∂yj=f′(netj)
-
关键: ∂ J ∂ y j \frac{\partial J}{\partial y_j} ∂yj∂J 不能直接求出,但可以通过反向传播累加自输出层所有神经元:
∂ J ∂ y j = ∑ k = 1 C ∂ J ∂ z k ⋅ ∂ z k ∂ y j \frac{\partial J}{\partial y_j} = \sum_{k=1}^C \frac{\partial J}{\partial z_k} \cdot \frac{\partial z_k}{\partial y_j} ∂yj∂J=k=1∑C∂zk∂J⋅∂yj∂zk
- 其中 ∂ z k ∂ y j = f ′ ( net k ) ⋅ w k j \frac{\partial z_k}{\partial y_j} = f'(\text{net}_k) \cdot w_{kj} ∂yj∂zk=f′(netk)⋅wkj
- 若 z k z_k zk 是 softmax 输出, ∂ J ∂ net k = z k − t k \frac{\partial J}{\partial \text{net}_k} = z_k - t_k ∂netk∂J=zk−tk
所以完整形式为:
∂ J ∂ w j i = ( ∑ k ( z k − t k ) w k j ) ⋅ f ′ ( net j ) ⋅ x i \frac{\partial J}{\partial w_{ji}} = \left( \sum_k (z_k - t_k) w_{kj} \right) \cdot f'(\text{net}_j) \cdot x_i ∂wji∂J=(k∑(zk−tk)wkj)⋅f′(netj)⋅xi
总结
| 权重类型 | 梯度表达式 |
|---|---|
| 输出层 w k j w_{kj} wkj | ∂ J ∂ w k j = δ k ⋅ y j \frac{\partial J}{\partial w_{kj}} = \delta_k \cdot y_j ∂wkj∂J=δk⋅yj,其中 δ k = ∂ J ∂ net k \delta_k = \frac{\partial J}{\partial \text{net}_k} δk=∂netk∂J |
| 输入层 w j i w_{ji} wji | ∂ J ∂ w j i = δ j ⋅ x i \frac{\partial J}{\partial w_{ji}} = \delta_j \cdot x_i ∂wji∂J=δj⋅xi,其中 δ j \delta_j δj 由输出层误差反向传递计算得出 |
整个反向传播过程建立在链式法则之上,通过分层计算误差信号,并逐层传播与更新权重。
4. 梯度消失与爆炸问题
在深层神经网络中,误差信号需从输出层通过多层链式导数逐步反向传播至输入层。在此过程中,梯度可能出现以下数值不稳定现象:
梯度消失(vanishing gradients)
若激活函数的导数在大部分区域非常小(如 sigmoid 的最大导数仅为 0.25),那么反向传播时:
δ ( l ) = f ′ ( net ( l ) ) ⋅ ∑ k w k j ( l + 1 ) δ k ( l + 1 ) \delta^{(l)} = f'(\text{net}^{(l)}) \cdot \sum_k w_{kj}^{(l+1)} \delta_k^{(l+1)} δ(l)=f′(net(l))⋅k∑wkj(l+1)δk(l+1)
将不断被乘以小于 1 的数,导致越靠近输入层,梯度越趋近于 0,使得参数更新缓慢,甚至停滞。
梯度爆炸(exploding gradients)
相反,如果激活函数导数较大,或权重初始化不当(如值较大),则会导致链式乘积中项持续放大,最终使梯度数值迅速增大,导致训练不稳定甚至发散。
5. 应对策略与激活函数的选择
为了缓解梯度消失与爆炸问题,实践中可采用以下策略:
- 选用非饱和激活函数(如 ReLU、Leaky ReLU)以避免小梯度区间
- 使用归一化技巧(如 BatchNorm)以稳定各层输入分布
- 采用合适的权重初始化方式(如 Xavier 或 He 初始化)
- 在网络设计中控制层数与梯度路径长度
此外,近年来 Residual Connection(残差连接)和 Layer Normalization 等技术也在深层网络中得到广泛应用,用于缓解梯度问题。
综上所述,反向传播通过链式法则传播误差信号,是神经网络训练的核心机制。而要实现高效稳定的反向传播,需综合考虑激活函数选型、损失函数结构、权重初始化、归一化技术与模型深度等因素。
6. 随机梯度下降(SGD)与 Mini-batch 梯度下降
神经网络的训练本质上是通过优化某个损失函数 J ( θ ) J(\theta) J(θ) 来寻找最佳参数 θ \theta θ,最常用的方法是基于梯度的优化方式。
梯度下降(Gradient Descent)
标准的批量梯度下降(Batch Gradient Descent)在每一次更新中使用整个训练集:
θ ← θ − η ⋅ ∇ θ J ( θ ) \theta \leftarrow \theta - \eta \cdot \nabla_\theta J(\theta) θ←θ−η⋅∇θJ(θ)
- 优点:梯度方向准确
- 缺点:每次迭代计算成本高,不适合大数据集
随机梯度下降(SGD)
随机梯度下降在每次迭代中仅使用一个样本来估计梯度:
θ ← θ − η ⋅ ∇ θ J ( θ ; x ( i ) , y ( i ) ) \theta \leftarrow \theta - \eta \cdot \nabla_\theta J(\theta; x^{(i)}, y^{(i)}) θ←θ−η⋅∇θJ(θ;x(i),y(i))
- 优点:更新频繁、可以快速跳出局部极小值
- 缺点:单样本噪声大,收敛不稳定
权值更新可能会减少所呈现的单个模式上的误差,但会增加整个训练集上的误差。
小批量梯度下降(Mini-batch SGD)
Mini-batch 是在全批量和完全随机之间的折中策略。每次迭代使用一个包含 m m m 个样本的批次(mini-batch)计算梯度:
θ ← θ − η ⋅ 1 m ∑ i = 1 m ∇ θ J ( θ ; x ( i ) , y ( i ) ) \theta \leftarrow \theta - \eta \cdot \frac{1}{m} \sum_{i=1}^{m} \nabla_\theta J(\theta; x^{(i)}, y^{(i)}) θ←θ−η⋅m1i=1∑m∇θJ(θ;x(i),y(i))
- 一般选用 m = 32 , 64 , 128 m = 32, 64, 128 m=32,64,128 等较小值
- 兼具效率与稳定性,适用于现代硬件并行处理
训练流程
- 将训练集打乱并分成若干 mini-batches
- 对每个 mini-batch:
- 前向传播计算输出
- 反向传播计算梯度
- 更新权重参数
- 多轮迭代直到收敛
小结
| 方法 | 每次更新使用样本数 | 优点 | 缺点 |
|---|---|---|---|
| Batch | 全部训练样本 | 梯度稳定 | 内存消耗大、速度慢 |
| SGD | 单一样本 | 快速跳出局部最优 | 更新方向不稳定 |
| Mini-batch | 少量样本(如 64) | 训练速度与稳定性兼顾 | 最广泛使用的策略 |
使用 Mini-batch SGD 是现代深度学习训练的默认做法,通常配合动量、Adam 等优化器提升效果。
SGD 方法分析(SGD Analysis)
我们对两种常见的 SGD 训练方式进行优缺点对比分析:
单样本 SGD(One-example based SGD)
- 每次仅用一个样本估计梯度,因此噪声较大,更新方向波动明显
- 每次迭代开销小,比批量学习更快,尤其在数据存在冗余时效果更优
- 由于随机性高,噪声反而有助于跳出局部最小值
- 缺点是收敛路径不稳定,权重更新可能震荡,不一定收敛到稳定最优点
小批量 SGD(Mini-batch based SGD)
- 收敛性理论良好:梯度估计更平稳,易于分析收敛速度和稳定性
- 可结合批量加速技术(如 momentum、Adam、Nesterov)进行训练优化
- 由于噪声较小,更适合用于理论分析与调试模型行为
小结比较
| 项目 | 单样本 SGD | 小批量 SGD |
|---|---|---|
| 计算速度 | 每步快 | 中等 |
| 噪声/波动 | 大,有助于跳出局部最小值 | 小,梯度估计更稳定 |
| 收敛路径 | 易震荡,不一定收敛 | 更平稳,理论收敛性强 |
| 可结合技术 | 较少 | 支持大部分优化算法(如 Adam) |
| 理论分析难度 | 高 | 易于分析与调试 |
SGD 的噪声既是缺点也是优点,关键在于如何结合合适的 batch size 和优化器,以实现训练稳定性与收敛效率的平衡。
相关文章:

【深度学习】2. 从梯度推导到优化策略:反向传播与 SGD, Mini SGD
反向传播算法详解 1. 前向传播与输出层误差定义 假设我们考虑一个典型的前馈神经网络,其最后一层为 softmax 分类器,损失函数为交叉熵。 前向传播过程 对于某一隐藏层神经元 j j j: 输入: x i x_i xi 权重: w j…...
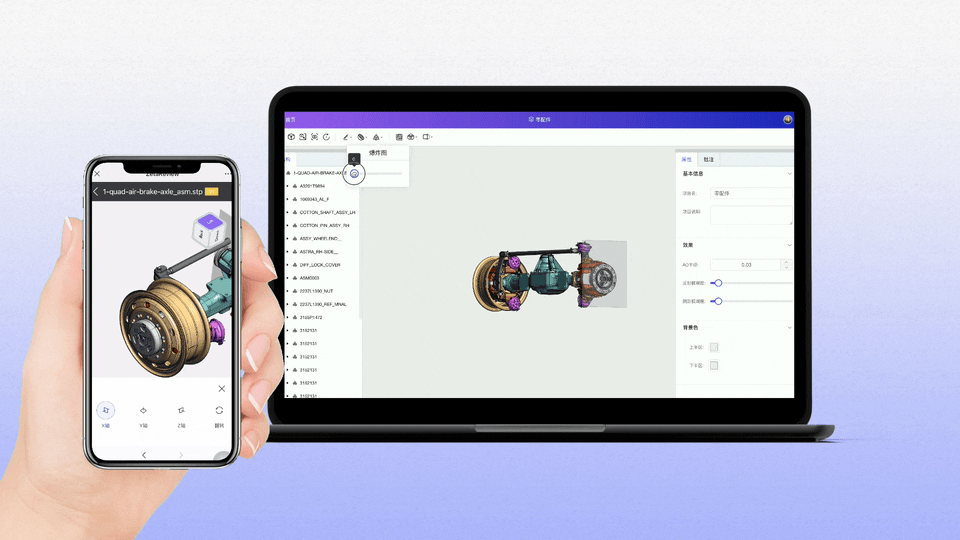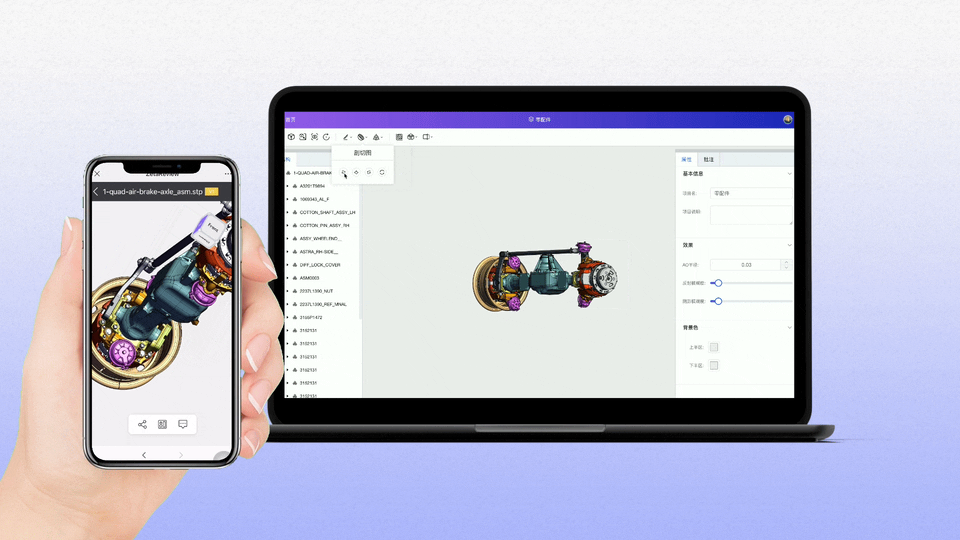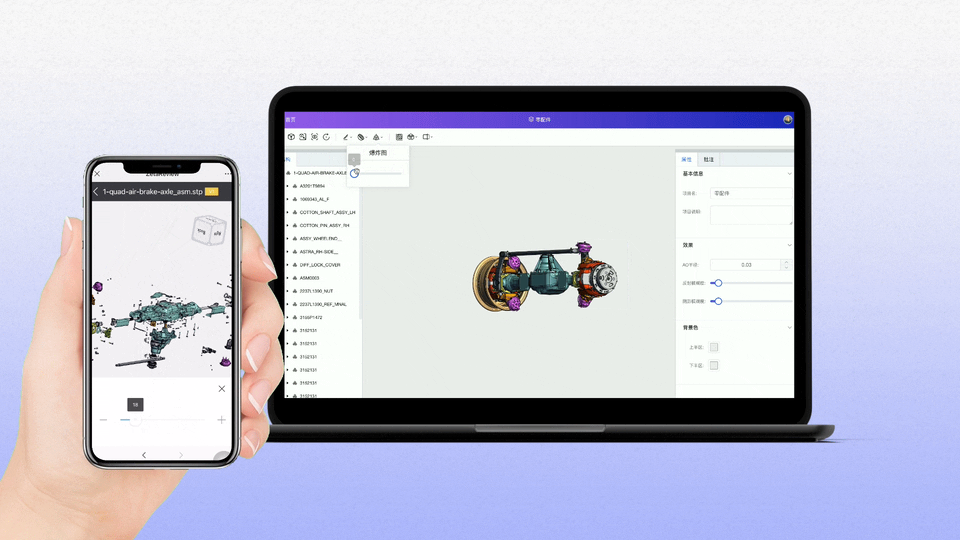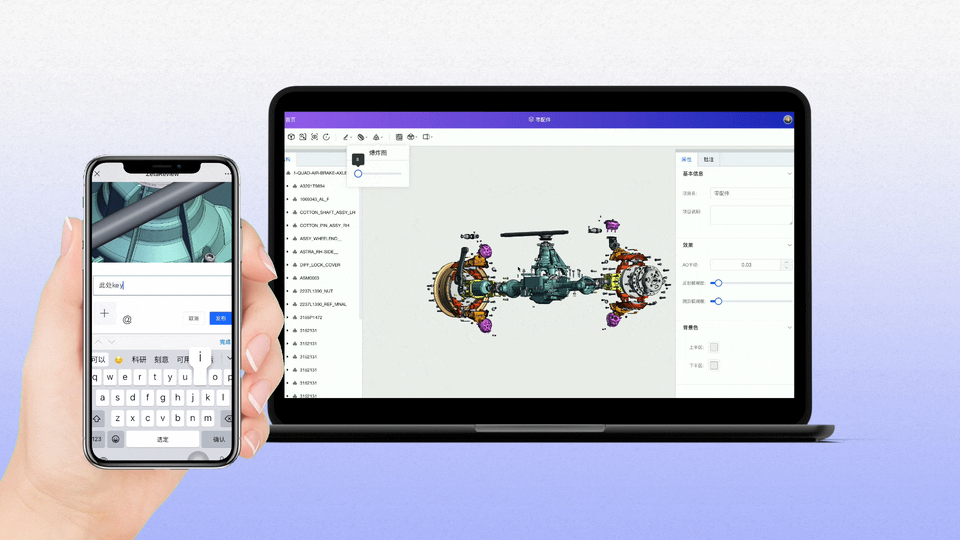
工业软件国产化:构建自主创新生态,赋能制造强国建设
随着全球产业环境的变化和技术的发展,建立自主可控的工业体系成为我国工业转型升级、走新型工业化道路、推动国家制造业竞争水平提升的重要抓手。 市场倒逼与政策护航,国产化进程双轮驱动 据中商产业研究院预测,2025年中国工业软件市场规模…...

UART、RS232、RS485基础知识
一、UART串口通信介绍 UART是一种采用异步串行、全双工通信方式的通用异步收发传输器功能。 硬件电路: •简单双向串口通信有两根通信线(发送端TX和接收端RX) •TX与RX要交叉连接 •当只需单向的数据传输时,可以只接一根通信线…...

AI重塑数据治理的底层逻辑
AI重塑数据治理的底层逻辑 人治模式:一个必然失败的商业逻辑智治模式:重新定义数据治理的商业模式结语 上个月,一位老友约我喝茶。他是某知名互联网公司的数据总监,聊天时满脸愁容。 “润总,我们公司数据治理团队有50多…...

基于 AI 实现阿里云的智能财务管家
新钛云服已累计为您分享844篇技术干货 为了解决传统账单处理中人工查询效率低下、响应速度慢及易出错等问题,同时顺应AI技术发展趋势,提升服务智能化水平。随着业务规模扩大和账单数据复杂度增加,人工处理已难以满足高效管理需求。我们想到通…...

【成品论文】2025年电工杯数学建模竞赛B题50页保奖成品论文+matlab/python代码+数据集等(后续会更新)
文末获取资料 多约束条件下城市垃圾分类运输调度问题 摘要 随着城市化进程加快,城市生活垃圾产量持续增长,垃圾分类运输已成为城市环境治理的关键环节。本文针对城市垃圾分类运输中的路径优化与调度问题,综合考虑不同垃圾类型、车辆载重约束…...

IIS文件上传漏洞绕过:深入解析与高效防御
目录 一、IIS解析漏洞的底层逻辑 二、绕过技巧:从基础到高级 1. 分号截断与路径拼接(经典手法) 2. 目录解析漏洞利用 3. 操作系统特性与字符混淆 4. 扩展名黑名单绕过 5. 结合其他…...

【node.js】数据库与存储
个人主页:Guiat 归属专栏:node.js 文章目录 1. 数据库概述1.1 数据库在Node.js中的作用1.2 Node.js支持的数据库类型 2. 关系型数据库集成2.1 MySQL与Node.js2.1.1 安装MySQL驱动2.1.2 建立连接2.1.3 执行CRUD操作 2.2 PostgreSQL与Node.js2.2.1 安装pg驱…...

leetcode2081. k 镜像数字的和-hard
1 题目:k 镜像数字的和 官方标定难度:难 一个 k 镜像数字 指的是一个在十进制和 k 进制下从前往后读和从后往前读都一样的 没有前导 0 的 正 整数。 比方说,9 是一个 2 镜像数字。9 在十进制下为 9 ,二进制下为 1001 ÿ…...

Halcon 单目相机标定测量
文章目录 双面相机标定链接一维测量gen_cam_par_area_scan_division -为区域扫描相机生成一个相机参数元组,该相机的变形由分割模型建模。(相机自带参数)create_calib_data -创建Halcon 数据标定模型set_calib_data_cam_param -设置校准数据模型中摄像机的类型和初始…...

git子模块--常见操作
克隆仓库 标准化克隆流程 基本命令git clone <父仓库远程URL> [本地文件名] cd <本地仓库名> git submodule init # 初始化子模块配置 git submodule update # 拉取子模块内容一次性完成克隆和初始化流程 基本命令git clone --recurse-submodules <父仓库远…...
——创建和更新统计对象)
解决SQL Server SQL语句性能问题(9)——创建和更新统计对象
9.3. 创建和更新统计对象 与Oracle中的统计数据相对应,SQL Server中的统计对象,本专栏6.3节中也提到,数据库CBO依赖其为SQL语句产生最合适、最高效的查询计划。数据库CBO结合各类统计对象,并利用其内置的、复杂而高级的模型与算法,尽可能的为SQL语句计算和评估出所有候选…...

数据被泄露了怎么办?
数据泄露是严重的网络安全事件,需立即采取行动以降低风险。以下是关键应对步骤: 1. 确认泄露范围 核实泄露内容:确定泄露的是密码、财务信息、身份证号还是其他敏感数据。 评估来源:检查是个人设备被入侵、某平台漏洞,…...

绩效管理缺乏数据支持,如何提高客观性?
要提高绩效管理的客观性,应从建立科学的指标体系、加强数据采集手段、引入自动化绩效工具、强化过程记录机制、定期评估与反馈优化五大方面着手。其中,建立科学的指标体系是关键基础。没有数据支撑的绩效体系,往往容易陷入主观打分、个人偏见…...

unity控制相机围绕物体旋转移动
记录一下控制相机围绕物体旋转与移动的脚本,相机操作思路分为两块,一部分为旋转,一部分为移动,旋转是根据当前center中心点的坐标,根据距离设置与默认的旋转进行位置移动,移动是根据相机的左右和前后进行计…...

线性代数:AI大模型的数学基石
🧑 博主简介:CSDN博客专家、CSDN平台优质创作者,高级开发工程师,数学专业,10年以上C/C, C#, Java等多种编程语言开发经验,拥有高级工程师证书;擅长C/C、C#等开发语言,熟悉Java常用开…...

【C/C++】从零开始掌握Kafka
文章目录 从零开始掌握Kafka一、Kafka 基础知识理解(理论)1. 核心组件与架构2. 重点概念解析 二、Kafka 面试重点知识梳理三、C 使用 Kafka 的实践(librdkafka)1. librdkafka 简介2. 安装 librdkafka 四、实战:高吞吐生…...

02_redis分布式锁原理
文章目录 一、redis如何实现分布式锁1. 使用 SETNX 命令2. 设置过期时间3. 释放锁4. 注意事项5. 示例代码 二、Java中分布式锁如何设置超时时间1. Redis分布式锁2. 基于Zookeeper的分布式锁3. 基于数据库的分布式锁注意事项 一、redis如何实现分布式锁 Redis 实现分布式锁是一…...

简单血条于小怪攻击模板
创建一个2d正方形(9-Sliced)命名为Player,在Player下面新建一个画布(Canvas)命名为PlayerHealthUI,在画布下面新建一个滑动条(Slider)命名为HealthBar 把PlayerHealthUI脚本挂载到Pl…...

Win11 系统登入时绑定微软邮箱导致用户名欠缺
Win11 系统登入时绑定微软邮箱导致用户名欠缺 解决思路 -> 解绑当前微软邮箱和用户名 -> 断网离线建立本地账户 -> 设置本地账户为Admin权限 -> 注销当前账户,登入新建的用户 -> 联网绑定微软邮箱 -> 删除旧的用户命令步骤 管理员权限打开…...

代码随想录算法训练营第四十六四十七天
卡码网题目: 110. 字符串接龙105. 有向图的完全联通106. 岛屿的周长107. 寻找存在的路径 其他: 今日总结 往期打卡 110. 字符串接龙 跳转: 110. 字符串接龙 学习: 代码随想录公开讲解 问题: 字典 strList 中从字符串 beginStr 和 endStr 的转换序列是一个按下述规格形成的序…...

华硕FL8000U加装16G+32G=48G内存条
华硕FL8000U加装16G32G48G内存条 一、华硕FL8000U加装内存条endl 一、华硕FL8000U加装内存条 相关视频链接: https://www.bilibili.com/video/BV1gw4dePED8/ endl...

前后端联调实战指南:Axios拦截器、CORS与JWT身份验证全解析
前言 在现代Web开发中,前后端分离架构已成为主流,而前后端联调则是开发过程中不可避免的关键环节。本文将深入探讨前后端联调中的三大核心技术:Axios拦截器的灵活运用、CORS跨域问题的全面解决方案以及JWT身份验证的安全实现。通过本文&…...

java高级 -Junit单元测试
Junit单元测试就是针对最小的功能:方法,编写测试代码对其进行正确性测试。用main方法进行测试的弊端是一个方法测试失败可能会影响别的方法的测试,也无法得到测试报告,需要我们自己观察数据是否正确。 此时,我们就需要…...

在 UVM验证环境中,验证 Out-of-Order或 Interleaving机制
在 UVM验证环境中,验证 Out-of-Order或 Interleaving机制 摘要:在 UVM (Universal Verification Methodology) 验证环境中,验证 Out-of-Order (乱序) 或 Interleaving (交错) 机制是验证复杂 SoC (System on Chip) 设计的重要任务,尤其是在验证高速接口(如 PCIe、AXI)、缓…...

V9数据库替换授权
文章目录 环境文档用途详细信息 环境 系统平台:Linux x86-64 Red Hat Enterprise Linux 7 版本:9.0 文档用途 1、本文档用于指导V9数据库替换授权。 2、V9数据库授权文件为license.dat。 详细信息 1、上传新的授权文件到服务器并修改授权文件属主为…...

勇闯Chromium—— Chromium的多进程架构
问题 构建一个永不崩溃或挂起的渲染引擎几乎是不可能的,构建一个绝对安全的渲染引擎也几乎是不可能的。 从某种程度上来说,2006 年左右的网络浏览器状态与过去单用户、协作式多任务操作系统的状况类似。正如在这样的操作系统中,一个行为不端的应用程序可能导致整个系统崩溃…...

Go语言中常量的命名规则详解
1. 常量的基本命名规则 1.1. 命名格式 1. 使用const关键字声明; 2. 命名格式:const 常量名 [类型] 值; 3. 类型可以省略,由编译器推断; 1.2. 命名风格 大小写规则: 1. 首字母大写:导出常…...

软件质量保证与测试实验
课程 软件质量保证与测试 目的:练习软件测试中白盒测试方法 内容: 测试如下程序段: #include <stdio.h>int main() {int i 1, n1 0, n2 0;float sum 0.0;float average;float score[100];printf("请输入分…...

历年华东师范大学保研上机真题
2025华东师范大学保研上机真题 2024华东师范大学保研上机真题 2023华东师范大学保研上机真题 在线测评链接:https://pgcode.cn/school?classification1 简单一位数代数式计算 题目描述 给一个小学生都会算的1位数与1位数运算的代数式,请你求出这个表…...
