leetcode513.找树左下角的值:递归深度优先搜索中的最左节点追踪之道
一、题目本质与核心诉求解析
在二叉树算法问题中,"找树左下角的值"是一个典型的结合深度与位置判断的问题。题目要求我们找到二叉树中最深层最左边的节点值,这里的"左下角"有两个关键限定:
- 深度优先:必须是深度最大的那一层节点
- 最左优先:在最深层中选择最左边的那个节点
先来看一个示例二叉树:
1/ \2 3/ / \
4 5 6/7
在这个树中,最深层是第3层(根节点为第0层时是第2层),该层最左节点是7,因此正确输出为7。理解这个问题的核心在于如何在递归过程中同时追踪节点深度和左右位置关系,这也是本文要重点解析的内容。
二、递归解法的核心实现与数据结构设计
完整递归代码实现
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {private int Deep = -1; // 记录当前最大深度private int res = 0; // 记录最深层最左节点值public int findBottomLeftValue(TreeNode root) {findLeftVal(root, 0); // 从根节点开始,深度初始为0return res;}public void findLeftVal(TreeNode root, int deep) {if (root == null) {return;}// 处理叶子节点:判断是否更新最深层最左节点if (root.left == null && root.right == null) {if (deep > Deep) {res = root.val;Deep = deep;}return;}// 先递归左子树,保证左子树优先访问if (root.left != null) {findLeftVal(root.left, deep + 1);}// 再递归右子树if (root.right != null) {findLeftVal(root.right, deep + 1);}}
}
关键数据结构设计解析
-
Deep变量:
- 作用:记录当前发现的最大深度
- 初始值:-1(因为根节点深度从0开始,确保第一个叶子节点会更新该值)
- 更新时机:当遇到更深的叶子节点时更新
-
res变量:
- 作用:存储最深层最左节点的值
- 更新原则:仅当遇到更深的叶子节点,或者同深度但更左的叶子节点时更新(由于先左后右递归,同深度下左节点必然先访问)
-
deep参数:
- 作用:当前递归层的节点深度
- 传递方式:每次递归进入子节点时深度+1
- 意义:明确当前节点在树中的层级位置
三、核心问题解析:递归中如何判断最深层最左节点
1. 深度优先搜索的顺序控制
本算法采用先左后右的深度优先搜索顺序,这是确保找到"最左"节点的关键:
- 递归调用顺序:先处理左子树,再处理右子树
- 核心逻辑:在同一深度下,左子树的节点会比右子树的节点先被访问
- 效果:当存在多个同深度节点时,左节点会优先被判定为当前最深层最左节点
2. 深度判断与更新机制
if (root.left == null && root.right == null) {if (deep > Deep) {res = root.val;Deep = deep;}
}
- 叶子节点判断:当节点左右子树都为空时,确定为叶子节点
- 深度比较:如果当前叶子节点深度大于已记录的最大深度
Deep,则更新结果 - 更新策略:
- 更深的叶子节点:直接更新res和Deep
- 同深度的叶子节点:由于先左后右递归,左节点先访问,res不会被右节点覆盖
3. 递归终止与回溯逻辑
- 终止条件:
- 遇到空节点时直接返回(递归边界)
- 处理完叶子节点后返回(不再继续递归)
- 回溯作用:当左子树递归完成后,回溯到父节点,再进入右子树递归,确保左右子树都被遍历
四、递归流程深度模拟:以示例二叉树为例
示例二叉树结构(根节点深度为0):
1(0)/ \2(1) 3(1)/ / \
4(2) 5(2) 6(2)/7(3)
详细递归执行过程
-
初始状态:
Deep = -1,res = 0- 调用
findLeftVal(root, 0),root为节点1,深度0
-
处理节点1(深度0):
- 非叶子节点,进入左子树调用
findLeftVal(2, 1)
- 非叶子节点,进入左子树调用
-
处理节点2(深度1):
- 非叶子节点,进入左子树调用
findLeftVal(4, 2)
- 非叶子节点,进入左子树调用
-
处理节点4(深度2):
- 是叶子节点(左右子树为空)
- 深度2 > Deep(-1),更新
res=4,Deep=2 - 返回上一层(节点2)
-
节点2的右子树为空,返回上一层(节点1)
-
节点1进入右子树调用
findLeftVal(3, 1) -
处理节点3(深度1):
- 非叶子节点,进入左子树调用
findLeftVal(5, 2)
- 非叶子节点,进入左子树调用
-
处理节点5(深度2):
- 非叶子节点,进入左子树调用
findLeftVal(7, 3)
- 非叶子节点,进入左子树调用
-
处理节点7(深度3):
- 是叶子节点
- 深度3 > Deep(2),更新
res=7,Deep=3 - 返回上一层(节点5)
-
节点5的右子树为空,返回上一层(节点3)
-
节点3进入右子树调用
findLeftVal(6, 2) -
处理节点6(深度2):
- 是叶子节点
- 深度2 < Deep(3),不更新res
- 返回上一层(节点3)
-
所有递归结束,返回res=7
五、算法复杂度与递归特性分析
1. 时间复杂度分析
- O(n):每个节点仅被访问一次,n为树的节点总数
- 原因:递归过程中对每个节点进行一次深度判断,无重复访问
2. 空间复杂度分析
- O(h):h为树的高度,取决于递归栈的最大深度
- 最坏情况:树退化为链表时,h=n,空间复杂度O(n)
- 平均情况:平衡二叉树h=logn,空间复杂度O(logn)
3. 递归算法的优势与局限
| 优势 | 局限 |
|---|---|
| 代码逻辑简洁,符合树的递归定义 | 可能因栈溢出无法处理极大树 |
| 天然支持深度优先搜索顺序控制 | 空间复杂度与树深度相关 |
| 先左后右的递归顺序自然实现"最左"优先 | 调试相比迭代更困难 |
六、核心技术点总结:递归找最左节点的三大关键
1. 深度优先搜索顺序控制
- 先左后右的递归顺序是实现"最左"优先的核心
- 递归天然保证左子树先于右子树处理,确保同深度下左节点优先被访问
2. 深度追踪与比较机制
- 通过参数传递当前深度,全局变量记录最大深度
- 叶子节点处进行深度比较,确保只保留最深层节点
3. 优先更新策略
- 深度更大时:无条件更新结果
- 深度相同时:由于左子树先处理,结果不会被右节点覆盖
- 实现了"深度优先,同深度左优先"的判定逻辑
七、拓展思考:递归与迭代解法的对比与适用场景
1. 与层序遍历迭代法的对比
| 方法 | 核心思想 | 时间复杂度 | 空间复杂度 | 优势场景 |
|---|---|---|---|---|
| 递归 | 深度优先+先左后右 | O(n) | O(h) | 代码简洁、树深度较小 |
| 迭代 | 广度优先+层序处理 | O(n) | O(m)(m为最大层宽度) | 处理极大树、避免栈溢出 |
2. 大厂面试中的策略建议
- 当树深度较小时,递归解法更简洁高效
- 当树可能很深时,应考虑迭代解法避免栈溢出
- 面试中可先给出递归解法,再主动说明迭代优化方向
八、总结:递归解法的核心设计哲学
本递归算法通过"深度优先搜索+先左后右顺序+深度追踪"的组合策略,巧妙解决了找树左下角值的问题。其核心设计哲学包括:
- 深度优先的天然优势:递归天然适合深度优先搜索,能自然追踪节点深度
- 顺序控制的重要性:先左后右的递归顺序是实现"最左"优先的关键
- 状态传递的巧妙设计:通过参数传递深度,全局变量记录结果,实现状态追踪
- 叶子节点的关键作用:仅在叶子节点处判断是否更新结果,提高算法效率
理解这种递归设计思路,不仅能解决本题,还能为类似的二叉树深度与位置相关问题提供通用解法。在实际应用中,可根据树的规模和场景选择递归或迭代实现,灵活应对不同需求。
相关文章:

leetcode513.找树左下角的值:递归深度优先搜索中的最左节点追踪之道
一、题目本质与核心诉求解析 在二叉树算法问题中,"找树左下角的值"是一个典型的结合深度与位置判断的问题。题目要求我们找到二叉树中最深层最左边的节点值,这里的"左下角"有两个关键限定: 深度优先:必须是…...

基于Flink的数据中台管理平台
基于Flink做的数据中台工程项目。数据从source到clickhouse全流程的验证。集成元数据管、数据资产、数据发现功能,自主管理元数据变更,集成元数据版本管理。 同时,对整个大数据集群使用到的组件或者是工具进行管理。比如nacos、kafka、zookee…...

AI-Ready TapData:如何基于 MCP 协构建企业级 AI 实时数据中枢?(含教程)
随着企业对私有大模型、行业大模型的探索逐渐深入,“AI应用是否真正落地”,越来越取决于企业是否拥有结构化、实时、可交互的高质量数据。而现实是,大多数企业的核心业务数据依旧被困在多个异构系统、孤岛数据库和 ETL 流程之中,导…...

Spring Boot 登录实现:JWT 与 Session 全面对比与实战讲解
Spring Boot 登录实现:JWT 与 Session 全面对比与实战讲解 2025.5.21-23:11今天在学习黑马点评时突然发现用的是与苍穹外卖jwt不一样的登录方式-Session,于是就想记录一下这两种方式有什么不同 在实际开发中,登录认证是后端最基础也是最重要…...

【HTML-5】HTML 实体:完整指南与最佳实践
1. 什么是 HTML 实体? HTML 实体是一种在 HTML 文档中表示特殊字符的方法,这些字符如果直接使用可能会与 HTML 标记混淆,或者无法通过键盘直接输入。实体由 & 符号开始,以 ; 分号结束。 <p>这是一个小于符号的实体&am…...

SpringBoot 项目实现操作日志的记录(使用 AOP 注解模式)
本文是博主在做关于如何记录用户操作日志时做的记录,常见的项目中难免存在一些需要记录重要日志的部分,例如权限和角色设定,重要数据的操作等部分。 博主使用 Spring 中的 AOP 功能,结合注解的方式,对用户操作过的一些…...

AI|Java开发 IntelliJ IDEA中接入本地部署的deepseek方法
目录 连接本地部署的deepseek: IntelliJ IDEA中使用deepseek等AI: 用法一:让AI写代码 用法二:选中这段代码,右键,可以让其解释这段代码的含义。这时显示的解释是英文的。 连接本地部署的deepseek&#…...

【疑难杂症】Vue前端下载文件无法打开 已解决
由于刚学了VUE不久,不清楚底层逻辑。我遇到从后台下载文件无法打开的问题。 测试下来是,请求时未设置 responseType: blob。 axios 默认的 responseType 是 json ,会尝试将响应体解析为JSON。但文件下载场景需要后端返回二进制流࿰…...

【1——Android端添加隐私协议(unity)1/3】
前言:这篇仅对于unity 发布Android端上架国内应用商店添加隐私协议,隐私协议是很重要的东西,没有这个东西,是不上了应用商店的。 对于仅仅添加隐私协议,我知道有三种方式,第一种和第二种基本一样 1.直接在unity里面新…...

Linux之概述和安装vm虚拟机
文章目录 操作系统概述硬件和软件操作系统常见操作系统 初识LinuxLinux的诞生Linux内核Linux发行版 虚拟机介绍虚拟机 VMware WorkStation安装虚拟化软件VMware WorkStation 安装查看VM网络连接设置VM存储位置 在VMware上安装Linux(发行版CentOS7)安装包获取CentOS7 安装 Mac系…...

深入理解 Linux 的 set、env 和 printenv 命令
在 Linux 和类 Unix 系统中,环境变量是配置和管理 Shell 及进程行为的核心机制。set、env 和 printenv 是与环境变量交互的三个重要命令,每个命令都有其独特的功能和用途。本文将详细探讨这三个命令的区别,帮助大家更好地理解和使用这些命令。…...
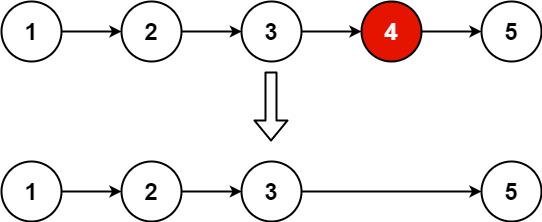
LeetCode热题100--19.删除链表的倒数第N个结点--中等
1. 题目 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。 示例 1: 输入:head [1,2,3,4,5], n 2 输出:[1,2,3,5] 示例 2: 输入:head [1], n 1 输出:[] 示例…...

开发AR导航助手:ARKit+Unity+Mapbox全流程实战教程
引言 在增强现实技术飞速发展的今天,AR导航应用正逐步改变人们的出行方式。本文将手把手教你使用UnityARKitMapbox开发跨平台AR导航助手,实现从虚拟路径叠加到空间感知的完整技术闭环。通过本教程,你将掌握: AR空间映射与场景理…...

git学习与使用(远程仓库、分支、工作流)
文章目录 前言简介git的工作流程git的安装配置git环境:git config --globalgit的基本使用新建目录初始化仓库(repository)添加到暂存区新增/修改/删除 文件状态会改变 提交到仓库查看提交(commit)的历史记录git其他命令…...

嵌入式预处理链接脚本lds和map文件
在嵌入式开发中,.lds.S 文件是一个 预处理后的链接脚本(Linker Script),它结合了 C 预处理器(Preprocessor) 的功能和链接脚本的语法。它的核心作用仍然是 定义内存布局和链接规则,但通过预处理…...

9. Spring AI 各版本的详细功能与发布时间整理
目录 一、旧版本(Legacy) 0.8.1(2024年3月) 二、里程碑版本(Milestone) 1.0.0-M1(2024年5月30日) 1.0.0-M2(2024年7月) 1.0.0-M3(2024年10月8日) 1.0.0-M4(2024年12月) 1.0.0-M5(2025年1月9日) 1.0.0-M6(2025年3月) 1.0.0-M7(2025年4月14日) 1.…...

《Android 应用开发基础教程》——第十四章:Android 多线程编程与异步任务机制(Handler、AsyncTask、线程池等)
目录 第十四章:Android 多线程编程与异步任务机制(Handler、AsyncTask、线程池等) 🔸 14.1 为什么需要多线程? 🔸 14.2 Handler Thread 模型 ✦ 使用 Handler 与 Thread 进行线程通信 ✦ 简要说明&am…...

Apache 高级配置实战:从连接保持到日志分析的完整指南
Apache 高级配置实战:从连接保持到日志分析的完整指南 前言 最近在深入学习 Apache 服务器配置时,发现很多朋友对 Apache 的高级功能还不够了解。作为一个在运维路上摸爬滚打的技术人,我想把这些实用的配置技巧分享给大家。今天这篇文章会带…...
身份提供方(IdP)、iam选型)
开源 OIDC(OpenID Connect)身份提供方(IdP)、iam选型
文章目录 开源 OIDC(OpenID Connect)身份提供方(IdP)、iam选型主流开源 OIDC(OpenID Connect)身份提供方(IdP)zitadeldexory开源 OIDC(OpenID Connect)身份提供方(IdP)、iam选型 主流开源 OIDC(OpenID Connect)身份提供方(IdP) 当前主流的**开源 OIDC(OpenI…...

Android OkHttp控制链:深入理解网络请求的流程管理
OkHttp作为Android和Java平台上广泛使用的HTTP客户端,其核心设计之一就是"控制链"(Chain)机制。本文将深入探讨OkHttp控制链的工作原理、实现细节以及如何利用这一机制进行高级定制。 一、什么是OkHttp控制链 OkHttp控制链是一种责任链模式的实现&#…...

【JVM 01-引言入门篇】
JVM 引言篇01 笔记记录 1. 什么是JVM?2. 学习JVM有什么用?3. 常见的JVM4. 学习路线 学习资料来源-b站黑马 1. 什么是JVM? 定义:Java虚拟机(Java Virtual Machine 简称JVM)是运行所有Java程序的抽象计算机&a…...

Pandas数据规整
(1)层次化索引 1.创建带层次化索引的df 第一种,直接创建 import pandas as pd import numpy as npdata pd.Series(np.random.randn(9),index [[a, a, a, b, b, c, c, d, d],[1, 2, 3, 1, 3, 1, 2, 2, 3]]) print(data) # a 1 -0.6416…...

ThreadLocal线程本地变量在dubbo服务使用时候遇到的一个坑
我昨天遇到一个问题,就是我springboot项目里面有一个提供代办服务审核的dubbo接口,这个接口给房源项目调用,但是碰到一个问题就是,房源项目每天凌晨5点会查询满足条件过期的数据,然后调用我这边的代办审核dubbo接口&am…...

pga 作用
Oracle pga的作用 PGA 内存结构与功能解释: PGA ├── 1. Private SQL Area ├── 2. Session Memory ├── 3. SQL Work Areas │ ├── Sort Area │ ├── Hash Area │ ├── Bitmap Merge Area │ └── Bitmap Create Area └── 4. Stack S…...

setup.py Pip wheel
. ├── my_package │ ├── __init__.py │ └── my_file.py └── setup.pymy_file.py def my_func():print("Hello World")setup.py from setuptools import setup, find_packages import datetimesetup(namemy_package, # 记得改version0.1.1,packag…...

GO 语言进阶之 时间处理和Json 处理
更多个人笔记见: github个人笔记仓库 gitee 个人笔记仓库 个人学习,学习过程中还会不断补充~ (后续会更新在github上) 文章目录 时间处理基本例子 Json处理基础案例 时间处理 时间格式化必须使用:2006-01-…...

对WireShark 中的UDP抓包数据进行解析
对WireShark 中的UDP抓包数据进行解析 本文尝试对 WireShark 中抓包的 UDP 数据进行解析。 但是在尝试对 TCP 中的 FTP 数据进行解析的时候,发现除了从端口号进行区分之外, 没有什么好的方式来进行处理。 import numpy as np import matplotlib.pyplot …...
)
Flannel后端为UDP模式下,分析数据包的发送方式(二)
发往 10.244.2.5 的数据包最终会经过物理网卡 enp0s3,尽管路由表直接指定通过 flannel.1 发出。以下以 Markdown 格式详细解释为什么会经过 enp0s3,结合 Kubernetes 和 Flannel UDP 模式的背景。 问题分析 在 Kubernetes 环境中,使用 Flanne…...

从 0 到 1:Spring Boot 与 Spring AI 深度实战(基于深度求索 DeepSeek)
在人工智能技术与企业级开发深度融合的今天,传统软件开发模式与 AI 工程化开发的差异日益显著。作为 Spring 生态体系中专注于 AI 工程化的核心框架,Spring AI通过标准化集成方案大幅降低 AI 应用开发门槛。本文将以国产大模型代表 ** 深度求索ÿ…...

upload-labs通关笔记-第20关 文件上传之杠点绕过
系列目录 upload-labs通关笔记-第1关 文件上传之前端绕过(3种渗透方法) upload-labs通关笔记-第2关 文件上传之MIME绕过-CSDN博客 upload-labs通关笔记-第3关 文件上传之黑名单绕过-CSDN博客 upload-labs通关笔记-第4关 文件上传之.htacess绕过-CSDN…...
