LeetCode --- 450周赛
题目列表
3550. 数位和等于下标的最小下标
3551. 数位和排序需要的最小交换次数
3552. 网格传送门旅游
3553. 包含给定路径的最小带权子树 II
一、数位和等于下标的最小下标

直接模拟计算数位和即可,代码如下
// C++
class Solution {
public:int smallestIndex(vector<int>& nums) {int n = nums.size();for(int i = 0; i < n; i++){int x = nums[i], s = 0;while(x){s += x % 10;x /= 10;}if(s == i)return i;}return -1;}
};
# Python
class Solution:def smallestIndex(self, nums: List[int]) -> int:n = len(nums)for i, x in enumerate(nums):s = 0while x:s += x % 10x //= 10if i == s:return ireturn -1
二、数位和排序需要的最小交换次数

由于我们可以通过排序得到每个数的最终位置,所以这题就转换成了给你两个元素相同的序列 A、B,要求将 A 通过交换转换成 B 的最小操作次数,通过对需要交换的位置加上有向边进行建图,问题就变成了对给定的有向图,如何使得它们各自成为一个独立的环的操作次数最少

这里有一个结论:最少的交换次数为结点的个数减去环的个数
代码如下(关键就是计算环的个数)
// C++
class Union{
public:Union(int n):fa(n),cnt(n){iota(fa.begin(), fa.end(), 0);}void merge(int x, int y){int fa_x = find(x), fa_y = find(y);if(fa_x != fa_y){cnt--;fa[fa_x] = fa_y;}}int find(int x){int pa = x;while(pa != fa[pa]){pa = fa[pa];}while(x != pa){int tmp = fa[x];fa[x] = pa;x = tmp;}return pa;}int count(){return cnt;}
private:vector<int> fa;int cnt;
};
class Solution {
public:int minSwaps(vector<int>& nums) {int n = nums.size();vector<array<int, 3>> a(n);for (int i = 0; i < n; i++) {int s = 0;for (int x = nums[i]; x > 0; x /= 10) {s += x % 10;}a[i] = {s, nums[i], i};}ranges::sort(a);Union un(n);for(int i = 0; i < n; i++){un.merge(i, a[i][2]);}return n - un.count();}
};// 迭代
class Solution {
public:int minSwaps(vector<int>& nums) {int n = nums.size();vector<array<int, 3>> a(n);for (int i = 0; i < n; i++) {int s = 0;for (int x = nums[i]; x > 0; x /= 10) {s += x % 10;}a[i] = {s, nums[i], i};}ranges::sort(a);int c = 0;for(int i = 0; i < n; i++){if(a[i][2] < 0) continue;c++;int j = i;while(a[j][2] >= 0){int nxt = a[j][2];a[j][2] = -1;j = nxt;}}return n - c;}
};
三、网格传送门旅游
很经典的最短路问题,可以用 Dijkstra算法 来解决,需要注意的每种传送门最多传送一次,重复传送显然是无意义的,A1->A2->A3 不如直接 A1->A3,代码如下
// C++
class Solution {static constexpr int dirs[4][2] = {{0,1}, {0,-1}, {1,0}, {-1,0}};
public:int minMoves(vector<string>& matrix) {int n = matrix.size(), m = matrix[0].size();vector<vector<pair<int,int>>> g(26);for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){if(isalpha(matrix[i][j])){g[matrix[i][j] - 'A'].emplace_back(i, j);}}}priority_queue<tuple<int,int,int>, vector<tuple<int,int,int>>, greater<>> pq;pq.emplace(0, 0, 0);vector dist(n, vector<int>(m, INT_MAX));dist[0][0] = 0;while(pq.size()){auto [d, x, y] = pq.top(); pq.pop();if(x == n - 1 && y == m - 1) return d;if(d != dist[x][y]) continue;if(isalpha(matrix[x][y])){int i = matrix[x][y] - 'A';for(auto [xi, yi] : g[i]){if(dist[xi][yi] > d){dist[xi][yi] = d;pq.emplace(d, xi, yi);}}g[i].resize(0);}for(int i = 0; i < 4; i++){int xi = x + dirs[i][0], yi = y + dirs[i][1];if(xi < 0 || xi >= n || yi < 0 || yi >= m || matrix[xi][yi] == '#' || dist[xi][yi] <= d + 1)continue;dist[xi][yi] = d + 1;pq.emplace(d + 1, xi, yi);}}return -1;}
};// 0-1 bfs
// 由于本题的距离只有 +0 / +1 两种选项,所以这里可以直接用双端队列模拟优先级队列(堆)
// +0 的距离依旧是队列中最小的距离,所以头插
// +1 的距离会成为最大值,所以尾插,如果不理解,建立手动模拟一下
class Solution {static constexpr int dirs[4][2] = {{0,1}, {0,-1}, {1,0}, {-1,0}};
public:int minMoves(vector<string>& matrix) {int n = matrix.size(), m = matrix[0].size();vector<vector<pair<int,int>>> g(26);for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){if(isalpha(matrix[i][j])){g[matrix[i][j] - 'A'].emplace_back(i, j);}}}deque<tuple<int,int,int>> dq;dq.push_back({0, 0, 0});vector dist(n, vector<int>(m, INT_MAX));dist[0][0] = 0;while(dq.size()){auto [d, x, y] = dq.front(); dq.pop_front();if(x == n - 1 && y == m - 1) return d;if(d != dist[x][y]) continue;if(isalpha(matrix[x][y])){int i = matrix[x][y] - 'A';for(auto [xi, yi] : g[i]){if(dist[xi][yi] > d){dist[xi][yi] = d;dq.push_front({d, xi, yi});}}g[i].resize(0);}for(int i = 0; i < 4; i++){int xi = x + dirs[i][0], yi = y + dirs[i][1];if(xi < 0 || xi >= n || yi < 0 || yi >= m || matrix[xi][yi] == '#' || dist[xi][yi] <= d + 1)continue;dist[xi][yi] = d + 1;dq.push_back({d + 1, xi, yi});}}return -1;}
};
四、包含给定路径的最小带权子树 II
本题要求查询三个结点能够互相到达的最小权重。
思路:
-
两个结点之间能互相到达的最小权重,即两个结点的最短路径,如何求解?假设这两个结点为
A、B,它们的最近公共祖先为fa,则dist(A,B) = dist(A,root) + dist(B,root) - 2*dist(fa, root),其中 dist(x,y) 表示 x 到 y 的距离,而我们很容易得出每个结点到根节点的距离 -
如果是三个结点呢?

显然三点之间的最小权重等于dist(A,B,C) = [dist(A,B) + dist(B,C) + dist(C, A)] / 2 -
如何求解两个节点的最近公共祖先(LCA)?用树上倍增算法,能在
O(logn)的时间内计算出来
代码如下
// C++
class LcaBinaryLifting{vector<int> dist, depth;vector<vector<int>> pa;
public:LcaBinaryLifting(vector<vector<int>>& edges){int n = edges.size() + 1;int m = bit_width((unsigned) n);vector<vector<pair<int,int>>> g(n);for(auto & e : edges){g[e[0]].emplace_back(e[1], e[2]);g[e[1]].emplace_back(e[0], e[2]);}depth.resize(n);dist.resize(n);pa.resize(n, vector<int>(m, -1));auto dfs = [&](this auto && dfs, int x, int fa, int s, int d)->void{dist[x] = s;pa[x][0] = fa;depth[x] = d;for(auto [y, w] : g[x]){if(y != fa){dfs(y, x, w + s, d + 1);}}};dfs(0, -1, 0, 0);for(int j = 1; j < m; j++){for(int i = 0; i < n; i++){if(pa[i][j-1] != -1){pa[i][j] = pa[pa[i][j-1]][j-1];}}}}int getLCA(int a, int b){if(depth[a] < depth[b]){swap(a, b);}for(int k = depth[a] - depth[b]; k; k &= k - 1){a = pa[a][countr_zero((unsigned)k)];}if(a == b) return a;// 处于同一个深度for(int j = pa[a].size() - 1; j >= 0; j--){if(pa[a][j] != pa[b][j]){a = pa[a][j];b = pa[b][j];}}return pa[a][0];}int getDist(int a, int b){int c = getLCA(a, b);return dist[a] + dist[b] - dist[c] * 2;}
};
class Solution {
public:vector<int> minimumWeight(vector<vector<int>>& edges, vector<vector<int>>& queries) {LcaBinaryLifting g(edges);vector<int> ans(queries.size());for(int i = 0; i < queries.size(); i++){int a = queries[i][0], b = queries[i][1], c = queries[i][2];ans[i] = (g.getDist(a, b) + g.getDist(b, c) + g.getDist(c, a)) / 2;}return ans;}
};
# Python
class LcaBinaryLifting:def __init__(self, edges: List[List[int]]):n = len(edges) + 1m = n.bit_length()g = [[] for _ in range(n)]for x, y, w in edges:g[x].append((y, w))g[y].append((x, w))depth = [0] * ndis = [0] * npa = [[-1] * m for _ in range(n)]def dfs(x:int, fa:int)->int:pa[x][0] = fafor y, w in g[x]:if y != fa:depth[y] = depth[x] + 1dis[y] = dis[x] + wdfs(y, x)dfs(0, -1)for j in range(m - 1):for i in range(n):if pa[i][j] != -1:pa[i][j+1] = pa[pa[i][j]][j]self.depth = depthself.dis = disself.pa = padef get_kth_ancestor(self, node:int, k:int)->int:for i in range(k.bit_length()):if k >> i & 1:node = self.pa[node][i]return nodedef get_lca(self, x:int, y:int)->int:if self.depth[x] > self.depth[y]:x, y = y, xy = self.get_kth_ancestor(y, self.depth[y] - self.depth[x])if x == y:return xfor i in range(len(self.pa[x]) - 1, -1, -1):px, py = self.pa[x][i], self.pa[y][i]if px != py:x, y = py, pxreturn self.pa[x][0]def get_dis(self, x:int, y:int)->int:return self.dis[x] + self.dis[y] - 2 * self.dis[self.get_lca(x, y)]
class Solution:def minimumWeight(self, edges: List[List[int]], queries: List[List[int]]) -> List[int]:g = LcaBinaryLifting(edges)ans = []for a, b, c in queries:ans.append((g.get_dis(a, b) + g.get_dis(a, c) + g.get_dis(b, c))//2)return ans
相关文章:

LeetCode --- 450周赛
题目列表 3550. 数位和等于下标的最小下标 3551. 数位和排序需要的最小交换次数 3552. 网格传送门旅游 3553. 包含给定路径的最小带权子树 II 一、数位和等于下标的最小下标 直接模拟计算数位和即可,代码如下 // C class Solution { public:int smallestIndex(ve…...

SpringBoot中消息转换器的选择
SpringBoot返回xml-CSDN博客 是返回JSON 还是XML 是由内容协商机制确认的,SpringBoot为了开发便利性,如果我没有该消息转换器,默认就返回了JSON,如果需要XML那么,引入 <dependency><groupId>com.fasterxml.jackson.dataformat</groupId><artifactId>…...
前端初学者入门指南:HTML5与CSS3核心知识详解)
(初级)前端初学者入门指南:HTML5与CSS3核心知识详解
对于前端初学者来说,掌握HTML5和CSS3的基础知识是构建现代化网页的第一步。本文将围绕语义化标签、多媒体嵌入、盒模型、Flexbox布局和Grid布局五大核心知识点展开,通过代码示例和详细解析帮助大家快速上手。 一、HTML5:从结构到交互的革新 …...

基于点标注的弱监督目标检测方法研究
摘要 在计算机视觉领域,目标检测需要大量精准标注数据,但人工标注成本高昂。弱监督目标检测通过低成本标注训练模型,成为近年研究热点。本文提出一种基于点标注的弱监督目标检测算法,仅需在图像中物体中心点标注,即可高…...

【RichTextEditor】 【分析2】RichTextEditor设置文字内容背景色
【RichTextEditor】 【分析2】RichTextEditor设置文字内容背景色 都说AI Coder的Cursor很牛,也付费用了, 但这个背景色,搞了一天也没改过来。 最后,让它分析该控件的层次结构及文本内容显示的位置。 然后,搞定&#…...

超越OpenAI CodeX的软件工程智能体:Jules
目前AI编码代理(coding agent)领域正迅速崛起,Google推出了一款名为Jules的非同步编码代理(asynchronous coding agent),主要针对专业开发者,与传统在开发环境中直接辅助编码的Cursor或Windsurf…...

Qt实战教程:设计并实现一个结构清晰、功能完整的桌面应用
概述 本文以文本编辑器项目作为示例,文本编辑器是一个非常适合新手入门的经典项目。它具备了桌面应用开发中的核心要素: 窗口管理菜单栏和工具栏文件操作(打开、保存)多文档支持(可选)国际化支持(多语言)插件系统(进阶扩展)通过这个项目,你将学习到如何使用Qt进行桌…...

轻量化MEC终端 特点
MEC(多接入边缘计算)解决方案通过将计算能力下沉至网络边缘,结合5G网络特性,已在多个行业实现低延迟、高可靠、高安全的应用部署。以下从技术架构、核心优势及典型场景三方面进行总结: 一、技术架构 分层设计 MEC架…...

NIST提出新型安全指标:识别潜在被利用漏洞
美国国家标准与技术研究院(NIST)近日公布了一项突破性的安全指标,旨在评估哪些软件漏洞可能已被利用——即使相关组织尚未察觉。 这项由前NIST专家Peter Mell和网络安全与基础设施安全局(CISA)Jonathan Spring共同完成…...

List介绍
什么是List 在集合框架中,List是一个接口,继承自Collection Collection也是一个接口,该接口中规范了后序容器中常用的一些方法 Iterable也是一个接口,表示实现该接口的类是可以逐个元素进行遍历的,具体如下࿱…...

正则表达式全解:一文学会正则表达式【附在线正则表达式练习网站】
1.正则表达式的作用 案例演示 先给大家看一个例子,在以下文本中存储了一些职位信息: Python3 高级开发工程师 上海互教教育科技有限公司上海-浦东新区2万/月02-18满员 测试开发工程师(C++/python) 上海墨鹍数码科技有限公司上海-浦东新区2.5万/每月02-18未满员 Python3 …...

Nginx-详解(二)
nginx 常见模块 第三方模块是对nginx 的功能扩展,第三方模块需要在编译安装nginx 的时候使用参数-- add-modulePATH指定路径添加,有的模块是由公司的开发人员针对业务需求定制 开发的,有的模块是开源爱好者开发好之后上传到github进行开源的…...

解决 IntelliJ IDEA 配置文件中文被转义问题
在使用 IntelliJ IDEA 进行开发时,我们经常需要编辑各种配置文件(如 .properties、.xml、.json 等)。然而,许多开发者都遇到过这样的困扰:配置文件中的中文内容被自动转义成了 Unicode 编码,显示为类似 \u4…...

MCP、MCPHub、A2A、AG-UI概述
MCP Model Context Protocol,模型上下文协议,Anthropic于2024年开源的标准协议,旨在统一AI模型与数据源的交互方式,提升数据访问的便捷性和可靠性,提供标准化的工具调用、资源管理和提示词功能。 MCP的基本定义&…...
)
计算机视觉与深度学习 | Python实现CEEMDAN-ISOS-VMD-GRU-ARIMA时间序列预测(完整源码和数据)
以下是结合CEEMDAN、ISOS-VMD、GRU和ARIMA的时间序列预测的Python完整实现方案。本方案包含完整的代码、数据生成逻辑和实现细节说明。 完整代码实现 import numpy as np import pandas as pd from PyEMD import CEEMDAN from vmdpy import VMD from scipy.optimize import di…...

[Linux]磁盘分区及swap交换空间
linux磁盘分区 计算机容量单位:一般用B,KB,MB,GB,TB,PB,EB,ZB,YB,BB来表示。 它们之间的关系是: 1KB (Kilobyte 千字节)1024B, 1MB (Megabyte 兆…...

JAVA面向对象——对象和类的基本语法
JAVA面向对象——对象和类的基本语法 一、面向对象编程基础 1. 程序中的数据存储方式 基本类型:变量(如 int max 15;)。数据结构:数组(一维/二维)、对象(特殊数据结构,用于存储复…...

Linux常见指令合集+知识点
Linux有一条设计理念:Linux中一切皆文件;这样的设计理念让Linux可以用一种统一的方式对Linux中的不同文件/设备进行管理;(也就是键盘、显示器等在Linux中也算文件) 文件内容属性,指令一般都是对文件进行操…...

nginx 基于IP和用户的访问
nginx的下载 yum install nginx.x86_64 -y 启动服务 systemctl enable --now nginx.service 查看服务目录 [rootwebserver ~]# rpm -ql nginx /usr/bin/nginx-upgrade /usr/lib/systemd/system/nginx.service /usr/share/man/man3/nginx.3pm.gz /usr/share/man/man8/nginx…...

【Linux】系统程序−进度条
文章目录 一、准备知识1.回车与换行1.1 回车1.2 换行 2. 行缓冲区3. 倒计时程序 二、进度条程序1. 版本1 一、准备知识 在讲解进度条之前,先讲解几个概念 1.回车与换行 1.1 回车 回车:\r 作用:将光标移动到当前行的行首(水平回…...

Axure应用交互设计:动态面板嵌套实现超强体验感菜单表头
亲爱的小伙伴,在您浏览之前,烦请关注一下,在此深表感谢!如有帮助请订阅专栏! Axure产品经理精品视频课已登录CSDN可点击学习https://edu.csdn.net/course/detail/40420 课程主题:动态面板嵌套 主要内容:利用动态面板多层嵌套实现菜单表头 应用场景:广泛应用于表单表…...
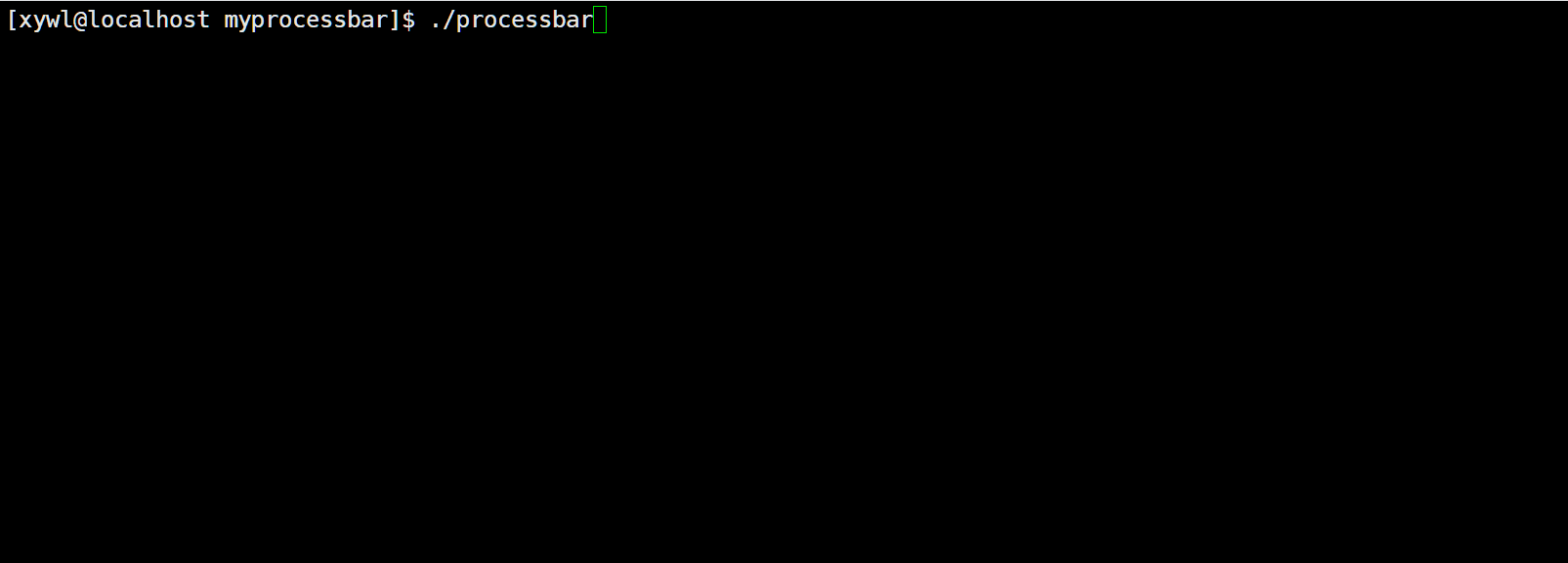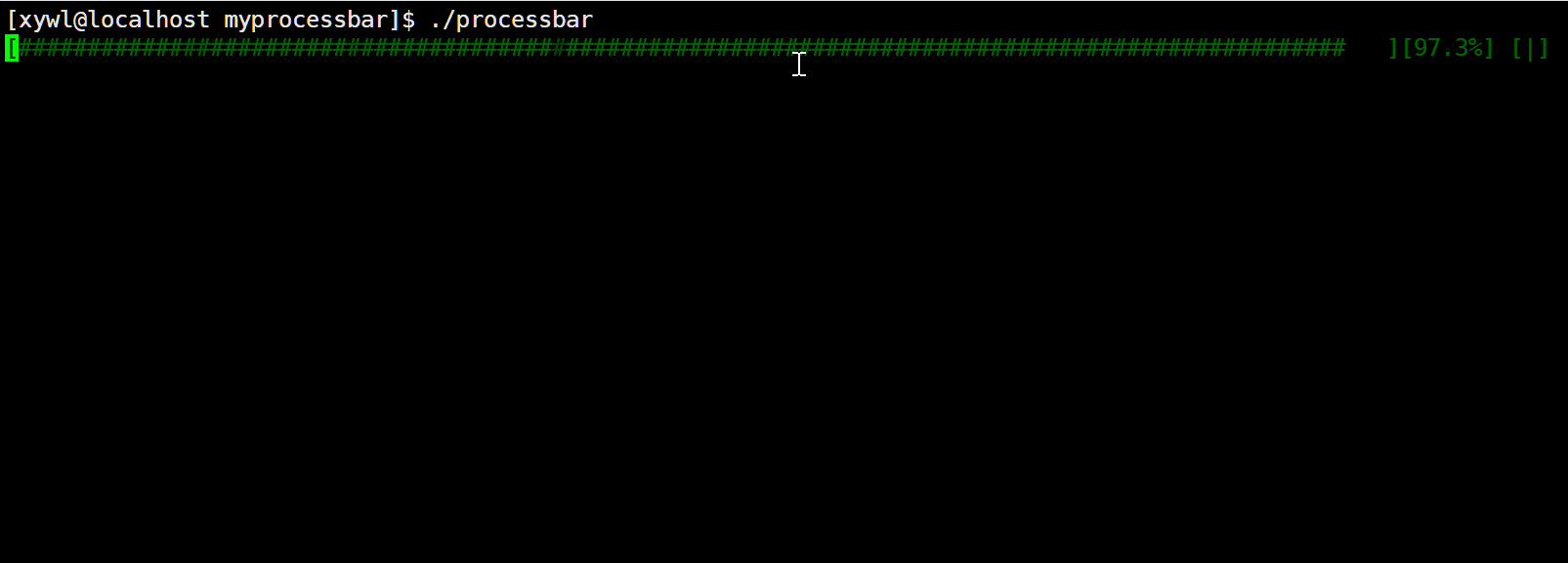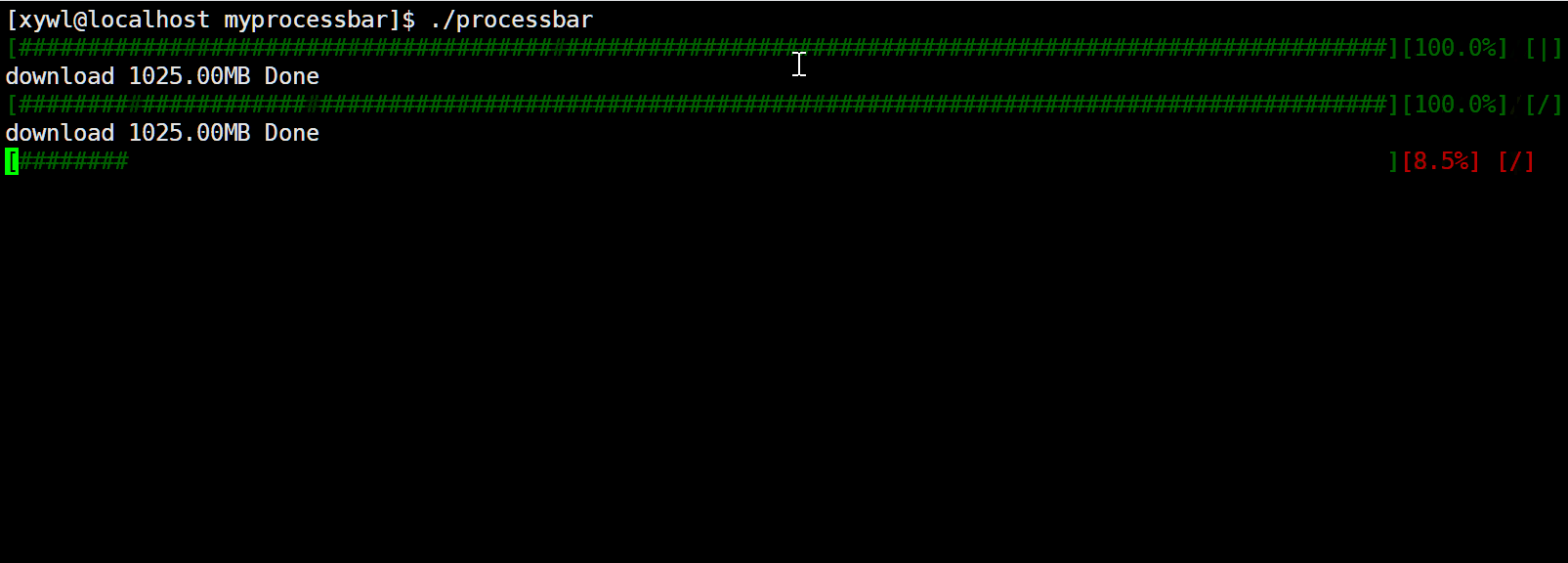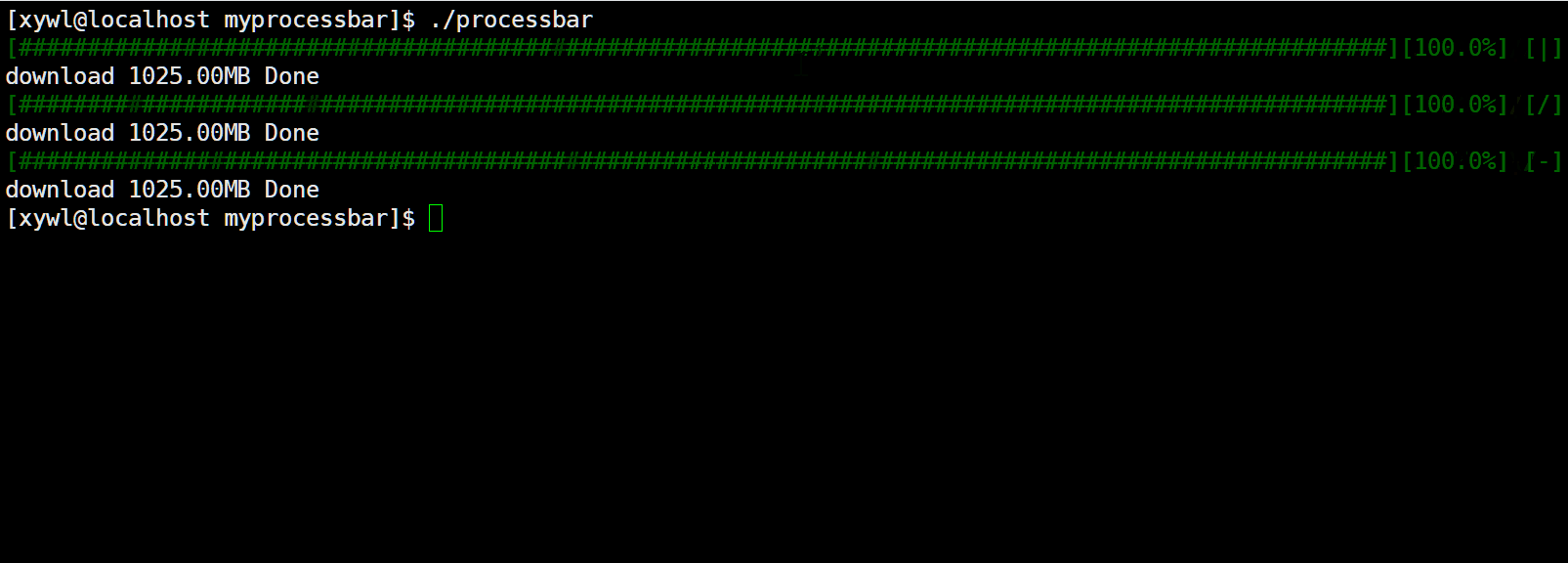
Linux(6)——第一个小程序(进度条)
目录 一、行缓冲区的概念 二、\r与\n 三、进度条代码书写与展示 1.如何表示进度条是在加载的 2.整体框架 3.书写 3.1makefile: 3.2process.h: 3.3process.c: 3.4main.c: 3.5美化 一、行缓冲区的概念 首先,我们来见一见行缓冲区,…...

CentOS:搭建国内软件repository,以实现自动yum网络安装
centosgit仓库_寂寞沙冷州的技术博客_51CTO博客 yum 很慢 centos yum安装慢_mob64ca1417b0c6的技术博客_51CTO博客 yum配置,文件,命令详解-CSDN博客 yum仓库简介_yum库是什么-CSDN博客 rootwww:/etc/yum.repos.d# pwd /etc/yum.repos.d ###创建下面这个.…...

[Git] 认识 Git 的三大区域 文件的修改和提交
文章目录 认识 Git 的三大区域:工作区、暂存区、版本库工作区、暂存区、版本库的关系流程图解 (概念) 将文件添加到仓库进行管理:git add 和 git commit场景一:第一次添加文件到仓库查看提交历史:git log(进阶理解&…...

RISC-V 开发板 MUSE Pi Pro USB 测试(3.0 U盘,2.0 UVC摄像头)
视频讲解: RISC-V 开发板 MUSE Pi Pro USB 测试(3.0 U盘,2.0 UVC摄像头) 总共开发板有4个USB的A口,1个USB的TypeC口,我们插上两个USB3.0的U盘和一个USB2.0的UVC摄像头来进行测试 lsusb -tv 可以看到有3个US…...

【520 特辑】用 HTML/CSS/JavaScript 打造浪漫炫酷的表白网页
一、前言 在 520 这个充满爱意的日子里,程序员该如何用代码表达浪漫?本文将分享一个结合动画特效与交互设计的 520 表白网页案例,通过 HTML/CSS/JavaScript 实现动态爱心、渐变背景、浮动文字等炫酷效果,手把手教你用技术传递心意…...

小米2025年校招笔试真题手撕(二)
一、题目 给一个长度为n的序列和一个整数x,每次操作可以选择序列中的一个元素,将其从序列中删去,或者将其值加一。 问至少操作多少次,可以使操作后的序列(可以为空)中数字之和是x的倍数。 输入描述&#…...

弱网服务器群到底有什么用
在当今数字化的时代,大家都在追求高速、稳定的网络体验,但你是否想过,弱网服务器群其实也有着不可小觑的作用。让我们来聊聊什么是弱网服务器群。简单来说,它是一组在网络条件相对较差情况下运行的服务器集合。 弱网服务器群组是一…...

部署Gitlab-CE with Docker私有云环境
应用环境 Ubuntu 20.04.6 LTS (GNU/Linux 5.15.0-139-generic x86_64) Docker version 28.1.1, build 4eba377 文章目录 拉取容器镜像生成Run脚本参数解读实例脚本环境配置管理员密码遗忘服务邮箱配置邮件测试 运维问题集锦(1) 端口映射关系(2) 服务日志(3) 分支受保护 项目操作…...
拉普拉斯高斯(LoG)滤波器掩模的注意事项
目录 问题: 解答: 一、高斯函数归一化:消除幅度偏差 1. 归一化的定义 2. 为何必须归一化? 二、拉普拉斯系数和为零:抑制直流项干扰 1. 拉普拉斯算子的特性 2. 系数和不为零的后果 三、直流项如何影响零交叉点&…...
