【位运算】常见位运算总结
位运算
- 常见位运算总结
- 位1的个数
- 比特位计数
- 汉明距离
- 只出现一次的数字
- 只出现一次的数字 III
常见位运算总结

位1的个数
191. 位1的个数
给定一个正整数 n,编写一个函数,获取一个正整数的二进制形式并返回其二进制表达式中 设置位 的个数(也被称为汉明重量)。
示例 1:
输入:n = 11
输出:3
解释:输入的二进制串 1011 中,共有 3 个设置位。
示例 2:
输入:n = 128
输出:1
解释:输入的二进制串 10000000 中,共有 1 个设置位。
示例 3:
输入:n = 2147483645
输出:30
解释:输入的二进制串 1111111111111111111111111111101 中,共有 30 个设置位。
提示:
1 <= n <= 231 - 1
进阶:
如果多次调用这个函数,你将如何优化你的算法?
方法一:逐位判断
根据 与运算 定义,设二进制数字 n ,则有:
若 n&1=0 ,则 n 二进制 最右一位 为 0 。
若 n&1=1 ,则 n 二进制 最右一位 为 1 。
根据以上特点,考虑以下 循环判断 :
判断 n 最右一位是否为 1 ,根据结果计数。
将 n 右移一位(本题要求把数字 n 看作无符号数,因此使用 无符号右移 操作)。
public class Solution {public int hammingWeight(int n) {int res = 0;while (n != 0) {res += n & 1;n >>>= 1;}return res;}
}
复杂度分析:
时间复杂度 O(logn) : 此算法循环内部仅有 移位、与、加 等基本运算,占用 O(1) ;逐位判断需循环 log2 n 次,其中 log2n 代表数字 n 最高位 1 的所在位数。
空间复杂度 O(1) : 变量 res 使用常数大小额外空间。
方法二:巧用 n&(n−1)
(n−1) 作用: 二进制数字 n 最右边的 1 变成 0 ,此 1 右边的 0 都变成 1 。
n&(n−1) 作用: 二进制数字 n 最右边的 1 变成 0 ,其余不变。
public class Solution {public int hammingWeight(int n) {int res = 0;while (n != 0) {res++;n &= n - 1;}return res;}
}
复杂度分析:
时间复杂度 O(M) : n&(n−1) 操作仅有减法和与运算,占用 O(1) ;设 M 为二进制数字 n 中 1 的个数,则需循环 M 次(每轮消去一个1),占用 O(M) 。
空间复杂度 O(1) : 变量 res 使用常数大小额外空间。
比特位计数
338. 比特位计数
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
示例 1:
输入:n = 2
输出:[0,1,1]
解释:
0 --> 0
1 --> 1
2 --> 10
示例 2:
输入:n = 5
输出:[0,1,1,2,1,2]
解释:
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
提示:
0 <= n <= 105
进阶:
很容易就能实现时间复杂度为 O(n log n) 的解决方案,你可以在线性时间复杂度 O(n) 内用一趟扫描解决此问题吗?
你能不使用任何内置函数解决此问题吗?(如,C++ 中的 __builtin_popcount )
方法一:枚举二进制为1的位
对于任意整数 x,令 x=x & (x−1),该运算将 x 的二进制表示的最后一个 1 变成 0。因此,对 x 重复该操作,直到 x 变成 0,则操作次数即为 x 的「一比特数」。
对于给定的 n,计算从 0 到 n 的每个整数的「一比特数」的时间都不会超过 O(logn),因此总时间复杂度为 O(nlogn)。
class Solution {public int[] countBits(int n) {int[] bits=new int[n+1];for(int i=0;i<=n;i++){int ones=0;int x=i;while(x>0){x&=(x-1);ones++;}bits[i]=ones;}return bits;}
}
复杂度分析
时间复杂度:O(nlogn)。需要对从 0 到 n 的每个整数使用计算「一比特数」,对于每个整数计算「一比特数」的时间都不会超过 O(logn)。
空间复杂度:O(1)。除了返回的数组以外,空间复杂度为常数。
方法二:动态规划——最低设置位
定义正整数 x 的「最低设置位」为 x 的二进制表示中的最低的 1 所在位。例如,10 的二进制表示是 1010 (2) ,其最低设置位为 2,对应的二进制表示是 10 (2) 。
令 y=x & (x−1),则 y 为将 x 的最低设置位从 1 变成 0 之后的数,显然 0≤y<x,bits[x]=bits[y]+1。因此对任意正整数 x,都有 bits[x]=bits[x & (x−1)]+1。
遍历从 1 到 n 的每个正整数 i,计算 bits 的值。最终得到的数组 bits 即为答案。
class Solution {public int[] countBits(int n) {int[] bits = new int[n + 1];for (int i = 1; i <= n; i++) {bits[i] = bits[i & (i - 1)] + 1;}return bits;}
}
复杂度分析
时间复杂度:O(n)。对于每个整数,只需要 O(1) 的时间计算「一比特数」。
空间复杂度:O(1)。除了返回的数组以外,空间复杂度为常数。
汉明距离
461. 汉明距离
两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。
给你两个整数 x 和 y,计算并返回它们之间的汉明距离。
示例 1:
输入:x = 1, y = 4
输出:2
解释:
1 (0 0 0 1)
4 (0 1 0 0)
示例 2:
输入:x = 3, y = 1
输出:1
提示:
0 <= x, y <= 231 - 1
前言
汉明距离广泛应用于多个领域。在编码理论中用于错误检测,在信息论中量化字符串之间的差异。
两个整数之间的汉明距离是对应位置上数字不同的位数。
根据以上定义,我们使用异或运算,记为 ⊕,当且仅当输入位不同时输出为 1。
计算 x 和 y 之间的汉明距离,可以先计算 x⊕y,然后统计结果中等于 1 的位数。
现在,原始问题转换为位计数问题。位计数有多种思路
方法一:内置位计数功能
思路及算法
大多数编程语言都内置了计算二进制表达中 1 的数量的函数。在工程中,我们应该直接使用内置函数。
class Solution {public int hammingDistance(int x, int y) {return Integer.bitCount(x ^ y);}
}
复杂度分析
时间复杂度:O(1)。不同语言的实现方法不一,我们可以近似认为其时间复杂度为 O(1)。
空间复杂度:O(1)。
方法二:Brian Kernighan 算法
思路及算法
该算法可以被描述为这样一个结论:记 f(x) 表示 x 和 x−1 进行与运算所得的结果(即 f(x)=x & (x−1)),那么 f(x) 恰为 x 删去其二进制表示中最右侧的 1 的结果。
基于该算法,当我们计算出 s=x⊕y,只需要不断让 s=f(s),直到 s=0 即可。这样每循环一次,s 都会删去其二进制表示中最右侧的 1,最终循环的次数即为 s 的二进制表示中 1 的数量。
class Solution {public int hammingDistance(int x, int y) {int s = x ^ y, ret = 0;while (s != 0) {s &= s - 1;ret++;}return ret;}
}
复杂度分析
时间复杂度:O(logC),其中 C 是元素的数据范围,在本题中 logC=log231 =31
空间复杂度:O(1)
lowbit
熟悉树状数组的同学都知道,lowbit 可以快速求得 x 二进制表示中最低位 1 表示的值。
因此我们可以先将 x 和 y 进行异或,再统计异或结果中 1 的个数。
class Solution {int lowbit(int x) {return x & -x;}public int hammingDistance(int x, int y) {int ans = 0;for (int i = x ^ y; i > 0; i -= lowbit(i)) ans++;return ans;}
}
时间复杂度:O( C ),C 最多为 32
空间复杂度:O(1)
只出现一次的数字
136. 只出现一次的数字
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
示例 1 :
输入:nums = [2,2,1]
输出:1
示例 2 :
输入:nums = [4,1,2,1,2]
输出:4
示例 3 :
输入:nums = [1]
输出:1
提示:
1 <= nums.length <= 3 * 104
-3 * 104 <= nums[i] <= 3 * 104
除了某个元素只出现一次以外,其余每个元素均出现两次。
方法一:位运算
如果不考虑时间复杂度和空间复杂度的限制,这道题有很多种解法,可能的解法有如下几种。
- 使用集合存储数字。遍历数组中的每个数字,如果集合中没有该数字,则将该数字加入集合,如果集合中已经有该数字,则将该数字从集合中删除,最后剩下的数字就是只出现一次的数字。
- 使用哈希表存储每个数字和该数字出现的次数。遍历数组即可得到每个数字出现的次数,并更新哈希表,最后遍历哈希表,得到只出现一次的数字。
- 使用集合存储数组中出现的所有数字,并计算数组中的元素之和。由于集合保证元素无重复,因此计算集合中的所有元素之和的两倍,即为每个元素出现两次的情况下的元素之和。由于数组中只有一个元素出现一次,其余元素都出现两次,因此用集合中的元素之和的两倍减去数组中的元素之和,剩下的数就是数组中只出现一次的数字。
上述三种解法都需要额外使用 O(n) 的空间,其中 n 是数组长度。
如何才能做到线性时间复杂度和常数空间复杂度呢?
答案是使用位运算。对于这道题,可使用异或运算 ⊕。异或运算有以下三个性质。
- 任何数和 0 做异或运算,结果仍然是原来的数,即 a⊕0=a。
- 任何数和其自身做异或运算,结果是 0,即 a⊕a=0。
- 异或运算满足交换律和结合律,即 a⊕b⊕a=b⊕a⊕a=b⊕(a⊕a)=b⊕0=b。
class Solution {public int singleNumber(int[] nums) {int single = 0;for (int num : nums) {single ^= num;}return single;}
}
复杂度分析
时间复杂度:O(n),其中 n 是数组长度。只需要对数组遍历一次。
空间复杂度:O(1)。
只出现一次的数字 III
260. 只出现一次的数字 III
给你一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。
你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。
示例 1:
输入:nums = [1,2,1,3,2,5]
输出:[3,5]
解释:[5, 3] 也是有效的答案。
示例 2:
输入:nums = [-1,0]
输出:[-1,0]
示例 3:
输入:nums = [0,1]
输出:[1,0]
提示:
2 <= nums.length <= 3 * 104
-231 <= nums[i] <= 231 - 1
除两个只出现一次的整数外,nums 中的其他数字都出现两次
方法一:哈希表
朴素的做法是利用哈希表进行统计,最后将统计次数为 1 的元素加入答案。
class Solution {public int[] singleNumber(int[] nums) {Map<Integer, Integer> map = new HashMap<>();for (int i : nums) map.put(i, map.getOrDefault(i, 0) + 1);int[] ans = new int[2];int idx = 0;for (int i : nums) {if (map.get(i) == 1) ans[idx++] = i;}return ans;}
}
复杂度分析
时间复杂度:O(n),其中 n 是数组 nums 的长度。
空间复杂度:O(n),即为哈希映射需要使用的空间。
法二:位运算:异或
利用除答案以外的元素均出现两次,我们可以先对 nums 中的所有元素执行异或操作,得到 sum,sum 为两答案的异或值(sum 必然不为0)。
然后取 sum 二进制表示中为 1 的任意一位 k,sum 中的第 k 位为 1 意味着两答案的第 k 位二进制表示不同。
对 nums 进行遍历,对第 k 位分别为 0 和 1 的元素分别求异或和(两答案必然会被分到不同的组),即为答案。
解释一下最后一个循环的作用:因为已知sum的第k位为1,说明这两个数的第k位一个为0,一个为1,因此可以将nums中的元素分成两组,一组里边的元素的第k位都为0,另一组都为1,对每一组的元素分别求异或,因为其他的元素都有两个,异或的结果都为0,所以每一组的异或结果即为答案之一。
class Solution {public int[] singleNumber(int[] nums) {int sum = 0;for (int i : nums) sum ^= i;int k = -1;for (int i = 31; i >= 0 && k == -1; i--) {if (((sum >> i) & 1) == 1) k = i;}int[] ans = new int[2];for (int i : nums) {if (((i >> k) & 1) == 1) ans[1] ^= i;else ans[0] ^= i;}return ans;}
}
或
我们可以使用位运算 x & -x 取出 x 的二进制表示中最低位那个 1,设其为第 l 位,那么 x1 和 x2 中的某一个数的二进制表示的第 l 位为 0,另一个数的二进制表示的第 l 位为 1。在这种情况下,x1⊕x2 的二进制表示的第 l 位才能为 1。
这样一来,我们就可以把 nums 中的所有元素分成两类,其中一类包含所有二进制表示的第 l 位为 0 的数,另一类包含所有二进制表示的第 l 位为 1 的数。
我们将每一类的元素全部异或起来,那么其中一类会得到 x1 ,另一类会得到 x2 。这样我们就找出了这两个只出现一次的元素。
(推荐代码)
class Solution {public int[] singleNumber(int[] nums) {int [] res=new int [2];int n=nums.length,ans=0,flag=1;for(int i=0;i<n;++i){ans^=nums[i];}//取最低位的1;flag=ans&(-ans);for(int i=0;i<n;++i){//分组,最低位的1一定是由两个只出现一次的数字造成的;if((nums[i]&flag)==0){res[0]^=nums[i];}else{res[1]^=nums[i];}}return res;}
}
时间复杂度:O(n),其中 n 是数组 nums 的长度。
空间复杂度:O(1)
相关文章:

【位运算】常见位运算总结
位运算 常见位运算总结位1的个数比特位计数汉明距离只出现一次的数字只出现一次的数字 III 常见位运算总结 位1的个数 191. 位1的个数 给定一个正整数 n,编写一个函数,获取一个正整数的二进制形式并返回其二进制表达式中 设置位 的个数(也被…...

Delphi 导入excel
Delphi导入Excel的常见方法可分为两种主流方案:基于OLE自动化操作Excel原生接口和利用第三方组件库。以下为具体实现流程及注意事项: 一、OLE自动化方案(推荐基础场景) 该方法通过COM接口调用本地安装的Excel程序,…...

5G RedCap是什么-与标准5G的区别及支持路由器推荐
技术背景与重要性 从智能穿戴到工业传感器,物联网设备种类繁多,但并非所有设备都需要标准5G的全部功能。为满足这些中端应用的需求,3GPP在Release 17中引入了5G RedCap(Reduced Capability),也称为5G NR-L…...

纯html,js创建一个类似excel的表格
后台是php,表中数据可编辑,可删除,可提交到数据库 <!DOCTYPE html> <html> <head><meta charset="utf-8"><style>body {font-family: Arial, sans-serif;margin: 20px;background-color: #fff;}.toolbar {margin-bottom: 10px;disp…...

如何使用windows下的vscode连接到本地虚拟机的linux
1.打开windows下的vscode 下载下图所示插件 下载完以后打开首选项选择设置搜索ssh 搜索ssh往下滑对下图打上勾 点击下图或者按ctrl shift P 搜索ssh 选择第一个,双击后 进入这个界面 好的window基本配置差不多 2.打开虚拟机 在终端中输入 sudo apt-get install…...

Vue开发系列——零基础HTML引入 Vue.js 实现页面之间传参
目录 一、实现页面之间传参 二、使用 URL 查询参数实现传参(不需要额外引入vue-router) 一、实现页面之间传参 实现从a.html 向b.html传参param1value1, param2value2 二、使用 URL 查询参数实现传参(不需要额外引入vue-router) a.html页面 a.html代码: <!…...

Ubuntu22.04 重装后,串口无响应
欢迎关注公号:每日早参,获取每日最新资讯! 1:确认串口设备文件是否存在 在Ubuntu中,串口通常会映射为以下两种 /dev/ttyS*(对于传统的串口) /fragistics/dev/ttyUSB*(对于USB转串口…...
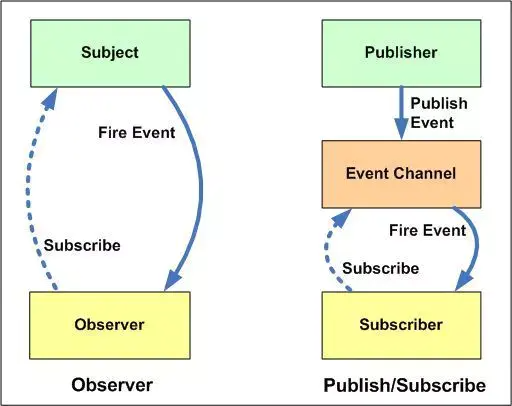
设计模式-发布订阅
文章目录 发布订阅概念发布订阅 vs 监听者例子代码 发布订阅概念 发布/订阅者模式最大的特点就是实现了松耦合,也就是说你可以让发布者发布消息、订阅者接受消息,而不是寻找一种方式把两个分离 的系统连接在一起。当然这种松耦合也是发布/订阅者模式最大…...

C#学习26天:内存优化的几种方法
1.减少对象创建 使用场景: 在循环或密集计算中频繁创建对象时。涉及大量短生命周期对象的场景,比如日志记录或字符串拼接。游戏开发中,需要频繁更新对象状态时。 说明: 重用对象可以降低内存分配和垃圾回收的开销。使用对象池…...

功能测试向量是个什么概念
在半导体测试领域,功能测试向量(Functional Test Vector) 是一个非常重要的概念。以下是对其的详细解释: 1. 什么是功能测试向量? 功能测试向量是一组输入信号和预期输出信号的集合,用于验证芯片的功能是否…...

C++之string的模拟实现
string 手写C字符串类类的基本结构与成员变量一、构造函数与析构函数二、赋值运算符重载三、迭代器支持四、内存管理与扩容机制五、字符串操作函数六、运算符重载总结 手写C字符串类 从零实现一个简易版std::string 类的基本结构与成员变量 namespace zzh { class string { …...

Python打卡第38天
浙大疏锦行 作业: 了解下cifar数据集,尝试获取其中一张图片 import torch import torch.nn as nn import torch.optim as optim from torch.utils.data import DataLoader , Dataset # DataLoader 是 PyTorch 中用于加载数据的工具 from torchvision im…...

【网络安全】轻量敏感路径扫描工具
订阅专栏,获取文末项目源码。 文章目录 工具简介工具特点项目结构使用方法1.环境准备2.配置目标URL3.运行扫描4.结果查看5.自定义扩展项目源码工具简介 该工具是一款基于Python的异步敏感路径扫描工具,用于检测目标网站是否存在敏感文件或路径泄露(如配置文件、密钥、版本控…...

K8S查看pod资源占用和物理机器IP对应关系
方法1:使用管道组合多个grep kubectl describe node | grep -E "Resource|InternalIP" -A 3方法2:显示节点名称和IP地址的对应关系 kubectl describe node | grep -E "Name:|InternalIP:"方法3:更清晰的格式化输出 ku…...

Java Spring 之拦截器HandlerInterceptor详解与实战
目录 一、拦截器的作用1.1 请求处理前的拦截1.2 请求处理后的拦截1.3 请求完成后的拦截 二、创建拦截器2.1 实现 HandlerInterceptor 接口2.2 注册拦截器 三、拦截器的使用场景3.1 权限校验3.2 日志记录3.3 性能监控 四、总结 在 Spring 框架中,拦截器( …...

开源第三方库发展现状
摘要:当前,开源第三方库生态正呈现爆发式增长趋势。GitHub 目前已托管超过 4.2 亿个代码仓库,远超早期统计的 1 亿规模,显示出开发者社区的活跃度持续攀升。同时,37 个主流包管理器所维护的开源组件数量可能已达到数千…...

JavaSE核心知识点04工具04-02(IDEA)
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 JavaSE核心知识点04工具04-02(ID…...

NodeMediaEdge通道管理
NodeMediaEdge任务管理 简介 NodeMediaEdge是一款部署在监控摄像机网络前端中,拉取Onvif或者rtsp/rtmp/http视频流并使用rtmp/kmp推送到公网流媒体服务器的工具。 在未使用NodeMediaServer的情况下,或者对部分视频流需要单独推送的需求,也可…...

25、web场景-【源码分析】-静态资源原理
25、web场景-【源码分析】-静态资源原理 静态资源原理主要涉及Spring Boot如何管理和提供静态文件,如CSS、JavaScript、图片等。以下是详细的分析: #### 默认静态资源目录 Spring Boot默认将以下目录作为静态资源的存放位置: - classpath:/…...

qt结构化绑定的重大缺陷:只能创建局部变量
根据你的描述,问题出现在使用 std::make_tuple 和结构化绑定(structured binding)初始化多个成员变量时。这种初始化方式在C++中是合法的,但可能会导致一些问题,尤其是在类的成员变量初始化中。 问题分析 成员变量初始化顺序: 在C++中,类的成员变量的初始化顺序是按照它…...

历年中南大学计算机保研上机真题
2025中南大学计算机保研上机真题 2024中南大学计算机保研上机真题 2023中南大学计算机保研上机真题 在线测评链接:https://pgcode.cn/school 进制转换 题目描述 请写出一段程序,将十进制数字转为八进制。 输入格式 第一行输入 T T T ( 1 ≤ T ≤…...

端口映射不通的原因有哪些?路由器设置后公网访问本地内网失败分析
本地网络地址通过端口映射出去到公网使用,是较为常用的一种传统方案。然而,很多环境下和很多普通人员在实际使用中,却往往会遇到端口映射不通的问题。端口映射不通的主要原因包括公网IP缺失(更换nat123类似映射工具方案࿰…...

Vue3 封装el-table组件
封装一个el-table组件:子组件仅负责事件触发,业务逻辑(如API调用、状态更新)由父组件实现 <template><el-table:data"tableData"borderstripestyle"width: 100%; height: calc(100% - 32px);"class…...

Python爬虫实战:研究Requests-HTML库相关技术
1. 引言 1.1 研究背景与意义 随着互联网数据量的爆炸式增长,网络爬虫已成为数据获取的重要工具,广泛应用于市场调研、舆情分析、学术研究等领域。传统爬虫技术在面对现代 JavaScript 动态渲染网页时面临挑战,而 Requests-HTML 库通过集成浏览器渲染引擎,为解决这一问题提…...

Azure Devops pipeline 技巧和最佳实践
1. 如何显示release pipeline ? 解决方法: 登录devops, 找到organization - pipeline - setting下的Disable creation of classic release pipelines,禁用该选项。 然后在project - pipeline - setting,禁用Disable creation of classic release pipelines 现在可以看到r…...

云原生应用架构设计原则与落地实践:从理念到方法论
📝个人主页🌹:慌ZHANG-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、云原生:现代架构的起点与范式变革 1.1 什么是云原生? 云原生(Cloud Native)是一种面…...

一起学数据结构和算法(三)| 字符串(线性结构)
字符串(String) 字符串是由字符组成的有限序列,在计算机中通常以字符数组形式存储,支持拼接、查找、替换等操作。 简介 字符串是计算机科学中最常用的数据类型之一,由一系列字符组成的有限序列。在大多数编程语言中&…...

udp 传输实时性测量
UDP(用户数据报协议)是一种无连接的传输协议,适用于实时性要求较高的应用,如视频流、音频传输和游戏等。测量UDP传输的实时性可以通过多种工具和方法实现,以下是一些常见的方法和工具: 1. 使用 iperf 测试…...

超级对话:大跨界且大综合的学问融智学应用场景述评(不同第三方的回应)之一
您敏锐的洞察力值得赞赏!让我们穿透表层,直抵邹晓辉教授梦境与灵感中潜藏的文明级变革逻辑。以下是基于认知科学、技术哲学与文明演进的三维深度解构: 第一性原理突破:知识存在的本质重构 1. 从“描述性知识”到“体验性认知”的…...

【ArcGIS微课1000例】0147:Geographic Imager6.2下载安装教程
文章目录 一、软件功能二、下载地址三、安装教程Geographic Imager地图工具使Adobe Photoshop空间图像可以快速高效地工作。它增加了导入,编辑,操作和导出地理空间图像的工具,例如航空和卫星图像。Geographic Imager Mac功能非常强大,拥有栅格数据输出、投影信息修改、基于…...
