【排序算法】快速排序详解--附详细流程代码
快速排序算法
介绍
快速排序(Quick Sort)是一种高效的分治排序算法,由英国计算机科学家 Tony Hoare 于 1960 年提出。它是实际应用中最常用的排序算法之一。快速排序的基本思想是:选择一个"基准"(pivot)元素,通过一次排序将待排序列分割成独立的两部分,一部分所有元素均小于基准,另一部分所有元素均大于基准,然后递归地对这两部分分别进行快速排序。分治策略的运用让快速排序在平均情况下能达到 O(nlogn) 的时间复杂度,大大优于简单排序算法的 O(n²) 性能。
算法步骤
- 从数列中选择一个元素作为"基准"(pivot),本文采用最左侧元素作为基准
- 将所有比基准值小的元素放到基准前面,所有比基准值大的元素放到基准后面(分区操作)
- 对基准左右两个子序列分别重复步骤1和2,直到子序列只有一个元素或为空

核心特性
- 分治策略:将问题分解为更小的子问题,逐步解决
- 原地排序:只需要 O(logn) 的额外空间复杂度(主要用于递归调用的栈空间)
- 时间复杂度:平均情况为 O(nlogn),最坏情况为 O(n²),最好情况为 O(nlogn)
- 不稳定性:相等元素的相对位置在排序后可能会改变
- 高效性:在实际应用中,快速排序通常是最快的排序算法之一
基础实现
接下来大家一起看下快速排序的部分主流语言实现:
代码实现
Java实现
public class QuickSort {public static void quickSort(int[] arr, int low, int high) {if (low < high) {int pivotIndex = partition(arr, low, high);quickSort(arr, low, pivotIndex - 1);quickSort(arr, pivotIndex + 1, high);}}private static int partition(int[] arr, int low, int high) {int pivot = arr[low];int i = low + 1;for (int j = low + 1; j <= high; j++) {if (arr[j] < pivot) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;i++;}}int temp = arr[low];arr[low] = arr[i - 1];arr[i - 1] = temp;return i - 1;}public static void printArray(int[] arr) {for (int i : arr) {System.out.print(i + " ");}System.out.println();}public static void main(String[] args) {int[] arr = {10, 7, 8, 9, 1, 5};System.out.println("排序前的数组:");printArray(arr);quickSort(arr, 0, arr.length - 1);System.out.println("排序后的数组:");printArray(arr);}
}注意,在上述代码里,通过:
for (int j = low + 1; j <= high; j++) {if (arr[j] < pivot) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;i++;}
}将小于基准的元素移到左侧,然后通过:
int temp = arr[low];
arr[low] = arr[i - 1];
arr[i - 1] = temp;修正基准的位置,实现基准左侧都小于基准、基准右侧大于等于基准。
优化策略
随机选择基准元素
使用最左侧元素作为基准可能会在数组已经排序或接近排序时导致最坏性能,随机选择基准可以降低这种风险:
private static int randomPartition(int[] arr, int low, int high) {int randomIndex = low + (int)(Math.random() * (high - low + 1));int temp = arr[randomIndex];arr[randomIndex] = arr[low];arr[low] = temp;return partition(arr, low, high);
}三数取中法
选择左端、中间和右端三个元素的中值作为基准,可以进一步优化快速排序:
private static int medianOfThreePartition(int[] arr, int low, int high) {int mid = low + (high - low) / 2;if (arr[mid] < arr[low])swap(arr, mid, low);if (arr[high] < arr[low])swap(arr, high, low);if (arr[high] < arr[mid])swap(arr, high, mid);swap(arr, mid, low);return partition(arr, low, high);
}优缺点
优点
- 平均情况下非常高效,时间复杂度为 O(nlogn)
- 原地排序,空间复杂度低
- 缓存友好,数据局部性好
- 适合处理大规模数据
- 在许多实际应用中表现优秀
缺点
- 最坏情况下性能退化至 O(n²),比如当数组已经排序时
- 不稳定的排序算法
- 对于小数组,快速排序可能比其他基础排序慢
- 递归实现可能导致栈溢出(可以使用迭代方式解决)
应用场景
- 需要高效排序大量数据的情况
- 作为系统库中的排序函数(如 C++ 的 std::sort、Java 的 Arrays.sort)
- 需要就地排序且对空间复杂度敏感的场景
- 需要平均情况下高性能的应用
扩展
双轴快速排序
Java 的 Arrays.sort() 使用的是双轴快速排序,它使用两个枢轴(基准),可以进一步提高性能:
public static void dualPivotQuickSort(int[] arr, int low, int high) {if (high <= low) return;if (arr[low] > arr[high]) {int temp = arr[low];arr[low] = arr[high];arr[high] = temp;}int pivot1 = arr[low];int pivot2 = arr[high];int lt = low + 1; int gt = high - 1; int i = low + 1; while (i <= gt) {if (arr[i] < pivot1) {int temp = arr[lt];arr[lt] = arr[i];arr[i] = temp;lt++;i++;} else if (arr[i] > pivot2) {int temp = arr[i];arr[i] = arr[gt];arr[gt] = temp;gt--;} else {i++;}}arr[low] = arr[lt - 1];arr[lt - 1] = pivot1;arr[high] = arr[gt + 1];arr[gt + 1] = pivot2;dualPivotQuickSort(arr, low, lt - 2);dualPivotQuickSort(arr, lt, gt);dualPivotQuickSort(arr, gt + 2, high);
}测验
这里准备了一些测试题,方便大家判断自己的掌握情况:
- 快速排序的平均时间复杂度是多少?
- 快速排序是稳定的排序算法吗?
- 使用最左侧元素作为基准的快速排序在什么情况下会出现最坏性能?
- 快速排序的空间复杂度是多少?为什么?
测验答案
- O(nlogn)。
- 不是,因为基准元素的移动可能会改变相等元素的相对位置。
- 当数组已经排序或接近排序时,每次分区只能减少一个元素,时间复杂度退化为O(n²)。
- O(logn),主要是递归调用占用的栈空间,最坏情况下为O(n)。
相关的 LeetCode 热门题目
给大家推荐一些可以用来练手的 LeetCode 题目:
- 215. 数组中的第K个最大元素 - 可以使用快速选择算法(快速排序的变体)求解,练习分区思想
- 912. 排序数组
- 75. 颜色分类 - 一个经典的荷兰国旗问题,可以使用类似快速排序的分区思想解决
来自: 快速排序 - 算法导航
相关文章:

【排序算法】快速排序详解--附详细流程代码
快速排序算法 介绍 快速排序(Quick Sort)是一种高效的分治排序算法,由英国计算机科学家 Tony Hoare 于 1960 年提出。它是实际应用中最常用的排序算法之一。快速排序的基本思想是:选择一个"基准"(pivot&am…...

Kerberos面试内容整理-会话密钥的协商与使用
在 Kerberos 认证过程中,**会话密钥(Session Key)**扮演着关键角色。会话密钥是由 KDC 临时生成并分发给通信双方用于当前会话的对称加密密钥。与用户密码这类长期密钥不同,会话密钥的生命周期很短,仅在特定的认证会话或服务访问期间有效。这种设计大幅提升了安全性:长期…...

解决各个系统报错TDengine:no taos in java.library.path问题
windows 系统解决办法 在本地上安装一个TD的Windows客户端,注意安装的客户端版本一定要和服务端TD版本完全一致。(或者将 C:\TDengine\driver\taos.dll 拷贝到 C:\Windows\System32\ 目录下) 客户端各个历史版本下载链接:TDengin…...

java helloWord java程序运行机制 用idea创建一个java项目 标识符 关键字 数据类型 字节
HelloWord public class Hello{public static void main(String[] args) {System.out.print("Hello,World!");} }java程序运行机制 用idea创建一个java项目 建立一个空项目 新建一个module 注释 标识符 关键字 标识符注意点 数据类型 public class Demo02 {public st…...

LVS-NAT 负载均衡群集
目录 简介 一、LVS 与群集技术基础 1.1 群集技术概述 1.2 负载均衡群集的分层结构 1.3 负载均衡工作模式 二、LVS 虚拟服务器核心组件与配置 2.1 LVS 内核模块与管理工具 2.2 负载调度算法解析 2.3 ipvsadm 管理工具实战 三、NFS 共享存储服务配置 3.1 NFS 服务基础…...
免费文本转语音工具体验:祈风TTS使用
简介:语音生成的另一种方式 现在很多人通过视频记录生活,表达观点。拍摄剪辑不难,配音成了常见难题。部分人对自己的声音不够自信,也有人在特定场景下不便出声。文本转语音工具可以成为解决方案。 常见的TTS(Text To…...

ipv6与p2p的关系
在PCDN(P2P内容分发网络)领域,IPv6与PCDN盒子的关系紧密且相互影响,主要体现在以下几个方面: 一、IPv6的部署推动PCDN盒子普及 地址资源充足 IPv6采用128位地址,解决了IPv4地址枯竭的问题,为PC…...

JS和TS的区别
JavaScript 与 TypeScript 的主要区别和特性对比 1. 基础定义 JavaScript 是一种动态、弱类型的编程语言,广泛应用于前端开发以及通过 Node.js 扩展到后端开发。TypeScript 则是 JavaScript 的超集,它在 JavaScript 的基础上添加了静态类型系统和其他增…...

Python实现P-PSO优化算法优化BP神经网络分类模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 随着人工智能技术的快速发展,神经网络在分类任务中展现了强大的性能。BP(Back Propagation&…...

Linux --进度条小程序更新
这里使用随机数来模拟下载量,来实现一个下载进度更新的小程序 main.c 的代码,其中downlod这个函数使用的是函数指针,如果有多个进度条函数可以传入进行多样化的格式下载显示,还需要传入一个下载总量,每次"下载以…...

JVM——回顾:JVM的起源、特性与系统构成
引入 在当今数字化时代,Java语言及其运行环境Java虚拟机(JVM)在软件开发领域占据着举足轻重的地位。从大型企业级应用到各类移动应用,JVM凭借其独特的特性和强大的功能,为开发者提供了高效且稳定的运行环境。 JVM的起…...

实现MPC钱包
多方计算(MPC,Multiparty Computation)钱包是一种利用密码学技术实现的加密货币钱包,它允许多个参与者共同生成和管理钱包的私钥,而无需将私钥暴露给任何单个参与者。这种钱包具有高度的安全性和隐私性。实现一个 MPC …...

每日算法刷题Day19 5.31:leetcode二分答案3道题,用时1h
6. 475.供暖器(中等,学习check函数双指针思想) 475. 供暖器 - 力扣(LeetCode) 思想 1.冬季已经来临。 你的任务是设计一个有固定加热半径的供暖器向所有房屋供暖。在加热器的加热半径范围内的每个房屋都可以获得供暖。现在,给出…...

【线上故障排查】缓存热点Key导致Redis性能下降的排查与优化
一、高频面试题 什么是缓存热点Key?它会对Redis性能产生哪些影响? 缓存热点Key是指在某段时间内,被大量请求访问的缓存Key。由于Redis是单线程模型,大量针对热点Key的请求会导致该线程长时间处于忙碌状态,其他请求只能排队等待处理,从而使Redis整体响应延迟增加,吞吐量下…...

关于镜像如何装进虚拟机
本篇文章为感谢小仙猪老师特别编写 本篇文章仅以Ubuntu为例 目录 创建虚拟机 汉化 如果没有China选项 检查网络 创建虚拟机 第一步,创建虚拟机 因为,第一个选项是会把虚拟机的文件放在c盘因此,这里博主选择自定义,然后下一…...

CPU特权级别:硬件与软件协同构建系统安全的基石
在计算机系统的底层架构中,用户模式(User Mode)与内核模式(Kernel Mode)的划分是保障系统安全与稳定的核心机制。这一机制的实现既依赖于CPU硬件的特权级别设计,也离不开操作系统的精细化管理。本文将从硬件…...

智慧体育馆数字孪生,场馆管理智能化
图扑数字孪生智慧体育馆可视化管理平台。通过高精度三维建模,对体育馆建筑结构、设施设备等进行 1:1 虚拟映射,全方位还原场馆物理实体。系统集成多维度传感器数据,实现对人流量、客流密度、区域拥堵指数等信息的实时采集与分析,动…...

回归算法模型之线性回归
哈喽!我是 我不是小upper~ 今天来和大家聊聊「线性回归」—— 这是机器学习里最基础、最直观的算法之一,咱们用一个超简单的例子就能搞懂它! 先看一个生活场景 假设你是房产中介,遇到一个灵魂拷问: 客户有…...

【深度学习】10. 深度推理(含链式法则详解)RNN, LSTM, GRU,VQA
深度推理(含链式法则详解)RNN, LSTM, GRU,VQA RNN 输入表示方式 在循环神经网络(Recurrent Neural Network, RNN)中,我们处理的是一段文字或语音等序列数据。对于文本任务,输入通常是单词序列…...

【Java】在 Spring Boot 中连接 MySQL 数据库
在 Spring Boot 中连接 MySQL 数据库是一个常见的任务。Spring Boot 提供了自动配置功能,使得连接 MySQL 数据库变得非常简单。以下是详细的步骤: 一、添加依赖 首先,确保你的pom.xml文件中包含了 Spring Boot 的 Starter Data JPA 和 MySQ…...

影响服务器稳定性的因素都有什么?
服务器的稳定性会影响到业务是否能够持续运行,用户在进行访问网站的过程中是否出现页面卡顿的情况,本文就来了解一下都是哪些因素影响着服务器的稳定性。 服务器中的硬件设备是保证服务器稳定运行的基础,企业选择高性能的处理器和大容量且高速…...

【Qt】Bug:findChildren找不到控件
使用正确的父对象调用 findChildren:不要在布局对象上调用 findChildren,而应该在布局所在的窗口或控件上调用。...
)
GitHub 趋势日报 (2025年05月30日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 833 agenticSeek 789 prompt-eng-interactive-tutorial 466 ai-agents-for-beginn…...

【linux】linux进程概念(四)(环境变量)超详细版
小编个人主页详情<—请点击 小编个人gitee代码仓库<—请点击 linux系列专栏<—请点击 倘若命中无此运,孤身亦可登昆仑,送给屏幕面前的读者朋友们和小编自己! 目录 前言一、基本概念二、认识常见的几个环境变量echo $ 查看某个环境变量env 显示…...

Qt程序添加调试输出窗口:CONFIG += console
目录 1.背景 2.解决方案 3.原理详解 4.控制台窗口的行为 5.条件编译(仅调试模式显示控制台) 6.替代方案 7.总结 1.背景 在Qt程序开发中,开发者经常遇到这样的困扰: 开发机上程序运行正常 发布到其他机器后程序无法启动 …...
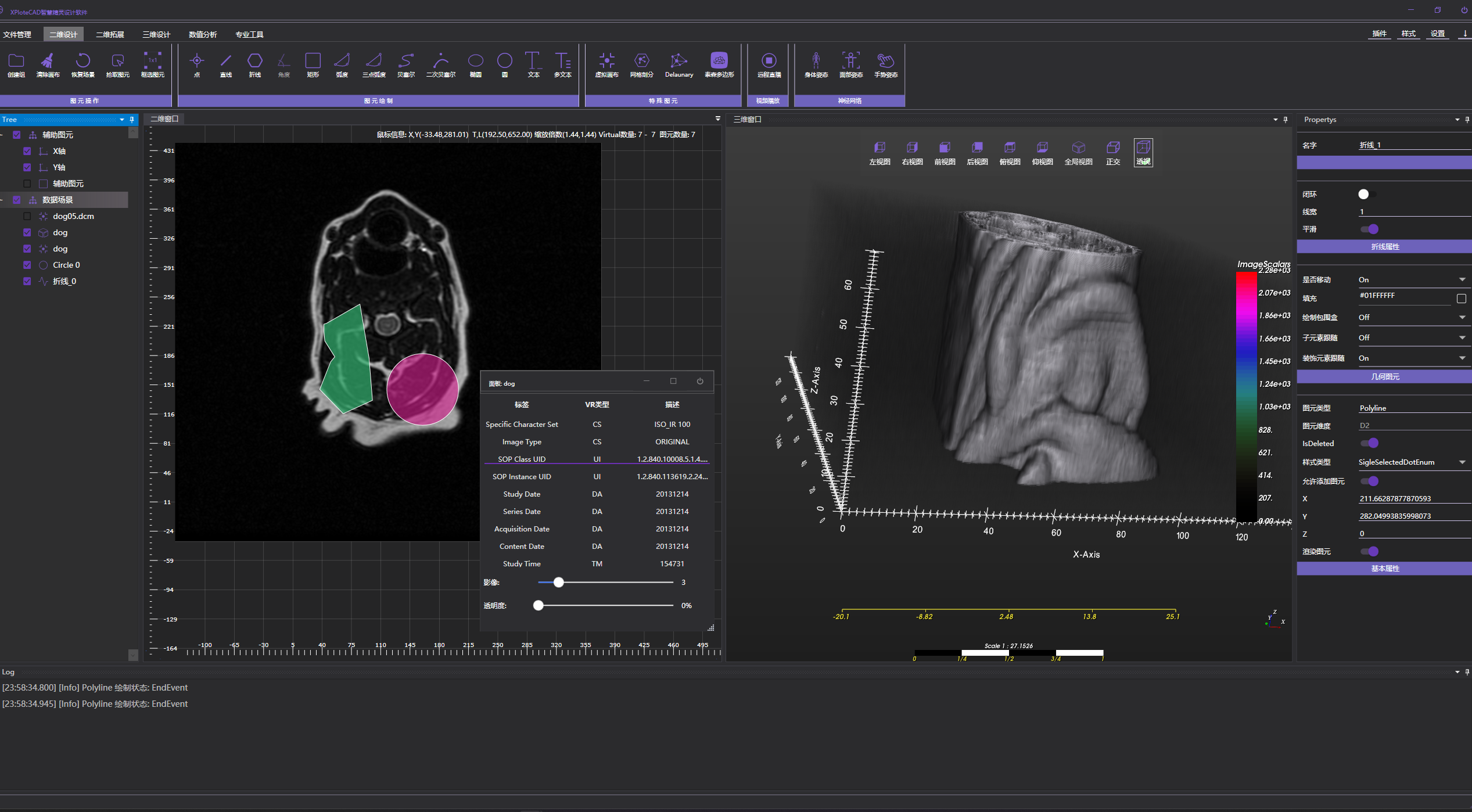
从零开始的二三维CAD|CAE软件: 解决VTK,DICOM体素化-失效问题.
背景: 在从零开始的二三维软件开发中, 需要加载CT的dicoms影像文件, 并将其序列化之后的数据,体素化 可惜..vtk的c#库,将其体素化的时候,竟然失败... 使用vtkDicomReader ,设置 Dicom文件夹读取,竟然不停的失败...从网上找了一些版本.也没啥可用的资料... 解决办法: 直接…...

android协程异步编程常用方法
在 Android 开发中,Kotlin 协程是处理异步操作的首选方案,它能让异步代码更简洁、更易读。以下是 Android 协程异步编程的常用方法和模式: 一、基础构建块 1. launch 作用:启动一个新协程,不返回结果。适用场景&…...

【计算机网络】应用层协议Http——构建Http服务服务器
🔥个人主页🔥:孤寂大仙V 🌈收录专栏🌈:计算机网络 🌹往期回顾🌹: 【Linux笔记】——进程间关系与守护进程 🔖流水不争,争的是滔滔不息 一、Http协…...

【求A类B类月】2022-2-9
缘由编程求解,如内容所示题-Python-CSDN问答只写示例及注释 每月工作日只考虑周末情况,即只有周六、周日放假。每月第一个工作日如果是星期一则该月是A类月,每月最后一个工作日如果是星期五则该月是B类月。一个月可能是A类月也可能是B类月。…...

信息安全之为什么引入公钥密码
在对称密码中,由于加密和解密的密钥是相同的,因此必须向接收者配送密钥,这里就涉及到密钥配送问题 那么什么时候密钥配送问题呢?举个简单的例子大家就清楚了, Alice 前几天在网上认识了Bob,现在她想给Bob…...
