多目标粒子群优化算法(MOPSO),用于解决无人机三维路径规划问题,Matlab代码实现
多目标粒子群优化算法(MOPSO),用于解决无人机三维路径规划问题,Matlab代码实现
目录
- 多目标粒子群优化算法(MOPSO),用于解决无人机三维路径规划问题,Matlab代码实现
- 效果一览
- 基本介绍
- 程序设计
- 参考资料
效果一览





基本介绍
代码功能
该代码实现了一个多目标粒子群优化算法(MOPSO),用于解决三维路径规划问题(如无人机避障路径规划)。核心功能是通过球坐标系表示路径节点,优化路径的多个目标(如路径长度、安全性等),最终输出Pareto最优解并可视化。
算法步骤
问题定义
加载环境模型(包含地图、起点、终点、障碍物)
设置路径节点数(决策变量)和球坐标系边界(距离r、俯仰角ψ、方位角φ)
初始化粒子群
随机生成粒子位置(球坐标)和速度
转换球坐标为笛卡尔坐标并计算多目标代价
初始化个体最优和全局最优解
MOPSO主循环
a. 粒子更新
从存档中选择全局最优(领导者)
分别更新球坐标三个分量(r, ψ, φ)的速度和位置
边界处理:速度镜像反弹 + 位置截断
b. 评估与变异
将新位置转为笛卡尔坐标并计算代价
自适应变异:以概率pm生成新解,根据支配关系决定是否接受
c. 更新最优解
比较当前解与个体历史最优,按支配关系或50%概率更新
d. 存档管理
添加新的非支配解到外部存档
移除被支配解
网格自适应:划分目标空间并分配解到网格
存档溢出时删除拥挤区域解
结果输出
从最终存档中选择最优解
转换为笛卡尔坐标并绘制3D路径
用场景
无人机/机器人路径规划
在三维环境中避开障碍物,生成安全、高效的路径
优化目标示例:路径长度最小化、远离障碍物、能耗最低
多目标优化问题
适用于任何需同时优化多个冲突目标的场景
如:成本vs时间、精度vs效率等权衡问题
三维空间导航
利用球坐标系自然约束方向变化
适合空中/水下载体的平滑路径生成
算法特点
球坐标表示
用(r, ψ, φ)代替(x,y,z),简化方向控制
约束角度变化范围(±π/4)保证路径平滑性
多目标处理
外部存档保存Pareto前沿
自适应网格管理解的分布密度
基于拥挤度删除存档解(gamma=2偏好稀疏区域)
自适应变异
变异概率随迭代下降:pm = (1-迭代比)^(1/mu)
变异步长由delta控制,增强局部搜索能力
边界处理
位置越界时采用速度镜像反弹(物理合理性)
速度边界基于位置范围动态计算(α=0.5)
程序设计
- 完整程序和数据下载私信博主回复多目标粒子群优化算法(MOPSO),用于解决无人机三维路径规划问题,Matlab代码实现。
clc; close; clear all;
%% 问题定义
model = CreateModel(); % 创建模型(包含地图、起点、终点等参数)
model_name = 6; % 模型编号nVar=model.n; % 决策变量数量(路径节点数)
VarSize=[1 nVar]; % 决策变量矩阵大小% 粒子位置边界(球坐标系)
VarMin.x=model.xmin; % x最小值
VarMax.x=model.xmax; % x最大值
VarMin.y=model.ymin; % y最小值
VarMax.y=model.ymax; % y最大值
VarMin.z=model.zmin; % z最小值
VarMax.z=model.zmax; % z最大值 % 球坐标距离r的范围(基于起点-终点距离计算)
VarMax.r=3*norm(model.start-model.end)/nVar;
VarMin.r=VarMax.r/9;% 俯仰角(elevation)范围
AngleRange = pi/4; % 角度变化范围限制
VarMin.psi=-AngleRange; % 最小俯仰角
VarMax.psi=AngleRange; % 最大俯仰角 % 方位角(azimuth)范围
VarMin.phi=-AngleRange; % 最小方位角
VarMax.phi=AngleRange; % 最大方位角 % 速度边界(基于位置范围计算)
alpha=0.5; % 速度范围系数
VelMax.r=alpha*(VarMax.r-VarMin.r); % 距离r的最大速度
VelMin.r=-VelMax.r; % 距离r的最小速度
VelMax.psi=alpha*(VarMax.psi-VarMin.psi); % 俯仰角的最大速度
VelMin.psi=-VelMax.psi; % 俯仰角的最小速度
VelMax.phi=alpha*(VarMax.phi-VarMin.phi); % 方位角的最大速度
VelMin.phi=-VelMax.phi; % 方位角的最小速度 % 代价函数句柄(多目标)
CostFunction=@(x) MyCost(x,model,VarMin); % 输入笛卡尔坐标,输出多目标代价向量%% PSO Parameters
% 获取目标函数数量
dummy_output = CostFunction(struct('x', ones(1, model.n), 'y', ones(1, model.n), 'z', ones(1, model.n)));
nObj = numel(dummy_output); % 目标数量MaxIt = 500; % 最大迭代次数
nPop = 100; % 种群大小
nRep = 50; % 外部存档大小(存储非支配解)% PSO 参数
w = 1; % 惯性权重
wdamp = 0.98; % 惯性权重衰减率
c1 = 1.5; % 个体学习因子
c2 = 1.5; % 全局学习因子参考资料
[1] https://blog.csdn.net/kjm13182345320/article/details/128163536?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/kjm13182345320/article/details/128151206?spm=1001.2014.3001.5502
相关文章:

多目标粒子群优化算法(MOPSO),用于解决无人机三维路径规划问题,Matlab代码实现
多目标粒子群优化算法(MOPSO),用于解决无人机三维路径规划问题,Matlab代码实现 目录 多目标粒子群优化算法(MOPSO),用于解决无人机三维路径规划问题,Matlab代码实现效果一览基本介绍…...

工厂模式 vs 策略模式:设计模式中的 “创建者” 与 “决策者”
在日常工作里,需求变动或者新增功能是再常见不过的事情了。而面对这种情况时,那些耦合度较高的代码就会给我们带来不少麻烦,因为在这样的代码基础上添加新需求往往困难重重。为了保证系统的稳定性,我们在添加新需求时,…...
-Qwen2.5-VL-7B LORA微调OCR数据集)
23、Swift框架微调实战(3)-Qwen2.5-VL-7B LORA微调OCR数据集
一、模型介绍 Qwen2.5-VL 是阿里通义千问团队开源的视觉语言模型,具有3B、7B和72B三种不同规模,能够识别常见物体、分析图像中的文本、图表等元素,并具备作为视觉Agent的能力。 Qwen2.5-VL 具备作为视觉Agent的能力,可以推理并动态使用工具,初步操作电脑和手机。在视频处…...

37. Sudoku Solver
题目描述 37. Sudoku Solver 回溯 class Solution {vector<vector<bool>> row_used;vector<vector<bool>> col_used;vector<vector<bool>> box_used;public:void solveSudoku(vector<vector<char>>& board) {row_used.r…...

C# Renci.SshNet 登陆 suse配置一粒
C# 调用Renci.SshNet 的SSH类库,登陆 suse linux系统,如果没有配置,会报错: Renci.SshNet.Common.SshAuthenticationException: No suitable authentication method found to complete 1、需要root登陆os,配置 /etc/ssh/sshd_con…...

RV1126-OPENCV 图像叠加
一.功能介绍 图像叠加:就是在一张图片上放上自己想要的图片,如LOGO,时间等。有点像之前提到的OSD原理一样。例如:下图一张图片,在左上角增加其他图片。 二.OPENCV中图像叠加常用的API 1. copyTo方法进行图像叠加 原理…...

修改 vscode 左侧导航栏的文字大小 (更新版)
1. 起因, 目的: 问题: vscode 左侧的文字太小了!!!我最火的一篇文章,写的就是这个问题。 看来这个问题,是很广泛的一个痛点。我最近更新了 vscode, 这个问题又出现了。再来搞一下。…...

从C++编程入手设计模式2——工厂模式
从C编程入手设计模式 工厂模式 我们马上就要迎来我们的第二个创建型设计模式:工厂方法模式(Factory Method Pattern)。换而言之,我们希望使用一个这样的接口,使用其他手段而不是直接创建的方式(说的有…...

云原生 Cloud Native Build (CNB)使用初体验
云原生 Cloud Native Build(CNB)使用初体验 引言 当“一切皆可云”成为趋势,传统开发环境正被云原生工具重塑。腾讯云CNB(Cloud Native Build)作为一站式开发平台,试图解决多环境协作难题。 本文将分享c…...

格式工厂 FormatFactory v5.20.便携版 ——多功能媒体文件转换工具 长期更新
—————【下 载 地 址】——————— 【本章下载一】:https://pan.xunlei.com/s/VORWF3Q7D0eCVV06LHbzheD-A1?pwdjikz# 【本章下载二】:https://pan.quark.cn/s/8ee59ed83658 【百款黑科技】:https://ucnygalh6wle.feishu.cn/wiki/…...

数据可视化--使用matplotlib绘制高级图表
目录 一、绘制等高线图 contour() 二、绘制矢量场流线图 streamplot() 三、绘制棉棒图 stem() 四、绘制哑铃图 五、绘制甘特图 六、绘制人口金字塔图 barh() 七、绘制漏斗图 简易版漏斗图 八、绘制桑基图 Sankey()---创建桑基图 add()---添加桑基图的选项 finish()…...
完全指南:从原理到实战)
卷积神经网络(CNN)完全指南:从原理到实战
卷积神经网络(CNN)完全指南:从原理到实战 引言:为什么CNN改变了计算机视觉? 2012年,AlexNet在ImageNet竞赛中以压倒性优势获胜,将错误率降低了近10个百分点,这标志着卷积神经网络(CNN)时代的开始。如今&a…...

如何做好一个决策:基于 Excel的决策树+敏感性分析应用
决策点: 开发新产品? (是 / 否) 因素 (如果是): 市场接受度 (高 / 中 / 低);概率: 高(0.3), 中(0.5), 低(0.2) 结果值 (NPV): 高(+$1M), 中(+$0.2M), 低(-$0.5M) 不开发成本/收益: $0 开发计算: EMV(市场接受度) = (0.3 * 1M) + (0.5 * 0.2M) + (0.2 * -0.5M) = $0.3M + $…...

【模拟电子电路-工具使用】
模拟电子电路-工具使用 ■ 1. 模拟软件■ 1. circuit JS ■ 2. 万用表■ 3. 示波器■ 4.■ 5.■ 6.■ 7. ■ 1. 模拟软件 ■ 1. circuit JS ■ 2. 万用表 ■ 3. 示波器 ■ 4. ■ 5. ■ 6. ■ 7....

[ElasticSearch] ElasticSearch的初识与基本操作
🌸个人主页:https://blog.csdn.net/2301_80050796?spm1000.2115.3001.5343 🏵️热门专栏: 🧊 Java基本语法(97平均质量分)https://blog.csdn.net/2301_80050796/category_12615970.html?spm1001.2014.3001.5482 🍕 Collection与…...
)
Spring AI 代理模式(Agent Agentic Patterns)
一、Agentic Patterns 核心思想 根据Anthropic《构建高效代理》研究报告,高效LLM代理的设计应遵循两大核心原则: 简单性优先:避免过度设计,从最简单的解决方案开始可组合性:通过模块化设计实现灵活组合而非复杂框架 …...
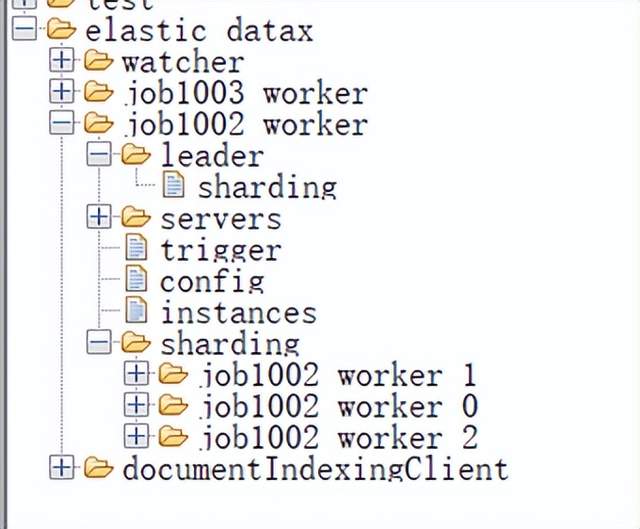
搜索引擎2.0(based elasticsearch6.8)设计与实现细节(完整版)
1 简介 1.1 背景 《搜索引擎onesearch 1.0-设计与实现.docx》介绍了1.0特性,搜索schema,agg,表达式搜索映射,本文介绍onesearch 2.0 新特性, 参考第2节 规划特性与发布计划 1.2 关键词 文档 Document elasticsearch 一行数据称为…...

ps中前景色和背景色
在Photoshop(简称PS)中,前景色和背景色是两个非常重要的概念,它们直接影响着绘图、填充、渐变等操作的最终效果。以下是对前景色和背景色的全面、深入解释: 一、前景色与背景色的定义 前景色:指的是当前绘…...
)
网页前端开发(基础进阶2--JS)
前面学习了html与css,接下来学习JS(JavaScript与Java无关)。 web标准(网页标准)分为3个部分: 1.html主要负责网页的结构(页面的元素和内容) 2.css主要负责网页的表现(…...

Go 即时通讯系统:客户端与服务端 WebSocket 通信交互
客户端和服务端的交互 客户端与服务端建立连接 客户端:客户端通过浏览器或者其他应用程序发起一个 HTTP 请求到服务端的 /socket.io 路径。在请求中会携带用户的 UUID 作为参数(通过 c.Query("user") 获取)。 // router/socket.…...
:大模型多模态突破 具身智能开启机器人新纪元)
2025年5月AI科技领域周报(5.19-5.25):大模型多模态突破 具身智能开启机器人新纪元
2025年5月AI科技领域周报(5.19-5.25):大模型多模态突破 具身智能开启机器人新纪元 目录 2025年5月AI科技领域周报(5.19-5.25):大模型多模态突破 具身智能开启机器人新纪元一、本周热点回顾1. 百度发布全球首…...

某航后缀混淆逆向与顶像风控分析
文章目录 1. 写在前面2. 接口分析3. 加密分析4. 风控分析 【🏠作者主页】:吴秋霖 【💼作者介绍】:擅长爬虫与JS加密逆向分析!Python领域优质创作者、CSDN博客专家、阿里云博客专家、华为云享专家。一路走来长期坚守并致…...

[Protobuf]常见数据类型以及使用注意事项
[Protobuf]常见数据类型以及使用注意事项 水墨不写bug 文章目录 一、基本数据类型1、字段2、字段的修饰规则 二、自定义数据类型1、message类型2、enum类型3、Any类型4、oneof类型5、map类型 三、小工具1.hexdump2.decode 四、注意事项 一、基本数据类型 protobuf 支持多种基础…...

【C/C++】面试基础题目收集
C 软件开发面试中常见的刷题题目通常可分为以下几大类:数据结构与算法、系统编程、面向对象设计、C 语言特性、并发编程等。 🧠 一、数据结构与算法(力扣/牛客经典题) 掌握 STL 和底层结构实现能力: 📌 数…...

模拟实现线程池(线程数目为定值)和定时器
前言 昨天学习关于定时器的相关知识。今天花时间去模拟实现了一个定时器,同时也去模拟实现了一个线程池(线程数目为定值)。我感觉我收获了很多,对于线程的理解加深了。跟大家分享一下~ 线程池和定时器(这个是主要)的实现 代码 线程池 import java.ut…...

数据结构之队列实验
引言 在计算机科学中,进制转换是基础但重要的操作。例如将一个十进制数转换为二进制或八进制表示时,我们通常使用“短除法”——即不断用目标进制去除当前数,记录余数,直到商为0为止。 这种方法得到的是低位先产生的结果&#x…...

Java求职者面试题详解:计算机网络、操作系统、设计模式与数据结构
Java求职者面试题详解:计算机网络、操作系统、设计模式与数据结构 第一轮:基础概念问题 1. 请解释什么是HTTP协议? HTTP(HyperText Transfer Protocol)是一种用于传输超文本的协议,它定义了客户端和服务…...

每日八股文6.1
每日八股-6.1 Go1.Sync.map的底层实现2.结构体的tag如何获取?3.Go实现单例模式(使用sync.Once)4.Go实现单例模式(不使用sync.Once)5.make和new的区别6.Go项目引用包为什么用_以及包的init()函数7.如何判断一个结构体是…...

【Ubuntu】摸鱼技巧之虚拟机环境复制
前言 提示:所有的操作都需要关闭虚拟机 如何快速在其它电脑布置,linux环境,如果我们有一个环境直接拷贝就有时间摸鱼呀。 1.直接复制简单粗暴 不做赘述,如果不会复制,那么请右击鼠标压缩复制 2.克隆虚拟机 2.1 …...

室内VR全景助力房产营销及装修
在当今的地产行业,VR全景已成为不可或缺的应用工具。从地产直播到楼市VR地图,从效果图到水电家装施工记录,整个地产行业的上下游生态中,云VR全景的身影无处不在。本文将探讨VR全景在房产营销及装修领域的应用,并介绍众…...
