【笔记】MLA矩阵吸收分析
文章目录
- 一、张量运算的计算量
- 1. FLOPs定义
- 2. 张量计算顺序对计算量的影响
- 二、MLA第一次矩阵吸收的计算量分析
- 1. 原始注意力计算
- 2. MLA源代码中的吸收方式
- 3. 提前吸收
- 4. 比较分析
- 4.1 比较顺序1和顺序2
- 4.2 比较顺序2和顺序3
- 三、MLA第二次矩阵吸收的计算量分析
- 1. 原始输出计算
- 2. MLA源代码中的吸收方式
- 3. 提前吸收
- 4. 比较分析
- 4.1 比较顺序1和顺序2
- 4.2 比较顺序2和顺序3
- 参考链接
一、张量运算的计算量
1. FLOPs定义
FLOPs:Floating Point Operations 指的是浮点运算次数,一般特指乘加运算次数,理解为计算量,可以用来衡量算法/模型时间的复杂度。更大的计算量单位通常包括:
- MFLOPs:百万次浮点运算( 10 6 10^6 106 FLOPs)。
- GFLOPs:十亿次浮点运算( 10 9 10^9 109 FLOPs)。
- TFLOPs:万亿次浮点运算( 10 12 10^{12} 1012 FLOPs)。
张量运算的计算量通常与运算维度和操作类型有关,以pytorch中线性层nn.Linear的计算为例,设输入张量的维度为 B × S × D B \times S \times D B×S×D,线性层内部权重矩阵维度为 D × O D \times O D×O:
- 若不考虑
bias,两个张量相乘的结果维度为 B × S × O B \times S \times O B×S×O,结果中的每个元素是由原始张量分别沿着 D D D维度进行了 D D D次乘法和 D − 1 D-1 D−1次加法而来的,因此总计算量为:
( 2 D − 1 ) × B × S × O (2D-1)\times B \times S \times O (2D−1)×B×S×O
- 若考虑
bias,则每个元素由原始张量分别沿着 D D D维度进行 D D D次乘法和 D − 1 D-1 D−1次加法后,还需加上bias,因此一共也执行了 D D D次加法,总计算量为:
2 D × B × S × O 2D \times B \times S \times O 2D×B×S×O
为了简单起见,后续分析时均以考虑bias来分析,这样FLOPs的计算可直接由相关维度的相乘而来。
2. 张量计算顺序对计算量的影响
张量计算顺序的不同会影响计算量。以下是一个例子:
假设有三个张量 A A A、 B B B 和 C C C,它们的形状分别为:
- A A A: ( m , n ) (m, n) (m,n)
- B B B: ( n , p ) (n, p) (n,p)
- C C C: ( p , q ) (p, q) (p,q)
我们需要计算 A × B × C A \times B \times C A×B×C,其中 × \times × 表示矩阵乘法。
计算顺序 1:先计算 A × B A \times B A×B,再乘以 C C C
- 计算 A × B A \times B A×B:
- 结果形状为 ( m , p ) (m, p) (m,p)。
- 每个元素的计算量为 2 n 2n 2n( n n n 次乘法和 n n n 次加法)。
- 总计算量: m × p × 2 n = 2 m n p m \times p \times 2n = 2mnp m×p×2n=2mnp。
- 计算 ( A × B ) × C (A \times B) \times C (A×B)×C:
- 结果形状为 ( m , q ) (m, q) (m,q)。
- 每个元素的计算量为 2 p 2p 2p( p p p 次乘法和 p p p 次加法)。
- 总计算量: m × q × 2 p = 2 m p q m \times q \times 2p = 2mpq m×q×2p=2mpq。
- 总计算量: 2 m n p + 2 m p q 2mnp + 2mpq 2mnp+2mpq。
计算顺序 2:先计算 B × C B \times C B×C,再乘以 A A A
- 计算 B × C B \times C B×C:
- 结果形状为 ( n , q ) (n, q) (n,q)。
- 每个元素的计算量为 2 p 2p 2p( p p p 次乘法和 p p p 次加法)。
- 总计算量: n × q × 2 p = 2 n p q n \times q \times 2p = 2npq n×q×2p=2npq。
- 计算 A × ( B × C ) A \times (B \times C) A×(B×C):
- 结果形状为 ( m , q ) (m, q) (m,q)。
- 每个元素的计算量为 2 n 2n 2n( n n n 次乘法和 n n n 次加法)。
- 总计算量: m × q × 2 n = 2 m n q m \times q \times 2n = 2mnq m×q×2n=2mnq。
- 总计算量: 2 n p q + 2 m n q 2npq + 2mnq 2npq+2mnq。
比较两种计算顺序:
-
计算顺序 1的总计算量为 2 m n p + 2 m p q 2mnp + 2mpq 2mnp+2mpq。
-
计算顺序 2的总计算量为 2 n p q + 2 m n q 2npq + 2mnq 2npq+2mnq。
-
将上述两式相减,有:
2 [ m n ( p − q ) + p q ( m − n ) ] 2[mn(p-q)+pq(m-n)] 2[mn(p−q)+pq(m−n)]
可见如果 p < q , m < n p<q,m<n p<q,m<n则必定计算顺序1的计算量更小,如果 p > q , m > n p>q,m>n p>q,m>n则反之,其余情况 则需根据具体数值分析。
二、MLA第一次矩阵吸收的计算量分析
我们比较三种计算顺序:
假设原始序列 h \mathbf{h} h经Q低秩压缩后得到 c Q \mathbf{c}^Q cQ,经KV低秩压缩得到 c K V \mathbf{c}^{KV} cKV,它们的上投影矩阵分别为 W U Q W^{UQ} WUQ和 W U K W^{UK} WUK。
1. 原始注意力计算
原始注意力计算如下:
( W U Q c Q ) T ( W U K c K V ) (W^{UQ}\mathbf{c}^Q)^T (W^{UK}\mathbf{c}^{KV}) (WUQcQ)T(WUKcKV)
上述张量的形状如下,箭头右边是简记的符号,并将n_heads × qk_nope_head_dim进行了拆分:
- W U Q W^{UQ} WUQ :
(q_lora_rank, n_heads × qk_nope_head_dim) -> (q, h, d) - c Q \mathbf{c}^Q cQ :
(bsz, q_seq_len, q_lora_rank) -> (b, s, q) - W U K W^{UK} WUK :
(kv_lora_rank, n_heads × qk_nope_head_dim) -> (k, h, d) - c K V \mathbf{c}^{KV} cKV :
(bsz, k_seq_len, kv_lora_rank) -> (b, t, k) - Step 1: W U Q c Q W^{UQ}\mathbf{c}^Q WUQcQ:
(bsz, q_seq_len, n_heads, qk_nope_head_dim) -> (b, s, h, d) - Step 2: W U K c K V W^{UK}\mathbf{c}^{KV} WUKcKV:
(bsz, k_seq_len, n_heads, qk_nope_head_dim) -> (b, t, h, d) - Step 3: ( W U Q c Q ) T ( W U K c K V ) (W^{UQ}\mathbf{c}^Q)^T (W^{UK}\mathbf{c}^{KV}) (WUQcQ)T(WUKcKV):
(bsz, n_heads, q_seq_len, k_seq_len) -> (b, h, s, t)
这里区分q_seq_len和k_seq_len,训练或prefill时二者是一致的,decode时q_seq_len是1,k_seq_len是cache的长度。
根据张量计算量分析的规则,计算量如下:
FLOPs order 1 = 2 b s h d q + 2 b t h d k + 2 b h s t d \text{FLOPs}_{\text{order}_1}=2bshdq+2bthdk+2bhstd FLOPsorder1=2bshdq+2bthdk+2bhstd
2. MLA源代码中的吸收方式
[ ( W U Q c Q ) T W U K ] c K V [(W^{UQ}\mathbf{c}^Q)^T W^{UK}]\mathbf{c}^{KV} [(WUQcQ)TWUK]cKV
- Step 1: W U Q c Q W^{UQ}\mathbf{c}^Q WUQcQ:
(bsz, q_seq_len, n_heads, qk_nope_head_dim) -> (b, s, h, d) - Step 2: ( W U Q c Q ) T W U K (W^{UQ}\mathbf{c}^Q)^TW^{UK} (WUQcQ)TWUK:
(bsz, q_seq_len, n_heads, kv_lora_rank) -> (b, s, h, k) - Step 3: [ ( W U Q c Q ) T W U K ] c K V [(W^{UQ}\mathbf{c}^Q)^T W^{UK}]\mathbf{c}^{KV} [(WUQcQ)TWUK]cKV:
(bsz, n_heads, q_seq_len, k_seq_len) -> (b, h, s, t)
计算量如下:
FLOPs order 2 = 2 b s h d q + 2 b s h k d + 2 b h s t k \text{FLOPs}_{\text{order}_2}=2bshdq+2bshkd+2bhstk FLOPsorder2=2bshdq+2bshkd+2bhstk
3. 提前吸收
c Q T ( W U Q T W U K ) c K V {\mathbf{c}^Q}^T(W^{UQ^T} W^{UK})\mathbf{c}^{KV} cQT(WUQTWUK)cKV
- Step 1: W U Q T W U K W^{UQ^T} W^{UK} WUQTWUK:
(n_heads, q_lora_rank, kv_lora_rank) -> (h, q, k) - Step 2: c Q T ( W U Q T W U K ) {\mathbf{c}^Q}^T(W^{UQ^T} W^{UK}) cQT(WUQTWUK):
(bsz, q_seq_len, n_heads, kv_lora_rank) -> (b, s, h, k) - Step 3: c Q T ( W U Q T W U K ) c K V {\mathbf{c}^Q}^T(W^{UQ^T} W^{UK})\mathbf{c}^{KV} cQT(WUQTWUK)cKV:
(bsz, n_heads, q_seq_len, k_seq_len) -> (b, h, s, t)
计算量如下:
FLOPs order 3 = 2 h q k d + 2 b s h k q + 2 b h s t k \text{FLOPs}_{\text{order}_3}=2hqkd+2bshkq+2bhstk FLOPsorder3=2hqkd+2bshkq+2bhstk
4. 比较分析
4.1 比较顺序1和顺序2
首先比较 FLOPs order 1 \text{FLOPs}_{\text{order}_1} FLOPsorder1和 FLOPs order 2 \text{FLOPs}_{\text{order}_2} FLOPsorder2,有:
FLOPs order 1 − FLOPs order 2 = 2 b h d k ( t − s ) + 2 b h s t ( d − k ) \text{FLOPs}_{\text{order}_1}-\text{FLOPs}_{\text{order}_2}= 2bhdk(t-s)+2bhst(d-k) FLOPsorder1−FLOPsorder2=2bhdk(t−s)+2bhst(d−k)
其中:
t:k_seq_lens:q_seq_lend:qk_nope_head_dim = 128k:kv_lora_rank = 512h:n_heads = 128b:bsz由于第一项和第二项都有b,为简单起见,设为1
在训练或prefill阶段,t=s,上式结果为 − 98304 s 2 -98304s^2 −98304s2,此时顺序1的计算量更优。
在decode阶段,t是缓存长度,而s=1,上式结果为 16777216 ( t − 1 ) − 98304 t = 16678912 t − 16777216 16777216(t-1)-98304t=16678912t-16777216 16777216(t−1)−98304t=16678912t−16777216,可见,推理时随着缓存长度t的变大,顺序1需要花费更大的计算量,因此才需要把 W U K W^{UK} WUK吸收进 W U Q c Q W^{UQ}\mathbf{c}^Q WUQcQ(也就是代码中的q_nope)中,避免产生的中间量需要大量的计算。
4.2 比较顺序2和顺序3
然后比较 FLOPs order 2 \text{FLOPs}_{\text{order}_2} FLOPsorder2和 FLOPs order 3 \text{FLOPs}_{\text{order}_3} FLOPsorder3,有:
FLOPs order 2 − FLOPs order 3 = 2 h d q ( b s − k ) + 2 b s h k ( d − q ) \text{FLOPs}_{\text{order}_2}-\text{FLOPs}_{\text{order}_3}= 2hdq(bs-k)+2bshk(d-q) FLOPsorder2−FLOPsorder3=2hdq(bs−k)+2bshk(d−q)
其中:
q:q_lora_rank = 1536b:bsz第一项的b无法作为因子提出,因此先不假定具体值
上式结果中不包含t,结果为 50331648 ( b s − 512 ) − 184549376 b s = − 134217728 b s − 25769803776 50331648(bs-512)-184549376bs=-134217728bs-25769803776 50331648(bs−512)−184549376bs=−134217728bs−25769803776,恒小于0,因此顺序2的计算量优于顺序3。其原因是 ( W U Q T W U K ) (W^{UQ^T} W^{UK}) (WUQTWUK)充当了新的 W U Q ′ W^{UQ'} WUQ′,其形状为(h, q, k),具有100663296个元素。而 W U Q W^{UQ} WUQ和 W U K W^{UK} WUK的形状分别为(q, h, d)和(k, h, d),二者之和只有33554432个元素,约为 W U Q ′ W^{UQ'} WUQ′的33%,这就解释了虽然公式上直接将 W U K W^{UK} WUK吸收进了 W U Q W^{UQ} WUQ,但为什么代码实现上不这么做的原因。不论是从参数量占用还是计算量上,顺序3都没有优势。
三、MLA第二次矩阵吸收的计算量分析
同样比较三种计算顺序:
假设得到的score形状大小为(bsz, n_heads, q_seq_len, k_seq_len), c K V \mathbf{c}^{KV} cKV向value的上投影矩阵为 W U V W^{UV} WUV,输出维度变换 矩阵为 W O W^O WO。
1. 原始输出计算
原始计算顺序如下:
W O [ s c o r e ( W U V c K V ) ] W^O[score(W^{UV} \mathbf{c}^{KV})] WO[score(WUVcKV)]
上述张量的形状如下,将n_heads × v_head_dim进行了拆分:
- s c o r e score score:
(bsz, n_heads, q_seq_len, k_seq_len) -> (b, h, s, t) - c K V \mathbf{c}^{KV} cKV:
(bsz, k_seq_len, kv_lora_rank) -> (b, t, k) - W U V W^{UV} WUV:
(kv_lora_rank, n_heads × v_head_dim) -> (k, h, v) - W O W^O WO:
(n_heads × v_head_dim, dim) -> (h, v, e) - Step 1: W U V c K V W^{UV} \mathbf{c}^{KV} WUVcKV:
(bsz, k_seq_len, n_heads, v_head_dim) -> (b, t, h, v) - Step 2: [ s c o r e ( W U V c K V ) ] [score(W^{UV} \mathbf{c}^{KV})] [score(WUVcKV)]:
(bsz, n_heads, q_seq_len, v_head_dim) -> (b, h, s, v) - Step 3: W O [ s c o r e ( W U V c K V ) ] W^O[score(W^{UV} \mathbf{c}^{KV})] WO[score(WUVcKV)]:
(bsz, n_heads, q_seq_len, dim) -> (b, h, s, e)
计算量如下:
FLOPs order 1 = 2 b t h v k + 2 b h s v t + 2 b h s e v \text{FLOPs}_{\text{order}_1}=2bthvk+2bhsvt+2bhsev FLOPsorder1=2bthvk+2bhsvt+2bhsev
2. MLA源代码中的吸收方式
W O [ W U V ( s c o r e c K V ) ] W^O[W^{UV} (score\mathbf{c}^{KV})] WO[WUV(scorecKV)]
- Step 1: s c o r e c K V score\mathbf{c}^{KV} scorecKV:
(bsz, n_heads, q_seq_len, kv_lora_rank) -> (b, h, s, k) - Step 2: [ W U V ( s c o r e c K V ) ] [W^{UV} (score\mathbf{c}^{KV})] [WUV(scorecKV)]:
(bsz, n_heads, q_seq_len, v_head_dim) -> (b, h, s, v) - Step 3: W O [ W U V ( s c o r e c K V ) ] W^O[W^{UV} (score\mathbf{c}^{KV})] WO[WUV(scorecKV)]:
(bsz, n_heads, q_seq_len, dim) -> (b, h, s, e)
计算量如下:
FLOPs order 2 = 2 b h s k t + 2 b h s v k + 2 b h s e v \text{FLOPs}_{\text{order}_2}=2bhskt+2bhsvk+2bhsev FLOPsorder2=2bhskt+2bhsvk+2bhsev
3. 提前吸收
( W O W U V ) ( s c o r e c K V ) (W^OW^{UV})(score\mathbf{c}^{KV}) (WOWUV)(scorecKV)
- Step 1: W O W U V W^OW^{UV} WOWUV:
(n_heads, kv_lora_rank, dim) -> (h, k, e) - Step 2: s c o r e c K V score\mathbf{c}^{KV} scorecKV:
(bsz, n_heads, q_seq_len, kv_lora_rank) -> (b, h, s, k) - Step 3: ( W O W U V ) ( s c o r e c K V ) (W^OW^{UV})(score\mathbf{c}^{KV}) (WOWUV)(scorecKV):
(bsz, n_heads, q_seq_len, dim) -> (b, h, s, e)
计算量如下:
FLOPs order 3 = 2 h k e v + 2 b h s k t + 2 b h s e k \text{FLOPs}_{\text{order}_3}=2hkev+2bhskt+2bhsek FLOPsorder3=2hkev+2bhskt+2bhsek
4. 比较分析
4.1 比较顺序1和顺序2
首先比较 FLOPs order 1 \text{FLOPs}_{\text{order}_1} FLOPsorder1和 FLOPs order 2 \text{FLOPs}_{\text{order}_2} FLOPsorder2,有:
FLOPs order 1 − FLOPs order 2 = 2 b h v k ( t − s ) + 2 b h s t ( v − k ) \text{FLOPs}_{\text{order}_1}-\text{FLOPs}_{\text{order}_2}=2bhvk(t-s)+2bhst(v-k) FLOPsorder1−FLOPsorder2=2bhvk(t−s)+2bhst(v−k)
其中:
t:k_seq_lens:q_seq_lenv:v_head_dim = 128k:kv_lora_rank = 512h:n_heads = 128b:bsz由于第一项和第二项都有b,为简单起见,设为1
由于v与d值大小一样,因此计算结果与与第一次矩阵吸收一致。即在训练或prefill阶段,顺序1更优,在decode阶段,顺序2更优。
4.2 比较顺序2和顺序3
然后比较 FLOPs order 2 \text{FLOPs}_{\text{order}_2} FLOPsorder2和 FLOPs order 3 \text{FLOPs}_{\text{order}_3} FLOPsorder3,有:
FLOPs order 2 − FLOPs order 3 = 2 h v k ( b s − e ) + 2 b h s e ( v − k ) \text{FLOPs}_{\text{order}_2}-\text{FLOPs}_{\text{order}_3}=2hvk(bs-e)+2bhse(v-k) FLOPsorder2−FLOPsorder3=2hvk(bs−e)+2bhse(v−k)
其中:
e:dim = 7168b:bsz第一项的b无法作为因子提出,因此先不假定具体值
上式结果为 16777216 ( b s − 7168 ) − 704643072 b s = − 687865856 b s − 120259084288 16777216(bs-7168)-704643072bs=-687865856bs −120259084288 16777216(bs−7168)−704643072bs=−687865856bs−120259084288,可见仍然是顺序2的计算结果更优。
参考链接
- 训练模型算力的单位:FLOPs、FLOPS、Macs 与 估算模型(FC, CNN, LSTM, Transformers&&LLM)的FLOPs - 知乎
- llm 参数量-计算量-显存占用分析 - Zhang
- DeepSeek-V3 MLA 优化全攻略:从低秩压缩到权重吸收,揭秘高性能推理的优化之道 - 知乎
相关文章:

【笔记】MLA矩阵吸收分析
文章目录 一、张量运算的计算量1. FLOPs定义2. 张量计算顺序对计算量的影响 二、MLA第一次矩阵吸收的计算量分析1. 原始注意力计算2. MLA源代码中的吸收方式3. 提前吸收4. 比较分析4.1 比较顺序1和顺序24.2 比较顺序2和顺序3 三、MLA第二次矩阵吸收的计算量分析1. 原始输出计算…...

600+纯CSS加载动画一键获取指南
CSS-Loaders.com 完整使用指南:600纯CSS加载动画库 🎯 什么是 CSS-Loaders.com? CSS-Loaders.com 是一个专门提供纯CSS加载动画的资源网站,拥有超过600个精美的单元素加载器。这个网站的最大特色是所有动画都只需要一个HTML元素…...

开源的JT1078转GB28181服务器
JT1078转GB28181流程 项目地址: JT1078转GB28181的流媒体服务器: https://github.com/lkmio/lkm JT1078转GB28181的信令服务器: https://github.com/lkmio/gb-cms 1. 创建GB28181 UA 调用接口: http://localhost:9000/api/v1/jt/device/add 请求体如下…...

智能守护电网安全:探秘输电线路测温装置的科技力量
在现代电力网络的庞大版图中,输电线路如同一条条 “电力血管”,日夜不息地输送着能量。然而,随着电网负荷不断增加,长期暴露在户外的线路,其线夹与导线在电流热效应影响下,极易出现温度异常。每年因线路过热…...

Java垃圾回收算法及GC触发条件
一、引言 在Java编程语言的发展历程中,内存管理一直是其核心特性之一。与C/C等需要手动管理内存的语言不同,Java通过自动垃圾回收(Garbage Collection,简称GC)机制,极大地减轻了开发人员的负担,…...

【Hot 100】118. 杨辉三角
目录 引言杨辉三角我的解题代码优化优化说明 🙋♂️ 作者:海码007📜 专栏:算法专栏💥 标题:【Hot 100】118. 杨辉三角❣️ 寄语:书到用时方恨少,事非经过不知难! 引言 …...

useMemo useCallback 自定义hook
useMemo & useCallback & 自定义hook useMemo 仅当依赖项发生变化的时候,才去重新计算;其他状态变化时则不去做不必要的计算。 useCallback 缓存函数。但是使用注意📢 ,useCallback没有特别明显的优化。 *合适的场景——父…...
ffmpeg 的视频格式转换 c# win10
1,下载ffmpeg ,并设置环境变量。 ffmpeghttps://www.gyan.dev/ffmpeg/builds/ 2.新建.net 9.0 winform using System; using System.Diagnostics; using System.Text; using System.Windows.Forms;namespace WinFormsApp11 {public partial class Fo…...

【irregular swap】An Examination of Fairness of AI Models for Deepfake Detection
文章目录 An Examination of Fairness of AI Models for Deepfake Detection背景points贡献深伪检测深伪检测审计评估检测器主要发现评估方法审计结果训练分布和方法偏差An Examination of Fairness of AI Models for Deepfake Detection 会议/期刊:IJCAI 2021 作者: 背景…...

【JAVA】注解+元注解+自定义注解(万字详解)
📚博客主页:代码探秘者 ✨专栏:《JavaSe》 其他更新ing… ❤️感谢大家点赞👍🏻收藏⭐评论✍🏻,您的三连就是我持续更新的动力❤️ 🙏作者水平有限,欢迎各位大佬指点&…...

【Doris基础】Apache Doris中的Version概念解析:深入理解数据版本管理机制
目录 引言 1 Version概念基础 1.1 什么是Version 1.2 Version的核心作用 1.3 Version相关核心概念 2 Version工作机制详解 2.1 Version在数据写入流程中的作用 2.2 Version在数据查询流程中的作用 2.3 Version的存储结构 3 Version的进阶特性 3.1 Version的合并与压…...

【Linux 基础知识系列】第一篇-Linux 简介与历史
一、什么是 Linux? Linux 是一种类 Unix 操作系统,它是由 Linus Torvalds 于 1991 年首次发布的。作为一个开源操作系统,Linux 的源代码可以被任何人自由使用、修改和分发。在现代计算环境中,Linux 凭借其强大的性能、高稳定性、…...

【图像处理基石】如何进行图像畸变校正?
图像畸变校正常用于计算机视觉、摄影测量学和机器人导航等领域,能够修正因镜头光学特性或传感器排列问题导致的图像失真。下面我将介绍几种常用的图像畸变校正算法,并提供Python实现和测试用例。 常用算法及Python实现 1. 径向畸变校正 径向畸变是最常…...

软件开发项目管理工具选型及禅道开源版安装
软件开发项目管理工具选型及禅道开源版安装 为啥选禅道 你以为我选禅道之前没有对比吗? 作为Java码农,首先想到的就是Jira,然而它太重了。。 我们用企微作为沟通工具,腾讯的TAPD的确好用,但是它不开源啊,…...

【架构艺术】平衡技术架构设计和预期的产品形态
近期笔者因为工作原因,开始启动team内部部分技术项目的重构。在事情启动的过程中,内部对于这件事情的定性和投入有一些争论,但最终还是敲定了下来。其中部分争论点主要在于产品形态,因为事情涉及到跨部门合作,所以产品…...

电力系统时间同步系统
电力系统中,电压、电流、功率变化等特征量测量都是时间相关函数[1],统一精准的时间源对于电网安全稳定运行至关重要,因此,电力系统运行规程[2]中明确要求继电保护装置、自动化装置、安全稳定控制系统、能量管理系统和生产信息管理…...

Vue使用toFixed保留两位小数的三种写法
第一种:直接写在js里面,这是最简单的 val.toFixed(2)第二种:在ElementUi表格中使用 第三种:在取值符号中使用 {{}} 定义一个方法 towNumber(val) { return val.toFixed(2) } 使用 {{ towNumber(row.equiV…...

华为云【Astro zero】如何做“设备编辑”页面
目录 一、整体原理概述(逻辑图+原理) 1. 页面组件组装(用户交互界面) 2. 数据模型(数据临时存储) 3. 页面事件(逻辑交互) 二、详细操作步骤(按功能模块分) ✅【1】页面创建与结构组装 ✅【2】定义自定义模型与字段(临时数据绑定) ✅【3】定义服务模型(与后…...

Arch安装botw-save-state
devkitPro https://blog.csdn.net/qq_39942341/article/details/148387077?spm1001.2014.3001.5501 cargo https://blog.csdn.net/qq_39942341/article/details/148387783?spm1001.2014.3001.5501 megaton https://blog.csdn.net/qq_39942341/article/details/148388164?spm…...
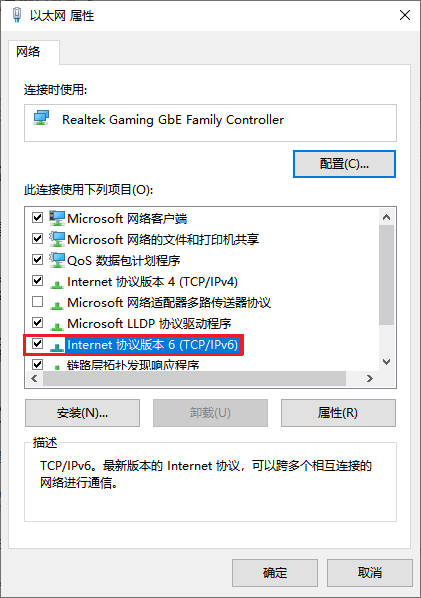
电脑为什么换个ip就上不了网了
在日常使用电脑上网时,很多人可能遇到过这样的问题:当IP地址发生变化后,突然就无法连接网络了。当电脑更换IP地址后无法上网,这一现象可能由多种因素导致,涉及网络配置、硬件限制或运营商策略等层面。以下是系统性分析…...

NULL与空字符串的区别:数据库专家详解
NULL与空字符串的区别:数据库专家详解 1. NULL的概念解析 1.1 NULL的定义 在数据库系统中,NULL是一个特殊标记,表示"未知"或"不存在"的值。它不是任何数据类型的实例,而是表示缺失值的标记。 go专栏&#…...

github 2FA双重认证丢失解决
文章目录 前言一. 凭借ssh 解锁步骤1.1 要求输入设备码1.2.进入二重验证界面1.3.开始2FA恢复1.4.选择使用ssh验证 二.预防措施2.1 云盘上传git_recover_codes.txt2.2 开启多源FA认证2.2.1 大陆无法使用手机验证码 三.参考资料 前言 场景:没有意识到github recovery …...

linux驱动 - 5: simple usb device驱动
参考第2节, 准备好编译环境并实现hello.ko: linux驱动 - 2: helloworld.ko_linux 驱动开发 hello world ko-CSDN博客 下面在hello模块的基础上, 添加代码, 实现一个usb设备驱动的最小骨架. #include <linux/init.h> #include <linux/module.h> #include <lin…...
函数histEven())
OpenCV CUDA模块直方图计算------在 GPU 上计算输入图像的直方图(histogram)函数histEven()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 该函数用于在 GPU 上计算输入图像的直方图(histogram)。它将像素值区间均匀划分为若干个 bin(桶)…...

QT/c++航空返修数据智能分析系统
简介 1、区分普通用户和管理员 2、界面精美 3、功能丰富 4、使用cppjieba分词分析数据 5、支持数据导入导出 6、echarts展示图表 效果展示 演示链接 源码获取 int main(){ //非白嫖 printf("📡:%S","joyfelic"); return 0; }...

Spring Security架构中过滤器的实现
Spring Security过滤器基础 过滤器链工作原理 在Spring Security架构中,过滤器链(Filter Chain)是安全机制的核心实现方式。当HTTP请求到达时,会依次通过一系列具有明确顺序的过滤器。例如认证过滤器会拦截请求并将认证职责委托给授权管理器。若需要在认证前执行特定逻辑…...

Playwright Python API 测试:从入门到实践
Playwright Python API 测试:从入门到实践 在现代软件开发中,API 测试是确保应用程序后端功能正常运行的关键环节。Playwright 是一个强大的自动化测试工具,支持多种编程语言,其中包括 Python。通过 Playwright,我们可…...

ETL脚本节点使用的方式
随着大数据时代的到来,企业对数据处理的需求日益增长,ETL 作为数据整合的关键技术,逐渐走进我们的视野。本文将为您揭秘 ETL 脚本节点的使用方式,助您轻松驾驭数据处理新境界。 一、ETL脚本的优势 1.提高效率:ETL 脚…...

PH热榜 | 2025-06-02
1. Circuit Tracer 标语:Anthropic的开放工具:让我们了解AI是如何思考的 介绍:Anthropic的开源工具Circuit Tracer可以帮助研究人员理解大型语言模型(LLMs),它通过将内部计算可视化为归因图的方式展现相关…...
: A Comprehensive Review)
Domain Adaptation in Vision-Language Models (2023–2025): A Comprehensive Review
Domain Adaptation in Vision-Language Models (2023–2025): A Comprehensive Review Overview Recent research (2023–2025) has increasingly focused on adapting large Vision-Language Models (VLMs) to new domains and tasks with minimal supervision. A core tren…...
