算法:二分查找
1.二分查找
704. 二分查找 - 力扣(LeetCode)

二分查找算法要确定“二段性”,时间复杂度为O(lonN)。为了防止数据溢出,所以求mid时要用防溢出的方式。
class Solution {
public:int search(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while(left <= right){//int mid = (left + right) / 2;int mid = left + (right - left) / 2;//防溢出if(target > nums[mid]){left = mid + 1;}else if(target < nums[mid]){right = mid - 1;}else{return mid;}}return -1;}
};朴素二分模版
while(left <= right){int mid = left + (right - left) / 2;//防溢出if(......){left = mid + 1;}else if(......){right = mid - 1;}else{return ......;}}
2.在排序数组中查找元素的第一个和最后一个位置
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)

用二分查找解决,要查找一个区间要找去左端点和右端点。
1. 查找区间的左端点

细节处理:
1. 循环条件 left < right 而不是left <= right ,因为left == right 的时候就是最终结果,无需判断。如果判断了就会死循环(当left和right构成的区间中存在结果,并且 nums[mid] >= t时,此时mid也等于left和right,进行上述操作的时候会导致right = mid一直在原地,所以导致死循环)。
2. 求中点的操作
left + (right - left)/ 2 要向下取整,当剩两个点让mid的指针指向left。
2.查找区间右端点
与查找区间左端点的方法类似,只是处理条件不同。
1.当nums[mid] <= target 时left == mid。
2.当nums[mid] > target 时right == mid - 1。
循环条件:left < right 和上述原因一致。
求中点的方式 left + (right - left + 1) / 2 要向上取整,当剩两个点让mid的指针指向right。
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {if(nums.size() == 0)return {-1, -1};int left = 0, right = nums.size() - 1;int begin = 0;while(left < right)//确定区间的左端点{int mid = left + (right - left) / 2;//防溢出写法if(nums[mid] < target)left = mid + 1;elseright = mid;}//判断是否有结果if(nums[left] != target)return {-1,-1};elsebegin = left;left = 0, right = nums.size() - 1;while(left < right)//确定区间的右端点{int mid = left + (right - left + 1) / 2;if(nums[mid] <= target)left = mid;else right = mid - 1;}//如果存在左端点,那么右端点也一定存在,所以不用判断了,直接返回return {begin, right};}
};总结二分模版
while(left < right){int mid = left + (right - left) / 2;if(......)left = mid + 1;elseright = mid;}while(left < right)//确定区间的右端点{int mid = left + (right - left + 1) / 2;if(......)left = mid;else right = mid - 1;}3. 搜索插入位置
35. 搜索插入位置 - 力扣(LeetCode)

思路:二分查找,用左端点的模版,直接找到查找加返回要插入位置的值。如果未找到target,则检查target是否大于nums[right]:如果是,插入位置为right + 1;否则,插入位置为right(即第一个大于等于target的位置)。
class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while(left < right) {int mid = left + (right - left) / 2;if(nums[mid] < target)left = mid + 1;elseright = mid;}if(target > nums[right])return right + 1;elsereturn right;}
};4. x的平方根
69. x 的平方根 - 力扣(LeetCode)

直接将1 ~ x作为查找区间,找小于等于mid*mid的x的值
class Solution {
public:int mySqrt(int x) {if(x < 1) return 0;long long left = 0, right = x;while(left < right){long long mid = left + (right - left + 1) / 2;if(mid * mid <= x)left = mid;elseright = mid - 1;}return left;}
};5. 山脉数组的峰顶索引
852. 山脉数组的峰顶索引 - 力扣(LeetCode)

运用二分查找算法,因为在山脉数组中,在前一段山脉arr[mid] > arr[mid - 1],在后一段山脉arr[mid] < arr[mid - 1];根据这个二段性,使用二分查找。
class Solution {
public:int peakIndexInMountainArray(vector<int>& arr) {int left = 0, right = arr.size() - 1;while(left < right){int mid = left + (right - left + 1) / 2;if(arr[mid] > arr[mid - 1])left = mid;elseright = mid - 1;}return left;}
};6. 寻找峰值
162. 寻找峰值 - 力扣(LeetCode)

运用二分查找算法:对于区间中nums[i] 和 nums[i + 1],如果nums[i] < nums[i + 1],那么这段区间程上升趋势,因为nums[-1]和nums[n] = ,所以在后一段区间内一定有峰值,让left = mid + 1.
如果nums[i] > nums[i + 1],程下降趋势,在前一段区间内一定有峰值,让right = mid。
class Solution {
public:int findPeakElement(vector<int>& nums) {int left = 0, right = nums.size() - 1;while(left < right){int mid = left + (right - left) / 2;if(nums[mid] > nums[mid + 1])right = mid;elseleft = mid + 1;}return left;}
};7.寻找旋转排序数组中的最小值
153. 寻找旋转排序数组中的最小值 - 力扣(LeetCode)

思路:使用二分查找,因为这个数组是有二段性的(要找的值为第二段的第一个元素),将这个数组分为两段第一段的值一定比第二段的值大,所以根据nums[mid]和nums[n - 1]的关系作为比较。nums[mid]>nums[n - 1],说明在mid第一段,所以要让left = mid + 1;nums[mid] <= nums[n - 1]时,说明mid在第二段上,要让right = mid。
第二种方法是一nums[0]作为比较值,只是这种有特殊情况,全是升序的时候会导致mid一直向后走,所以找特殊判断一下升序的情况。
class Solution {
public:int findMin(vector<int>& nums) {/*int left = 0, right = nums.size() - 1, n = nums.size();while(left < right){int mid = left + (right - left) / 2;if(nums[mid] > nums[n - 1])left = mid + 1;elseright = mid;}return nums[right];*/int left = 0, right = nums.size() - 1, n = nums.size();if(nums[n - 1] > nums[0])return nums[0];while(left < right){int mid = left + (right - left) / 2;if(nums[mid] >= nums[0])left = mid + 1;elseright = mid;}return nums[right];}
};8.点名
LCR 173. 点名 - 力扣(LeetCode)

1.哈希表;2.直接遍历找结构;3.位运算;4.求和公式。这些方法的时间复杂度都是O(N)。
方法5:二分查找:这个数组有二段性,分成两段判断对应的值是否相等,还需要处理一下全升序的情况
class Solution {
public:int takeAttendance(vector<int>& records) {int left = 0, right = records.size() - 1, n = records.size();if(records[n - 1] == n - 1) return n;while(left < right){int mid = left + (right - left) / 2;if(records[mid] == mid)left = mid + 1;elseright = mid;}return right;}
};相关文章:

算法:二分查找
1.二分查找 704. 二分查找 - 力扣(LeetCode) 二分查找算法要确定“二段性”,时间复杂度为O(lonN)。为了防止数据溢出,所以求mid时要用防溢出的方式。 class Solution { public:int search(vector<int>& nums, int tar…...

Spring Boot3.4.1 集成 mybatis plus
Spring Boot 集成 mybatis plus 第一步 引入依赖 <dependency><groupId>mysql</groupId><artifactId>mysql-connector-java</artifactId><version>8.0.16</version> </dependency><dependency><groupId>com.bao…...

Ubuntu 22.04 上安装 PostgreSQL(使用官方 APT 源)
Ubuntu 22.04 上安装 PostgreSQL(使用官方 APT 源) 步骤 1:更新系统 sudo apt update sudo apt upgrade -y步骤 2:添加 PostgreSQL 官方仓库 # 安装仓库管理工具 sudo apt install wget ca-certificates gnupg lsb-release -y#…...

Linux随记(十八)
一、k8s的node节点磁盘 /data已使用率超过 85% , 出现disk pressure ,驱逐pod现象 evicted , the node had condition:[DiskPressure] #修改/var/lib/kubelet/config.yaml ]# cat /var/lib/kubelet/config.yaml apiVersion: kubelet.config.k8s.io/v1…...
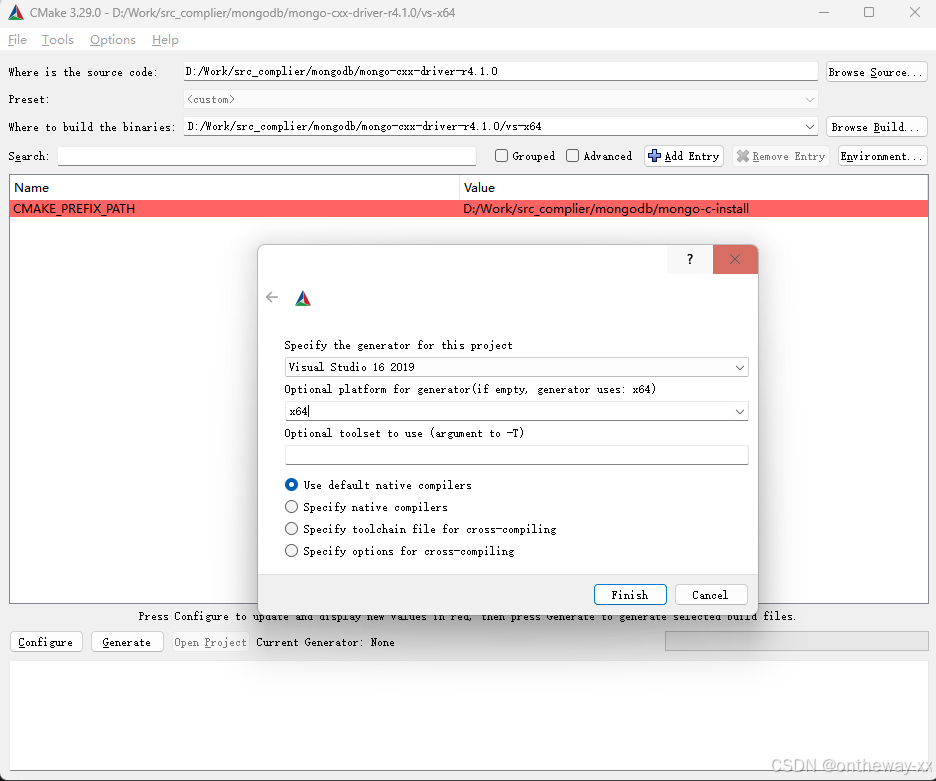
Windows MongoDB C++驱动安装
MongoDB驱动下载 MongoDB 官网MongoDB C驱动程序入门MongoDB C驱动程序入门 安装环境 安装CMAKE安装Visual Studio 编译MongoDB C驱动 C驱动依赖C驱动,需要先编译C驱动 下载MongoDB C驱动源码 打开CMAKE(cmake-gui) 选择源码及输出路径,然后点击configure …...
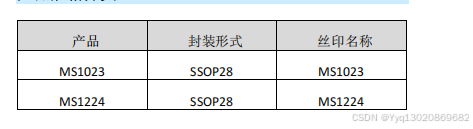
MS1023/MS1224——10MHz 到 80MHz、10:1 LVDS 并串转换器(串化器)/串并转换器(解串器)
产品简述 MS1023 串化器和 MS1224 解串器是一对 10bit 并串 / 串并转 换芯片,用于在 LVDS 差分底板上传输和接收 10MHz 至 80MHz 的并行字速率的串行数据。起始 / 停止位加载后,转换为负载编 码输出,串行数据速率介于 120Mbps…...

ESOP股权管理平台完整解决方案
——全生命周期合规化、智能化、价值化的资本中枢系统 一、平台顶层架构 1.1 四层驱动模型 #mermaid-svg-QrD0g5nIuRtsMl7c {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-QrD0g5nIuRtsMl7c .error-icon{fill:#552…...

线性调频波形测距测速信号处理——全代码+注释
clear all close all clc %% 参数设置 fs600e6;%采样率 fc10.45e9;% 波形发射载频 t10e-6;%脉宽 f050e6;%波形中频频率 B10e6;%带宽 uB/(2*t);%调频斜率 Tv100e-6;% 脉冲重复周期 Num64;% 测速脉冲数 lamdfs/B;% 抽取带宽 Nsround(fs*t); NTvround(fs*Tv); tt0:1/fs:t-1/fs; ff…...

WPS word 已有多级列表序号
wps的word中,原来已生成的文档里,已存在序号。比如,存在2、2.1、2.1.1、2.1.1.1、2.1.1.1.1 5层序号,而且已分为5级。但增加内容的时候,并不会自动增加序号,应该如何解决? 原来长这样ÿ…...
)
Vue 3 源码层核心原理剖析(完整详解版)
一、Compiler 编译过程解密:多框架实现对比 Vue 3 编译流程深度解析(基于 /packages/compiler-core/src/parse.ts) 完整编译链条及技术实现: #mermaid-svg-S8ScpxdjkcJv0YWT {font-family:"trebuchet ms",verdana,ari…...
)
数据库操作-MySQL-4(JDBC编程)
JDBC:通过Java代码操作mysql数据库,数据库会提供一些API供我们调用 MySQL、Oracle、等API有差异,但是Java统一了所有接口,即JDBC; 原始api-驱动包(类似转接头)-统一的api-Java 驱动包࿱…...

Linux打开.img镜像文件
kparkx 可以查看和修改img文件的内容 1.安装kparkx 1.安装 kpartx sudo apt-get update sudo apt-get install kpartx2.使用kpartx映射镜像文件 假设镜像文件名为 example.img ,以下命令会将其分区映射到 dev/mapper/ sudo kpartx -av example.img• -a表示添加…...
)
【FAQ】HarmonyOS SDK 闭源开放能力 —Account Kit(5)
1.问题描述: 集成华为一键登录的LoginWithHuaweiIDButton, 但是Button默认名字叫 “华为账号一键登录”,太长无法显示,能否简写成“一键登录”与其他端一致? 解决方案: 问题分两个场景: 一、…...
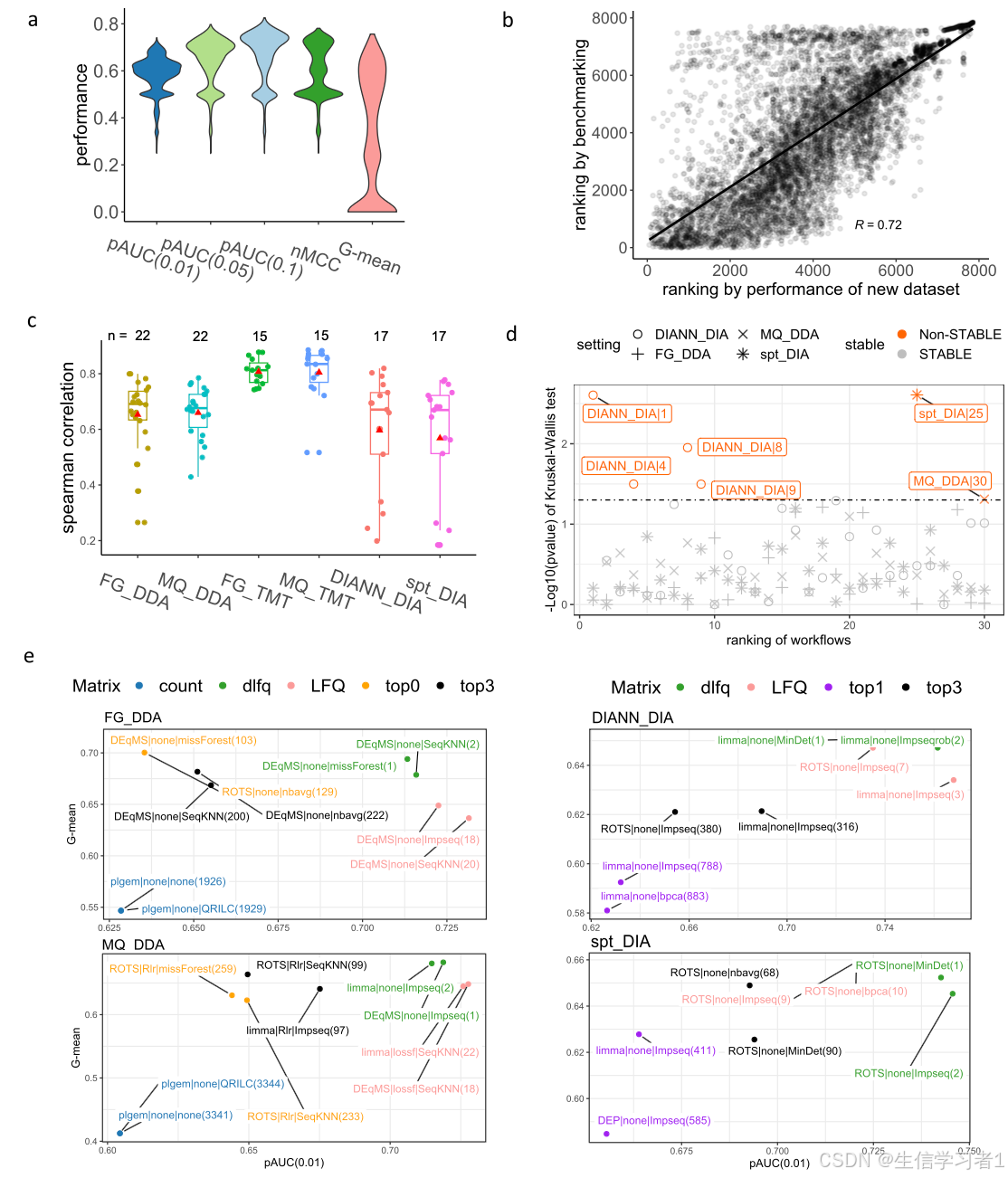
【科研绘图系列】R语言绘制论文组合图形(multiple plots)
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍加载R包数据下载导入数据数据预处理画图1画图2画图3画图4画图5系统信息介绍 这篇文章详细介绍了如何使用R语言进行科研绘图,特别是绘制论文组合图形(multiple plots)。文章从数…...

springMVC-9数据格式化
数据格式化 学习目标: 理解在我们提交数据(比如表单时),SpringMVC怎样对提交的数据进行转换和处理的 Spring MVC 上下文中内建了很多转换器,可完成大多数 Java 类型的转换工作。 基本数据类型可以和字符串之间自动完成转换 应用实例-页面…...

Kafka 和Redis 在系统架构中的位置
Kafka 位置:位于应用层和数据存储层之间,作为消息队列和数据传输中间件。作用: 数据收集与传输:收集应用层产生的数据,传输到后端数据存储系统。消息队列:实现应用层各服务之间的异步通信和解耦。与应用层…...

【Spring AI】如何实现文生图功能
在人工智能与软件开发深度融合的当下,Spring AI 作为构建 AI 驱动应用的有力框架,能够便捷集成各类 AI 能力。 文生图技术可将文本描述转化为图像,极具应用价值。接下来,我给大家详细讲解一下如何使用 Spring AI 调用文生图功能。…...

【ISAQB大纲解读】Kafka消息总线被视为“自下而上设计”?
Kafka消息总线被视为“自下而上设计”的典型案例,核心在于其设计路径和演化逻辑完全符合自下而上方法的本质特征: 自下而上设计的核心逻辑 #mermaid-svg-pDSqW0S2h0bj15iN {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16…...

ISBN书号查询接口如何用PHP实现调用?
一、什么是ISBN书号查询接口 ISBN数据查询接口是一项图书信息查询服务。它基于全球通用的ISBN编码系统,帮助用户快速获取图书的详细信息,包括书名、作者、出版社、出版时间、价格、封面等关键字段。 该接口广泛应用于电商平台、图书馆管理系统、二手书…...
,为什么你需要它,它是怎么工作的)
什么是 Docker Compose 的网络(network),为什么你需要它,它是怎么工作的
Docker Compose 的网络就是:让多个容器之间能像“连上同一个局域网”一样互相通信,不用管 IP,用服务名就能访问彼此。 就像家里连接到同一个 WiFi 的手机、电脑、电视,它们都能互相发现对方,Docker 里的容器也是一样 …...
)
嵌入式Linux 期末复习指南(上)
鉴于互联网上针对本科目相关复习视频及资料过少, 撰写本篇期末复习指南用作期末复习知识点扫盲,以应对本科期末考试及格之用。 由于任课老师并透露考试范围或任何有关试卷的相关信息,本篇指南基于教材、上机实验报告及作者经验编写࿰…...

SpringBoot3.2新特性:JdbcClient
文章目录 一、简介二、使用1、支持隐式位置参数2、通过索引设置位置参数3、支持 Name / Value 对命名参数4、通过 Map 设置命名参数5、使用 JdbClient 执行更新操作6、使用示例 参考资料 一、简介 Spring 6.1 中新添加了 JdbcClient 接口,它提供了 Fluent 风格的 A…...

Dify:启动 Web 服务的详细指南
1. 进入 web 目录 cd web解释: cd 是 “change directory” 的缩写,用于切换当前工作目录。您需要进入项目的 web 目录,这是前端代码所在的位置。在这个目录下,您可以执行构建和启动 Web 服务的相关命令。 2. 安装依赖 pnpm in…...

3.1 HarmonyOS NEXT分布式数据管理实战:跨设备同步、端云协同与安全保护
HarmonyOS NEXT分布式数据管理实战:跨设备同步、端云协同与安全保护 在万物互联的时代,数据的跨设备流转与安全共享是全场景应用的核心需求。HarmonyOS NEXT通过分布式数据管理技术,实现了设备间数据的实时同步与端云协同,为开发…...

Aop + 注解实现数据字典类型转换 EasyExcel导出
Aop 注解 实现数据字典类型转换 文章目录 Aop 注解 实现数据字典类型转换一、基础方式✅字典转换简介👉实现步骤✅ 1. 定义自定义注解Dict ✅ 2. 定义查询字典项的两个方法✅ 3. 定义Aop拦截我们查询的方法✅ 4. VO映射类✅ 5. Controller层✅ 6. serviceImpl✅ 7. …...

Python 元组方法全集详解
Python 元组方法全集详解 在 Python 中,元组(tuple)是不可变序列类型,因此支持的操作比列表少。以下是元组支持的所有方法和操作: 一、元组核心方法 1. 创建元组 # 标准创建 t = (1, 2, 3) # (1, 2, 3) t = tuple(...

Selenium 中 JavaScript 点击操作的原理及应用
在 Selenium 中使用 JavaScript 执行点击操作(如 driver.execute_script("arguments[0].click();", element))的原理涉及 WebDriver 架构、浏览器事件机制以及 JavaScript 对 DOM 的直接操作,以下是详细解释: 1. Selen…...

Xilinx超过256m bit flash固件跳转失败问题
问题描述 按照 链接: Xilinx 7系列fpga在线升级和跳转 这个方式跳转失败 问题排查 进一步排查现象如下 上面这个现象呈现出明显的以16m为周期的规律。感觉很大概率是因为flash超过了16m(256bit)导致的地址越界问题。另外我在CSDN上也找到类似的问题…...

SpringCloud 分布式锁Redisson锁的重入性与看门狗机制 高并发 可重入
可重入 Redisson 的锁支持 可重入性,这意味着同一个线程在获取锁后,如果再次尝试获取该锁,它可以成功地获得锁,而不会被阻塞。 每次一个线程成功获取锁后,它的持有次数会增加。当线程再次获取该锁时,Redi…...

02 APP 自动化-Appium 运行原理详解
环境搭建见 01 APP 自动化-环境搭建 文章目录 一、Appium及Appium自动化测试原理二、Appium 自动化配置项三、常见 ADB 命令四、第一个 app 自动化脚本 一、Appium及Appium自动化测试原理 Appium 跨平台、开源的 app 自动化测试框架,用来测试 app 应用程序&#x…...
