经典算法回顾之最小生成树
最小生成树(Minimum Spanning Tree,简称MST)是图论中的一个重要概念,主要用于解决加权无向图中连接所有顶点且总权重最小的树结构问题。本文对两种经典的算法即Prim算法和Kruskal算法进行回顾,并对后者的正确性给出简单的证明。
一. 定义
最小生成树是给定连通加权无向图 G = ( V , E ) G = (V, E) G=(V,E) 中的一棵生成树,满足以下条件:
- 包含所有顶点:生成树覆盖了图中的所有顶点。
- 边权之和最小:生成树中所有边的权重之和最小。
- 无环性:生成树中不包含任何环路。
形式化定义:假设 T T T 是 E E E 的一个子集,且 ( V , T ) (V, T) (V,T) 是一棵树,使得 w ( T ) w(T) w(T)(即 T T T 中所有边的权重之和)最小,则 T T T 为 G G G 的最小生成树。
二. 基本概念
- 割:将图 G G G 的顶点集分为不相交的两部分,假设一个子集为 U U U, 则另一子集为 V − U V-U V−U。如下图所示: U = { 0 , 4 , 5 } , V − U = { 1 , 2 , 3 , 6 } U=\{0,4,5\},V-U=\{1,2,3,6\} U={0,4,5},V−U={1,2,3,6}。
- 跨边:穿过割的边称为跨边。如下图所示: ( 0 , 1 ) , ( 4 , 6 ) , ( 4 , 3 ) (0,1),(4,6),(4,3) (0,1),(4,6),(4,3) 为这一割的3条跨边。

三. 基本性质
性质1:若 ( u , v ) (u,v) (u,v) 是某一割的最短跨边,那么必然存在一棵MST包含 ( u , v ) (u,v) (u,v)。
推论1:若 ( u , v ) (u,v) (u,v) 不是任意割的最短跨边,那么任意MST均不包含它。
推论2:任意一棵MST也必然包含任意割的最短跨边 ( u , v ) (u,v) (u,v)。
反证法证明性质1:
如下图所示,假设 ( u , v ) (u,v) (u,v) 未被任何MST采用,那么任取一棵MST,连接 ( u , v ) (u,v) (u,v) 必然会构成唯一的回路,且该回路必然包含 ( u , v ) (u,v) (u,v) 以及另一条跨边 ( s , t ) (s,t) (s,t)。 此时,若断开 ( s , t ) (s,t) (s,t), 那么我们将得到一棵新的生成树,且权重之和更小,于是我们得到了更小的MST。 这与假设不符,因此,若 ( u , v ) (u,v) (u,v) 是某一割的最短跨边,那么必然存在一棵MST包含 ( u , v ) (u,v) (u,v)

四. Prim算法
4.1 Prim算法描述
从 T 1 = ( { v 1 } ; ∅ ) T_1 = (\{v_1\}; \varnothing) T1=({v1};∅) 开始,逐步构造 T 2 、 T 3 、 . . . 、 T n T_2、T_3、...、T_n T2、T3、...、Tn。其中, v 1 v_1 v1 可以任选。
T k = ( V k ; E k ) , ∣ V k ∣ = k , ∣ E k ∣ = k − 1 , V k ⊂ V k + 1 T_k = (V_k; E_k),|V_k| = k,|E_k| = k-1,V_k \subset V_{k+1} Tk=(Vk;Ek),∣Vk∣=k,∣Ek∣=k−1,Vk⊂Vk+1。
由以上分析,为由 T k T_k Tk 构造 T k + 1 T_{k+1} Tk+1 ,
只需将 ( V k : V − V k ) (V_k : V-V_k) (Vk:V−Vk) 视作原图的一个割, 并在该割的所有跨边中,
找出极短者 e k = ( v k , u k ) e_k = (v_k, u_k ) ek=(vk,uk) ,
则 T k + 1 = ( V k + 1 ; E k + 1 ) = ( V k ∪ u k ; E k ∪ e k ) T_{k+1} = (V_{k+1}; E_{k+1}) = (V_k \cup {u_k}; E_k \cup {e_k} ) Tk+1=(Vk+1;Ek+1)=(Vk∪uk;Ek∪ek) 。
4.2 Prim算法示例

4.3 Prim算法代码
#define INF 32767 //INF表示∞, 邻接矩阵中不可达边的权重为∞
int dis[1000], inMST[1000], mst = 0; //dis: V-U 到 U的最短距离 mst: 最小生成树的权重和void Prim(vector<vector<int>>& G, int v){inMST[v] = 1;for (int i = 0; i < G.size(); i++) dis[i] = G[v][i];for (int i = 1; i < G.size(); i++) { //循环n-1次int min = INF, k;for (int j = 0; j < G.size(); j++) //在(V-U)中找出离U最近的顶点kif (inMST[j] == 0 && dis[j] < min)min = dis[j], k = j; // min: 最短距离,k:最近顶点编号mst += min;inMST[k] = 1; //标记k已经被加入for (int j = 0; j < G.size(); j++) //更新其它点到U的距离if (inMST[j] == 0 && G[k][j] < dis[j])dis[j] = G[k][j];}
}
五. Kruskal算法
5.1 算法描述
- 将图 G = ( V , E ) G = (V, E) G=(V,E) 中的所有边按权重非降序排序。设排序后的边序列为 e 1 , e 2 , . . . , e ∣ E ∣ e_1, e_2, ..., e_{|E|} e1,e2,...,e∣E∣。
- 初始化一个空的边集 T = { } T = \{\} T={},用于存放 MST 的边。
- 按排序后的顺序 ( i = 1 i = 1 i=1 到 ∣ E ∣ |E| ∣E∣),依次考虑每条边 e i e_i ei:
- 如果将 e i e_i ei 加入 T T T 后, T T T 中不会形成环,则将 e i e_i ei 加入 T T T ( T = T ∪ { e i } T = T ∪ \{e_i\} T=T∪{ei})。
- 否则(即加入 e i e_i ei 会形成环),丢弃 e i e_i ei。
- 当 T T T 中包含 ∣ V ∣ − 1 |V| - 1 ∣V∣−1 条边时,算法终止。 T T T 即为所求的 MST。
5.2 Kruskal算法示例

5.3 Kruskal算法代码
int parent[maxn], mst_w;
struct Edge { int from, to, w; } edges[maxn];
bool compare(Edge e1, Edge e2) { return e1.w <= e2.w; }int Find(int x) { //查找结点x的根(集合代表) if (x == parent[x]) //找到根return x; //返回根(集合代表) elsereturn parent[x] = Find(parent[x]); //递归向上找根
}void Union(int x,int y) { //合并x和y所在的集合int px = Find(x);int py = Find(y);if (px != py) //如果两个集合不同则合并 parent[px] = py;
}int Kruskal(int en) { for (int i = 0; i < maxn; i++) parent[i] = i; //初始化并查集sort(edges, edges + en, compare); for (int i = 0; i < en; i++) {int p1 = Find(edges[i].from);int p2 = Find(edges[i].to);if (p1 != p2) {Union(p1, p2);mst_w += edges[i].w;}}return mst_w;
}
5.4 Kruskal算法正确性证明
接下来,简单证明一下这个算法的正确性。本文的证明方式跟绝大多数书上和网上的证明方式不同,证明主要基于上面提到的一个性质和两个推论:
性质1:若 ( u , v ) (u,v) (u,v) 是某一割的最短跨边,那么必然存在一棵MST包含 ( u , v ) (u,v) (u,v)。
推论1:若 ( u , v ) (u,v) (u,v) 不是任意割的最短跨边,那么任意MST均不包含它。(性质1的逆否命题)
推论2:任意一棵MST也必然包含任意割的最短跨边 ( u , v ) (u,v) (u,v)。
为了证明Kruskal算法的正确性,需要证明两点:
- 因为构成了回路而放弃的边不属于任意MST。
- 按照边长顺序加入的边必然都属于某棵MST。
1)首先证明:因为构成了回路而放弃的边不属于任意MST。
首先,如果一个图中的所有边的权重都不相同时,这个图对应的MST是唯一的。这一点不难证明,因为在Prim算法中,每一步都只能选择唯一的一条最短跨边。但图中确实可能存在权重相同的边,处理方式也很简单,就是对边的权重做稍微扰动(针对某条边,扰动后要保证,权重原本比它小的边扰动后依然比它小,权重原本比它大的边扰动后依然比它大,即不改变相对顺序),使之各不相同,那么MST也是唯一的。
这里我们就假设给定图 G = ( V , E ) G = (V, E) G=(V,E) 的所有边的权重均不相同。
在Kruskal算法中,因为构成了回路而放弃的一些边。 我们说这些边不属于MST。
如下图所示,假设在Kruskal算法的某一步,我们将边 e k = ( v i , v j ) e_k=(v_i,v_j) ek=(vi,vj) 加入之后,在局部构成了回路。

在这个回路中(上图红色的边), e k = ( v i , v j ) e_k=(v_i,v_j) ek=(vi,vj) 是最后加入的边,因此它是这个回路中权重最大的边。
进一步,如果将 e k = ( v i , v j ) e_k=(v_i,v_j) ek=(vi,vj) 作为一个跨边 (即将 v i v_i vi 和 v j v_j vj 放到两个不相交的子集中),我们发现这个割无论如何都会穿过这个回路中的其它边。
又因为其他边的权重都大于 e k e_k ek, 因此 e k e_k ek 是不是任意割的最短跨边。
所以 e k e_k ek 不包含在MST中。
2)然后证明:按照边长顺序加入的边必然都属于某棵MST。
不失一般性,如下图所示,我们仍然假设接下来考查的是 e k = ( v i , v j ) e_k=(v_i,v_j) ek=(vi,vj)。它是否在MST中呢? 只要它在某一割的最短跨边,那么它就在MST中。

我们要将 e k = ( v i , v j ) e_k=(v_i,v_j) ek=(vi,vj) 构造为一个最短跨边,就要构造一个割,且这一割不经过别的更短的跨边(也就是不穿过那些已经在MST中的跨边)。为此,我么可以将那些已经在MST子树中的点缩点即可,这样割就不会穿过比 e k = ( v i , v j ) e_k=(v_i,v_j) ek=(vi,vj) 更短的跨边了。
如下图所示,缩点后,图中仅剩3个点,我们可以很容易的构造一个割将 v i v_i vi 和 v j v_j vj 放到两个不相交的子集中。且 e k = ( v i , v j ) e_k=(v_i,v_j) ek=(vi,vj) 是该割的最短跨边,尽管可能还有其它跨边,但是Kruskal算法是按顺序遍历的边,所有还未遍历到的边的权重必然大于 e k = ( v i , v j ) e_k=(v_i,v_j) ek=(vi,vj)。

为此,Kruskal算法的正确性得证。
六. Prim算法 和 Kruskal算法的局限性
我们一般讲最小生成树,只针对无向图,对于有向图是有问题的,如下图所示。

有向图的最小生成树->最小树形图: https://oi-wiki.org/graph/dmst/
参考资料
邓俊辉,数据结构(C++语言版),清华大学出版社
相关文章:

经典算法回顾之最小生成树
最小生成树(Minimum Spanning Tree,简称MST)是图论中的一个重要概念,主要用于解决加权无向图中连接所有顶点且总权重最小的树结构问题。本文对两种经典的算法即Prim算法和Kruskal算法进行回顾,并对后者的正确性给出简单…...

Ubuntu下实现nginx反向代理
1. 多个ngx实例安装 脚本已经在deepseek的指导下完成啦! deepseek写的脚本支持ubuntu/centos两种系统。 ins_prefix"/usr/local/" makefile_gen() {ngx$1 ngx_log_dir"/var/log/"$ngx"/"ngx_temp_path"/var/temp/"${ngx}…...

c++ QicsTable使用实例
效果图: #include <QicsTable.h> #include <QicsDataModelDefault.h> #include <QVBoxLayout> Demo1::Demo1(QWidget *parent) : QWidget(parent) { ui.setupUi(this); const int numRows 10; const int numCols 5; // create th…...

在WordPress上添加隐私政策页面
在如今的互联网时代,保护用户隐私已经成为每个网站管理员的责任。隐私政策不仅是法律要求,还能提高用户对网站的信任。本文将介绍两种常用方法,帮助你在WordPress上轻松创建并发布隐私政策页面。这些方法简单易行,符合中国用户的阅…...

二维 根据矩阵变换计算镜像旋转角度
在二维变换中,镜像(Reflection) 是一种特殊的线性变换,它会将图形对称地翻转到某个轴线或点。镜像的存在会显著影响圆弧变换后的参数(圆心、半径、起始角度),尤其是在角度方向和旋转方向的处理上…...

你工作中涉及的安全方面的测试有哪些怎么回答
在面试或工作总结中,回答 **“工作中涉及的安全测试”** 时,可以结合具体场景、测试方法和工具,突出你的技术广度和深度。以下是结构化回答建议: --- ### **1. 分类说明安全测试范围** #### **(1) Web 应用安全测试** - **OWASP…...

阿里云ACP云计算备考笔记 (3)——云服务器ECS
目录 第一章 整体概览 第二章 ECS简介 1、产品概念 2、ECS对比本地IDC 3、BGP机房优势 第三章 ECS实例 1、实例规格族 2、实例系列 3、应用场景推荐选型 4、实例状态 5、创建实例 ① 完成基础配置 ② 完成网络和安全组配置 ③ 完成管理配置和高级选项 ④ 确认下单…...

Eigen实现非线性最小二乘拟合 + Gauss-Newton算法
下面是使用 Eigen 实现的 非线性最小二乘拟合 Gauss-Newton 算法 的完整示例,拟合模型为: 拟合目标模型: y exp ( a x 2 b x c ) y \exp(a x^2 b x c) yexp(ax2bxc) 已知一组带噪声数据点 ( x i , y i ) (x_i, y_i) (xi,yi)&…...

区块链技术:原理、应用与发展趋势
区块链技术:原理、应用与发展趋势 引言 区块链作为一种去中心化的分布式账本技术,自2008年比特币白皮书发布以来,已经从简单的加密货币底层技术发展成为具有广泛应用前景的创新技术。区块链通过独特的数据结构和加密机制,实现了…...

从零开始:用Tkinter打造你的第一个Python桌面应用
目录 一、界面搭建:像搭积木一样组合控件 二、菜单系统:给应用装上“控制中枢” 三、事件驱动:让界面“活”起来 四、进阶技巧:打造专业级体验 五、部署发布:让作品触手可及 六、学习路径建议 在Python生态中&am…...

Web开发主流前后端框架总结
🖥 一、前端主流框架 前端框架的核心是提升用户界面开发效率,实现高交互性应用。当前三大主流框架各有侧重: React (Meta/Facebook) 核心特点:采用组件化架构与虚拟DOM技术(减少真实DOM操作,优化渲染性能&…...

Java Spring Boot 自定义注解详解与实践
目录 一、自定义注解的场景与优势1.1 场景1.2 优势 二、创建自定义注解2.1 定义注解2.2 创建注解处理器 三、使用自定义注解3.1 在业务方法上使用注解3.2 配置类加载注解 四、总结 在 Spring Boot 中,自定义注解为我们提供了一种灵活且强大的方式来简化开发、增强代…...

GlobalSign、DigiCert、Sectigo三种SSL安全证书有什么区别?
GlobalSign、DigiCert和Sectigo是三家知名的SSL证书颁发机构,其产品在安全性、功能、价格和适用场景上存在一定差异。选择SSL证书就像为你的网站挑选最合身的“安全盔甲”,核心是匹配你的实际需求,避免过度配置或防护不足。 一、核心特点对…...

力扣面试150题--二叉搜索树中第k小的元素
Day 58 题目描述 思路 直接采取中序遍历,不过我们将k参与到中序遍历中,遍历到第k个元素就结束 /*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* …...

SQL Server Agent 不可用怎么办?
在 SQL Server Management Studio (SSMS) 中,SQL Server Agent 通常位于对象资源管理器(Object Explorer)的树形结构中,作为 SQL Server 实例的子节点。以下是详细说明和可能的原因: 1. SQL Server Agent 的位置 默认路…...

css-塞贝尔曲线
文章目录 1、定义2、使用和解释 1、定义 cubic-bezier() 函数定义了一个贝塞尔曲线(Cubic Bezier)语法:cubic-bezier(x1,y1,x2,y2) 2、使用和解释 x1,y1,x2,y2,表示两个点的坐标P1(x1,y1),P2(x2,y2)将以一条直线放在范围只有 1 的坐标轴中,并…...

Java并发编程哲学系列汇总
文章目录 并发编程基础并发编程进阶并发编程实践 并发编程基础 Java并发编程基础小结 Java线程池知识点小结 详解JUC包下各种锁的使用 并发编程利器Java CAS原子类全解 深入理解Java中的final关键字 Java并发容器深入解析:HashMap与ArrayList线程安全问题及解…...

docker使用proxy拉取镜像
前提条件,宿主机可以访问docker hub 虚拟机上telnet 宿主机7890能正常访问 下面的才是关键,上面部分自己想办法~ 3. 编辑 /etc/docker/daemon.json {"proxies": {"http-proxy": "http://192.168.100.1:7890","ht…...

服务端定时器的学习(一)
一、定时器 1、定时器是什么? 定时器不仅存在于硬件领域,在软件层面(客户端、网页和服务端)也普遍应用,核心功能都是高效管理大量延时任务。不同应用场景下,其实现方式和使用方法有所差异。 2、定时器解…...

【前端】vue 防抖和节流
在 Vue.js 中,防抖(Debounce) 和 节流(Throttle) 是优化高频事件(如输入、滚动、点击)的核心技术,可显著提升性能与用户体验。以下是具体实现方法和最佳实践: ⏳ 一、防抖…...

Modbus转EtherNET IP网关开启节能改造新范式
在现代工业生产和能源管理中,无锡耐特森Modbus转EtherNET IP网关MCN-EN3001发挥着至关重要的作用。通过将传统的串行通信协议Modbus转换为基于以太网的EtherNET IP协议,这种网关设备不仅提高了数据传输的效率,而且为能源管理和控制系统的现代…...

Android高级开发第四篇 - JNI性能优化技巧和高级调试方法
文章目录 Android高级开发第四篇 - JNI性能优化技巧和高级调试方法引言为什么JNI性能优化如此重要?第一部分:JNI性能基础知识JNI调用的性能开销何时使用JNI才有意义? 第二部分:核心性能优化技巧1. 减少JNI调用频率2. 高效的数组操…...

【PCB工艺】绘制原理图 + PCB设计大纲:最小核心板STM32F103ZET6
绘制原理图和PCB布线之间的联系,在绘制原理图的时候,考虑到后续的PCB设计+嵌入式软件代码的业务逻辑,需要在绘制原理图之初涉及到 硬件设计流程的前期规划。在嵌入式系统开发中,原理图设计是整个项目的基础,直接影响到后续的: PCB 布线效率和质量 ☆☆☆重点嵌入式软件的…...

C#入门学习笔记 #7(传值/引用/输出/数组/具名/可选参数、扩展方法(this参数))
欢迎进入这篇文章,文章内容为学习C#过程中做的笔记,可能有些内容的逻辑衔接不是很连贯,但还是决定分享出来,由衷的希望可以帮助到你。 笔记内容会持续更新~~ 本篇介绍各种参数,参数本质上属于方法的一部分,所以本篇算是对方法更深度的学习。本章难度较大... 传值参数 …...

【DeepSeek】【Dify】:用 Dify 对话流+标题关键词注入,让 RAG 准确率飞跃
1 构建对话流处理数据 初始准备 文章大纲摘要 数据标注和清洗 代码执行 特别注解 2 对话流测试 准备工作 大纲生成 清洗片段 整合分段 3 构建知识库 构建 召回测试 4 实战应用测试 关键词提取 智能总结 测试 1 构建对话流处理数据 初始准备 构建对话变量 用…...

DELETE 与 TRUNCATE、DROP 的区别
DELETE 与 TRUNCATE、DROP 的区别 1. 基本概念 1.1 DELETE DELETE 是标准的 DML(数据操作语言) 命令,用于从表中删除特定行或所有行数据,但保留表结构。 go专栏:https://duoke360.com/tutorial/path/golang 1.2 TRUNCATE TRUNCATE 是 DDL(数据定义语言) 命令,用于快速…...
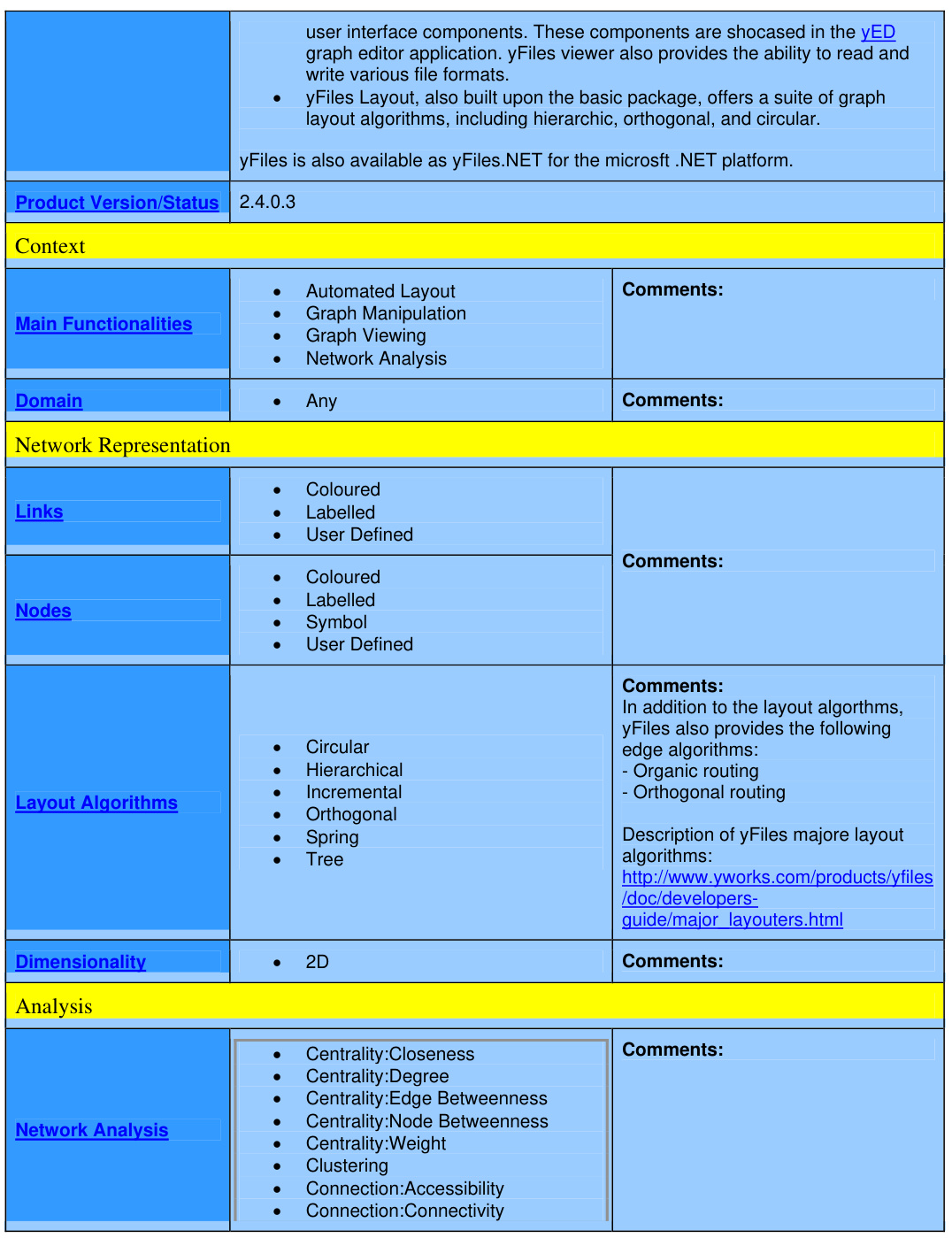
yFiles:专业级图可视化终极解决方案
以下是对yFiles的详细介绍,结合其定义、功能、技术特点、应用场景及行业评价等多维度分析: 一、yFiles的定义与核心定位 yFiles是由德国公司yWorks GmbH开发的 动态图与网络可视化软件开发工具包(SDK) ,专注于帮助用户将复杂数据转化为交互式图表。其核心价值在于提供跨平…...

VSCode 工作区配置文件通用模板创建脚本
下面是分别使用 Python 和 Shell(Bash)脚本 自动生成 .vscode 文件夹及其三个核心配置文件(settings.json、tasks.json、launch.json)的完整示例。 你可以选择你熟悉的语言版本来使用,非常适合自动化项目初始化流程。…...

echarts显示/隐藏标签的同时,始终显示饼图中间文字
显示标签的同时,始终显示饼图中间文字 let _data this.chartData.slice(1).map((item) > ({name: item.productName,value: Number(item.stock), })); this.chart.setOption({tooltip: {trigger: item,},graphic: { // 重点在这里(显示饼图中间文字&…...

【Spring AI】调用 DeepSeek 实现问答聊天
文章目录 一、基础概念解析1.Spring AI 框架2.DeepSeek 模型 二、开发环境搭建1.JDK 环境准备2.开发工具选择 三、项目创建与依赖添加1.创建 Spring Boot 项目2.DeepSeek API 四、代码编写实现调用1.创建问答服务类2.创建 Controller 类3.前端调用示例 五、项目运行与调试 在人…...
