贪心算法应用:装箱问题(BFD算法)详解

贪心算法应用:装箱问题(BFD算法)详解
1. 装箱问题与BFD算法概述
1.1 装箱问题定义
装箱问题(Bin Packing Problem)是组合优化中的经典问题,其定义为:
- 给定n个物品,每个物品有大小wᵢ (0 < wᵢ ≤ C)
- 无限数量的箱子,每个箱子容量为C
- 目标:用最少数量的箱子装下所有物品
1.2 BFD算法简介
最佳适应递减算法(Best Fit Decreasing, BFD)是解决装箱问题的高效启发式算法:
- 先将所有物品按大小降序排序
- 然后对每个物品,将其放入能容纳它且剩余空间最小的箱子
- 若无合适箱子,则开启新箱子
与FFD的区别:
- FFD选择第一个能装下物品的箱子
- BFD选择最适合(剩余空间最小)的箱子
2. BFD算法详细解析
2.1 算法思想
BFD算法的核心思想是:
- 排序阶段:大物品优先处理,减少碎片空间
- 放置阶段:每次选择最合适的箱子,提高空间利用率
2.2 算法步骤
- 输入:物品列表items,箱子容量C
- 排序:将items按非递增顺序排序
- 初始化:创建空箱子列表bins
- 分配物品:
- 对于每个物品item:
- 遍历所有箱子,找到满足条件且剩余空间最小的箱子
- 若找到,放入该箱子
- 若未找到,创建新箱子并放入
- 对于每个物品item:
- 输出:使用的箱子列表
2.3 伪代码表示
function BFD(items, C):sortedItems = sortDescending(items)bins = []for item in sortedItems:bestBin = nullminSpace = C + 1 // 初始化为大于最大可能值for bin in bins:space = C - bin.currentWeightif space >= item and space < minSpace:bestBin = binminSpace = spaceif bestBin != null:bestBin.add(item)else:newBin = new Bin(C)newBin.add(item)bins.add(newBin)return bins
3. Java实现BFD算法
3.1 基础实现
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;public class BinPackingBFD {public static void main(String[] args) {List<Integer> items = List.of(4, 8, 5, 1, 2, 3, 6, 7, 9, 4);int binCapacity = 10;List<List<Integer>> bins = bestFitDecreasing(items, binCapacity);printBins(bins);}public static List<List<Integer>> bestFitDecreasing(List<Integer> items, int binCapacity) {// 复制并排序物品列表List<Integer> sortedItems = new ArrayList<>(items);Collections.sort(sortedItems, Collections.reverseOrder());List<List<Integer>> bins = new ArrayList<>();List<Integer> binCapacities = new ArrayList<>(); // 跟踪每个箱子的已用容量for (int item : sortedItems) {// 寻找最佳箱子int bestBinIndex = -1;int minRemaining = binCapacity + 1; // 初始化为不可能的值for (int i = 0; i < bins.size(); i++) {int remaining = binCapacity - binCapacities.get(i);if (remaining >= item && remaining < minRemaining) {bestBinIndex = i;minRemaining = remaining;}}// 放置物品if (bestBinIndex != -1) {bins.get(bestBinIndex).add(item);binCapacities.set(bestBinIndex, binCapacities.get(bestBinIndex) + item);} else {List<Integer> newBin = new ArrayList<>();newBin.add(item);bins.add(newBin);binCapacities.add(item);}}return bins;}private static void printBins(List<List<Integer>> bins) {System.out.println("使用的箱子数量: " + bins.size());for (int i = 0; i < bins.size(); i++) {List<Integer> bin = bins.get(i);int sum = bin.stream().mapToInt(Integer::intValue).sum();System.out.printf("箱子 %d: %s (总大小: %d)%n", i+1, bin, sum);}}
}
3.2 面向对象优化实现
import java.util.*;public class BinPackingBFDAdvanced {public static void main(String[] args) {List<Integer> items = List.of(4, 8, 5, 1, 2, 3, 6, 7, 9, 4);int binCapacity = 10;BinPackingResult result = packItemsBFD(items, binCapacity);result.printBins();}static class Bin {private final int capacity;private final List<Integer> items;private int currentWeight;public Bin(int capacity) {this.capacity = capacity;this.items = new ArrayList<>();this.currentWeight = 0;}public boolean canAdd(int item) {return currentWeight + item <= capacity;}public void addItem(int item) {if (!canAdd(item)) {throw new IllegalStateException("超出箱子容量");}items.add(item);currentWeight += item;}public int getRemainingCapacity() {return capacity - currentWeight;}public List<Integer> getItems() {return Collections.unmodifiableList(items);}public int getCurrentWeight() {return currentWeight;}}static class BinPackingResult {private final List<Bin> bins;private final int binCapacity;public BinPackingResult(List<Bin> bins, int binCapacity) {this.bins = bins;this.binCapacity = binCapacity;}public void printBins() {System.out.println("使用的箱子数量: " + bins.size());System.out.printf("平均填充率: %.2f%%%n", getAverageFillRate() * 100);for (int i = 0; i < bins.size(); i++) {Bin bin = bins.get(i);System.out.printf("箱子 %2d: %s (总大小: %2d, 填充率: %5.2f%%)%n",i+1, bin.getItems(), bin.getCurrentWeight(),(double)bin.getCurrentWeight() / binCapacity * 100);}}public double getAverageFillRate() {return bins.stream().mapToDouble(bin -> (double)bin.getCurrentWeight() / binCapacity).average().orElse(0);}}public static BinPackingResult packItemsBFD(List<Integer> items, int binCapacity) {// 验证输入validateInput(items, binCapacity);// 排序物品List<Integer> sortedItems = new ArrayList<>(items);sortedItems.sort(Collections.reverseOrder());List<Bin> bins = new ArrayList<>();for (int item : sortedItems) {Bin bestBin = findBestBin(bins, item, binCapacity);if (bestBin != null) {bestBin.addItem(item);} else {Bin newBin = new Bin(binCapacity);newBin.addItem(item);bins.add(newBin);}}return new BinPackingResult(bins, binCapacity);}private static Bin findBestBin(List<Bin> bins, int item, int binCapacity) {Bin bestBin = null;int minRemaining = binCapacity + 1;for (Bin bin : bins) {if (bin.canAdd(item)) {int remaining = bin.getRemainingCapacity() - item;if (remaining < minRemaining) {bestBin = bin;minRemaining = remaining;}}}return bestBin;}private static void validateInput(List<Integer> items, int binCapacity) {if (binCapacity <= 0) {throw new IllegalArgumentException("箱子容量必须为正数");}for (int item : items) {if (item <= 0) {throw new IllegalArgumentException("物品大小必须为正数");}if (item > binCapacity) {throw new IllegalArgumentException("存在物品大小超过箱子容量");}}}
}
3.3 使用TreeSet优化查找
import java.util.*;public class BinPackingBFDWithTreeSet {public static void main(String[] args) {List<Integer> items = List.of(4, 8, 5, 1, 2, 3, 6, 7, 9, 4);int binCapacity = 10;BinPackingResult result = packItemsBFD(items, binCapacity);result.printBins();}static class Bin implements Comparable<Bin> {private final int capacity;private final List<Integer> items;private int currentWeight;public Bin(int capacity) {this.capacity = capacity;this.items = new ArrayList<>();this.currentWeight = 0;}public boolean canAdd(int item) {return currentWeight + item <= capacity;}public void addItem(int item) {if (!canAdd(item)) {throw new IllegalStateException("超出箱子容量");}items.add(item);currentWeight += item;}public int getRemainingCapacity() {return capacity - currentWeight;}public List<Integer> getItems() {return Collections.unmodifiableList(items);}@Overridepublic int compareTo(Bin other) {// 按剩余容量升序排列return Integer.compare(this.getRemainingCapacity(), other.getRemainingCapacity());}}static class BinPackingResult {private final List<Bin> bins;public BinPackingResult(List<Bin> bins) {this.bins = bins;}public void printBins() {System.out.println("使用的箱子数量: " + bins.size());for (int i = 0; i < bins.size(); i++) {Bin bin = bins.get(i);System.out.printf("箱子 %2d: %s (总大小: %2d)%n",i+1, bin.getItems(), bin.currentWeight);}}}public static BinPackingResult packItemsBFD(List<Integer> items, int binCapacity) {// 排序物品List<Integer> sortedItems = new ArrayList<>(items);sortedItems.sort(Collections.reverseOrder());List<Bin> bins = new ArrayList<>();TreeSet<Bin> binTree = new TreeSet<>();for (int item : sortedItems) {// 创建一个临时bin用于查找Bin tempBin = new Bin(binCapacity);tempBin.addItem(binCapacity - item); // 剩余容量=item的箱子// 找到剩余容量 >= item的最小箱子Bin candidate = binTree.ceiling(tempBin);if (candidate != null && candidate.canAdd(item)) {// 从TreeSet中移除,修改后再添加回去binTree.remove(candidate);candidate.addItem(item);binTree.add(candidate);} else {Bin newBin = new Bin(binCapacity);newBin.addItem(item);bins.add(newBin);binTree.add(newBin);}}return new BinPackingResult(bins);}
}
4. 算法分析与性能优化
4.1 时间复杂度分析
- 排序阶段:O(n log n)
- 装箱阶段:
- 基础实现:O(n²) - 每个物品遍历所有箱子
- TreeSet优化:O(n log n) - 每次查找O(log n)
4.2 空间复杂度
- O(n) - 需要存储所有物品和箱子信息
4.3 性能对比测试
import java.util.*;
import java.util.stream.IntStream;public class BFDPerformanceTest {public static void main(String[] args) {int numItems = 100000;int binCapacity = 100;List<Integer> items = generateRandomItems(numItems, binCapacity);// 预热BinPackingBFD.bestFitDecreasing(items.subList(0, 1000), binCapacity);BinPackingBFDAdvanced.packItemsBFD(items.subList(0, 1000), binCapacity);// 测试基础实现long start = System.currentTimeMillis();List<List<Integer>> bins1 = BinPackingBFD.bestFitDecreasing(items, binCapacity);long end = System.currentTimeMillis();System.out.printf("基础BFD实现: %5dms, 箱子数: %d%n", end-start, bins1.size());// 测试高级实现start = System.currentTimeMillis();BinPackingBFDAdvanced.BinPackingResult result = BinPackingBFDAdvanced.packItemsBFD(items, binCapacity);end = System.currentTimeMillis();System.out.printf("高级BFD实现: %5dms, 箱子数: %d, 平均填充率: %.2f%%%n", end-start, result.bins.size(), result.getAverageFillRate()*100);}private static List<Integer> generateRandomItems(int count, int maxSize) {Random random = new Random();return IntStream.range(0, count).map(i -> random.nextInt(maxSize) + 1).boxed().toList();}
}
5. 应用场景与扩展
5.1 实际应用案例
-
物流运输:
- 集装箱装载优化
- 卡车货物配载
- 航空货运管理
-
云计算:
- 虚拟机分配
- 容器调度
- 资源分配
-
生产制造:
- 原材料切割
- 生产任务调度
- 仓库货架管理
5.2 算法扩展变种
-
多维BFD:
- 考虑物品的多个维度(长、宽、高)
- 实现方式:扩展Bin类,添加多维容量检查
-
动态BFD:
- 处理动态到达的物品流
- 实现方式:结合在线算法策略
-
成本感知BFD:
- 不同箱子有不同的使用成本
- 实现方式:在选择箱子时考虑成本因素
-
带约束的BFD:
- 某些物品不能放在一起
- 实现方式:添加冲突检查逻辑
6. 与其他算法对比
6.1 BFD vs FFD
| 特性 | BFD | FFD |
|---|---|---|
| 选择策略 | 剩余空间最小的合适箱子 | 第一个能装下的箱子 |
| 空间利用率 | 通常更高 | 略低 |
| 时间复杂度 | O(n²)或O(n log n) | O(n²)或O(n log n) |
| 实现复杂度 | 稍复杂 | 较简单 |
| 适用场景 | 对空间利用率要求高的场景 | 一般场景 |
6.2 BFD与其他算法对比
-
Next Fit (NF):
- 只检查当前箱子,无法回溯
- 效率低但实现简单
-
First Fit (FF):
- 选择第一个能装下的箱子
- 比BFD快但空间利用率低
-
Worst Fit (WF):
- 选择剩余空间最大的箱子
- 适合希望均匀分布负载的场景
7. 完整Java实现(综合版)
import java.util.*;
import java.util.stream.Collectors;/*** 完整的BFD算法实现,包含所有优化和功能*/
public class ComprehensiveBFD {public static void main(String[] args) {// 示例使用List<Integer> items = generateItems(20, 10);int binCapacity = 10;System.out.println("物品列表: " + items);BFDResult result = pack(items, binCapacity);result.printAnalysis();}/*** BFD装箱结果类*/public static class BFDResult {private final List<Bin> bins;private final int binCapacity;private final long packingTime;public BFDResult(List<Bin> bins, int binCapacity, long packingTime) {this.bins = bins;this.binCapacity = binCapacity;this.packingTime = packingTime;}public int getBinCount() {return bins.size();}public double getAverageFillRate() {return bins.stream().mapToDouble(bin -> (double)bin.getUsedCapacity() / binCapacity).average().orElse(0);}public double getEfficiency() {int totalItems = bins.stream().mapToInt(bin -> bin.getItems().size()).sum();return (double)totalItems / (bins.size() * binCapacity);}public void printAnalysis() {System.out.println("\n装箱分析结果:");System.out.printf("箱子数量: %d\n", getBinCount());System.out.printf("平均填充率: %.2f%%\n", getAverageFillRate() * 100);System.out.printf("算法效率: %.4f\n", getEfficiency());System.out.printf("计算时间: %dms\n", packingTime);System.out.println("\n箱子详情:");bins.forEach(bin -> {System.out.printf("箱子 %2d: %s (使用率: %5.2f%%)%n",bins.indexOf(bin)+1, bin.getItems().stream().map(String::valueOf).collect(Collectors.joining(", ", "[", "]")),(double)bin.getUsedCapacity() / binCapacity * 100);});}}/*** 箱子类*/public static class Bin {private final List<Integer> items;private int usedCapacity;public Bin() {this.items = new ArrayList<>();this.usedCapacity = 0;}public boolean canAdd(int item, int binCapacity) {return usedCapacity + item <= binCapacity;}public void addItem(int item) {items.add(item);usedCapacity += item;}public List<Integer> getItems() {return Collections.unmodifiableList(items);}public int getUsedCapacity() {return usedCapacity;}}/*** 装箱方法*/public static BFDResult pack(List<Integer> items, int binCapacity) {long startTime = System.currentTimeMillis();// 验证输入validateInput(items, binCapacity);// 排序物品(降序)List<Integer> sortedItems = new ArrayList<>(items);sortedItems.sort(Collections.reverseOrder());List<Bin> bins = new ArrayList<>();// 使用TreeMap优化查找: key=剩余容量, value=箱子索引列表TreeMap<Integer, List<Integer>> remainingMap = new TreeMap<>();for (int item : sortedItems) {// 查找最小剩余容量 >= item的箱子Map.Entry<Integer, List<Integer>> entry = remainingMap.ceilingEntry(item);if (entry != null) {// 获取第一个匹配的箱子int binIndex = entry.getValue().get(0);Bin bin = bins.get(binIndex);// 更新TreeMapupdateTreeMap(remainingMap, bin, binIndex, item, binCapacity);// 添加物品到箱子bin.addItem(item);} else {// 创建新箱子Bin newBin = new Bin();newBin.addItem(item);bins.add(newBin);// 计算并添加剩余容量到TreeMapint remaining = binCapacity - item;if (remaining > 0) {remainingMap.computeIfAbsent(remaining, k -> new ArrayList<>()).add(bins.size() - 1);}}}long endTime = System.currentTimeMillis();return new BFDResult(bins, binCapacity, endTime - startTime);}private static void updateTreeMap(TreeMap<Integer, List<Integer>> map, Bin bin, int binIndex, int item, int binCapacity) {// 移除旧的剩余容量记录int oldRemaining = binCapacity - (bin.getUsedCapacity() - item);List<Integer> indices = map.get(oldRemaining);if (indices != null) {indices.remove(Integer.valueOf(binIndex));if (indices.isEmpty()) {map.remove(oldRemaining);}}// 添加新的剩余容量记录int newRemaining = binCapacity - bin.getUsedCapacity();if (newRemaining > 0) {map.computeIfAbsent(newRemaining, k -> new ArrayList<>()).add(binIndex);}}private static void validateInput(List<Integer> items, int binCapacity) {if (binCapacity <= 0) {throw new IllegalArgumentException("箱子容量必须为正数");}for (int item : items) {if (item <= 0) {throw new IllegalArgumentException("物品大小必须为正数");}if (item > binCapacity) {throw new IllegalArgumentException("存在物品大小超过箱子容量");}}}private static List<Integer> generateItems(int count, int maxSize) {return new Random().ints(count, 1, maxSize + 1).boxed().collect(Collectors.toList());}
}
8. 总结
最佳适应递减算法(BFD)是解决装箱问题的高效算法:
- 排序+贪心:通过先排序再贪心选择,实现高效装箱
- 空间利用率高:通常比FFD获得更好的装箱结果
- 灵活可扩展:可适应多种变种问题
- 平衡效率:在时间复杂度和空间利用率间取得良好平衡
在实际应用中,BFD算法特别适合:
- 对空间利用率要求高的场景
- 物品大小差异较大的情况
- 需要高质量近似解的场合
通过Java实现时,使用TreeSet/TreeMap等数据结构可以显著提高算法效率,特别是在处理大规模数据时。
更多资源:
https://www.kdocs.cn/l/cvk0eoGYucWA
本文发表于【纪元A梦】!
相关文章:

贪心算法应用:装箱问题(BFD算法)详解
贪心算法应用:装箱问题(BFD算法)详解 1. 装箱问题与BFD算法概述 1.1 装箱问题定义 装箱问题(Bin Packing Problem)是组合优化中的经典问题,其定义为: 给定n个物品,每个物品有大小wᵢ (0 < wᵢ ≤ C)无限数量的箱子…...

C#学习第27天:时间和日期的处理
时间和日期的核心概念 1. UTC 和 本地时间 UTC(Coordinated Universal Time): 是一种不受时区影响的世界标准时间。在网络通信和全球协作中,用于统一时间度量 本地时间(Local Time): 是根据所…...

编程技能:格式化打印05,格式控制符
专栏导航 本节文章分别属于《Win32 学习笔记》和《MFC 学习笔记》两个专栏,故划分为两个专栏导航。读者可以自行选择前往哪个专栏。 (一)WIn32 专栏导航 上一篇:编程技能:格式化打印04,sprintf 回到目录…...

MPLAB X IDE 软件安装与卸载
1、下载MPLAB X IDE V6.25 MPLAB X IDE | Microchip Technology 正常选Windows,点击Download,等待自动下载完成; MPLAB X IDE 一台电脑上可以安装多个版本; 2、安装MPLAB X IDE V6.25 右键以管理员运行;next; 勾选 I a…...

windows编程实现文件拷贝
项目源码链接: 实现文件拷贝功能(限制5GB大小) 81c57de 周不才/cpp_linux study - Gitee.com 知识准备: 1.句柄 句柄是一个用于标识和引用系统资源(如文件、窗口、进程、线程、位图等)的值。它不是资…...
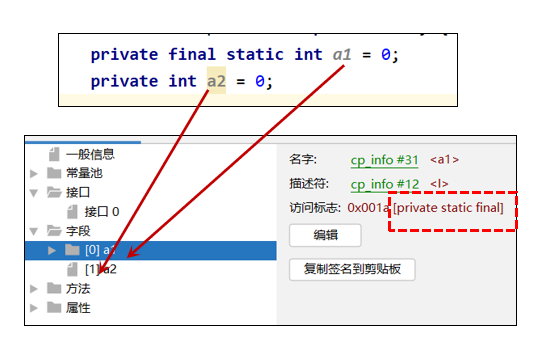
[6-01-01].第12节:字节码文件内容 - 属性表集合
JVM学习大纲 二、属性表集合: 2.1.属性计数器: 2.2.属性表: 2.3.字节码文件组成5 -> 属性: 1.属性主要指的是类的属性,比如源码的文件名、内部类的列表等 2.4.字节码文件组成3 -> 字段: 1.字段中…...

基于机器学习的水量智能调度研究
摘要:随着城市化进程的加速和水资源供需矛盾的日益突出,传统的水量调度模式因缺乏精准预测和动态调控能力,难以满足现代供水系统对高效性、稳定性和节能性的要求。本文针对供水系统中用水峰谷预测不准确、能耗高、供需失衡等核心问题…...

深度解码:我如何用“结构进化型交互学习方法”与AI共舞,从学习小白到构建复杂认知体系
嗨,亲爱的学习者们,思考者们,以及所有渴望在知识海洋中自由翱行却时常感到迷茫的朋友们: 你是否也曾有过这样的深夜,面对堆积如山的学习资料,眼神迷离,内心却一片荒芜?明明每个字都…...

深入浅出 Scrapy:打造高效、强大的 Python 网络爬虫
在数据为王的时代,高效获取网络信息是开发者必备的技能。今天我将为大家介绍 Python 爬虫领域的王者框架——Scrapy。无论你是数据工程师、分析师还是开发者,掌握 Scrapy 都能让你的数据采集效率提升数倍! 项目地址:https://github.com/scrapy/scrapy 官方文档:https://do…...

ES6 Promise 状态机
状态机:抽象的计算模型,根据特定的条件或者信号切换不同的状态 一、Promise 是什么? 简单来说,Promise 就是一个“承诺对象”。在ES6 里,有些代码执行起来需要点时间,比如加载文件、等待网络请求或者设置…...

Axure 与 Cursor 集成实现方案
Axure 与 Cursor 集成实现方案 以下是一个完整的 Axure 与 Cursor AI 集成的原型实现方案,通过自定义 JavaScript 代码实现无缝对接: 一、整体架构设计 #mermaid-svg-f9hQDSN4hijU3mJY {font-family:"trebuchet ms",verdana,arial,sans-seri…...

汽车加气站操作工证考试重点
汽车加气站操作工证考试重点 一、汽车加气站操作工证考试主要内容 汽车加气站操作工证是从事CNG(压缩天然气)和LNG(液化天然气)加气站作业人员的必备资格证书。随着新能源汽车的快速发展,该证书的市场需求持续增长&a…...

贪心算法应用:带权任务间隔调度问题详解
贪心算法应用:带权任务间隔调度问题详解 贪心算法是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是全局最好或最优的算法。带权任务间隔调度问题是贪心算法的一个经典应用场景。 问题定义…...

用电脑控制keysight示波器
KEYSIGHT示波器HD304MSO性能 亮点: 体验 200 MHz 至 1 GHz 的带宽和 4 个模拟通道。与 12 位 ADC 相比,使用 14 位模数转换器 (ADC) 将垂直分辨率提高四倍。使用 10.1 英寸电容式触摸屏轻松查看和分析您的信号。捕获 50 μVRMS …...

LLaMA-Factory - 批量推理(inference)的脚本
scripts/vllm_infer.py 是 LLaMA-Factory 团队用于批量推理(inference)的脚本,基于 vLLM 引擎,支持高效的并行推理。它可以对一个数据集批量生成模型输出,并保存为 JSONL 文件,适合大规模评测和自动化测试。…...

React从基础入门到高级实战:React 高级主题 - 测试进阶:从单元测试到端到端测试的全面指南
React 测试进阶:从单元测试到端到端测试的全面指南 引言 在2025年的React开发环境中,测试不仅是代码质量的保障,更是提升开发效率和用户体验的关键支柱。随着React应用的复杂性不断增加,高级测试技术——如端到端(E2…...

Ansible 剧本精粹 - 编写你的第一个 Playbook
Ansible 剧本精粹 - 编写你的第一个 Playbook 如果说 Ansible Ad-Hoc 命令像是你对厨房里的助手发出的零散口头指令(“切个洋葱”、“烧开水”),那么 Playbook 就是一份完整、详细、写在纸上的菜谱。它列明了所有需要的“食材”(变量),详细的“烹饪步骤”(任务),甚至还…...

【Elasticsearch】Elasticsearch 核心技术(二):映射
Elasticsearch 核心技术(二):映射 1.什么是映射(Mapping)1.1 元字段(Meta-Fields)1.2 数据类型 vs 映射类型1.2.1 数据类型1.2.2 映射类型 2.实际运用案例案例 1:电商产品索引映射案…...

【计算机网络】网络层协议
1. ICMP协议的介绍及应用 IP协议的助手 —— ICMP 协议 ping 是基于 ICMP 协议工作的,所以要明白 ping 的工作,首先我们先来熟悉 ICMP 协议。 ICMP 全称是 Internet Control Message Protocol,也就是互联网控制报文协议。 里面有个关键词 …...

.NET Core接口IServiceProvider
.NET Core 接口 IServiceProvider 深度剖析 在 .NET Core 和 .NET 5 的世界里,依赖注入(Dependency Injection,简称 DI)是构建可维护、可测试应用程序的关键技术。而 IServiceProvider 接口,正是依赖注入机制中的核心…...

结构型设计模式之Proxy(代理)
结构型设计模式之Proxy(代理) 前言: 代理模式,aop环绕通知,动态代理,静态代理 都是代理的一种,这次主要是记录设计模式的代理demo案例,详情请看其他笔记。 1)意图 为其…...

案例分享--汽车制动卡钳DIC测量
制动系统是汽车的主要组成部分,是汽车的主要安全部件之一。随着车辆性能的不断提高,车速不断提升,对车辆的制动系统也随之提出了更高要求,因此了解车辆制动系统中每个部件的动态行为成为了制动系统优化的主要途径,同时…...

Redis Set集合命令、内部编码及应用场景(详细)
文章目录 前言普通命令SADDSMEMBERSSISMEMBERSCARDSPOPSMOVESREM 集合间操作SINTERSINTERSTORESUNIONSUNIONSTORESDIFFSDIFFSTORE 命令小结内部编码使用场景 前言 集合类型也是保存多个字符串类型的元素的,但和列表类型不同的是,集合中 1)元…...

C++算法动态规划1
DP定义: 动态规划是分治思想的延申,通俗一点来说就是大事化小,小事化无的艺术。 在将大问题化解为小问题的分治过程中,保存对这些小问题已经处理好的结果,并供后面处理更大规模的问题时直接使用这些结果。 动态规划具…...

【快速预览经典深度学习模型:CNN、RNN、LSTM、Transformer、ViT全解析!】
🚀快速预览经典深度学习模型:CNN、RNN、LSTM、Transformer、ViT全解析! 📌你是否还在被深度学习模型名词搞混?本文带你用最短时间掌握五大经典模型的核心概念和应用场景,助你打通NLP与CV的任督二脉…...

KaiwuDB在边缘计算领域的应用与优势
KaiwuDB 在边缘计算场景中主要应用于 工业物联网(IIoT)、智能电网、车联网 等领域,通过其分布式多模架构和轻量化设计,在边缘侧承担 数据实时处理、本地存储与协同分析 的核心作用。以下是具体案例和功能解析: 1. 典型…...

如何避免二极管过载?
如何避免二极管过载? 二极管作为电路中的基础元件,其过载可能导致性能下降甚至烧毁。以下从选型、安装、保护设计及散热四方面提供实用解决二极管过载方案: 精准选型匹配需求 根据电路特性选择二极管类型:高频电路优先选用肖特基…...

Vue.js组件开发系统性指南
结合核心概念、最佳实践及性能优化策略,帮助您构建高效可维护的组件体系: 一、组件基础与核心结构 1.单文件组件(SFC)组织 模板:使用<template>定义HTML结构,遵循单根元素原则。 逻辑:在<script>中通过export default导出组件选项(数据、方法、生命周期钩…...

React---day9
11、css 11.1 styled的基本使用 CSS-in-JS的模式就是一种将样式(CSS)也写入到JavaScript中的方式,并且可以方便的使用JavaScript的状态; npm add styled-componentsconst Title styled.h1font-size: 1.5em;text-align: center…...

设计模式 - 模板方法模式
该模式将定义一个操作中的算法骨架,并将算法的一些步骤延迟到子类中实现,使得子类可以在不改变算法结构的情况下重定义算法的某些特定步骤。 例如,炒菜的步骤是固定的,具体可分为倒油、热油、倒蔬菜、倒调料品、翻炒等。通过模板…...
