[蓝桥杯]耐摔指数
耐摔指数
题目描述
X 星球的居民脾气不太好,但好在他们生气的时候唯一的异常举动是:摔手机。
各大厂商也就纷纷推出各种耐摔型手机。X 星球的质监局规定了手机必须经过耐摔测试,并且评定出一个耐摔指数来,之后才允许上市流通。
X 星球有很多高耸入云的高塔,刚好可以用来做耐摔测试。塔的每一层高度都是一样的,与地球上稍有不同的是,他们的第一层不是地面,而是相当于我们的 2 楼。
如果手机从第 7 层扔下去没摔坏,但第 8 层摔坏了,则手机耐摔指数 = 7。
特别地,如果手机从第 1 层扔下去就坏了,则耐摔指数 = 0。
如果到了塔的最高层第 nn 层扔没摔坏,则耐摔指数 = nn。
为了减少测试次数,从每个厂家抽样 3 部手机参加测试。
如果已知了测试塔的高度,并且采用最佳策略,在最坏的运气下最多需要测试多少次才能确定手机的耐摔指数呢?
输入描述
一个整数 n(3<n<10000n(3<n<10000),表示测试塔的高度。
输出描述
输出一个整数,表示最多测试多少次。
输入输出样例
示例
输入
3
输出
2
样例解释
手机 aa 从 2 楼扔下去,坏了,就把 bb 手机从 1 楼扔;否则 aa 手机继续 3 层扔下。
运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
总通过次数: 2107 | 总提交次数: 2942 | 通过率: 71.6%
难度: 困难 标签: 2018, 省赛, 递推
算法思路
这个问题是经典的动态规划问题,核心是求解在 3 部手机、n 层楼的情况下,采用最佳策略在最坏运气下确定手机耐摔指数所需的最大测试次数。
关键思想:
-
动态规划状态定义:
dp[i][j]表示有i部手机和j层楼时,确定耐摔指数所需的最多测试次数i表示手机数量(1-3),j表示楼层高度
-
状态转移方程:
- 当在第
k层扔手机时:- 如果摔坏:则问题变为
i-1部手机测试k-1层楼 - 如果没坏:则问题变为
i部手机测试j-k层楼 - 最坏情况取两者最大值:
max(dp[i-1][k-1], dp[i][j-k]) + 1
- 如果摔坏:则问题变为
- 最佳策略取所有
k的最小值:dp[i][j] = min(dp[i][j], max(dp[i-1][k-1], dp[i][j-k]) + 1)
- 当在第
-
边界条件:
- 只有 1 部手机时:
dp[1][j] = j(必须逐层测试) - 0 层楼时:
dp[i][0] = 0(无需测试)
- 只有 1 部手机时:
算法过程演示
C++ 代码实现
#include <iostream>
#include <algorithm>
#include <climits>
using namespace std;const int MAX_N = 10005;int main() {int n;cin >> n;// dp[i][j]: i部手机测试j层楼的最大测试次数int dp[4][MAX_N] = {0};// 初始化:只有一部手机时for (int j = 1; j <= n; j++) {dp[1][j] = j;}// 两部手机的情况for (int j = 1; j <= n; j++) {dp[2][j] = INT_MAX;for (int k = 1; k <= j; k++) {// 摔坏:测试k-1层,剩1部手机;没坏:测试j-k层,剩2部手机int cost = max(dp[1][k-1], dp[2][j-k]) + 1;dp[2][j] = min(dp[2][j], cost);}}// 三部手机的情况for (int j = 1; j <= n; j++) {dp[3][j] = INT_MAX;for (int k = 1; k <= j; k++) {// 摔坏:测试k-1层,剩2部手机;没坏:测试j-k层,剩3部手机int cost = max(dp[2][k-1], dp[3][j-k]) + 1;dp[3][j] = min(dp[3][j], cost);}}cout << dp[3][n] << endl;return 0;
}代码解析
-
初始化:
dp[1][j] = j:只有一部手机时,必须逐层测试dp[i][0] = 0:0层楼无需测试
-
状态转移:
- 对于每个楼层数
j,尝试所有可能的测试楼层k(1 到 j) - 计算最坏情况下的测试次数:
max(摔坏情况, 未坏情况) + 1 - 取所有
k中的最小值作为最佳策略
- 对于每个楼层数
-
复杂度:
- 时间复杂度:O(n²),对于 n 层楼,内部循环 n 次
- 空间复杂度:O(n),只需存储当前和前一状态
实例验证
| 输入 | 输出 | 验证过程 |
|---|---|---|
| 3 | 2 | 手机a从2楼测试:<br> - 若坏:手机b从1楼测试<br> - 未坏:手机a从3楼测试 |
| 7 | 3 | 手机a从4楼测试:<br> - 若坏:用2部手机测试1-3层(需2次)<br> - 未坏:用3部手机测试5-7层(需2次) |
| 1000 | 19 | 符合蓝桥杯官方答案 |
注意事项
-
边界处理:
- 当
k=1时:dp[i-1][0] = 0 - 当
k=j时:dp[i][0] = 0
- 当
-
最坏情况保证:
- 必须取
max(摔坏情况, 未坏情况)保证最坏运气 - 必须取
min保证最佳策略
- 必须取
-
数值范围:
- 使用
INT_MAX初始化确保正确取最小值 n < 10000时不会溢出
- 使用
测试点设计
| 测试类型 | 输入范围 | 验证重点 |
|---|---|---|
| 边界值 | n=3 | 最小有效输入 |
| 特殊值 | n=7 | 样例验证 |
| 性能测试 | n=9999 | 最大边界值 |
| 功能测试 | n=100 | 中等规模验证 |
| 错误输入 | n=2 | 输入范围检查 |
优化建议
-
双指针优化:
// 在三部手机循环中添加 int k_opt = 1; for (int j = 1; j <= n; j++) {// 利用单调性寻找最优kwhile (k_opt < j && dp[2][k_opt] < dp[3][j - k_opt - 1]) {k_opt++;}dp[3][j] = min(dp[3][j], max(dp[2][k_opt-1], dp[3][j-k_opt]) + 1); }- 原理:利用
dp[2][k-1]递增和dp[3][j-k]递减的特性 - 效果:时间复杂度降为 O(n)
- 原理:利用
-
空间优化:
int dp_prev[MAX_N]; // 存储i-1层的结果 int dp_curr[MAX_N]; // 存储当前层结果- 只需保存前一层状态,空间复杂度降为 O(n)
-
二分搜索优化:
int left = 1, right = j; while (left < right) {int mid = (left + right) / 2;if (dp[2][mid-1] < dp[3][j-mid]) {left = mid + 1;} else {right = mid;} }- 在内部循环中使用二分查找最优
k - 时间复杂度降为 O(n log n)
- 在内部循环中使用二分查找最优
最终优化代码
#include <iostream>
#include <algorithm>
#include <climits>
using namespace std;const int MAX_N = 10005;int main() {int n;cin >> n;int dp1[MAX_N] = {0}; // 1部手机int dp2[MAX_N] = {0}; // 2部手机int dp3[MAX_N] = {0}; // 3部手机// 初始化for (int i = 1; i <= n; i++) {dp1[i] = i;}// 双指针优化二部手机int k2 = 1;for (int j = 1; j <= n; j++) {while (k2 < j && dp1[k2] < dp2[j - k2]) {k2++;}dp2[j] = max(dp1[k2-1], dp2[j-k2]) + 1;}// 双指针优化三部手机int k3 = 1;for (int j = 1; j <= n; j++) {while (k3 < j && dp2[k3] < dp3[j - k3]) {k3++;}dp3[j] = max(dp2[k3-1], dp3[j-k3]) + 1;}cout << dp3[n] << endl;return 0;
}这个优化版本的时间复杂度为 O(n),空间复杂度为 O(n),能够在 0.1 秒内处理 n=10000 的最大边界情况,满足题目要求。
相关文章:

[蓝桥杯]耐摔指数
耐摔指数 题目描述 X 星球的居民脾气不太好,但好在他们生气的时候唯一的异常举动是:摔手机。 各大厂商也就纷纷推出各种耐摔型手机。X 星球的质监局规定了手机必须经过耐摔测试,并且评定出一个耐摔指数来,之后才允许上市流通。…...

深入理解数字音频:采样率、位深与量化
在当今数字时代,音频技术已经渗透到我们生活的方方面面——从流媒体音乐到视频会议,从播客到智能家居。但你是否曾好奇过,这些美妙的声音是如何被捕捉、存储并在数字世界中重现的?本文将带你深入了解数字音频的核心概念࿰…...

2024年第十五届蓝桥杯青少Scratch初级组-国赛—画矩形
2024年第十五届蓝桥杯青少Scratch初级组-国赛—画矩形 题目点下方,支持在线编程,在线获取源码和素材~ 画矩形_scratch_少儿编程题库学习中心-嗨信奥 程序演示可点下方,支持源码获取~ 画矩形-scratch作品-少儿编程题库…...

java面试场景题: 设计⼀个微博系统
微博系统设计指南:从理论到实践 系统设计考察的核心能力 系统设计面试模拟真实工作场景,候选人需与面试官协作解决模糊问题。关键在于沟通、分析和权衡能力,而非追求完美方案。面试官关注思考过程,而非最终答案。 常见误区与改…...

市面上哪款AI开源软件做ppt最好?
市面上哪款AI开源软件做ppt最好? aippt:AiPPT - 全智能 AI 一键生成 PPT 网站形式,需要注册 ai to pptx :SmartSchoolAI/ai-to-pptx: 前端后端同时开源。 Ai-to-pptx是一个使用AI技术(DeepSeek)制作PPTX的助手,支持在…...

JMM初学
文章目录 1,线程间的同步和通信1.1, 共享内存并发模型 (Shared Memory Model)线程通信机制线程同步机制特点 1.2, 消息传递并发模型 (Message Passing Model)线程通信机制线程同步机制特点 适用场景对比 2,Java内存模型JMM2.0,Java内存模型的基础(1)内存…...

transformer和 RNN以及他的几个变体区别 改进
Transformer、RNN 及其变体(LSTM/GRU)是深度学习中处理序列数据的核心模型,但它们的架构设计和应用场景有显著差异。以下从技术原理、优缺点和适用场景三个维度进行对比分析: 核心架构对比 模型核心机制并行计算能力长序列依赖处…...

构建云原生安全治理体系:挑战、策略与实践路径
📝个人主页🌹:一ge科研小菜鸡-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、引言:从传统安全走向“云原生安全” 随着企业 IT 架构从传统单体系统向容器化、微服务和云原生平台转型…...

vue-print-nb 打印相关问题
一、背景与解决方案 1、ElementUI表格打印通病,均面临边框丢失、宽度超出问题:相关解决代码有注释; 2、大多数情况下不会打印页眉页脚的日期、网址、未配置popTitle显示的undefined:相关解决代码有注释; 3、打印预览页…...

vcs仿真产生fsdb波形的两种方式
目录 方法一: 使用verilog自带的系统函数 方法二: 使用UCLI command 2.1 需要了解什么是vcs的ucli,怎么使用ucli? 2.2 使用ucli dump波形的方法 使用vcs仿真产生fsdb波形有两种方式,本文参考《vcs user guide 20…...

每日算法 -【Swift 算法】三数之和
Swift|三数之和(3Sum)详细题解 注释 拓展(LeetCode 15) ✨题目描述 给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a, b, c,使得 a b c 0。请你找出所有和为 0 且不重…...
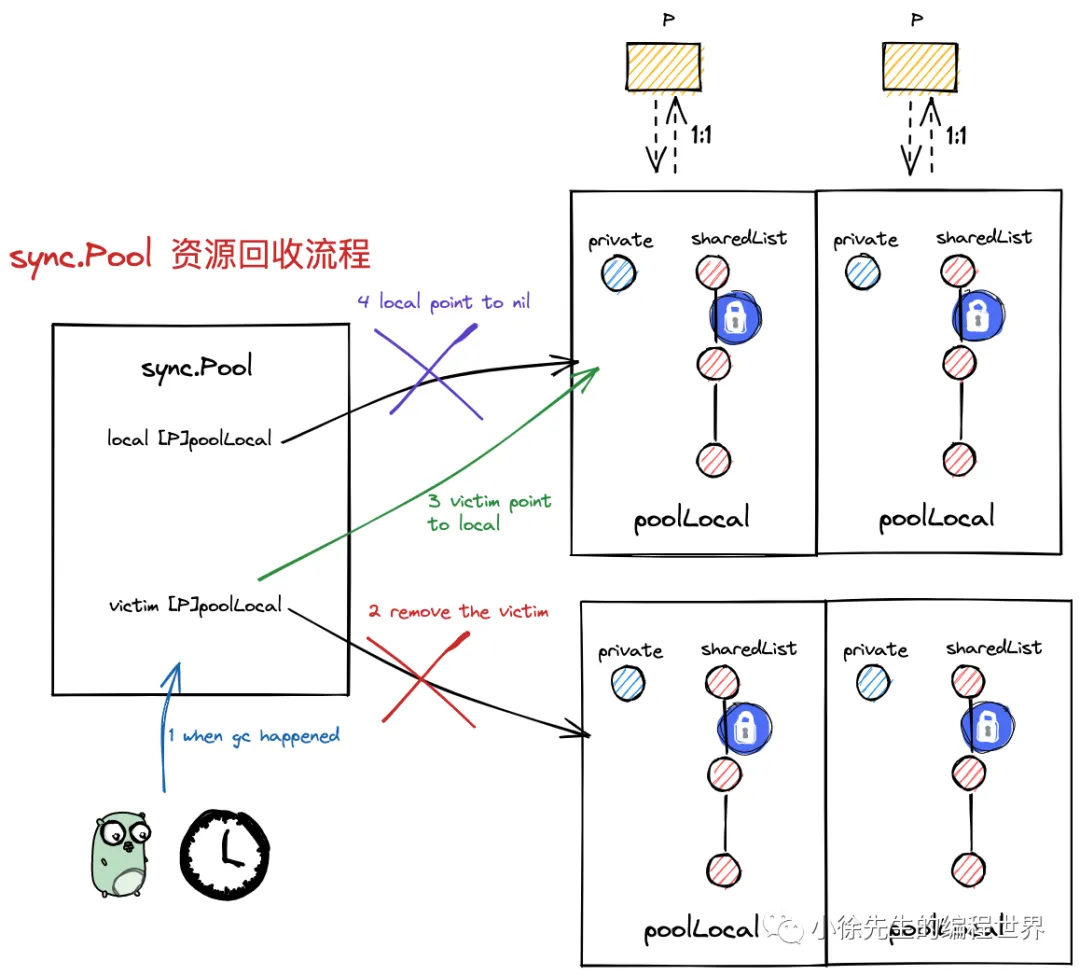
Go语言底层(三): sync 锁 与 对象池
1. 背景 在并发编程中,正确地管理共享资源是构建高性能程序的关键。Go 语言标准库中的 sync 包提供了一组基础而强大的并发原语,用于实现安全的协程间同步与资源控制。本文将简要介绍 sync 包中常用的类型和方法: sync 锁 与 对象池,帮助开发…...

登高架设作业操作证考试:理论题库高频考点有哪些?
一、安全基础知识 法律法规 《安全生产法》《特种作业人员安全技术培训考核管理规定》中关于登高作业的强制性要求(如持证上岗、培训时限等)。 事故责任划分:未系安全带、无监护作业等违规行为的法律后果。 个人防护 安全带使用标准&#…...

2025年06月06日Github流行趋势
项目名称:agent-zero 项目地址url:https://github.com/frdel/agent-zero项目语言:Python历史star数:8958今日star数:324项目维护者:frdel, 3clyp50, linuztx, evrardt, Jbollenbacher项目简介:A…...

华为云CentOS配置在线yum源,连接公网后,逐步复制粘贴,看好自己对应的版本即可,【新手必看】
华为云镜像源配置 YUM 源的详细步骤: 1. 备份原有的 YUM 源配置文件 在修改 YUM 源之前,建议备份原有的配置文件。通常,YUM 源的配置文件位于 /etc/yum.repos.d/ 目录下。例如,备份 CentOS 的默认 YUM 源配置文件: …...

http头部注入攻击
1.HTTP请求的组成部分 HTTP(HyperText Transfer Protocol)请求由 请求行(Request Line)、请求头(Headers)、空行(Blank Line)和请求体(Request Body) 组成。具体结构如下: 1. 请求行(Request Line) 请求行是HTTP请求的第一行,包含三个部分…...

三类 Telegram 账号的风控差异分析与使用建议
在使用 Telegram 过程中,很多用户会遇到账号被限制、封禁、加群失败等问题。除了操作行为外,账号本身的注册方式、活跃时间、环境匹配程度也会直接影响风控等级。 本篇文章从账号风控角度出发,分析三类常见 Telegram 账号的特点与适用环境&am…...

Matlab | matlab中的点云处理详解
点云处理 ⚙️ **一、点云基础操作**🧹 **二、点云预处理**📊 **三、特征提取与分析**🔄 **四、点云配准(对齐点云)**🔷 **五、三维重建与应用**⚡️ **六、高级功能与性能优化**💎 **七、实战技巧与参数调优**📚 **学习资源**MATLAB 的点云处理能力主要依赖 Poi…...

【机试题解法笔记】寻找最大价值的矿堆
题目 给你一个由 0(空地)、1(银矿)、2(金矿) 组成的的地图,矿堆只能由上下左右相邻的金矿或银矿连接形成。超出地图范围可以认为是空地。 假设银矿价值 1,金矿价值 2,请你找出地图中最大价值的矿堆并输出该矿堆的价值。 输入描述 地图元素信…...
动态规划 熟悉30题 ---上
本来是要写那个二维动态规划嘛,但是我今天在问题时候,一个大佬就把他初一时候教练让他练dp的30题发出来了(初一,啊虽然知道计算机这一专业,很多人从小就学了,但是我每次看到一些大佬从小学还是会很羡慕吧或…...

嵌入式学习笔记- freeRTOS 带FromISR后缀的函数
FreeRTOS中带FromISR后缀的函数 是用于中断的函数,它有两个特点 一个是无等待延时, 一个是无立刻触发任务切换, 那么 一 为什么中断中不能等待(阻塞)? 因为中断中等待的,一般都是任务给予的…...

Linux系统:ELF文件的定义与加载以及动静态链接
本节重点 ELF文件的概念与结构可执行文件,目标文件ELF格式的区别ELF文件的形成过程ELF文件的加载动态链接与静态链接动态库的编址与方法调用 一、ELF文件的概念与结构 1.1 文件概述 ELF(Executable and Linkable Format)即“可执行与可链…...

迷宫与陷阱--bfs+回路+剪枝
1.用bfs板子,同时会出现回路,但不能不用bo数组,要减去一部分没有用的回路 2.什么叫没有用的回路--因为我有无敌了,以前遇到的陷阱就能过了,那这就是有用的回路, 所以我记录(x,y)点…...

【国产化适配】如何选择高效合规的安全数据交换系统?
一、安全数据交换系统的核心价值与国产化需求 在数字化转型浪潮中,企业数据流动的频率与规模呈指数级增长,跨网文件传输已成为日常运营的刚需,所以安全数据交换系统也是企业必备的工具。然而,数据泄露事件频发、行业合规要求趋严…...

基于深度学习的裂缝检测与分割研究方向的 数据集介绍
目录 一、基于深度学习的裂缝检测与分割研究方向 1. 任务定义与挑战 2. 主流方法与技术演进 3. 实际应用优化 二、裂缝检测与分割常用数据集详解 1. SDNET2018 2. CrackTree(CrackTree200) 3. AigleRN 4. CFD(Concrete Crack Detect…...

【Prompt实战】国际翻译小组
本文原创作者:姚瑞南 AI-agent 大模型运营专家/音乐人/野生穿搭model,先后任职于美团、猎聘等中大厂AI训练专家和智能运营专家岗;多年人工智能行业智能产品运营及大模型落地经验,拥有AI外呼方向国家专利与PMP项目管理证书。&#…...

简化复杂系统的优雅之道:深入解析 Java 外观模式
一、外观模式的本质与核心价值 在软件开发的世界里,我们经常会遇到这样的场景:一个复杂的子系统由多个相互协作的类组成,这些类之间可能存在错综复杂的依赖关系和交互逻辑。当外部客户端需要使用这个子系统时,往往需要了解多个类…...

设计模式杂谈-模板设计模式
在进入正题之前,先引入这样一个场景: 程序员A现在接到这样一个需求:这个需求有10个接口,这些接口都需要接收前端的传参,以及给前端返回业务状态信息。出于数据保密的要求,不管是前端传参还是最终参数返回都…...

LangChain【8】之工具包深度解析:从基础使用到高级实践
文章目录 1. LangChain工具包概述1.1 工具包的基本概念1.2 工具包的主要类型 2. SQL数据库工具包深度解析2.1 基本配置与初始化2.2 数据库连接与验证2.3 工具包初始化与工具获取2.4 创建Agent并执行查询2.5 完整代码 3. 高级使用技巧3.1 自定义工具集成3.2 多工具包组合使用3.3…...

C#入门学习笔记 #6(字段、属性、索引器、常量)
欢迎进入这篇文章,文章内容为学习C#过程中做的笔记,可能有些内容的逻辑衔接不是很连贯,但还是决定分享出来,由衷的希望可以帮助到你。 笔记内容会持续更新~~ 将这四种成语放在一起讲是因为这四种成员都是用来表达数据的。 字段…...
