当前位置：首页 > article >正文

【Python 算法零基础 4.排序 ⑨ 堆排序】

article 2025/6/7 18:38:09

目录

一、问题描述

二、算法对比

1.朴素算法

① 数组模拟容器

② 有序数组模拟容器

2.二叉堆

① 二叉堆特点

② 数组表示二叉树

③ 堆

④ 大顶堆

⑤ 小顶堆

⑥ 元素插入

⑦ 获取堆顶

⑧ 堆顶元素删除

三、代码分析

1.工具函数

2.调整大顶堆函数

Ⅰ、计算子节点索引

Ⅱ、找出最大值索引

Ⅲ、交换并递归调整

3.堆排序流程

Ⅰ、构建最大堆

Ⅱ、交换元素并调整堆

四、实战练习

912. 排序数组

思路与算法

关卡一一都击破

—— 25.5.30

选择排序回顾

① 遍历数组：从索引 0 到 n-1（n 为数组长度）。

② 每轮确定最小值：假设当前索引 i 为最小值索引 min_index。从 i+1 到 n-1 遍历，若找到更小元素，则更新 min_index。

③ 交换元素：若 min_index ≠ i，则交换 arr[i] 与 arr[min_index]。

'''
① 遍历数组：从索引 0 到 n-1（n 为数组长度）。② 每轮确定最小值：假设当前索引 i 为最小值索引 min_index。从 i+1 到 n-1 遍历，若找到更小元素，则更新 min_index。③ 交换元素：若 min_index ≠ i，则交换 arr[i] 与 arr[min_index]。
'''def selectionSort(arr: List[int]):n = len(arr)for i in range(n):min_index = ifor j in range(i+1, n):if arr[j] < arr[min_index]:min_index = jif min_index != i:arr[i], arr[min_index] = arr[min_index], arr[i]return arr

冒泡排序回顾

① 初始化：设数组长度为 n。

② 外层循环：遍历 i 从 0 到 n-1（共 n 轮）。

③ 内层循环：对于每轮 i，遍历 j 从 0 到 n-i-2。

④ 比较与交换：若 arr[j] > arr[j+1]，则交换两者。

⑤ 结束条件：重复步骤 2-4，直到所有轮次完成。

'''
① 初始化：设数组长度为 n。② 外层循环：遍历 i 从 0 到 n-1（共 n 轮）。③ 内层循环：对于每轮 i，遍历 j 从 0 到 n-i-1。④ 比较与交换：若 arr[j] > arr[j+1]，则交换两者。⑤ 结束条件：重复步骤 2-4，直到所有轮次完成。
'''
def bubbleSort(arr: List[int]):n = len(arr)for i in range(n):for j in range(n-i-1):if arr[j] > arr[j+1]:arr[j], arr[j+1] = arr[j+1], arr[j]return arr

插入排序回顾

① 遍历未排序元素：从索引 1 到 n-1。

② 保存当前元素：将 arr[i] 存入 current。

③ 元素后移：从已排序部分的末尾（索引 j = i-1）向前扫描，将比 current 大的元素后移。直到找到第一个不大于 current 的位置或扫描完所有元素。

④ 插入元素：将 current 放入 j+1 位置。

'''
① 遍历未排序元素：从索引 1 到 n-1。② 保存当前元素：将 arr[i] 存入 current。③ 元素后移：从已排序部分的末尾（索引 j = i-1）向前扫描，将比 current 大的元素后移。直到找到第一个不大于 current 的位置或扫描完所有元素。④ 插入元素：将 current 放入 j+1 位置。
'''
def insertSort(arr: List[int]):n = len(arr)for i in range(n):current = arr[i]j = i - 1while current < arr[j] and j >0:arr[j+1] = arr[j]j -= 1arr[j + 1] = currentreturn arr

计数排序回顾

① 初始化：设数组长度为 n，元素最大值为 r。创建长度为 r+1 的计数数组 count，初始值全为 0。

② 统计元素频率：遍历原数组 arr，对每个元素 x，将 count[x] 加 1。

③ 重构有序数组：初始化索引 index = 0。遍历计数数组 count，索引 v 从 0 到 r，若 count[v] > 0，则将 v 填入原数组 arr[index]，并将 index 加 1。count[v] - 1，重复此步骤直到 count[v] 为 0。

④ 结束条件：当计数数组遍历完成时，排序结束。

'''
输入全为非负整数，且所有元素 ≤ r① 初始化：设数组长度为 n，元素最大值为 r。创建长度为 r+1 的计数数组 count，初始值全为 0。② 统计元素频率：遍历原数组 arr，对每个元素 x，将 count[x] 加 1。③ 重构有序数组：初始化索引 index = 0。遍历计数数组 count，索引 v 从 0 到 r，
若 count[v] > 0，则将 v 填入原数组 arr[index]，并将 index 加 1。
count[v] - 1，重复此步骤直到 count[v] 为 0。④ 结束条件：当计数数组遍历完成时，排序结束。
'''def countingSort(arr: List[int], r: int):# count = [0] * len(r + 1)count = [0 for i in range(r + 1)]for x in arr:count[x] += 1index = 0for v in range(r + 1):while count[v] > 0:arr[index] = vindex += 1count[v] -= 1return arr

归并排序回顾

Ⅰ、递归分解列表

① 终止条件：若链表为空或只有一个节点（head is None 或 head.next is None），直接返回头节点。

② 快慢指针找中点：初始化 slow 和 fast 指针，slow 指向头节点，fast 指向头节点的下一个节点。fast 每次移动两步，slow 每次移动一步。当 fast 到达末尾时，slow 恰好指向链表的中间节点。

③ 分割链表：将链表从中点断开，head2 指向 slow.next（后半部分的头节点）。将 slow.next 置为 None，切断前半部分与后半部分的连接。

④ 递归排序子链表：对前半部分（head）和后半部分（head2）分别递归调用 mergesort 函数。

Ⅱ、合并两个有序列表

① 创建虚拟头节点：创建一个值为 -1 的虚拟节点 zero，用于简化边界处理。使用 current 指针指向 zero，用于构建合并后的链表。

② 比较并合并节点：遍历两个子链表 head1 和 head2，比较当前节点的值：若 head1.val <= head2.val，将 head1 接入合并链表，并移动 head1 指针。否则，将 head2 接入合并链表，并移动 head2 指针。每次接入节点后，移动 current 指针到新接入的节点。

③ 处理剩余节点：当其中一个子链表遍历完后，将另一个子链表的剩余部分直接接入合并链表的末尾。

④ 返回合并后的链表：虚拟节点 zero 的下一个节点即为合并后的有序链表的头节点。

'''
Ⅰ、递归分解列表① 终止条件：若链表为空或只有一个节点（head is None 或 head.next is None），直接返回头节点。② 快慢指针找中点：初始化 slow 和 fast 指针，slow 指向头节点，fast 指向头节点的下一个节点。fast 每次移动两步，slow 每次移动一步。当 fast 到达末尾时，slow 恰好指向链表的中间节点。③ 分割链表：将链表从中点断开，head2 指向 slow.next（后半部分的头节点）。将 slow.next 置为 None，切断前半部分与后半部分的连接。④ 递归排序子链表：对前半部分（head）和后半部分（head2）分别递归调用 mergesort 函数。Ⅱ、合并两个有序列表① 创建虚拟头节点：创建一个值为 -1 的虚拟节点 zero，用于简化边界处理。使用 current 指针指向 zero，用于构建合并后的链表。② 比较并合并节点：遍历两个子链表 head1 和 head2，比较当前节点的值：若 head1.val <= head2.val，将 head1 接入合并链表，并移动 head1 指针。否则，将 head2 接入合并链表，并移动 head2 指针。每次接入节点后，移动 current 指针到新接入的节点。③ 处理剩余节点：当其中一个子链表遍历完后，将另一个子链表的剩余部分直接接入合并链表的末尾。④ 返回合并后的链表：虚拟节点 zero 的下一个节点即为合并后的有序链表的头节点。
'''
def mergesort(self, head: ListNode):if head is None or head.next is None:return headslow, fast = head, head.nextwhile fast and fast.next:slow = slow.nextfast = fast.next.nexthead2 = slow.nextslow.next = Nonereturn self.merge(self.mergesort(head), self.mergesort(head2))def merge(self, head1: ListNode, head2: ListNode):zero = ListNode(-1)current = zerowhile head1 and head2:if head1.val <= head2.val:current.next = head1head1 = head1.nextelse:current.next = head2head2 = head2.nextcurrent = current.nextcurrent.next = head1 if head1 else head2return zero.next

快速排序回顾

Ⅰ、分区函数 Partition

① 随机选择基准元素：根据左右边界下标随机选择基准元素（选择的是元素并非下标），将基准元素赋值变量进行后续比较

② 交换基准元素：将基准元素移动到最左边，将基准元素存储在变量中，

③ 分区操作：对于基准元素右边的元素，找到第一个小于基准元素的值，移动到最左边；对于基准元素左边的元素，找到第一个大于基准元素的值，移动到最右边

④ 返回基准元素的最终位置：循环执行完毕后，基准元素左边的值都小于它，基准元素右边的值都大于它

Ⅱ、递归快速排序函数

① 定义递归终止条件：当左索引小于右索引时，结束递归

② 分区操作： 执行第一次分区操作，找到基准元素

③ 递归调用分区函数：将基准元素的左边、右边部分分别传入递归函数进行排序

'''
Ⅰ、分区函数 Partition① 随机选择基准元素：根据左右边界下标随机选择基准元素（选择的是元素并非下标），将基准元素赋值变量进行后续比较② 交换基准元素：将基准元素移动到最左边，将基准元素存储在变量中，③ 分区操作：对于基准元素右边的元素，找到第一个小于基准元素的值，移动到最左边；对于基准元素左边的元素，找到第一个大于基准元素的值，移动到最右边④ 返回基准元素的最终位置：循环执行完毕后，基准元素左边的值都小于它，基准元素右边的值都大于它Ⅱ、递归排序函数① 定义递归终止条件：当左索引小于右索引时，结束递归② 分区操作： 执行第一次分区操作，找到基准元素③ 递归调用分区函数：将基准元素的左边、右边部分分别传入递归函数进行排序
'''def Partition(arr, left, right):idx = random.randint(left, right)arr[left], arr[idx] = arr[idx], arr[left]l = leftr = rightx = arr[l]while l < r:while l < r and x < arr[r]:r -= 1if l < r:arr[l], arr[r] = arr[r], arr[l]l += 1while l < r and x > arr[l]:l += 1if l < r:arr[l], arr[r] = arr[r], arr[l]r -= 1return ldef quickSort(arr, l, r):if l >= r:returnnode = self.quickSort(l, r)self.quickSort(arr, l, node-1)self.quickSort(arr, node+1, r)return arr

桶排序回顾

① 初始化桶和频率数组： 创建字符长度+1的桶bucket，索引 i 表示频率为 i 的字符列表；长度为max的频率数组count，用于记录每个字符的出现次数

② 统计字符频率：通过 ord(char) 获取字符的ASCII码，作为频率数组的索引

③ 将字符按照频率放入桶中：遍历频率数组，将每个字符以频率作为索引放入数组中

④ 返回桶数组：返回桶数组，其中每个桶包含对应频率的字符列表

def bucketSort(arr, max_val):  # 移除 max_val 表示字符编码最大值（如 256）n = len(arr)# 初始化桶：索引范围 [0, max_val-1]bucket = [[] for _ in range(max_val)]# 分布：按字符编码放入桶for char in arr:bucket[ord(char)].append(char)  # 索引 = 字符编码值# 合并桶（索引升序即字符升序）sorted_arr = []for b in bucket:sorted_arr.extend(b)  # 每个桶内元素已按插入顺序排列return sorted_arr  # 返回排序后的一维数组

基数排序

① 初始化参数和辅助数组：设置最大元素数MAX_N为 50000，最大位数MAX_T为 8，进制BASE为 10；计算并存储基数的各次幂（如 10⁰, 10¹, ..., 10⁷）到数组PowOfBase中

② 预处理数组元素：为每个元素加上BASE^(MAX_T-1)（即 10⁷），确保所有元素变为正数；这一步是为了处理可能的负数输入，将其转换为正数进行排序

③ 按位进行多轮排序：从最低有效位（个位）开始，逐位进行处理（共进行MAX_T轮）

分配阶段：将元素分配到对应的桶（0-9）中对每个元素，计算当前位上的数字（通过整除和取模运算）

收集阶段：按桶的顺序（0 到 9）依次收集元素；将收集的元素依次放回原数组，覆盖原有的顺序

④ 恢复原始数值：排序完成后，从每个元素中减去BASE^(MAX_T-1)（即 10⁷）；恢复元素的原始值，完成排序过程

'''
基数排序① 初始化参数和辅助数组：设置最大元素数MAX_N为 50000，最大位数MAX_T为 8，进制BASE为 10；计算并存储基数的各次幂（如 10⁰, 10¹, ..., 10⁷）到数组PowOfBase中② 预处理数组元素：为每个元素加上BASE^(MAX_T-1)（即 10⁷），确保所有元素变为正数；这一步是为了处理可能的负数输入，将其转换为正数进行排序③ 按位进行多轮排序：从最低有效位（个位）开始，逐位进行处理（共进行MAX_T轮）分配阶段：将元素分配到对应的桶（0-9）中对每个元素，计算当前位上的数字（通过整除和取模运算）收集阶段：按桶的顺序（0 到 9）依次收集元素；将收集的元素依次放回原数组，覆盖原有的顺序④ 恢复原始数值：排序完成后，从每个元素中减去BASE^(MAX_T-1)（即 10⁷）；恢复元素的原始值，完成排序过程
'''MAX_N = 50000    # 最多的元素数MAX_T = 8        # 元素的最大位数BASE = 10        # 定义数字的进制def RedixSort(self, arr):n = len(arr)PowOfBase = [1 for i in range(self.MAX_T)]    # 代表BASE的多少次方for i in range(1, self.MAX_T):PowOfBase[i] = PowOfBase[i - 1] * self.BASEfor i in range(n):arr[i] += PowOfBase[self.MAX_T - 1]pos = 0 while pos < self.MAX_T:RedixBucket = [ [] for i in range(self.BASE)]for i in range(n):rdx = arr[i] // PowOfBase[pos] % self.BASERedixBucket[rdx].append( arr[i] )top = 0for i in range(self.BASE):for rb in RedixBucket[i]:arr[top] = rbtop += 1pos += 1for i in range(n):arr[i] -= PowOfBase[self.MAX_T - 1]return arr

一、问题描述

二叉堆的数据结构其实是基于一种叫做完全二叉树的数据结构

对于一个容器，有三种操作：

① I a：插入一个值为 a 的元素

② Q：查询最大的元素

③ D：删除最大的元素

二、算法对比

1.朴素算法

① 数组模拟容器

插入 I a—— O(1)

删除 D —— O(n)

查找 Q —— O(n)

② 有序数组模拟容器

插入 I a —— O(n)、

删除 D —— O(1)

查找 Q —— O(1)

2.二叉堆

① 二叉堆特点

Ⅰ、O(1)时间获取最大值

Ⅱ、O(logn)时间进行元素的增删

Ⅲ、利用数组随机访问的特性模拟二叉树

Ⅳ、需要有数据结构中二叉树的概念基础

② 数组表示二叉树

parent(id) = (id - 1) / 2、 left(id) = id * 2 + 1、 right(id) = id * 2 + 2

左子节点一定是个奇数，右子节点一定是个偶数

③ 堆

堆满足任意一个节点都比其子节点大 / 小

④ 大顶堆

任意一个节点的值都比其子节点大

⑤ 小顶堆

任意一个节点的值都比其子节点小

⑥ 元素插入

往数组尾部插入一个元素；对插入的元素，比较它（在树型结构中）和它的父节点的大小关系，来决定是否和父节点进行交换

插入的情况，新插入节点只会上浮，不会下沉

⑦ 获取堆顶

返回数组中的第0个元素

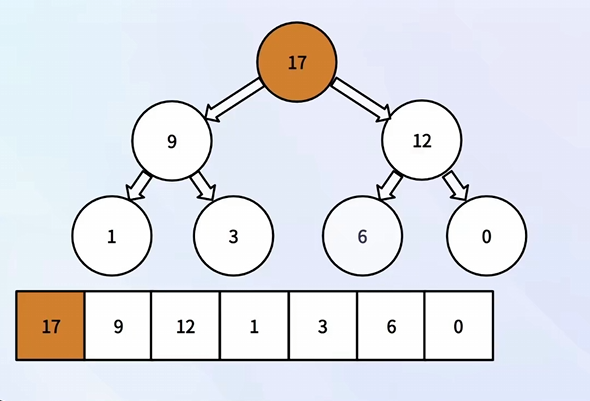
⑧ 堆顶元素删除

获取数组中的最后一个元素，然后让堆顶元素与最后一个元素进行交换

将交换后的堆顶的元素不断做“下沉”操作，选择大的进行交换，直到“交换后的堆顶的元素自己”成为最大的

删除数组的最后一个元素

三、代码分析

1.工具函数

给定一个元素下标，获取左子树下标

def lson(idx)return 2 * idx + 1

给定一个元素下标，获取右子树下标

def rson(idx):return 2 * idx + 2

给定一个元素下标，获取父节点的下标

def parrent(idx):return (idx - 1) / 2

判断函数，任意传入两个元素，返回两节点中更优的值，如果是小顶堆，则返回 a < b

# <: 小顶堆    >：大顶堆
def batter(a, b):return a > b# return a < b

2.调整大顶堆函数

Ⅰ、计算子节点索引

leftSon(curr) 和 rightSon(curr) 分别计算当前节点的左右子节点索引。

optId 初始化为当前节点索引，用于记录最大值的位置。

Ⅱ、找出最大值索引

比较当前节点与左右子节点的值：如果左子节点存在且值更大，则更新 optId 为左子节点索引。同理，对右子节点进行相同比较。better 函数默认实现为 a > b，确保构建最大堆。

Ⅲ、交换并递归调整

如果最大值不在当前节点（curr != optId），则交换当前节点与最大值节点。

递归调用 Heapify 处理被交换的子节点，确保其所有子树仍满足堆性质。

def Heapify(self, heap, size, curr):leftSonId = leftSon(curr)rightSonId = rightSon(curr)optId = currif leftSonId < size and better(heap[leftSonId], heap[optId]):optId = leftSonIdif rightSonId < size and better(heap[rightSonId], heap[optId]):optId = rightSonIdif curr != optId:heap[curr], heap[optId] = heap[optId], heap[curr]self.Heapify(heap, size, optId)

3.堆排序流程

Ⅰ、构建最大堆

从最后一个非叶子节点（n//2 -1）开始，向上逐个调用Heapify，确保整个数组成为最大堆。

Ⅱ、交换元素并调整堆

循环过程：将堆顶元素（最大值）与当前未排序部分的最后一个元素交换；减少堆的大小（size = i），将最大值排除在后续调整范围外；调用 Heapify(0) 重新调整剩余元素为最大堆。

效果：每次循环将当前最大值移至数组末尾，最终形成升序排列。

    def sortArray(self, nums: List[int]) -> List[int]:n = len(nums)for i in range(n // 2, -1, -1):self.Heapify(nums, n, i)for i in range(n-1, -1, -1):nums[0], nums[i] = nums[i], nums[0]self.Heapify(nums, i, 0)return nums

四、实战练习

912. 排序数组

给你一个整数数组 nums，请你将该数组升序排列。

你必须在 不使用任何内置函数 的情况下解决问题，时间复杂度为 O(nlog(n))，并且空间复杂度尽可能小。

示例 1：
输入：nums = [5,2,3,1]
输出：[1,2,3,5]
示例 2：
输入：nums = [5,1,1,2,0,0]
输出：[0,0,1,1,2,5]
提示：

1 <= nums.length <= 5 * 104
-5 * 104 <= nums[i] <= 5 * 104

思路与算法

辅助函数（节点关系）：

leftSon(idx)：返回节点idx的左子节点索引（2*idx + 1）。

rightSon(idx)：返回节点idx的右子节点索引（2*idx + 2）。

parent(idx)：返回节点idx的父节点索引（(idx-1)//2）。

better(a, b)：比较函数，默认返回a > b，用于定义最大堆的比较规则。

Heapify 函数：

Ⅰ、计算子节点索引