【数据结构】_排序

【本节目标】
- 排序的概念及其运用
- 常见排序算法的实现
- 排序算法复杂度及稳定性分析
1.排序的概念及其运用
1.1排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
1.2特性及分类
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
1.3常见的排序算法

2.常见排序算法的实现
2.1 插入排序
2.1.1基本思想:
直接插入排序是一种简单的插入排序法,其基本思想是:
把
待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
2.1.2直接插入排序

单趟排序(排一个数据)
//单趟排序
void InsertSort(int* a, int n)
{assert(a);int end;//有序序列最后一个下标int tmp = a[end + 1];//先保存下标为end后面那个数字,也就是要插入的数字while (end >= 0)//=0表示极端,也就是要插入的数比任何一个都小{if (tmp < a[end]){a[end + 1] = a[end];//end挪动到end+1处end--;}else{break;}}a[end + 1] = tmp;//把tmp这个要插入的数放到下标为end的后面end+1处
}
多趟排序(在单趟排序的基础上加上一个for循环)
void InsertSort(int* a, int n)
{assert(a);for (int i = 0; i < n - 1; i++){int end = i;//i表示已排序部分的最后一个元素的下标int tmp = a[end + 1];//先保存下标为end后面那个数字,也就是要插入的数字while (end >= 0)//=0表示极端,也就是要插入的数比任何一个都小{if (tmp < a[end]){a[end + 1] = a[end];//end挪动到end+1处end--;}else{break;}}a[end + 1] = tmp;//把tmp这个要插入的数放到下标为end的后面end+1处}
}
🤔🤔思考:
这里
for循环为什么是i<n-1呢?

运行结果:

2.1.3 希尔排序
希尔排序法又称缩小增量法。希尔排序法的基本思想是:通过将
原始数组分成多个子序列进行局部插入排序,逐步缩小子序列的间隔(增量),最终使整个数组基本有序,最后进行一次完整的插入排序。(希尔排序是在直接插入排序的基础上优化)
其分为两个步骤:
-
预排序(数组接近有序)
gap>1
预排序:把间距为gap的值分为一组,进行插入排序 -
直接插入排序
gap==1
由上可知,gap的核心原理为:
gap越
大,前面大的数据可以越快到后面,后面小的数,可以越快到前面。gap越大,越不接近有序;gap越小越接近有序。如果gap==1其实就相当于直接插入排序,就有序了
画图分析:

代码解析:
// 希尔排序
void ShellSort(int* a, int n)
{//1.gap>1相当于预排序,让数组接近有序//2,gap == 1就相当于直接插入排序,保证有序int gap = n;while (gap > 1){gap = gap / 3 + 1;//希尔研究发现三倍三倍走好一点;+1保证最后一次一定是1//多组并排// 对间隔为gap的所有子序列进行插入排序for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];// 对当前子序列进行插入排序while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];//往后挪 元素后移gap位end -= gap;//end往前走 向前移动gap位继续比较}else{break;}}a[end + gap] = tmp;//插入元素}}
}
🤔🤔🤔思考:为什么循环条件需要
i < n - gap
因为int end = i;和int tmp = a[end + gap];这两段代码表明i从0开始下标索引,i=end,所以假设gap=4并且一共有10个数,那么当i循环到6时,i+gap=10;下标为10的时候,已超出范围,所以会造成越界访问,所以这时候i<n-gap==10-4=6,也就是i<6时这样才不会越界访问;至于为什么要这个关于i的循环??那其实是为了实现多组并排!!
1.防止数组越界
核心问题是:当我们访问
a[i+gap]时,必须确保i+gap是一个有效的数组索引。
-
数组索引范围:
0到n-1 -
所以必须保证:
i + gap≤n - 1 -
推导出:
i≤n - 1 - gap -
在循环中我们写成:
i < n - gap(因为从0开始)
2.具体例子说明
假设有一个数组,
n = 8,当前gap = 3:
- 索引: 0 1 2 3 4 5 6 7
- 值: [5,3,8,9,1,2,7,4]
- 计算n - gap = 8 - 3 = 5,所以循环条件是
i < 5,即i从0到4。
让我们看看每次循环时
i+gap的值:
| i | i+gap | 比较的元素对 |
|---|---|---|
| 0 | 3 | a[0]和a[3] → 5和9 |
| 1 | 4 | a[1]和a[4] → 3和1 |
| 2 | 5 | a[2]和a[5] → 8和2 |
| 3 | 6 | a[3]和a[6] → 9和7 |
| 4 | 7 | a[4]和a[7] → 1和4 |
如果循环条件是i < 6(即i最大到5):
- 当
i=5时,i+gap=8,但数组最大索引是7,这就越界了!
🤔🤔🤔那为什么要:gap = gap / 3 + 1;
研究表明,gap 按3倍递减 的效率较高(比常见的2倍递减更快)。这是经验性的结论,由希尔排序的研究者提出。
+1 是为了保证 最后一次gap一定是 1,从而确保最终进行一次完整的插入排序。
2.2 选择排序
2.2.1基本思想:
每一次从
待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
2.2.2 直接选择排序

void SelectSort(int* a, int n)
{int begin = 0;while (begin < n - 1){int min = begin;//假设第一个下标为最小值//循环遍历看看有没有更小的,以自身为起点for (int i = begin; i < n; i++){if (a[i] < a[min]){min = i;}}Swap(&a[begin], &a[min]);//交换的是假设的最小的和实际的最小的begin++;}
}上面选择的是选一个值,下面我们就优化一下选两个值:
这里我们用的方法是:选出小的数放左边,选出大的数放右边;然后再缩小区间,但是我们会发现,选出之后那个数就被覆盖了,会找不到,因此这里我们就要用下标来做
// 选择排序
void SelectSort(int* a, int n)
{assert(a);//区间定义 定义两个下标int begin = 0;int end = n - 1;//还未相遇while (begin < end){//在[begin,end]之间找到最小的数和最大的数的下标int mini = begin;int maxi = begin;for (int i = begin+1; i <= end; i++)//i<=end表示在这个区间之中选择;begin+1是因为begin已经给了第一个值,那就从其后一个位置开始走{if (a[i] > a[maxi]){maxi = i;//说明i位置这个值更大}if (a[i] < a[mini]){mini = i;}}//交换排升序Swap(&a[begin], &a[mini]);//如果maxi和begin位置重叠,则maxi的位置需要修正if (begin == maxi){maxi = mini;}Swap(&a[end], &a[maxi]);begin++;end--;}
}
🤔🤔🤔思考:为什么要下面这串代码?
//如果maxi和begin位置重叠,则maxi的位置需要修正
if (begin == maxi)
{maxi = mini;
}

2.2.3 堆排序
堆排序(Heapsort)是指利用
堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
// 堆排序
void AdjustDwon(int* a, int n, int root)
{//向下调整算法int parent = root;//找出左右孩子中大的那一个int child = parent * 2 + 1;//child先指向左孩子while (child < n){//如果右孩子if (child + 1<n && a[child + 1]>a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
void HeapSort(int* a, int n)
{//排升序,建大堆//倒数第一个叶子节点for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDwon(a, n, i);}int end = n - 1;//先把最大的数换到最后while (end > 0){Swap(&a[0], &a[end]);AdjustDwon(a, end, 0);end--;}
}
2.3 交换排序
基本思想:所谓交换,就是根据序列中
两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。
2.3.1冒泡排序
// 冒泡排序
void BubbleSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){for (int j = 0; j < n - 1 - i; j++){if (a[j] > a[j + 1]){Swap(&a[j], &a[j + 1]);}}}
}
2.3.2 快速排序
(1)左右指针法

// 快速排序递归实现//获取三数取中的下标(防止栈溢出)
int GetMidIndex(int* a, int begin, int end)
{int mid = (begin + end) / 2;//找3个数里面不是最大也不是最小数的下标if (a[begin] < a[mid]){if (a[mid] < a[end]){return mid;}else if (a[begin] > a[end]){return begin;}else{return end;}}else//a[begin] > a[mid]{if (a[end] > a[mid]){return end;}else if (a[begin] < a[mid]){return begin;}else{return end;}}
}// 单趟排序
int PartSort1(int* a, int begin, int end)
{//int key = a[end];//假设key位置在右边int keyindex = end;//下标keyint midIndex = GetMidIndex(a, begin, end);Swap(&a[midIndex], &a[end]);//确保这个中间值做key在右边while (begin < end)//未相遇{//key在右边,那就左边先走,也就是begin先走//begin找大while (begin < end && a[begin] <= a[keyindex]){begin++;}//end找小while (begin < end && a[end] >= a[keyindex]){end--;}Swap(&a[begin], &a[end]);}Swap(&a[begin], &a[keyindex]);return begin;
}// 快速排序hoare版本
int QuickSort1(int* a, int left, int right)
{assert(a);if (left >= right){return;}int div = PartSort1(a, left, right);//div有划分意思,先走一个单趟排序//这时就划分成了三部分[left,div-1] div [div+1,right]QuickSort1(a, left, div - 1);QuickSort1(a, div + 1, right);}
整体结构
GetMidIndex函数:实现"三数取中"策略,选择begin、mid、end三个位置中的中间值作为基准,避免最坏情况。

PartSort1函数:实现单趟排序(分区操作),返回基准值的最终位置。

QuickSort1函数:递归实现快速排序的主函数。

(2)挖坑法

// 快速排序递归实现//获取三数取中的下标(防止栈溢出)
int GetMidIndex(int* a, int begin, int end)
{int mid = (begin + end) / 2;//找3个数里面不是最大也不是最小数的下标if (a[begin] < a[mid]){if (a[mid] < a[end]){return mid;}else if (a[begin] > a[end]){return begin;}else{return end;}}else//a[begin] > a[mid]{if (a[end] > a[mid]){return end;}else if (a[begin] < a[mid]){return begin;}else{return end;}}
}//2.挖坑法
int PartSort2(int* a, int begin, int end)
{//三数取中int midIndex = GetMidIndex(a, begin, end);Swap(&a[midIndex], &a[end]);//确保这个中间值做key在右边//坑int key = a[end];//保存坑这个值while (begin < end){//begin找比key大的while (begin < end && a[begin] <= key){begin++;}//找到后填到坑里,begin位置就形成了新的坑a[end] = a[begin];//右边找小while (begin < end && a[end] >= key){end--;}//右边找到比key小的填到左边的坑,end位置就形成的新的坑a[begin] = a[end];}a[begin] = key;//begin和end相遇后,找不到了就把key填到这个坑里return begin;//begin和end都行}void QuickSort1(int* a, int left, int right)
{assert(a);if (left >= right){return;}int div = PartSort2(a, left, right);//div有划分意思,先走一个单趟排序//这时就划分成了三部分[left,div-1] div [div+1,right]QuickSort1(a, left, div - 1);QuickSort1(a, div + 1, right);}
其他的不变,就是改了一个
PartSort2部分
(3)前后指针法
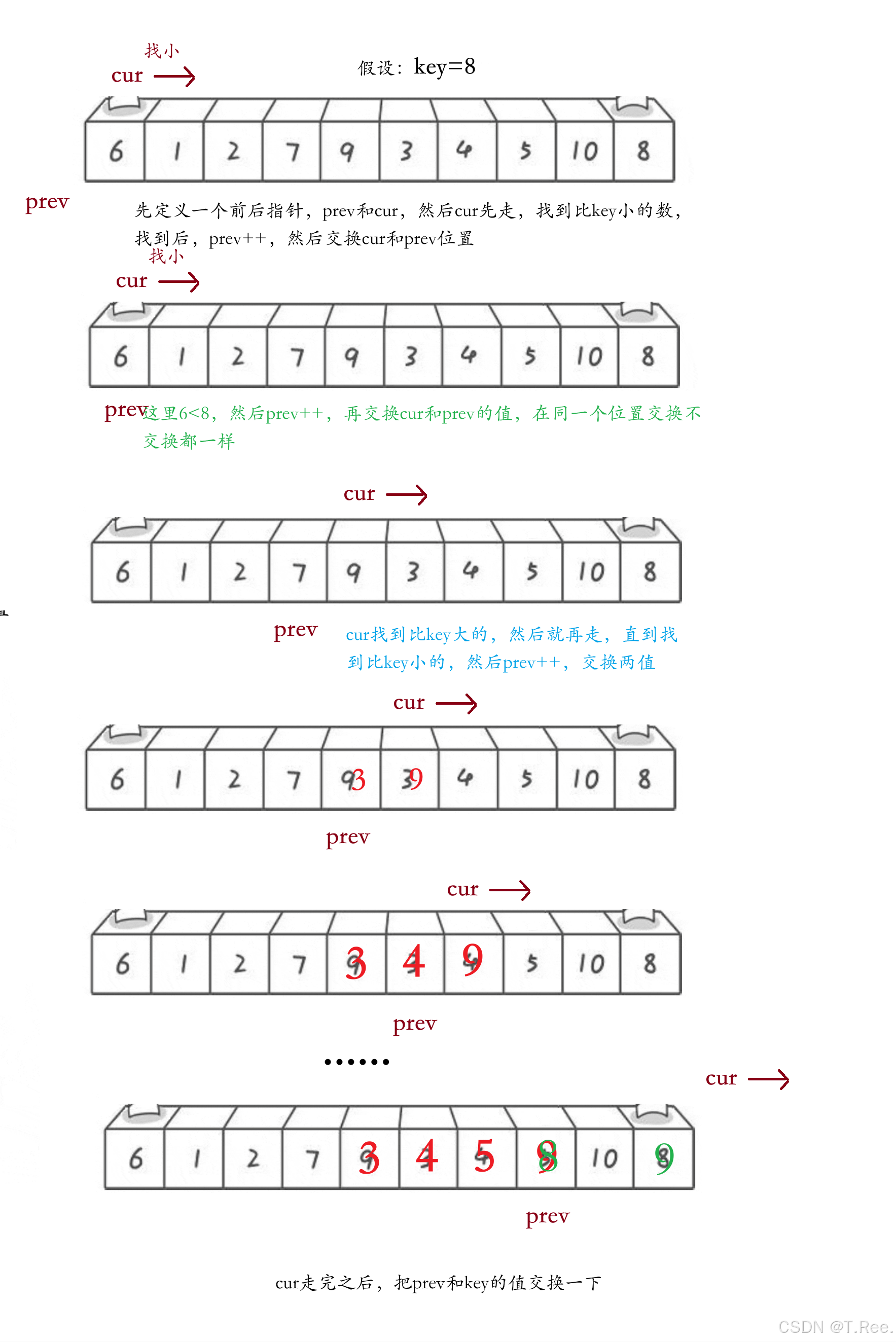
//3.前后指针法
int PartSort3(int* a, int begin, int end)
{int prev = begin - 1;int cur = begin;int keyindex = end;while (cur < end){if (a[cur] < a[keyindex] && ++prev != cur)//注意这里prev先++,因为相等交不交换都一样{Swap(&a[prev], &a[cur]);}cur++;}//交换完以后,将prev先++,再和key交换Swap(&a[++prev], &a[keyindex]);return prev;//返回这个分界点
}
2.3.3 快速排序非递归
递归改非递归:
1、改循环(斐波那契数列求解)一些简单递归才能改循环
2、栈模拟存储数据非递归
非递归的好处:
1、提高效率(递归建立栈帧还是有消耗的,但是对于现代的计算机,这个优化微乎其微可以忽略不计)
2、递归最大缺陷是,如果栈帧的深度太深,可能会导致栈溢出。因为系统栈空间一般不大在M(兆)级别
数据结构栈模拟非递归,数据是存储在堆上的,堆是G级别的空间
//快速排序非递归实现
void QuickSortNonR(int* a, int left, int right)
{//栈模拟实现Stack st;StackInit(&st);StackPush(&st, right);//先入右,先出的就是左StackPush(&st, left);while (!StackEmpty(&st)){int begin = StackTop(&st);//栈顶就是左StackPop(&st);int end = StackTop(&st);//左出完就是右(因为入栈时是个区间,所以要入两个数)StackPop(&st);//[begin,end]int div = PartSort3(a, begin, end);//单趟排序//[begin,div-1] div [div+1,end]//先处理右,再处理左if (div + 1 < end){//入栈StackPush(&st, end);StackPush(&st, div + 1);}if (begin < div - 1){//入栈StackPush(&st, div - 1);StackPush(&st, begin);}}StackDestory(&st);
}2.4 归并排序

2.4.1递归实现
void _MergeSort(int* a, int left, int right, int* tmp)
{if (left >= right){return;}//分割int mid = (left + right) / 2;//[left,mid] [mid+1,right]有序,则可以合并,现在他们没有序,子问题解决_MergeSort(a, left, mid, tmp);_MergeSort(a, mid+1, right, tmp);//归并[left,mid] [mid+1,right]有序int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;// 声明并初始化index变量,指向当前子数组的起始位置int index = left;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}//把归并好的在tmp的数据再拷贝回到原数组for (int i = left; i <= right; i++){a[i] = tmp[i];}
}//归并排序递归实现
void MergeSort(int* a, int n)// a 是待排序数组,n 是数组长度。
{assert(a);int* tmp = malloc(sizeof(int) * n);_MergeSort(a, 0, n - 1, tmp);free(tmp);//功能:分配一个与原数组大小相同的临时数组 tmp,调用递归排序函数,最后释放临时内存。
}
归并排序的基本思想
- 分解(Divide):将数组
分成两个子数组,递归地对每个子数组进行排序。 - 合并(Conquer):将两个
已排序的子数组合并成一个有序数组。
归并排序由两个主要函数组成:
MergeSort:对外接口,分配临时数组并调用递归函数。_MergeSort:递归实现排序和合并逻辑。

举例说明:

2.4.2非递归实现
归并排序的核心思想是分治法,将数组分成两个子数组,分别排序后再合并。非递归版本通过迭代方式,逐步增大子数组的规模,直到整个数组有序。

//用于合并两个已排序的子数组
void MergeArr(int* a, int begin1, int end1, int begin2, int end2,int* tmp)
{int left = begin1;int right = end2;int index = begin1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}//把归并好的在tmp的数据再拷贝回到原数组for (int i = left; i <= right; i++){a[i] = tmp[i];}
}// 归并排序非递归实现
void MergeSortNonR(int* a, int n)
{assert(a);int* tmp = malloc(sizeof(int) * n);int gap = 1;//间距为1 一个一个归并while (gap<n){for (int i = 0; i < n; i += 2 * gap){//[i, i + gap-1)[i + gap, i + 2 * gap-1)闭区间int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;//1、合并时只有第一组,就不需要合并if (begin2 >= n){break;}//2、合并时第二组只有部分数据,需要修正end2边界if (end2 >= n){end2 = n - 1;}MergeArr(a, begin1, end1, begin2, end2, tmp);}PrintArray(a, n);gap *= 2;}free(tmp);
}
MergeArr函数
思考:
MergeSortNonR这个函数里面为什么要修正边界
在MergeSortNonR函数中修正边界是为了处理数组长度不是2的幂时的特殊情况。归并排序的非递归实现通过迭代逐步合并相邻的子数组,每次迭代中子数组的大小(gap)翻倍。当子数组大小超过数组长度的一半时,可能会出现以下两种边界情况:


2.5 非比较排序
💡💡思想:计数排序又称为
鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤:
- 统计
相同元素出现次数 - 根据统计的结果将序列回收到原来的序列中
(计数排序只适用于整形,如果浮点数或者字符串排序,还得用比较排序)

❗❗❗注意:这下面的代码写的是绿色框里面的相对位置法
// 计数排序
void CountSort(int* a, int n)
{assert(a);//分别求出最小数和最大数int min = a[0];int max = a[0];//求范围for (int i = 1; i < n; i++){if (a[i] > max){max = a[i];}if (a[i] < min){min = a[i];}}int range = max - min + 1;//求的是范围//为什么要+1呢?//因为假设最大值9,最小值0;9-0=9但实际是10个数据int* countArr = (int*)malloc(sizeof(int) * range);//开辟一个数组容纳空间memset(countArr, 0, sizeof(int) * range);//初始化//统计次数for (int i = 0; i < n; i++){//对应值就在其对应位置加加countArr[a[i] - min]++;//这里是相对位置(减去最小值的位置)//假设a[0]=1000,1000-1000=0;那么就在这个新开的countArr[0]处++}//排序int index = 0;for (int j = 0; j < range; j++){while (countArr[j]--){a[index++] = j + min;//j+min表示对应的值,这里是放到新数组a里面}}free(countArr);
}
🎉🎉🎉
友友们
到这里我们就结束啦~
我们下期见噢~

相关文章:

【数据结构】_排序
【本节目标】 排序的概念及其运用常见排序算法的实现排序算法复杂度及稳定性分析 1.排序的概念及其运用 1.1排序的概念 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。 1.2特性…...

《前端面试题:JS数据类型》
JavaScript 数据类型指南:从基础到高级全解析 一、JavaScript 数据类型概述 JavaScript 作为一门动态类型语言,其数据类型系统是理解这门语言的核心基础。在 ECMAScript 标准中,数据类型分为两大类: 1. 原始类型(Pr…...

PPT转图片拼贴工具 v4.3
软件介绍 这个软件就是将PPT文件转换为图片并且拼接起来。 效果展示 支持导入文件和支持导入文件夹,也支持手动输入文件/文件夹路径 软件界面 这一次提供了源码和开箱即用版本,exe就是直接用就可以了。 软件源码 import os import re import sys …...

Chrome安装代理插件ZeroOmega(保姆级别)
目录 本文直接讲解一下怎么本地安装ZeroOmega一、下载文件在GitHub直接下ZeroOmega 的文件(下最新版即可) 二、安装插件打开 Chrome 浏览器,访问 chrome://extensions/ 页面(扩展程序管理页面),并打开开发者…...

Transformer-BiGRU多变量时序预测(Matlab完整源码和数据)
Transformer-BiGRU多变量时序预测(Matlab完整源码和数据) 目录 Transformer-BiGRU多变量时序预测(Matlab完整源码和数据)效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab实现Transformer-BiGRU多变量时间序列预测&…...

新华三H3CNE网络工程师认证—Easy IP
Easy IP 就是“用路由器自己的公网IP,给全家所有设备当共享门牌号”的技术!(省掉额外公网IP,省钱又省配置!) 生活场景对比,想象你住在一个小区:普通动态NAT:物业申请了 …...

《视觉SLAM十四讲》自用笔记 第二讲:SLAM系统概述
在rm队伍里作为算法组梯队队员度过了一个赛季,为了促进和负责其他工作的算法组成员的交流,我决定在接下来的半个学期里(可能更快)读完这本书,并将其中的部分理论应用于我自制的雷达导航小车上。 以下为第二讲的部分笔记…...

vscode 插件 eslint, 检查 js 语法
1. 起因, 目的: 我的需求 vscode 写js代码, 有什么插件能进行语法检查。 比如某个函数没有定义,getName(), 但是却调用了。 那么这个插件会给出警告,在 getName() 给出红色波浪线。类似这种效果的插件, 有吗…...

Excel 模拟分析之单变量求解简单应用
正向求解 利用公式根据贷款总额、还款期限、贷款利率,求每月还款金额 反向求解 根据每月还款能力,求最大能承受贷款金额 参数: 目标单元格:求的值所在的单元格 目标值:想要达到的预期值 可变单元格:变…...

装备制造项目管理具备什么特征?如何选择适配的项目管理软件系统进行项目管控?
国内某大型半导体装备制造企业与奥博思软件达成战略合作,全面引入奥博思 PowerProject 打造企业专属项目管理平台,进一步提升智能制造领域的项目管理效率与协同能力。 该项目管理平台聚焦半导体装备研发与制造的业务特性,实现了从项目立项、…...

FPGA 动态重构配置流程
触发FPGA 进行配置的方式有两种,一种是断电后上电,另一种是在FPGA运行过程中,将PROGRAM 管脚拉低。将PROGRAM 管脚拉低500ns 以上就可以触发FPGA 进行重构。 FPGA 的配置过程大致可以分为:配置的触发和建立阶段、加载配置文件和建…...
介绍)
Elasticsearch的审计日志(Audit Logging)介绍
Elasticsearch 的审计日志(Audit Logging)是一种记录与安全相关事件的功能,用于监控和追踪对集群的访问行为。通过审计日志,管理员可以了解谁在何时对哪些资源执行了什么操作,从而满足合规性要求、进行安全分析和排查异常行为。 一、审计日志的核心功能 记录安全事件捕获…...

软件测试:质量保障的基石与未来趋势
软件测试作为软件开发生命周期中的关键环节,不仅是发现和修复缺陷的手段,更是确保产品质量、提升用户体验和降低开发成本的重要保障。在当今快速迭代的互联网时代,测试已从单纯的验证活动演变为贯穿整个开发过程的质量管理体系。本文将系统阐…...

网络安全逆向分析之rust逆向技巧
rust逆向技巧 rust逆向三板斧: 快速定位关键函数 (真正的main函数):观察输出、输入,字符串搜索,断点等方法。定位关键 加密区 :根据输入的flag,打硬件断点,快速捕获程序中对flag访问的位置&am…...

Docker容器化技术概述与实践
哈喽,大家好,我是左手python! Docker 容器化的基本概念 Docker 容器化是一种轻量级的虚拟化技术,通过将应用程序及其依赖项打包到一个可移植的容器中,使其在任何兼容 Docker 的环境中都能运行。与传统的虚拟机技术不同…...

win中将pdf转为图片
0 资料 博客 1 正文 直接使用这个软件即可https://sourceforge.net/projects/pkpdfconverter/...

Leetcode 2494. 合并在同一个大厅重叠的活动
1.题目基本信息 1.1.题目描述 表: HallEvents ----------------- | Column Name | Type | ----------------- | hall_id | int | | start_day | date | | end_day | date | ----------------- 该表可能包含重复字段。 该表的每一行表示活动的开始日期和结束日期&…...

vue+elementui 网站首页顶部菜单上下布局
菜单集合后台接口动态获取,保存到store vuex状态管理器 <template><div id"app"><el-menu:default-active"activeIndex2"class"el-menu-demo"mode"horizontal"select"handleSelect"background-…...

网络安全-等级保护(等保) 3-3-1 GB/T 36627-2018 附录A (资料性附录) 测评后活动、附 录 B (资料性附录)渗透测试的有关概念说明
################################################################################ GB/T 36627-2018 《信息安全技术 网络安全等级保护测试评估技术指南》对网络安全等级保护测评中的相关测评技术进行明确的分类和定义,系统地归纳并阐述测评的技术方法,概述技术性安全测试和…...

pytorch3d+pytorch1.10+MinkowskiEngine安装
1、配置pytorch1.10cuda11.0 pip install torch1.10.1cu111 torchvision0.11.2cu111 torchaudio0.10.1 -f https://download.pytorch.org/whl/cu111/torch_stable.html 2、配置 MinkowskiEngine库 不按下面步骤,出现错误 1、下载MinkowskiEngine0.5.4到本地 2、查看…...
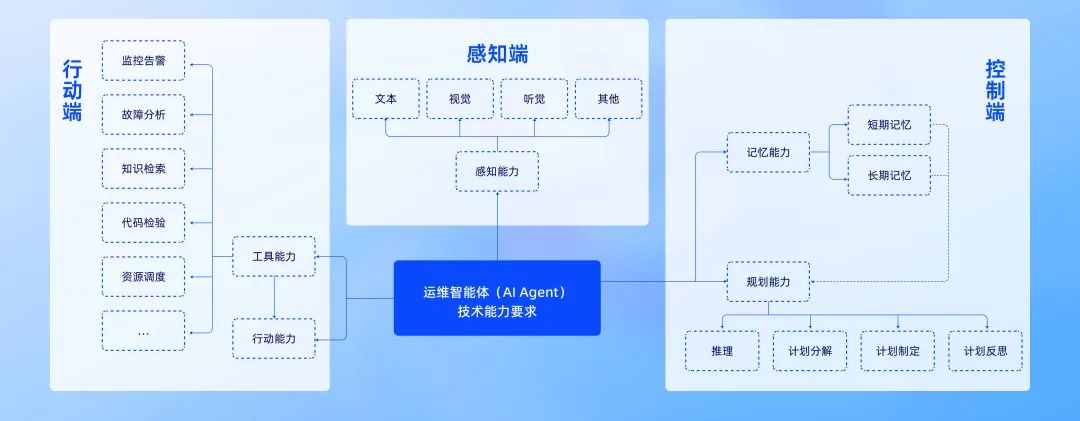
AI Infra运维实践:DeepSeek部署运维中的软硬结合
发布会资料 《AI Infra运维实践:DeepSeek部署运维中的软硬结合》 袋鼠云运维服务 1、行业痛点 随着数字化转型的深入,企业面临的运维挑战日益复杂,所依托的平台在长期使用的过程中积累了各式各样的问题或者难点。这些问题不仅影响效率&…...

MySQL体系架构解析(二):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...

深度学习在RNA分子动力学中的特征提取与应用指南
深度学习在RNA分子动力学中的特征提取与应用指南 引言:RNA结构动力学与AI的融合 RNA作为生命活动的核心分子,其动态构象变化直接影响基因调控、蛋白合成等关键生物过程。分子动力学(Molecular Dynamics, MD)模拟通过求解牛顿运动方程,可获取RNA原子级运动轨迹(时间尺度…...

K8s基础一
Kubernetes 架构 Kubernetes 背后的架构概念。 Kubernetes 集群由一个控制平面和一组用于运行容器化应用的工作机器组成, 这些工作机器称作节点(Node)。每个集群至少需要一个工作节点来运行 Pod。 工作节点托管着组成应用负载的 Pod。控制平…...

2025五大免费变声器推荐!
在游戏开黑时想靠声音搞怪活跃气氛,或是在直播中用独特声线吸引观众,又或者给视频配音时想尝试不同角色 —— 但市面上的变声软件要么收费高昂,要么效果生硬、操作复杂,难道找到一款好用又免费的变声器真的这么难? 今…...

StringRedisTemplete使用
StringRedisTemplate是Spring Data Redis提供的一个模板类,用于简化对Redis的操作。它特别适合处理字符串类型的数据,并且封装了一系列常用的Redis命令,使开发者能够以更简洁的方式进行Redis操作。本文将详细介绍 StringRedisTemplate的使用方…...

SDC命令详解:使用set_min_capacitance命令进行约束
相关阅读 SDC命令详解https://blog.csdn.net/weixin_45791458/category_12931432.html?spm1001.2014.3001.5482 目录 指定最小需驱动电容值 指定对象列表/集合 简单使用 写在最后 set_min_capacitance命令用于设置输入端口的最小需驱动电容(设置了输入端口的min_c…...

几何引擎对比:OpenCasCade、ACIS、Parasolid和CGM
概述 从技术架构与行业实践来看,OpenCasCade 凭借开源生态与轻量化设计形成差异化竞争力,尤其适合预算敏感、需定制开发或依赖开源工具链的场景;而 ACIS、Parasolid 等商业内核则通过工业级精度优化与主流 CAD 深度绑定占据大型企业市场&…...

OD 算法题 B卷【猴子吃桃】
文章目录 猴子吃桃 猴子吃桃 猴子喜欢吃桃,桃园有N棵桃树,第i棵桃树上有Ni个桃,看守将在H(>N)小时后回来;猴子可以决定吃桃的速度K(个/小时),每个小时他会选择一棵桃树,从中吃掉K个桃,如果这…...

汽车安全体系:FuSa、SOTIF、Cybersecurity 从理论到实战
汽车安全:功能安全(FuSa)、预期功能安全(SOTIF)与网络安全(Cybersecurity) 从理论到实战的安全体系 引言:自动驾驶浪潮下的安全挑战 随着自动驾驶技术从L2向L4快速演进,汽车安全正从“机械可靠…...

