几种简单的排序算法(C语言)
目录
1 简介
2 冒泡排序
2.1 基本思路
2.2 代码实现
3 选择排序
3.1 基本思路
3.2 代码实现
4 插入排序
4.1 基本思路
4.2 代码实现
5 快速排序
5.1 基本思路
5.2 代码实现
6 归并排序
6.1 基本思路
6.2 代码实现
7 基数排序
7.1 基本思路
7.2 代码实现
8 希尔排序
8.1 基本思路
8.2 代码实现
9 堆排序
9.1 基本思路
9.2 代码实现
10 总结
1 简介
在编程实践中,排序算法是基础却极其重要的一类算法,广泛应用于数据组织、查找优化和算法竞赛等多个领域。本文将系统地介绍几种常见的排序算法,包括冒泡排序、选择排序、插入排序、归并排序、快速排序、希尔排序、堆排序和基数排序,结合 C 语言代码实现,帮助读者深入理解每种排序的原理、适用场景及其性能差异。无论是初学者打基础,还是备战算法面试,本篇内容都具有较高的参考价值。
2 冒泡排序
冒泡排序(Bubble Sort)是一种简单直观的排序算法,通过不断地交换相邻逆序的元素,使较大的元素像气泡一样逐渐“冒”到序列的末尾。尽管它的性能不如高级排序算法,但因其实现简单,常用于算法入门教学或对小规模数据进行排序。
2.1 基本思路
冒泡排序通过双层循环遍历数组,外层控制排序轮数,内层逐个比较相邻元素,如果前一个元素大于后一个,则交换位置。每一轮结束后,当前未排序部分中最大的元素被移到末尾。重复该过程,直到所有元素有序。
冒泡排序
2.2 代码实现
// 冒泡排序
void bubbleSort(int *a, int n) {for (int i = 0; i < n - 1; i++) {for (int j = 0; j < n - i - 1; j++) {if (a[j] > a[j + 1]) {int temp = a[j];a[j] = a[j + 1];a[j + 1] = temp;}}}
}3 选择排序
选择排序(Selection Sort)是一种原地、稳定的排序算法。它通过在未排序区间中反复选择最小(或最大)元素,并将其放到已排序序列的末尾,逐步构建整个有序序列。该算法结构简单、易于实现,但在大数据量下效率较低。
3.1 基本思路
选择排序每一轮从未排序部分中选出最小的元素,将其与当前轮起始位置的元素交换。外层循环控制已排序与未排序区域的分界,内层循环寻找最小值的位置。随着每一轮结束,最小值被“选出”并放入正确的位置,最终实现整体有序。
选择排序
3.2 代码实现
// 选择排序
void sel(int *a, int n) {for (int i = 0; i < n - 1; i++) {int minIndex = i;for (int j = i + 1; j < n; j++) {if (a[j] < a[minIndex]) {minIndex = j;}}if (minIndex != i) {int temp = a[i];a[i] = a[minIndex];a[minIndex] = temp;}}
}4 插入排序
插入排序(Insertion Sort)是一种简单直观的排序算法,适用于小规模数据排序或基本有序的数据集合。它通过构建有序序列,将待排序元素逐个插入到已排序部分的适当位置,从而实现整体有序。插入排序是一种稳定排序,空间复杂度为 O(1)。
4.1 基本思路
从第二个元素开始,逐个将当前元素与它前面的元素进行比较,如果当前元素更小,就将前面的元素后移,直到找到合适位置后插入该元素。这个过程相当于模拟打扑克牌时整理牌的方式,不断向有序部分“插入”新的元素,直到所有元素排序完成。
插入排序
4.2 代码实现
// 插入排序
void insert(int *a, int n) {for (int i = 1; i < n; i++) {int key = a[i];int j = i - 1;while (j >= 0 && a[j] > key) {a[j + 1] = a[j];j--;}a[j + 1] = key;}
}5 快速排序
快速排序是一种采用分治法思想的高效排序算法,它通过选取一个基准元素,将待排序序列划分为左右两个子序列,其中左子序列的所有元素都不大于基准,右子序列的所有元素都不小于基准,然后递归地对这两个子序列进行快速排序。由于其在多数情况下表现优异,因此是实际应用中最常用的排序算法之一。
5.1 基本思路
快速排序的核心思路是选择一个基准元素,通过一趟扫描将数组划分为两个部分:左边是小于基准的元素,右边是大于基准的元素,然后对这两个部分分别递归执行同样的操作,最终实现整个数组的有序排列。排序过程中通常采用交换的方式在原数组上进行划分,从而实现原地排序,减少额外空间开销。
快速排序
5.2 代码实现
// 交换函数
void swap(int *a, int *b) {int temp = *a;*a = *b;*b = temp;
}// 分区函数
int partition(int *a, int low, int high) {int pivot = a[high]; // 选择最后一个元素作为基准int i = low - 1; // i 用于追踪小于基准的区间for (int j = low; j < high; j++) {if (a[j] < pivot) {i++;swap(&a[i], &a[j]);}}swap(&a[i + 1], &a[high]);return i + 1; // 返回基准的最终位置
}// 快速排序主函数
void quickSort(int *a, int low, int high) {if (low < high) {int pi = partition(a, low, high); // pi 为基准的最终位置quickSort(a, low, pi - 1); // 递归排序左子数组quickSort(a, pi + 1, high); // 递归排序右子数组}
}6 归并排序
归并排序是一种基于分治思想的稳定排序算法,它将一个数组不断二分为更小的子数组,直到每个子数组只包含一个元素,然后再将这些有序子数组两两合并为一个有序数组,最终得到排序结果。归并排序在最坏、平均和最好情况下的时间复杂度都为 O(n log n),适用于需要稳定排序且数据量较大的场景。
6.1 基本思路
归并排序首先将整个数组划分成两半,递归地对每一半进行归并排序,直到子数组长度为 1。随后,通过一个“合并过程”将两个有序子数组合并成一个新的有序数组。这个合并过程是归并排序的关键步骤,它通过比较两个子数组的元素大小并顺序地放入新数组中,最终形成排序好的数组。
归并排序
6.2 代码实现
// 合并两个有序数组
void merge(int *a, int left, int mid, int right) {int n1 = mid - left + 1;int n2 = right - mid;int *L = (int *)malloc(n1 * sizeof(int));int *R = (int *)malloc(n2 * sizeof(int));for (int i = 0; i < n1; i++) L[i] = a[left + i];for (int j = 0; j < n2; j++) R[j] = a[mid + 1 + j];int i = 0, j = 0, k = left;while (i < n1 && j < n2) {if (L[i] <= R[j]) a[k++] = L[i++];else a[k++] = R[j++];}while (i < n1) a[k++] = L[i++];while (j < n2) a[k++] = R[j++];free(L);free(R);
}// 归并排序
void mergeSort(int *a, int left, int right) {if (left < right) {int mid = (left + right) / 2;mergeSort(a, left, mid);mergeSort(a, mid + 1, right);merge(a, left, mid, right);}
}7 基数排序
基数排序(Radix Sort)是一种非比较型排序算法,适用于对整数或字符串进行排序。它通过按位分组和排序来实现整体排序,通常从最低有效位(LSD)到最高有效位(MSD)逐位排序。基数排序的时间复杂度可达到 O(k·n),其中 n 是元素个数,k 是最大元素的位数(或长度)。它适合大规模、位数不多的正整数排序。
7.1 基本思路
基数排序将所有元素按“位”进行排序,从最低位到最高位。每一轮排序都使用一个稳定的排序算法(如计数排序)对当前位进行排序。通过多轮“按位排序”后,整个数组就变得有序。因为是逐位稳定排序,所以可以避免破坏已排序好的低位顺序,从而达到全局有序。
基数排序
7.2 代码实现
// 基数排序
void countSort(int *a, int n, int exp) {int output[n];int count[10] = {0};// 统计每个桶中元素个数for (int i = 0; i < n; i++) {int digit = (a[i] / exp) % 10;count[digit]++;}// 累加,确定各桶位置for (int i = 1; i < 10; i++) {count[i] += count[i - 1];}// 从后向前遍历,稳定排序for (int i = n - 1; i >= 0; i--) {int digit = (a[i] / exp) % 10;output[count[digit] - 1] = a[i];count[digit]--;}// 拷贝结果回原数组for (int i = 0; i < n; i++) {a[i] = output[i];}
}int getMax(int *a, int n) {int max = a[0];for (int i = 1; i < n; i++) {if (a[i] > max)max = a[i];}return max;
}void radixSort(int *a, int n) {int max = getMax(a, n);for (int exp = 1; max / exp > 0; exp *= 10) {countSort(a, n, exp);}
}8 希尔排序
希尔排序是插入排序的一种优化形式,也被称为“缩小增量排序”。它通过将整个数组按照一定的间隔(gap)分组,对每组分别进行插入排序,从而减少整体移动次数。随着排序的进行,gap 逐渐缩小,最终当 gap = 1 时,整个数组基本接近有序,再进行一次插入排序即可完成排序。希尔排序的效率高于普通插入排序,尤其在处理大量数据时性能更优。
8.1 基本思路
希尔排序通过定义一个初始间隔(如 n/2),将数组分为若干个子序列,对每个子序列进行插入排序。然后不断缩小间隔(通常减半),重复上述过程,直到间隔为 1 时,执行最后一次插入排序。由于前期大间隔排序已经基本理顺了元素位置,最后的插入排序效率很高。这种逐步逼近有序的策略显著提高了整体排序性能。
8.2 代码实现
// 希尔排序
void shell(int *a, int n) {for (int gap = n / 2; gap > 0; gap /= 2) {for (int i = gap; i < n; i++) {int temp = a[i];int j;for (j = i; j >= gap && a[j - gap] > temp; j -= gap) {a[j] = a[j - gap];}a[j] = temp;}}
}9 堆排序
堆排序(Heap Sort)是一种基于堆这种数据结构的比较型排序算法。它将待排序数组构建成一个大根堆(或小根堆),使得堆顶元素为最大值(或最小值),然后将堆顶元素与堆的最后一个元素交换,缩小堆的范围,并重新调整堆结构。通过反复取出堆顶元素,最终形成有序序列。堆排序的时间复杂度为 O(n log n),不需要额外的空间,适合对大量数据进行原地排序。
9.1 基本思路
堆排序的核心在于两步操作:建堆和调整堆。首先,通过“上滤”或“下滤”方法将整个数组构建成一个最大堆(即每个父节点都大于等于其子节点);接着重复执行:将堆顶元素与末尾元素交换,然后对前 n-1 个元素重新调整为最大堆。每轮都能将当前未排序部分的最大值“沉”到末尾,最终实现整体排序。
9.2 代码实现
// 交换两个元素
void swap(int *a, int *b) {int temp = *a;*a = *b;*b = temp;
}// 调整为最大堆
void heapify(int *a, int n, int i) {int largest = i; // 假设父节点最大int left = 2 * i + 1; // 左子节点下标int right = 2 * i + 2; // 右子节点下标// 如果左子节点比父节点大if (left < n && a[left] > a[largest])largest = left;// 如果右子节点比当前最大值还大if (right < n && a[right] > a[largest])largest = right;// 如果最大值不是当前节点,交换并继续调整if (largest != i) {swap(&a[i], &a[largest]);heapify(a, n, largest);}
}// 堆排序
void heapSort(int *a, int n) {// 建堆(从最后一个非叶子节点开始)for (int i = n / 2 - 1; i >= 0; i--)heapify(a, n, i);// 逐个将最大值移到末尾,缩小堆for (int i = n - 1; i > 0; i--) {swap(&a[0], &a[i]); // 把堆顶元素放到末尾heapify(a, i, 0); // 重新对剩余元素调整为最大堆}
}
10 总结
本文系统地介绍了几种经典排序算法,包括冒泡、选择、插入、快速、归并、希尔、堆、基数排序等,结合 C 语言实现,从原理到代码细节进行了深入解析。通过对每种算法的基本思路、适用场景和时间复杂度的比较,读者可以全面了解各类排序算法的优势与局限,为日后编程实践、算法竞赛或技术面试打下坚实基础。这不仅有助于掌握排序的核心思想,也提升了解决实际问题的能力。
本文的可视化均来自于以下网址:VisuAlgo
感兴趣的可以看一下。
相关文章:
)
几种简单的排序算法(C语言)
目录 1 简介 2 冒泡排序 2.1 基本思路 2.2 代码实现 3 选择排序 3.1 基本思路 3.2 代码实现 4 插入排序 4.1 基本思路 4.2 代码实现 5 快速排序 5.1 基本思路 5.2 代码实现 6 归并排序 6.1 基本思路 6.2 代码实现 7 基数排序 7.1 基本思路 7.2 代码实现 8 …...

RTOS学习之重难点
📢:如果你也对机器人、人工智能感兴趣,看来我们志同道合✨ 📢:不妨浏览一下我的博客主页【https://blog.csdn.net/weixin_51244852】 📢:文章若有幸对你有帮助,可点赞 👍…...

有没有 MariaDB 5.5.56 对应 MySQL CONNECTION_CONTROL 插件
有没有 MariaDB 对应 MySQL CONNECTION_CONTROL 插件 背景 写这篇文章的目的是因为昨晚半夜突然被call起来,有一套系统的mysql数据库启动失败了。尝试了重启服务器也不行。让我协助排查一下问题出在哪。 分析过程 一开始拿到服务器IP地址,就去数据库…...

setting up Activiti BPMN Workflow Engine with Spring Boot
spring.activiti.database-schema-update: true Controls how Activiti handles its database tables on startup. Options: true – Default. Creates or updates tables automatically if missing. ✅ Good for development. false – Disables auto-update. Throws an err…...
)
使用 C/C++ 和 OpenCV 提取图像的感兴趣区域 (ROI)
使用 C/C 和 OpenCV 提取图像的感兴趣区域 (ROI) 在计算机视觉中,感兴趣区域 (Region of Interest, ROI) 是指从图像中选择的一个特定区域,我们希望对其进行进一步的处理或分析。例如,在人脸识别中,ROI 就是包含人脸的矩形框。Op…...

TripGenie:畅游济南旅行规划助手:个人工作纪实(二十二)
这周,我进行了历史记录的设计与制作,我对于每一个用户与智能体交互得出的历史行程的数据进行了存储与可视化展示。 首先,我设置了一个csv文件存储每一个得出的行程规划,注意这里的地图我设置了一个全路径进行存储,这样…...

如何用AI高效运营1000+Tiktok矩阵账号
在当今数字化的时代,Tiktok 矩阵账号运营成为了众多企业和个人追求流量与变现的重要手段。然而,面对众多的账号管理,如何高效运营成为了关键。此时,AI 工具的出现为我们提供了强有力的支持。 一、Tiktok 矩阵账号的重要性 Tiktok…...

杭州瑞盟 MS35774/MS35774A 低噪声256细分微步进电机驱动,用于空调风门电机驱动,香薰电机驱动
杭州瑞盟 MS35774/MS35774A 低噪声256细分微步进电机驱动,用于空调风门电机驱动,香薰电机驱动 简述 MS35774/MS35774A 是一款高精度、低噪声的两相步进 电机驱动芯片,芯片内置功率 MOSFET ,长时间工作的平均电 流可以达到 1…...

【论文解读】Toolformer: 语言模型自学使用工具
1st author: Timo Schick - Google Scholar paper: Toolformer: Language Models Can Teach Themselves to Use Tools | OpenReview NeurIPS 2023 oral code: lucidrains/toolformer-pytorch: Implementation of Toolformer, Language Models That Can Use Tools, by…...

408第一季 - 数据结构 - 线性表II
链表 头节点始终指向第一个 头节点的好处: 第一个好处 这里L是头节点 可以发现,删除第一个也可以统一了 第二个好处 这是无头节点,空和非空指向的不一样 然后有头节点就可以统一了! 双链表 插入 第一步要在第四步之前&…...

网络通讯知识——通讯分层介绍,gRPC,RabbitMQ分层
网络通讯分层 网络通讯分层是为了将复杂的网络通信问题分解为多个独立、可管理的层次,每个层次专注于特定功能。目前主流的分层模型包括OSI七层模型和TCP/IP四层(或五层)模型,以下是详细解析: 一、OSI七层模型&#…...

Linux与Windows切换使用Obsidian,出现 unexplained changes 问题的解决
如果你的Obsidian文档在Linux与Windows间来回切换,可能会涉及到文件的保存换行符问题,但这样的话就容易导致一个问题,那就是内容无差异,Obsidian却提示unexplained changes,Windows系统下的解决方法如下,找…...
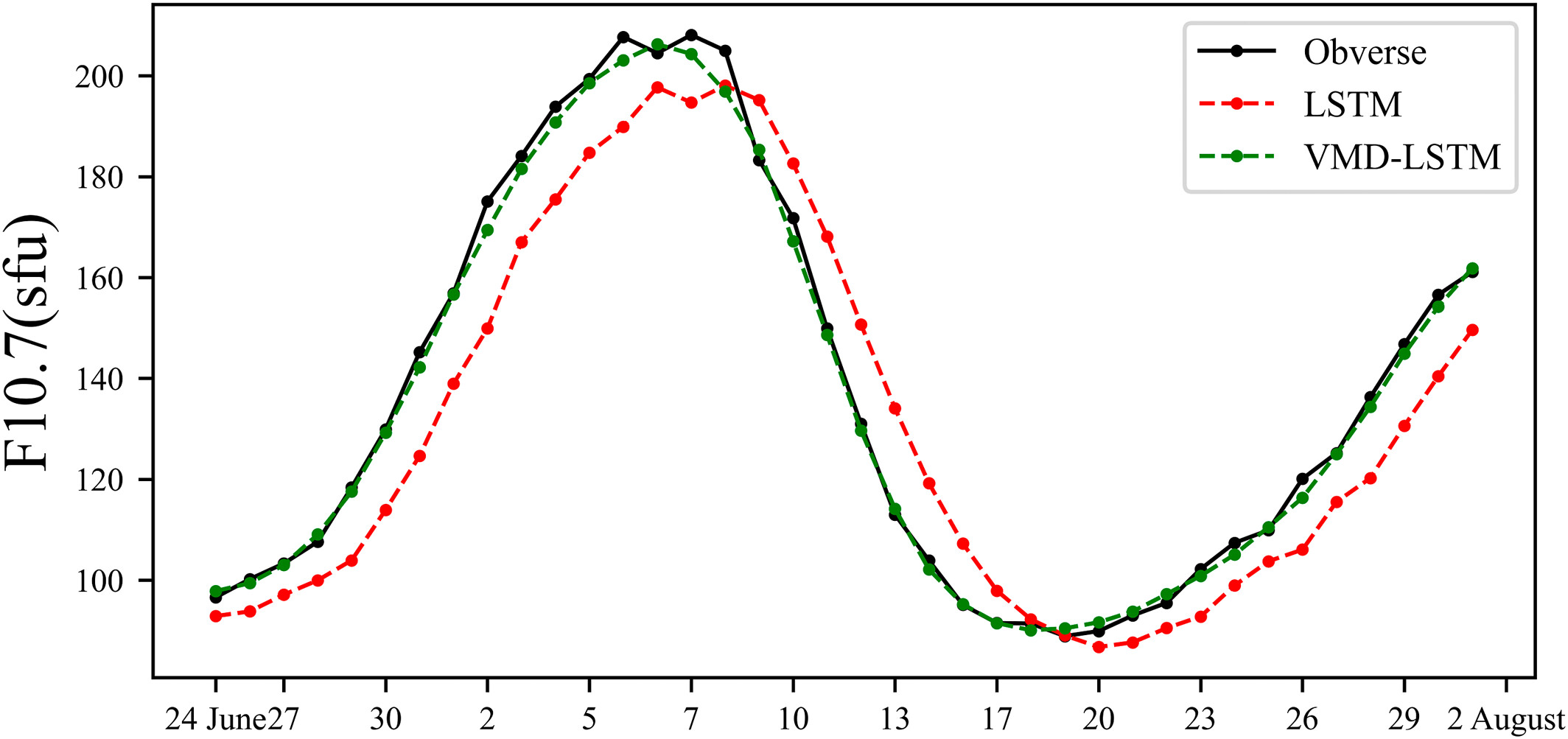
基于VMD-LSTM融合方法的F10.7指数预报
F10.7 Daily Forecast Using LSTM Combined With VMD Method F10.7 solar radiation flux is a well-known parameter that is closely linked to solar activity, serving as a key index for measuring the level of solar activity. In this study, the …...

35 C 语言字符串转数值函数详解:strtof、strtod、strtold(含 errno 处理、ERANGE 错误)
1 strtof() 函数 1.1 函数原型 #include <stdlib.h> // 必须包含这个头文件才能使用 strtof() #include <errno.h> // 包含 errno 和 ERANGE #include <float.h> // 包含 FlOAT_MAX 和 FLOAT_MIN #include <math.h> // 包含 HUGE_VALF(inf)float…...

解决 idea提示`SQL dialect is not configured` 问题
前言 在 Java 开发中,尤其是使用 IntelliJ IDEA 或 MyBatis 等框架时,开发者常会遇到 SQL dialect is not configured 的警告或错误。这一问题不仅影响代码的高亮和智能提示功能,还可能导致表结构解析失败、语法校验失效等问题。 一、问题分…...

springboot的test模块使用Autowired注入失败
springboot的test模块使用Autowired注入失败的原因: 注入失败的原因可能是用了junit4的包的Test注解 import org.junit.Test;解决方法:再加上RunWith(SpringRunner.class)注解即可 或者把Test由junit4改成junit5的注解,就不用加上RunWith&…...

日志收集工具-Filebeat
提示:windows 环境下 Filebeat 的安装与使用 文章目录 前言一、安装二、配置部署三、启动测试 前言 Filebeat 一般用于日志采集,由两部分组成 :Harvesters 和 prospector Harvesters采集器:逐行读取单个文件的内容,并…...

【PCIe总线】 -- PCI、PCIe相关实现
PCI、PCIe相关概念和知识点 【PCIe总线】-- PCI、PCIe基础知识点整理 【PCIe】非常适合初学的pcie博客(PCIe知识整理) PCIe具体实现 【PCIe】如何获取PCIe的BAR空间大小?...
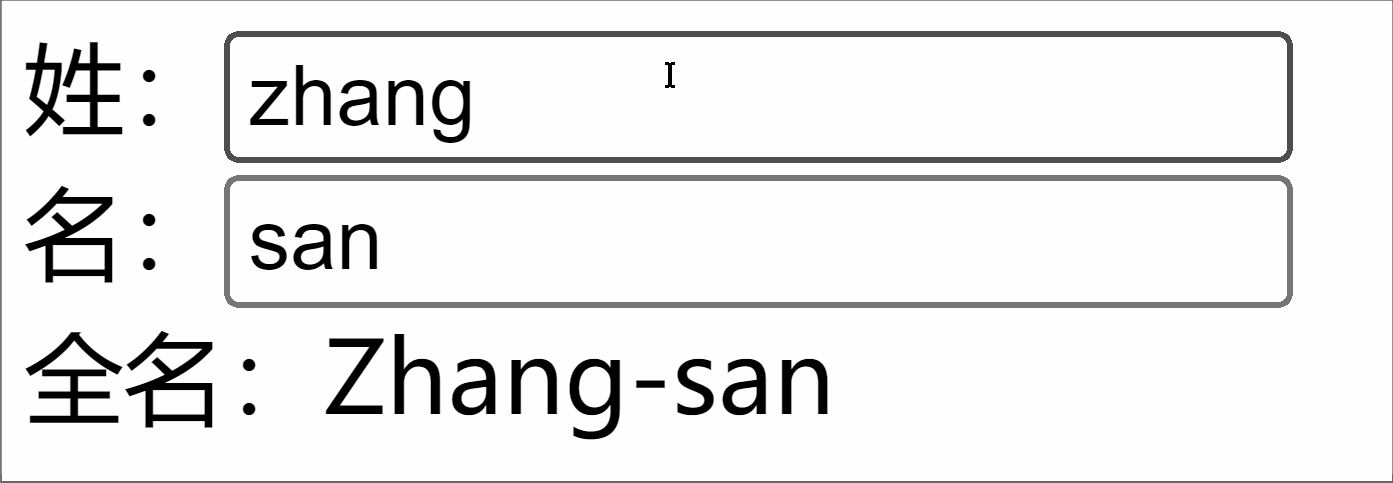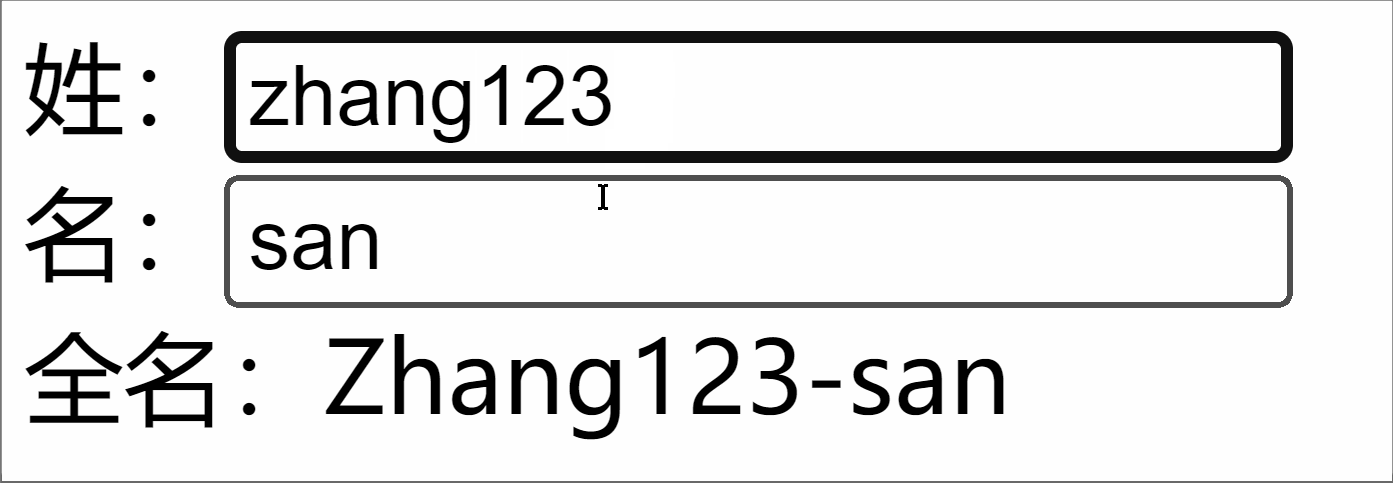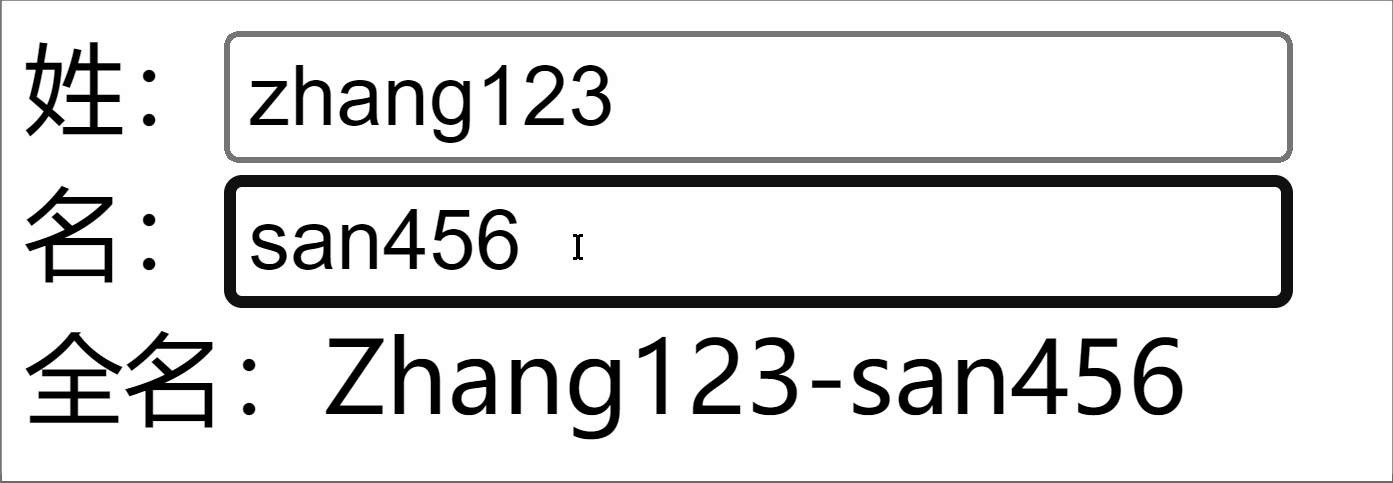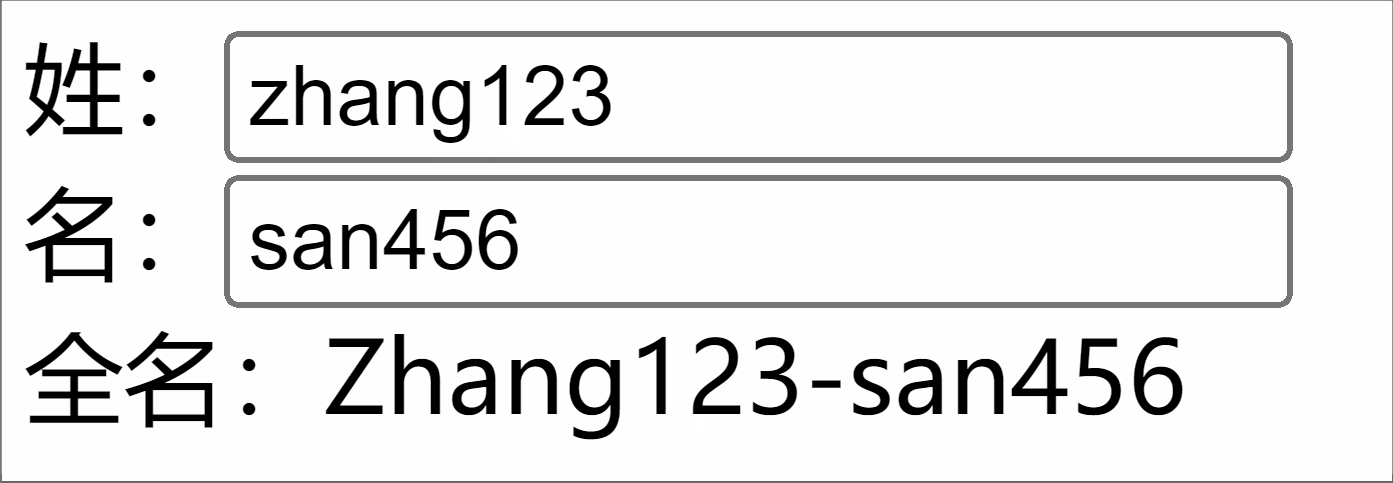
Vue3学习(4)- computed的使用
1. 简述与使用 作用:computed 用于基于响应式数据派生出新值,其值会自动缓存并在依赖变化时更新。 缓存机制:依赖未变化时直接返回缓存值,避免重复计算(通过 _dirty 标志位实现)。响应式更新&…...
手机上网可以固定ip地址吗?详细解析
在移动互联网时代,手机已成为人们日常上网的主要设备之一。无论是工作、学习还是娱乐,稳定的网络连接都至关重要。许多用户对IP地址的概念有所了解,尤其是固定IP地址的需求。那么,手机上网能否固定IP地址?又该如何实现…...

电脑同时连接内网和外网的方法,附外网连接局域网的操作设置
对于工作一般都设置在内网网段中,而同时由于需求需要连接外网,一般只能通过内网和外网的不断切换进行设置,如果可以同时连接内网和外网会更加便利,同时连接内网和外网方法具体如下。 一、电脑怎么弄可以同时连接内网和外网&#…...

如何在Unity中实现点击一个按钮跳转到哔哩哔哩
1.创建一个按钮 2.编写一个脚本(你可以把链接改成你想要跳转的网站) using System.Collections; using System.Collections.Generic; using UnityEngine; using UnityEngine.UI;public class JumpToBilibili : MonoBehaviour {void Start(){gameObject.…...
逐层封装过程: DHCP --> UDP --> IP)
DHCP 动态主机配置协议(Dynamic host configuration protocol)逐层封装过程: DHCP --> UDP --> IP
📦 DHCP 报文逐层封装结构(自上而下) 应用层(DHCP 报文) ↓ 传输层(UDP 首部) ↓ 网络层(IP 首部) ↓ 数据链路层(以太网帧头) ↓ 物理层&#x…...

PySide6 GUI 学习笔记——常用类及控件使用方法(单行文本控件QLineEdit)
文章目录 QLineEdit 介绍常用方法QLineEdit.EchoMode 取值光标相关方法文本选择方法输入格式化字符(Input Mask)常用信号QLineEdit 实例 QLineEdit 介绍 QLineEdit 是 PySide6(Qt for Python)中用于单行文本输入的控件。它支持文本…...

【数据结构】6. 时间与空间复杂度
文章目录 一、算法效率1、算法的复杂度 二、时间复杂度1、时间复杂度的概念2、大O的渐进表示法3、常见时间复杂度计算1)实例12)实例23)实例34)实例45)实例56)实例67)实例78)实例8 三…...
)
Python 函数全攻略:函数进阶(生成器、闭包、内置函数、装饰器、推导式)
一、默认参数中的易错点 问题: 当函数的默认参数是可变类型(如 list, dict)时,存在“坑”。 现象: def func(a2=[]): # a2 默认是一个空列表a2.append(2)print(a2)func() # 第一次调用,a2 默认为 [],输出 [2] func([]) # 传入新列表,输出 [2] func([1]) # 传入带元素的…...

基于springboot的藏文古籍系统
博主介绍:高级开发,从事互联网行业六年,熟悉各种主流语言,精通java、python、php、爬虫、web开发,已经做了多年的设计程序开发,开发过上千套设计程序,没有什么华丽的语言,只有实实在…...

重构城市应急指挥布控策略 ——无人机智能视频监控的破局之道
在突发事件、高空巡查、边远区域布控中,传统摄像头常常“看不到、跟不上、调不动”。无人机智能视频监控系统,打破地面视角局限,以“高空布控 AI分析 实时响应”赋能政企单位智能化管理。在城市应急指挥中心的大屏上,一场暴雨正…...

声音信号的基频检测(python版本)
import math import wave import array import functools from abc import ABC, abstractmethod import matplotlib import matplotlib.pyplot as plt from matplotlib.gridspec import GridSpec import os import sys# 设计模式部分 class PreprocessStrategy(ABC):"&q…...

STM32 控制12VRGB灯带颜色亮度调节,TFTLCD显示
接了一个同学的小项目,要实现控制一个实体,控制灯带的亮度为红/绿/蓝/白/黄以及亮度的叠加。 时间要的比较急,要两天实现,因此不能打板,只能采用现有模块拼接。 一. 实施方案 一开始觉得很简单,就是使用五…...
