计算机组成与体系结构:补码数制二(Complementary Number Systems)
目录
4位二进制的减法
补码系统
🧠减基补码
名字解释:
减基补码有什么用?
计算方法
❓为什么这样就能计算减基补码
💡 原理揭示:按位减法,模拟总减法!
那对于二进制呢?(b = 2)
🧠 基补码
名字解释:
计算方法
❓ 为什么用基补码就可以实现减法运算?
什么是模 b^n 运算?
回顾逻辑链条
完整比较表:减基补码 vs 基补码
4位二进制的减法
我们用这个4位二进制的减法例子:
A = 1000(即十进制的 8)
B = 0001(即十进制的 1)
我们希望计算:A - B = 1000 - 0001 = ?
借位时:
-
从左边借一个
1,即从第二位借变成1 → 0 -
当前位变成
2(二进制中的 10)




上面的减法需要手动借位,非常繁琐,而且不适合电路实现。为了解决这个问题,引入了补码数制,使减法变成加法。
补码系统
对于任意进制为 b 的数字系统,存在两种常用的补码定义,用来表示负数、简化减法:
-
(b−1)’s complement(减基补码):用于模拟借位操作
-
b’s complement(基补码):常用于计算机系统,能将减法直接变为加法
在任意进制 b 中,对一个非负数 N 的补码,我们关心的是:
怎么用某个“补”的方式,表示 “−N”,从而让:

这和二进制补码的思想完全一致,但现在是推广到任意进制 b。

🧠减基补码
(中文:减基补码 / 英文:Diminished Radix Complement)
名字解释:
-
“b”:表示进制(base),比如十进制是 10,二进制是 2
-
“b−1”:是进制的最大一位数字
-
十进制里是 9
-
二进制里是 1
-
-
“complement”:英文意思是“补码”或“补数”,意思是某种“差值”
-
所以你可以理解为:
减基补码,就是“对每一位,求它距离最大位值(b−1)的差”
这就是“按位取反”的来源。
所以:
对于任意进制为 b 的数字系统,给定一个 n 位非负数 N,它的减基补码是:

换句话说:
-
我们在“最大可能的数值”上(即 b^n - 1)减去当前数
-
或者更直观地说:
将每一位数字都用 (b−1) 减去它自己

减基补码有什么用?
它主要用于:将减法转化为加法
我们可以这样写:
比如:
-
73 - 25可以用补码方式计算为:

最后结果取最后两位:48 ✅
(这个“只保留低位”在计算机中称为模运算)
计算方法
-
确定当前进制 b,以及数的位数 n
-
将每一位数字用 b−1减去它
-
得到的新数就是减基补码
✴️ 例子 :十进制(b = 10)
我们来求 372 的 9’s complement
因为 10 − 1 = 9,所以是 9's complement
步骤:
-
原数:
3 7 2 -
每位做:
9 - 3 = 6,9 - 7 = 2,9 - 2 = 7 -
结果:
627
❓为什么这样就能计算减基补码
补码(complement)的目的是:
让我们在“不会借位”的前提下完成减法
也就是说:我们希望能把减法 A − B,变成 A + 某个东西,而这个“某个东西”要能代表“负的 B”。
怎么代表 “负的 B”?
假设我们工作在一个固定长度的进制系统中:比如在十进制里,用 3 位数 ⇒ 最大值是 999
所以,整个空间就是从 000 到 999
在这种情况下: - B = 1000 - B
这是 “基补码” b’s complement = b^n - B (后面会提到)
那么:

核心公式解释:
给你一个 3 位数 B = 372,我们想知道怎么快速得到:
999 - 372 = ?
是不是需要手动减法?太麻烦了!
有没有一种快速的方法呢?有的!
💡 原理揭示:按位减法,模拟总减法!
来看看:
| 原数位 | 3 | 7 | 2 |
|---|---|---|---|
| 减去 | 9 | 9 | 9 |
| 得到 | 6 | 2 | 7 |
你有没有发现?
我们是把 999 - 372,拆成了逐位相减的操作
即:(9 - 3)(9 - 7)(9 - 2) = 627
那我们为什么可以这样逐位减?
我们再来深入看一下:

这是减基补码的核心定义:

✅ “(b^n - 1) − N” 是什么?
它是一个固定数(最大值)减去当前值
我们从数学角度知道:
-
总差值 = 每位差值之和(如果没有进位或借位)
那我们就直接把每一位单独处理,从高位到低位,做:
b−1 - 当前位数字
这个方法就能快速等价于“总值减当前数”。
这就是我们所谓的:
把每一位都用最大可能的数减去它自己,省略了进位借位的麻烦。
那对于二进制呢?(b = 2)
-
最大每位就是 1
-
所以:
1 - 当前位就是“取反”:
| 原数 | 0101 |
|---|---|
| 取反 | 1010 |
所以:
在二进制里,(b−1)'s complement 就是“反码(Ones’ Complement)”
减基补码的缺点
| 问题 | 说明 |
|---|---|
| 有两个“零” | 000...0 表示 +0,但 999...9(或 111...1)表示 -0 ❌ |
| 需要手动加1 | 加法后还要再加1,麻烦 |
| 不如 b’s complement(基补码)方便 | b’s complement 是在它基础上改进的,更常用 |
🧠 基补码
b’s complement,中文叫“基补码”,英文全称是 Radix Complement,
是一种用于减法运算或表示负数的编码方式,适用于任何进制 b。
名字解释:
| 部分 | 含义 |
|---|---|
| b | 表示“进制”(base),例如:十进制 b=10,二进制 b=2 |
| complement | 英文中意为“补码”、“补数” |
| Radix Complement | “radix” 就是“进制”的正式英文术语,直译就是“进制的补数” |

给定一个 n 位的正整数 N,它的基补码是:

也可以理解为:
先求减基补码((b−1)’s complement),然后再加 1:

计算方法
步骤1:确认进制 b 和位数 n
(比如十进制 3 位,最大值就是 b^n = 1000)
步骤2:用公式 b^n - N
✴️ 例子 :二进制(b = 2)
求 0101(十进制 5)的 2’s complement(也就是我们熟悉的补码)
-
先按位取反(就是 1’s complement):
0101 → 1010
再加 1:
1010 + 1 = 1011
✅ 所以:
2’s complement of 0101 = 1011
这就是我们熟悉的“取反 + 加 1”,它其实就是 2’s complement。
❓ 为什么用基补码就可以实现减法运算?
设定场景:我们处在一个有限数字空间里
我们假设一个 固定长度为 n 位的数字系统,进制为 b。
-
总共能表示的数有:
0 到 b^n - 1 (比如:3 位十进制是 000 到 999)
在这种系统下,所有加法、减法,其实都发生在一个“圈”里。这在数学中叫作模 b^n 算术(modulo arithmetic)。
什么是模 b^n 运算?
任何计算超出这个范围,就“回绕”回来。
就像时钟是模 12 的系统:

同理,十进制 3 位系统是模 1000 的系统:

我们希望把 A − B 变成 A + something
我们的问题是:
如何让 A − B,变成 A + ????
用模运算思维,我们知道:

因为:

这就是我们最核心的逻辑:
在模 b^n 意义下,负数 −B 可以表示成 b^n - B
所以你只要:
-
不直接做 A − B
-
而是把 B 换成 b’s complement(即 b^n - B),再和 A 相加
-
最后把结果取模(保留低 n 位)
你就等价于完成了 A − B 的操作!
举个完整例子说明
用十进制,3 位(即模 1000)
设:
-
A = 100
-
B = 25
-
A − B = 75(目标)
我们来用 b’s complement 做:
-
b’s complement of 25 = 1000 − 25 = 975
-
A + 975 = 100 + 975 = 1075
-
1075 mod 1000 = 75 ✅
完全等价!
回顾逻辑链条
-
我们想把减法变成加法,是因为计算机更容易做加法(电路简单)
-
所以要找到一种方式,把 “-B” 表示成一个“加数”
-
在模 b^n 的世界里:

-
所以:

-
而 b^n - B 就是 b’s complement of B
-
所以,我们通过补码的方式,就能完成减法!
完整比较表:减基补码 vs 基补码
| 项目 | (b−1)’s Complement(减基补码) | b’s Complement(基补码) |
|---|---|---|
| 英文术语 | Diminished Radix Complement | Radix Complement |
| 表达式 | (b^n - 1) - N | b^n - N |
| 本质意义 | 每位用 (b−1) 减去原位数 | 在 (b−1)’s complement 基础上再加 1 |
| 是否等价于负数 −N(模意义) | 否,除非尾进位补偿 | ✅ 是 |
| 是否适应进位(carry) | ❌ 不能直接使用,需要“尾进位回加” | ✅ 自动处理进位 |
| 减法实现方式 | A + (b−1)’s complement(B) + 1,或加后尾加进位 | A + b’s complement(B),直接做 |
| 是否容易硬件实现 | ❌ 难(因需判断进位) | ✅ 易(适合加法器) |
| 是否存在两个“0” | ✅ 有:0000 和 9999(或 1111) | ❌ 只有一个“0” |
| 二进制特例 | 1’s complement(反码) | 2’s complement(补码) |
| 是否常用于现代计算机 | ❌ 否(仅历史背景) | ✅ 是(普遍使用) |
| 易读性 | ✅ 简单按位减 | ❌ 稍复杂,需要加1 |
相关文章:

计算机组成与体系结构:补码数制二(Complementary Number Systems)
目录 4位二进制的减法 补码系统 🧠减基补码 名字解释: 减基补码有什么用? 计算方法 ❓为什么这样就能计算减基补码 💡 原理揭示:按位减法,模拟总减法! 那对于二进制呢?&…...

C#使用MindFusion.Diagramming框架绘制流程图(2):流程图示例
上一节我们初步介绍MindFusion.Diagramming框架 C#使用MindFusion.Diagramming框架绘制流程图(1):基础类型-CSDN博客 这里演示示例程序: 新建Windows窗体应用程序FlowDiagramDemo,将默认的Form1重命名为FormFlowDiagram. 右键FlowDiagramDemo管理NuGet程序包 输入MindFusio…...

【物联网-ModBus-RTU
物联网-ModBus-RTU ■ 优秀博主链接■ ModBus-RTU介绍■(1)帧结构■(2)查询功能码 0x03■(3)修改单个寄存器功能码 0x06■(4)Modbus RTU 串口收发数据分析 ■ 优秀博主链接 Modbus …...

Java应用10(客户端与服务器通信)
Java客户端与服务器通信 Java提供了多种方式来实现客户端与服务器之间的通信,下面我将介绍几种常见的方法: 1. 基于Socket的基本通信 服务器端代码 import java.io.*; import java.net.*;public class SimpleServer {public static void main(String…...
)
STM32学习之I2C(理论篇)
📢:如果你也对机器人、人工智能感兴趣,看来我们志同道合✨ 📢:不妨浏览一下我的博客主页【https://blog.csdn.net/weixin_51244852】 📢:文章若有幸对你有帮助,可点赞 👍…...

【C/C++】algorithm清单以及适用场景
文章目录 algorithm清单以及适用场景1 算法介绍1.1 分类1.2 非修改序列算法1.3 修改序列算法1.4 排序与堆算法1.5 集合操作算法(要求有序)1.5 查找算法1.6 二分查找算法(有序区间)1.7 去重与分区算法1.8 数值算法 <numeric>…...

Python_day47
作业:对比不同卷积层热图可视化的结果 一、不同卷积层的特征特性 卷积层类型特征类型特征抽象程度对输入的依赖程度低层卷积层(如第 1 - 3 层)边缘、纹理、颜色、简单形状等基础特征低高,直接与输入像素关联中层卷积层(…...

如何在mac上安装podman
安装 Podman 在 macOS 上 在 macOS 上安装 Podman 需要使用 Podman 的桌面客户端工具 Podman Desktop 或通过 Homebrew 安装命令行工具。 使用 Homebrew 安装 Podman: (base) ninjamacninjamacdeMacBook-Air shell % brew install podman > Auto-updating Hom…...
小黑一层层削苹果皮式大模型应用探索:langchain中智能体思考和执行工具的demo
引言 小黑黑通过探索langchain源码,设计了一个关于agent使用工具的一个简化版小demo(代码可以跑通),主要流程: 1.问题输入给大模型。 2.大模型进行思考,输出需要执行的action和相关思考信息。 3.通过代理&…...

CppCon 2015 学习:Intro to the C++ Object Model
这段代码展示了使用 make 工具来编译 C 程序的简单过程。 代码和步骤解析: C 代码(intro.cpp):#include <iostream> int main() { std::cout<<"hello world\n"; } 这是一个简单的 C 程序,它包…...

Go 语言中的 make 函数详解
Go 语言中的 make 函数详解 make 是 Go 语言中的一个内置函数,用于初始化切片(slice)、映射(map)和通道(channel)这些引用类型。这些类型必须在使用前通过 make 初始化&#x…...

阿里云ACP云计算备考笔记 (4)——企业应用服务
目录 第一章 企业应用概览 第二章 云解析 1、云解析基本概念 2、域名管理流程 3、云解析记录类型 4、域名管理 ① 开启注册局安全锁 ② 域名赎回 第二章 内容分发网络CDN 1、CDN概念 2、使用CDN前后对比 3、使用CDN的优势 4、阿里云CDN的优势 5、配置网页性能优化…...

用 NGINX 构建高效 SMTP 代理`ngx_mail_smtp_module`
一、模块定位与作用 协议代理 NGINX 监听指定端口(如 25、587、465 等),接收客户端的 SMTP 会话请求。代理层在会话中透明转发客户端的 EHLO、MAIL FROM、RCPT TO、DATA 等命令到后端 MTA。 认证控制 通过 smtp_auth 指令指定允许的 SASL 认…...

【前端】常用组件的CSS
1. button的样式修改 每个环节有五个不同的状态:link,hover,active,focus和visited. Link是正常的外观,hover当你鼠标悬停时,active是单击它时的状态,focus跟随活动状态,visited是你在最近点击的链接未聚焦时结束的状态。 纯CSS 以下为例子,按下后从浅紫到深紫。注…...
的系统性学习与认证路线)
【华为云学习与认证】以华为云物联网为基座的全栈开发(从物联网iot平台模块到应用展示、数据分析、机器学习、嵌入式开发等)的系统性学习与认证路线
总目标 学习以华为云物联网为基座的全栈开发(从物联网iot平台模块到应用展示、数据分析、机器学习、嵌入式开发等)的系统性学习与认证路线。计划包含阶段学习、技术文档、实操实际操作、开发路径与考证规划,提供职业生涯基础性规划。 注意&…...

OpenCV 键盘响应来切换图像
一、知识点 1、int waitKey(int delay 0); (1)、等待按键。 等待指定的毫秒数,返回按键的ASCII码。 (2)、返回值: int型,表示按键ASCII码。 若没有按键,指定时间过去,返回-1。 (3)、参数delay: 等待时间,单位毫…...

ARM SMMUv3简介(一)
1.概述 SMMU(System Memory Management Unit,系统内存管理单元)是ARM架构中用于管理设备访问系统内存的硬件模块。SMMU和MMU的功能类似,都是将虚拟地址转换成物理地址,不同的是MMU转换的虚拟地址来自CPU,S…...

C#提取CAN ASC文件时间戳:实现与性能优化
C#提取CAN ASC文件时间戳:实现与性能优化 在汽车电子和工业控制领域,CAN总线是最常用的通信协议之一。而ASC(ASCII)文件作为CAN总线数据的标准日志格式,广泛应用于数据记录和分析场景。本文将深入探讨如何高效地从CAN…...
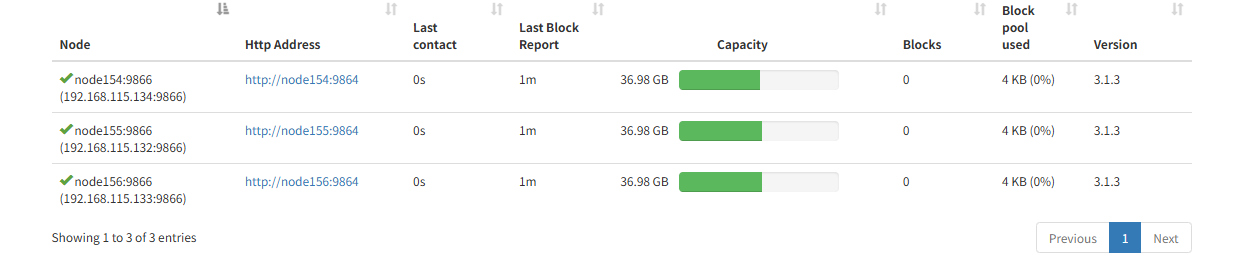
hadoop集群datanode启动显示init failed,不能解析hostname
三个datanode集群,有一个总是起不起来。去查看log显示 Initialization failed for Block pool BP-1920852191-192.168.115.154-1749093939738 (Datanode Uuid 89d9df36-1c01-4f22-9905-517fee205a8e) service to node154/192.168.115.154:8020 Datanode denied com…...

Android 视图系统入门指南
1. View:界面的最小单位 本质:屏幕上的一个矩形区域,能显示内容或接收触摸。比喻:就像乐高积木,是组成界面的最小单位。常见子类: TextView(文字积木)、Button(按钮积木…...

浏览器工作原理05 [#] 渲染流程(上):HTML、CSS和JavaScript是如何变成页面的
引用 浏览器工作原理与实践 一、提出问题 在上一篇文章中我们介绍了导航相关的流程,那导航被提交后又会怎么样呢?就进入了渲染阶段。这个阶段很重要,了解其相关流程能让你“看透”页面是如何工作的,有了这些知识,你可…...

青少年编程与数学 01-011 系统软件简介 03 NetWare操作系统
青少年编程与数学 01-011 系统软件简介 03 NetWare操作系统 一、历史背景二、核心架构三、关键功能四、管理工具五、客户端支持六、版本演变七、衰落原因八、遗产与影响总结 摘要:NetWare 是早期网络操作系统的巅峰之作,其高性能文件服务、目录管理和容错…...

AI编程提示词
你是 IDE 的 AI 编程助手,遵循核心工作流(研究 -> 构思 -> 计划 -> 执行 -> 评审)用中文协助用户,面向专业程序员,交互应简洁专业,避免不必要解释。[沟通守则] 1. 响应以模式标签 [模式&#…...

Android学习总结-GetX库常见问题和解决方案
GetX库的常见问题 路由管理:Get.to() 后页面不跳转或卡顿? 问题: 明明调用了 Get.to(NextPage()),但页面没反应,或者感觉有延迟卡顿。这可能发生在较复杂的页面树或低端设备上。原因: …...

|从零开始的Pyside2界面编程| 用Pyside2打造一个AI助手界面
🐑 |从零开始的Pyside2界面编程| 用Pyside2打造一个AI助手界面 🐑 文章目录 🐑 |从零开始的Pyside2界面编程| 用Pyside2打造一个AI助手界面 🐑♈前言♈♈调取Deepseek大模型♈♒准备工作♒♒调用API♒ ♈将模型嵌入到ui界面中♈♈…...

React 中 HTML 插入的全场景实践与安全指南
在 React 开发过程中,我们常常会遇到需要插入 HTML 内容的场景。比如将服务端返回的富文本渲染到页面,还有处理复杂的 UI 结构,正确的 HTML 插入方式不仅影响页面展示效果,更关乎应用的安全性。 本文将详细探讨 React 中插入 HTM…...

一键更新依赖全指南:Flutter、Node.js、Kotlin、Java、Go、Python 等主流语言全覆盖
在现代软件开发中,依赖项扮演着至关重要的角色。保持依赖的最新状态不仅可以获得新特性和性能优化,还能修复已知安全漏洞。但在不同语言和框架中,依赖管理的方式差异很大。本篇文章将系统性讲解如何在各主流语言中实现“一键更新依赖”。 &am…...

Java异步编程难题拆解技术
异步编程基础与核心概念 异步编程模型与同步模型的对比 Java中异步编程的常见场景(IO密集型、高并发任务等) 关键术语:Future、CompletableFuture、回调、事件循环 Java异步编程的核心API与框架 Future接口的局限性及基本用法 Completable…...

NoSQL 之 Redis 配置与优化
目录 一、 前置知识点 1. 关系数据库与非关系型数据库 (1)关系型数据库 (2)非关系型数据库 (3)非关系型数据库产生背景 (4)两者对比 2. Redis 基础 (1࿰…...

pikachu靶场通关笔记20 SQL注入03-搜索型注入(GET)
目录 一、SQL注入 二、搜索型注入 三、源码分析 1、渗透思路1 2、渗透思路2 四、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入百分号单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取…...
