当前位置： 首页 > article >正文

virtualbox 如何虚拟机ip固定

article 2025/6/9 17:48:22

1、在网络管理里新建

在这里插入图片描述

2、配置网络

在这里插入图片描述

在这里插入图片描述

3、 进入linux系统，查看

查看 网卡是enp0s8,

ifconfig

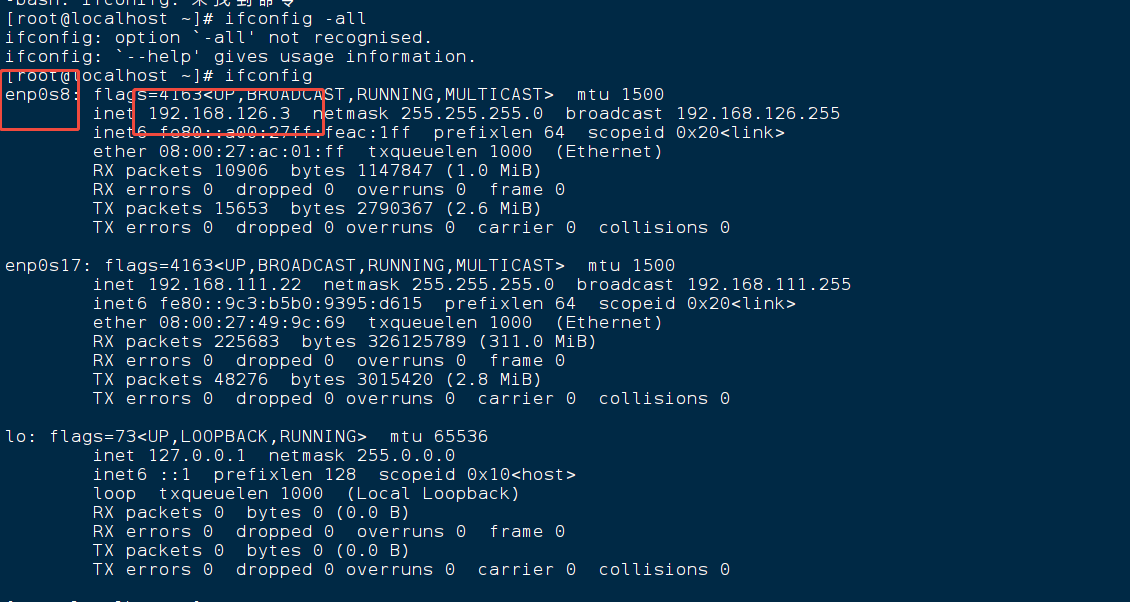
在这里插入图片描述

4、进入网卡配置文件

cd  /etc/sysconfig/network-scripts

在这里插入图片描述

如果没有enp0s8 ，则使用mv ifcfg-enp0s3 ifcfg-enp0s8命令
配置项如下

TYPE=Ethernet
PROXY_METHOD=none
BROWSER_ONLY=no
BOOTPROTO=static
DEFROUTE=yes
IPV4_FAILURE_FATAL=no
IPV6INIT=no
IPV6_AUTOCONF=yes
IPV6_DEFROUTE=yes
IPV6_FAILURE_FATAL=no
IPV6_ADDR_GEN_MODE=stable-privacy
NAME=enp0s8
UUID=d97d3c43-c454-4dc0-86f3-146ae9355545
DEVICE=enp0s8
ONBOOT=yes
IPADDR=192.168.126.3

主要修改这三个文件，把ipv6设置为no IPV6INIT=no

在这里插入图片描述

5、重启网络

systemctl restart network

相关文章：

virtualbox 如何虚拟机ip固定

1、在网络管理里新建 2、配置网络 3、 进入linux系统，查看 查看 网卡是enp0s8, ifconfig 4、进入网卡配置文件 cd /etc/sysconfig/network-scripts如果没有enp0s8 ，则使用mv ifcfg-enp0s3 ifcfg-enp0s8命令 配置项如下 TYPEEthernet PROXY_METHODn…...

编程日记 2025/6/9 17:48:22

RKNN3588上部署 RTDETRV2

RT-DETR V2 是由百度研究团队在 2024年 提出的，是其广受好评的实时目标检测模型 RT-DETR 的重大升级版本。它继承了第一代 RT-DETR 利用 Transformer 架构实现端到端目标检测 和 卓越实时性能 的核心优势，并针对模型精度、训练效率和部署灵活性进行了全方…...

编程日记 2025/6/9 17:47:20

Python----循环神经网络（BiLSTM：双向长短时记忆网络）

一、LSTM 与 BiLSTM对比 1.1、LSTM LSTM（长短期记忆网络） 是一种改进的循环神经网络（RNN），专门解决传统RNN难以学习长期依赖的问题。它通过遗忘门、输入门和输出门来控制信息的流动，保留重要信息并丢弃无关…...

编程日记 2025/6/9 17:45:16

Elasticsearch 常用操作命令整合 (cURL 版本)

Elasticsearch 常用操作命令整合 (cURL 版本) 集群管理 查看集群健康状态 curl -X GET "localhost:9200/_cluster/health?pretty"查看节点信息 curl -X GET "localhost:9200/_cat/nodes?v"查看集群统计信息 curl -X GET "localhost:9200/_clus…...

编程日记 2025/6/9 17:44:13

Redis持久化策略：RDB与AOF详解

目录 1. RDB持久化工作原理触发机制优点缺点配置示例 2. AOF持久化工作原理同步策略重写机制优点缺点配置示例 3. RDB与AOF比较4. 混合持久化(Redis 4.0)5. 选择建议 Redis提供了两种主要的持久化机制来保证数据安全：RDB(Redis Database)和AOF(Append Only File)。本…...

编程日记 2025/6/9 17:43:11

Linux系统编程-DAY10（TCP操作）

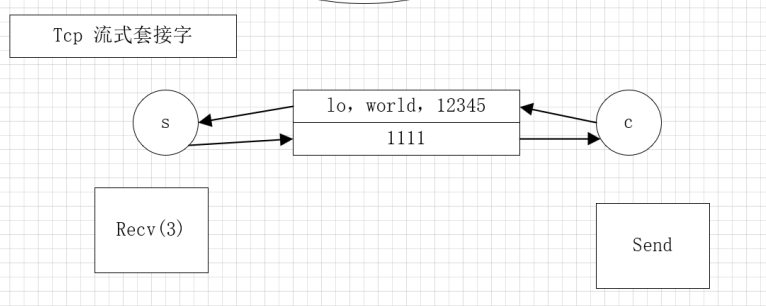
一、网络模型 1、服务器/客户端模型 （1）C/S：client server （2）B/S：browser server （3）P2P：peer to peer 2、C/S与B/S区别 （1）客户端不同&#…...

编程日记 2025/6/9 17:42:09

基于eclipse进行Birt报表开发

Birt报表开发最终实现效果： 简洁版的Birt报表开发实现效果，仅供参考！ 可动态获取采购单ID，来打印出报表！ 下面开始Birt报表开发教程： 首先：汉化的eclipse及Birt值得拥有：至少感觉上…...

编程日记 2025/6/9 17:41:07

GPU虚拟化

引言 现有如下环境（注意相关配置：只有一个k8s节点，且该节点上只有一张GPU卡）： // k8s版本 $ kubectl version Client Version: version.Info{Major:"1", Minor:"22", GitVersion:"v1.22.7&…...

编程日记 2025/6/9 17:40:05

LabVIEW工业级多任务实时测控系统

采用LabVIEW构建了一套适用于工业自动化领域的多任务实时测控系统。系统采用分布式架构，集成高精度数据采集、实时控制、网络通信及远程监控等功能，通过硬件与软件的深度协同，实现对工业现场多类型信号的精准测控，展现 LabVIEW 在…...

编程日记 2025/6/9 17:39:03

Python学习(7) ----- Python起源

🐍《Python 的诞生》：一段圣诞假期的奇妙冒险 📍时间：1989 年圣诞节 在荷兰阿姆斯特丹的一个寒冷冬夜，灯光昏黄、窗外飘着雪。一个程序员 Guido van Rossum 正窝在家里度假——没有会议、没有项目、没有 bug&#xf…...

编程日记 2025/6/9 17:38:00

Java中List的forEach用法详解

在 Java 中，List.forEach() 是 Java 8 引入的一种简洁的遍历集合元素的方法。它基于函数式编程思想，接受一个 Consumer 函数式接口作为参数，用于对集合中的每个元素执行操作。 基本语法 java 复制 下载 list.forEach(consumer); 使用示…...

编程日记 2025/6/9 17:36:58

LeetCode 1356.根据数字二进制下1的数目排序

题目&#xff1a; 给你一个整数数组 arr 。请你将数组中的元素按照其二进制表示中数字 1 的数目升序排序。 如果存在多个数字二进制中 1 的数目相同&#xff0c;则必须将它们按照数值大小升序排列。 请你返回排序后的数组。 提示&#xff1a; 1 < arr.length < 5000…...

编程日记 2025/6/9 17:35:50

破解HTTP无状态：基于Java的Session与Cookie协同工作指南

HTTP协议自身是属于“无状态”协议 无状态是指&#xff1a;默认情况下&#xff0c;HTTP协议的客户端和服务器之间的这次通信&#xff0c;和下次通信之间没有直接的关系 但在实际开发中&#xff0c;我们很多时候是需要知道请求之间的关联关系的 上述图中的令牌&#xff0c;通常就…...

编程日记 2025/6/9 17:34:43

JS 事件流机制详解：冒泡、捕获与完整事件流

JS 事件流机制详解&#xff1a;冒泡、捕获与完整事件流 文章目录 JS 事件流机制详解&#xff1a;冒泡、捕获与完整事件流一、DOM 事件流基本概念二、事件捕获 (Event Capturing)特点代码示例 三、事件冒泡 (Event Bubbling)特点代码示例 四、完整事件流示例HTML 结构JavaScript…...

编程日记 2025/6/9 17:33:31

MYSQL too many connection问题排查和修复

1.连接数据库 mysql -u root -p 1.1 查看mysql路径 如果没有配置mysql的环境变量&#xff0c;可以直接找mysql的安装目录 打开任务管理器-》服务-》Mysql(根据版本不同后面带有数字&#xff0c;找运行的那个) 打开服务->mysql->属性-》可执行文件的路径&#xff0c;…...

编程日记 2025/6/9 17:32:25

SpringCloudAlibaba和SpringBoot版本问题

SpringCloudAlibaba和SpringBoot版本问题 直接参考官方给出的版本说明&#xff0c;具体地址&#xff1a;https://github.com/alibaba/spring-cloud-alibaba/wiki/%E7%89%88%E6%9C%AC%E8%AF%B4%E6%98%8E Spring Cloud Alibaba VersionSentinel VersionNacos VersionRocketMQ Ver…...

编程日记 2025/6/9 17:31:20

算法专题七：分治

快排 1.颜色分类 题目链接：75. 颜色分类 - 力扣（LeetCode） class Solution {public void swap(int[] nums, int i, int j){int t = nums[i];nums[i] = nums[j];nums[j] = t;}public void sortColors(int[] nums) {int left=-1 ,i=0 ,right=nums.length;while(i<right){i…...

编程日记 2025/6/9 17:30:19

Vue中虚拟DOM的原理与作用

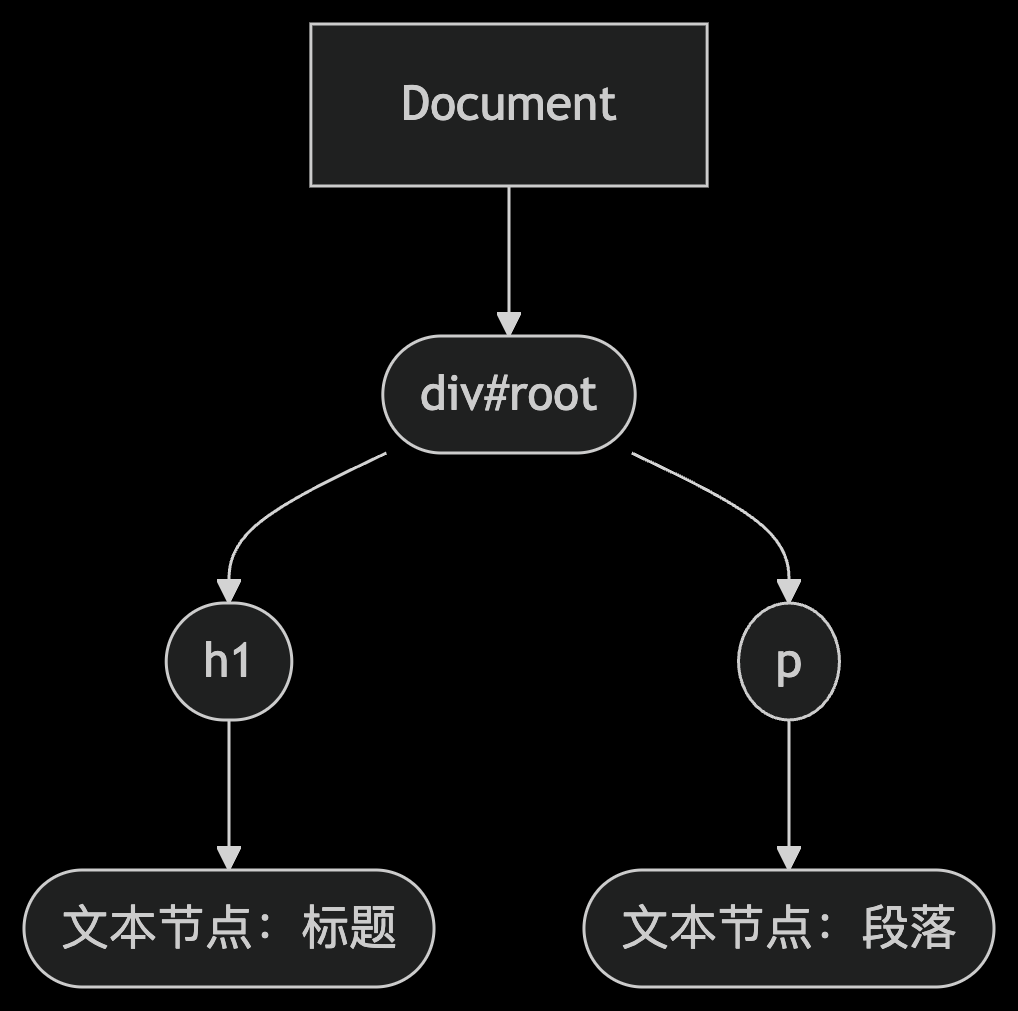
绪论 首先我们先了解&#xff0c;DOM&#xff08;Document Object Model&#xff0c;文档对象模型&#xff09; 是浏览器对 HTML/XML 文档的结构化表示&#xff0c;它将文档解析为一个由节点&#xff08;Node&#xff09;和对象组成的树形结构&#xff08;称为 DOM 树&#xf…...

编程日记 2025/6/9 17:29:17

前端十种排序算法解析

1. 冒泡排序 1.1 说明 冒泡排序为一种常用排序算法&#xff0c;执行过程为从数组的第一个位置开始&#xff0c;相邻的进行比较&#xff0c;将最大的数移动到数组的最后位置执行的时间复杂度与空间复杂度为 o(n^2) 1.2 执行过程 从数组的第一个位置开始&#xff0c;截止位置为 …...

编程日记 2025/6/9 17:28:13

使用 C/C++ 和 OpenCV 添加图片水印

使用 C/C 和 OpenCV 添加图片水印 &#x1f5bc;️ 在数字图像处理中&#xff0c;添加水印是一种常见的操作&#xff0c;可以用于版权保护、品牌宣传或信息标注。本文将介绍如何使用 C/C 和强大的计算机视觉库 OpenCV 来实现将自定义水印&#xff08;图片或文字&#xff09;添…...

编程日记 2025/6/9 17:27:11

Secs/Gem第十二讲(基于secs4net项目的ChatGpt介绍)

好&#xff0c;那我们进入最关键的一讲—— 第十二讲&#xff1a;完整事件通知流程全景图——CEID 触发到主机接收的全过程 关键词&#xff1a;CEID 事件上报、S6F11 报文、事件触发流程、数据驱动机制、Report Dispatch、主机解析流程 本讲目标 你将彻底理解&#xff1a; 设…...

编程日记 2025/6/9 17:26:09

FastAPI实战起步：从Python环境到你的第一个“Hello World”API接口

上一篇文章中介绍了有关FastAPI的优势&#xff0c;本篇文章我将手把手带你从零开始&#xff0c;搭建FastAPI的开发环境&#xff0c;并成功运行你的第一个“Hello World”API。在开始之前&#xff0c;请确保你的电脑已经安装了Python 3.7或更高版本&#xff0c;以及VS Code&…...

编程日记 2025/6/9 17:25:07

使用vue3+ts+input封装上传组件，上传文件显示文件图标

效果图&#xff1a; 代码 <template><div class"custom-file-upload"><div class"upload"><!-- 显示已选择的文件 --><div class"file-list"><div v-for"(item, index) in state.filsList" :key&q…...

编程日记 2025/6/9 17:24:06

iOS 抖音导航栏首页一键分两列功能的实现

要实现 iOS 抖音首页导航栏的“一键分两列”功能&#xff08;通常指将单列内容切换为双列瀑布流布局&#xff09;&#xff0c;需结合自定义导航栏控件与布局动态切换逻辑。以下是关键实现步骤和技术要点&#xff0c;基于 iOS 原生开发框架&#xff08;Swift/Objective-C&#x…...

编程日记 2025/6/9 17:23:04

零基础入门 C 语言基础知识（含面试题）：结构体、联合体、枚举、链表、环形队列、指针全解析！

&#x1f31f; 零基础入门 C 语言基础知识&#xff08;含面试题&#xff09;&#xff1a;结构体、联合体、枚举、链表、环形队列、指针全解析&#xff01; C 语言是所有程序员通向“系统世界”的第一把钥匙。很多嵌入式开发、操作系统内核、网络通信、图形引擎&#xff0c;背后…...

编程日记 2025/6/9 17:22:02

【Linux】Ubuntu 创建应用图标的方式汇总，deb/appimage/通用方法

Ubuntu 创建应用图标的方式汇总&#xff0c;deb/appimage/通用方法 对于标准的 Ubuntu&#xff08;使用 GNOME 桌面&#xff09;&#xff0c;desktop 后缀的桌面图标文件主要保存在以下三个路径&#xff1a; 当前用户的桌面目录&#xff08;这是最常见的位置&#xff09;。所…...

编程日记 2025/6/9 17:21:01

【Unity】R3 CSharp 响应式编程 - 使用篇（集合）（三）

1、ObservableList 基础 List 类型测试 using System;using System.Collections.Specialized;using ObservableCollections;using UnityEngine;namespace Aladdin.Standard.Observable.Collections.List{public class ObservableListTest : MonoBehaviour{protected readonly O…...

编程日记 2025/6/9 17:19:55

振动力学：弹性杆的纵向振动（固有振动和固有频率的概念）

文章1、2、3中讨论的是离散系统的振动特性，然而实际系统的惯性质量、弹性、阻尼等特性都是连续分布的，因而成为连续系统或分布参数系统。确定连续介质中无数个点的运动需要无限个广义坐标，因此也称为无限自由度系统，典型的结构例如：弦、杆、膜、环、梁、板、壳等，也称为弹…...

编程日记 2025/6/9 17:18:54

LangGraph--Agent工作流

Agent的工作流 下面展示了如何创建一个“计划并执行”风格的代理。 这在很大程度上借鉴了 计划和解决 论文以及Baby-AGI项目。 核心思想是先制定一个多步骤计划&#xff0c;然后逐项执行。完成一项特定任务后&#xff0c;您可以重新审视计划并根据需要进行修改。 般的计算图如…...

编程日记 2025/6/9 17:17:51

Spring Boot 常用注解面试题深度解析

&#x1f91f;致敬读者 &#x1f7e9;感谢阅读&#x1f7e6;笑口常开&#x1f7ea;生日快乐⬛早点睡觉 &#x1f4d8;博主相关 &#x1f7e7;博主信息&#x1f7e8;博客首页&#x1f7eb;专栏推荐&#x1f7e5;活动信息 文章目录 Spring Boot 常用注解面试题深度解析一、核心…...

编程日记 2025/6/9 17:16:49